2020年绵阳市中考数学考点训练2：锐角三角函数（含答案） 12页

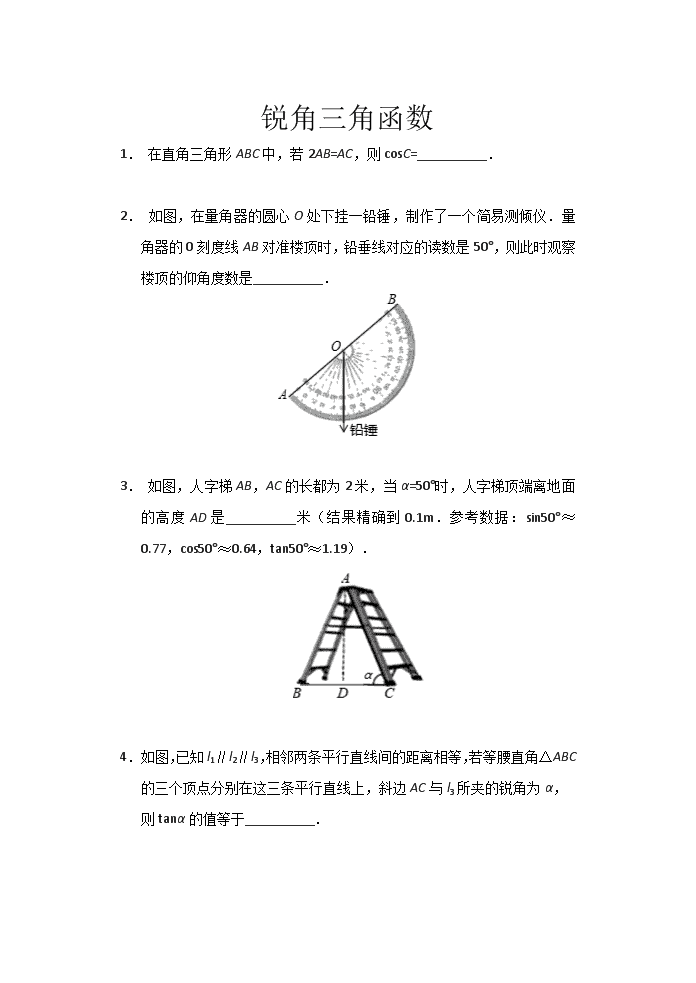
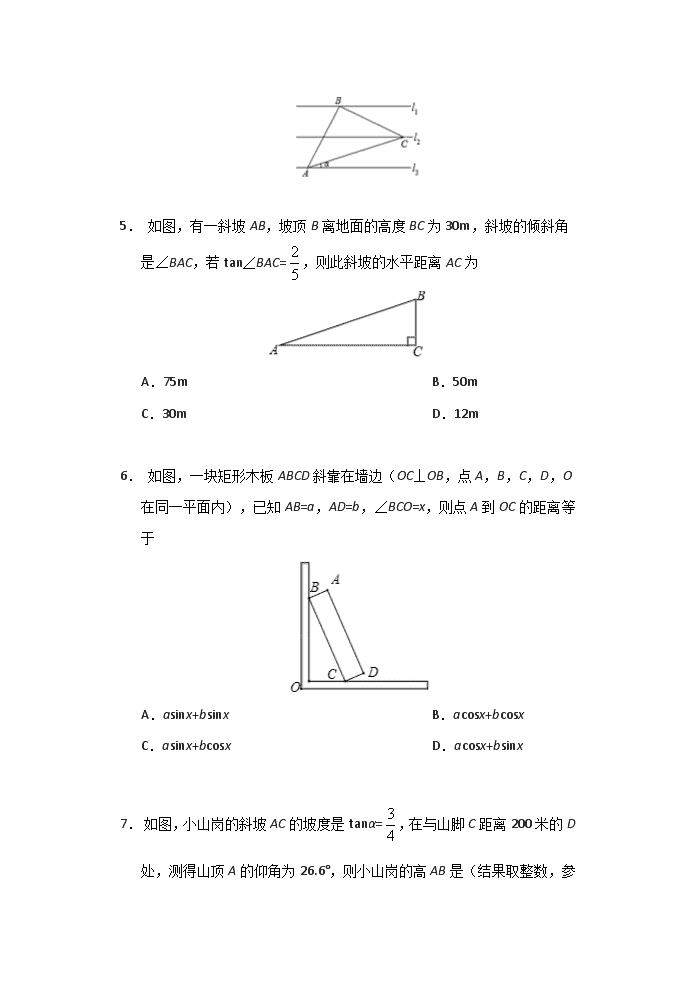
锐角三角函数 ‎1． 在直角三角形ABC中，若2AB=AC，则cosC=__________．‎ ‎ ‎ ‎2． 如图，在量角器的圆心O处下挂一铅锤，制作了一个简易测倾仪．量角器的0刻度线AB对准楼顶时，铅垂线对应的读数是50°，则此时观察楼顶的仰角度数是__________．‎ ‎ ‎ ‎3． 如图，人字梯AB，AC的长都为2米，当α=50°时，人字梯顶端离地面的高度AD是__________米（结果精确到0.1m．参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.19）．‎ ‎ ‎ ‎4． 如图，已知l1∥l2∥l3，相邻两条平行直线间的距离相等，若等腰直角△ABC的三个顶点分别在这三条平行直线上，斜边AC与l3所夹的锐角为α，则tanα的值等于__________．‎ ‎ ‎ ‎5． 如图，有一斜坡AB，坡顶B离地面的高度BC为30m，斜坡的倾斜角是∠BAC，若tan∠BAC=，则此斜坡的水平距离AC为 A．75m B．50m ‎ C．30m D．12m ‎ ‎ ‎6． 如图，一块矩形木板ABCD斜靠在墙边（OC⊥OB，点A，B，C，D，O在同一平面内），已知AB=a，AD=b，∠BCO=x，则点A到OC的距离等于 A．asinx+bsinx B．acosx+bcosx ‎ C．asinx+bcosx D．acosx+bsinx ‎ ‎ ‎7． 如图，小山岗的斜坡AC的坡度是tanα=，在与山脚C距离200米的D处，测得山顶A的仰角为26.6°，则小山岗的高AB是（结果取整数，‎ 参考数据：sin26.6°=0.45，cos26.6°=0.89，tan26.6°=0.50）‎ A．300米 B．250米 ‎ C．400米 D．100米 ‎ ‎ ‎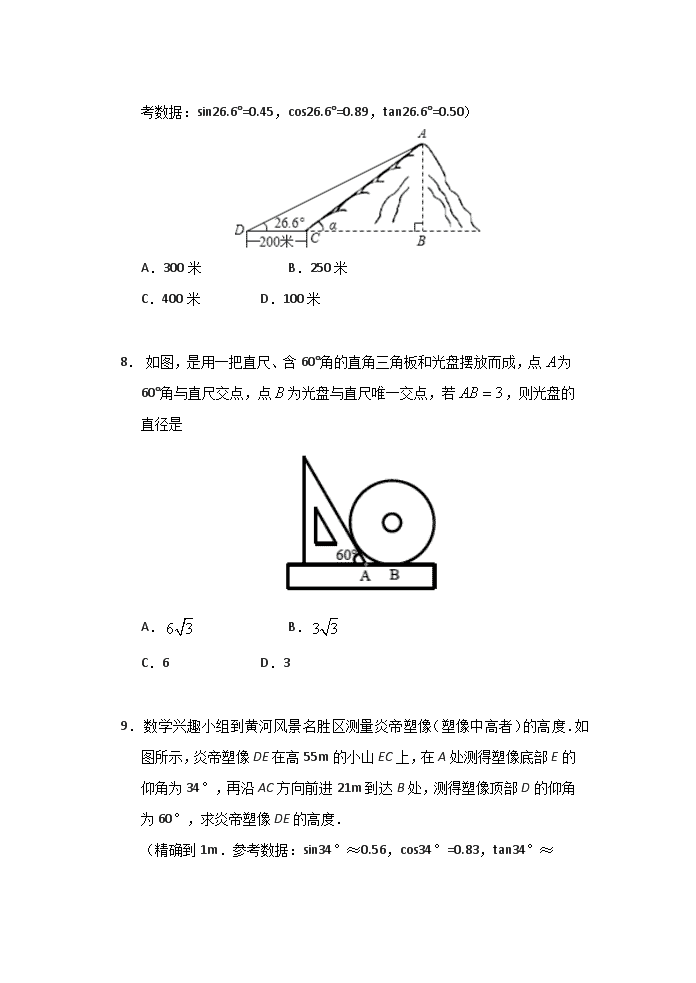8． 如图，是用一把直尺、含60°角的直角三角板和光盘摆放而成，点为60°角与直尺交点，点为光盘与直尺唯一交点，若，则光盘的直径是 A． B． ‎ C．6 D．3‎ ‎ ‎ ‎9． 数学兴趣小组到黄河风景名胜区测量炎帝塑像（塑像中高者）的高度．如图所示，炎帝塑像DE在高55m的小山EC上，在A处测得塑像底部E的仰角为34°，再沿AC方向前进21m到达B处，测得塑像顶部D的仰角为60°，求炎帝塑像DE的高度．‎ ‎（精确到1m．参考数据：sin34°≈0.56，cos34°=0.83，tan34°≈‎ ‎0.67，≈1.73）‎ ‎ ‎ ‎10． 筒车是我国古代发明的一种水利灌溉工具．如图1，明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理．如图2，筒车盛水桶的运行轨迹是以轴心O为圆心的圆．已知圆心在水面上方，且圆被水面截得的弦AB长为6米，∠OAB=41.3°，若点C为运行轨道的最高点（C，O的连线垂直于AB），求点C到弦AB所在直线的距离．‎ ‎（参考数据：sin41.3°≈0.66，cos41.3°≈0.75，tan41.3°≈0.88）‎ ‎ ‎ ‎11． 图2，图3是某公共汽车双开门的俯视示意图，ME、EF、FN是门轴的滑动轨道，∠E=∠F=90°，两门AB、CD的门轴A、B、C、D都在滑动轨 道上，两门关闭时（图2），A、D分别在E、F处，门缝忽略不计（即B、C重合）；两门同时开启，A、D分别沿E→M，F→N的方向匀速滑动，带动B、C滑动：B到达E时，C恰好到达F，此时两门完全开启，已知AB=50cm，CD=40cm．‎ ‎（1）如图3，当∠ABE=30°时，BC=__________cm．‎ ‎（2）在（1）的基础上，当A向M方向继续滑动15cm时，四边形ABCD的面积为__________cm2．‎ ‎ ‎ ‎12． 如图，九年级学生在一次社会实践活动中参观了具有深厚文化底蕴的观音山后感概万千，这座观音多高呢？为了测量这座观音像的高度AB，数学兴趣小组在C处用高为1.5米的测角仪CE，测得塔顶A角为42°，再向观音像方向前进12米，又测得观音像的顶端A的仰角为61°，求这座观音像的高度AB．‎ ‎（参考数据：sin42°≈0.67，tan42°≈0.90，sin61°≈0.87，tan61°≈1.80，结果保留整数）‎ ‎ ‎ ‎13． 如图，海面上一艘船由西向东航行，在A处测得正东方向上一座灯塔的最高点C的仰角为31°，再向东继续航行30m到达B处，测得该灯塔的最高点C的仰角为45°，根据测得的数据，计算这座灯塔的高度CD（结果取整数）．参考数据：sin31°≈0.52，cos31°≈0.86，tan31°≈0.60．‎ ‎ ‎ ‎14． 某挖掘机的底座高AB=0.8米，动臂BC=1.2米，CD=1.5米，BC与CD的固定夹角∠BCD=140°．初始位置如图1，斗杆顶点D与铲斗顶点E所在直线DE垂直地面AM于点E，测得∠CDE=70°（示意图2）．工作时如图3，动臂BC会绕点B转动，当点A，B，C在同一直线时，斗杆顶点D升至最高点（示意图4）．‎ ‎（1）求挖掘机在初始位置时动臂BC与AB的夹角∠ABC的度数．‎ ‎（2）问斗杆顶点D的最高点比初始位置高了多少米？（精确到0.1米）‎ ‎（参考数据：sin50°≈0.77，cos50°≈0.64，sin70°≈0.94，cos70°≈0.34，1.73）‎ ‎ ‎ ‎15． 如图，某货船以24海里/时的速度将一批货物从处运往正东方向的处，在点处测得某岛在北偏东60°的方向上．该货船航行30分钟后到达处，此时再测得该岛在北偏东30°的方向上，‎ ‎（1）求的度数；‎ ‎（2）已知在岛周围9海里的区域内有暗礁．若继续向正东方向航行，该货船有无触礁危险？试说明理由．（参考：，）‎ ‎ ‎ 答案 ‎1． 或 ‎2． 40°‎ ‎3． 1.5‎ ‎4． ‎ ‎5． A ‎6． D ‎7． A ‎8． A ‎9． ∵∠ACE=90°，∠CAE=34°，CE=55m，‎ ‎∴tan∠CAE=，∴AC==≈82.1（m），‎ ‎∵AB=21m，∴BC=AC–AB=61.1（m），‎ 在Rt△BCD中，tan60°==，‎ ‎∴CD=BC≈1.73×61.1≈105.7（m），‎ ‎∴DE=CD–EC=105.7–55≈51（m）.‎ 答：炎帝塑像DE的高度约为51m．‎ ‎10． 如图，连接CO并延长，与AB交于点D，‎ ‎∵CD⊥AB，∴AD=BD=AB=3（米），‎ 在Rt△AOD中，∠OAB=41.3°，‎ ‎∴cos41.3°=，即OA===4（米），‎ tan41.3°=，即OD=AD•tan41.3°=3×0.88=2.64（米），‎ 则CD=CO+OD=4+2.64=6.64（米）．‎ ‎11． （1）90﹣45；（2）2256．‎ ‎12． 如图，记EF的延长线交CD于H，‎ 根据题意得：BH=CE=DF=1.5 m，EF=CD=12 m，‎ 设AH=x，‎ 在Rt△AEH中，∠AEH=42°，AH=x，‎ ‎∴EH==，‎ 在Rt△AFH中，∠AFH=61°，AH=x，‎ ‎∴FH==，‎ ‎∵EF=EH-FH==12，‎ ‎∴x=21.6，‎ ‎∴AB=1.5+21.6≈23 m，‎ 答：这座观音像的高度AB是23 m．‎ ‎13． 在Rt△CAD中，tan∠CAD=，‎ 则AD=≈CD，‎ 在Rt△CBD中，∠CBD=45°，∴BD=CD，‎ ‎∵AD=AB+BD，∴CD=CD+30，解得CD=45，‎ 答：这座灯塔的高度CD约为45m．‎ ‎14． （1）过点C作CG⊥AM于点G，如图1，‎ ‎∵AB⊥AM，DE⊥AM，∴AB∥CG∥DE，‎ ‎∴∠DCG=180°–∠CDE=110°，‎ ‎∴BCG=∠BCD–∠GCD=30°，‎ ‎∴∠ABC=180°–∠BCG=150°；‎ ‎（2）过点C作CP⊥DE于点P，过点B作BQ⊥DE于点Q，交CG于点N，如图2，‎ 在Rt△CPD中，DP=CD×cos70°≈0.51（米），‎ 在Rt△BCN中，CN=BC×cos30°≈1.04（米），‎ 所以，DE=DP+PQ+QE=DP+CN+AB=2.35（米），‎ 如图3，过点D作DH⊥AM于点H，过点C作CK⊥DH于点K，‎ 在Rt△CKD中，DK=CD×sin50°≈1.16（米），‎ 所以，DH=DK+KH=3.16（米），‎ 所以，DH–DE≈0.8（米），‎ 所以，斗杆顶点D的最高点比初始位置约高了0.8米．‎ ‎15． （1）∵，，‎ ‎∴．‎ ‎（2）如图，过点作于，‎ 由题意，，，‎ ‎∴，‎ ‎∴，‎ ‎∴（海里），‎ 在中，，‎ ‎∴，‎ ‎∵．‎ 所以货船继续向正东方向行驶无触礁危险． ‎