2009年北京市西城区中考数学二模试卷 12页

‎5 2009年北京市西城区中考数学二模试卷 一、选择题(本题共32分，每小题4分)‎ ‎1．－5的绝对值等于( )‎ A．5 B．－‎5 ‎C． D．‎ ‎2．27的平方根等于( )‎ A．3 B． C．±3 D．‎ ‎3．若两圆的半径分别为‎1cm和‎5cm，圆心距为‎4cm，则这两圆的位置关系是( )‎ A．内切 B．相交 C．外切 D．外离 ‎4．用配方法将代数式a2＋‎4a－5变形，结果正确的是( )‎ A．(a＋2)2－1 B．(a＋2)2－‎5 ‎C．(a＋2)2＋4 D．(a＋2)2－9‎ ‎5．若圆锥的底面半径为‎3cm，母线为‎6cm，则圆锥的侧面积等于( )‎ A．36πcm2 B．27πcm‎2 ‎C．18πcm2 D．9πcm2‎ ‎6．如图，⊙O中，弦AB的长为2，OC⊥AB于C，OC＝1．若从⊙O外一点P作⊙O的两条切线，切点恰好分别为A、B，则∠APB的度数等于( )‎ A．120° B．90° C．60° D．45°‎ ‎ ‎ 第6题图 第7题图 ‎7．如图，菱形ABCD中，∠A＝30°，AD＝2，若菱形FBCE与菱形ABCD关于BC所在直线对称，则平行线AD与FE间的距离等于( )‎ A． B． C．2 D．4‎ ‎8．已知关于x的一次函数，其中实数k满足0＜k＜1．当自变量x在1≤x≤2的范围内变化时，此函数的最大值为( )‎ A．1 B．‎2 ‎C．k D．‎ 二、填空题(本题共16分，每小题4分)‎ ‎9．若分式的值为0，则x的值为________．‎ ‎10．如图，矩形ABCD中，两条对角线的交点为O，若OA＝5，AB＝6，则AD＝________．‎ 第10题图 ‎11．在函数中，自变量x的取值范围是________．‎ ‎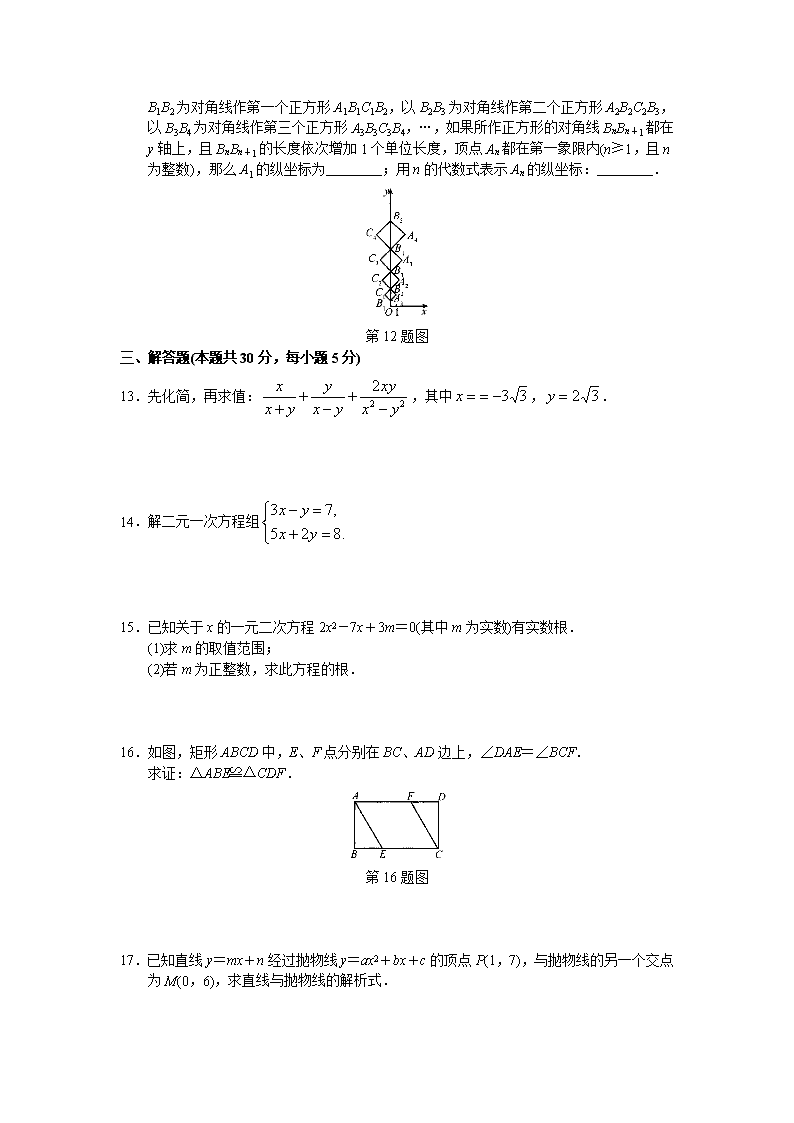12．如图，在平面直角坐标系：xOy中，B1(0，1)，B2(0，3)，B3(0，6)，B4(0，10)，…，以 B1B2为对角线作第一个正方形A1B‎1C1B2，以B2B3为对角线作第二个正方形A2B‎2C2B3，以B3B4为对角线作第三个正方形A3B‎3C3B4，…，如果所作正方形的对角线BnBn＋1都在y轴上，且BnBn＋1的长度依次增加1个单位长度，顶点An都在第一象限内(n≥1，且n为整数)，那么A1的纵坐标为________；用n的代数式表示An的纵坐标：________．‎ 第12题图 三、解答题(本题共30分，每小题5分)‎ ‎13．先化简，再求值：，其中，．‎ ‎14．解二元一次方程组 ‎15．已知关于x的一元二次方程2x2－7x＋‎3m＝0(其中m为实数)有实数根．‎ ‎(1)求m的取值范围；‎ ‎(2)若m为正整数，求此方程的根．‎ ‎16．如图，矩形ABCD中，E、F点分别在BC、AD边上，∠DAE＝∠BCF．‎ 求证：△ABE≌△CDF．‎ 第16题图 ‎17．已知直线y＝mx＋n经过抛物线y＝ax2＋bx＋c的顶点P(1，7)，与抛物线的另一个交点为M(0，6)，求直线与抛物线的解析式．‎ ‎18．如图，Rt△ABC中，∠ACB＝90°，AC＝‎2cm，∠A＝60°．将△ABC沿AB边所在直线向右平移，记平移后它的对应三角形为△DEF．‎ ‎(1)若将△ABC沿直线AB向右平移‎3cm，求此时梯形CAEF的面积；‎ ‎(2)若使平移后得到的△CDF是直角三角形，则△ABC平移的距离应为________cm．‎ 第18题图 四、解答题(本题共20分，第19题6分，第20题5分，第21题5分，第22题4分)‎ ‎19．某地一商场贴出五一期间的促销海报，内容如图所示．某校一个课外实践活动小组的同学在商场促销活动期间，在该商场门口随机调查了参与促销活动的部分顾客抽奖的情况，以下是根据其中200人次的抽奖情况画出的统计图的一部分：‎ 第19题图 ‎(1)补全获奖情况频数统计图；‎ ‎(2)求所调查的200人次抽奖的中奖率；‎ ‎(3)如果促销活动期间商场每天约有2000人次抽奖，请根据调查情况估计，该商场一天送出的购物券的总金额是多少元．‎ ‎20．列方程解应用题：‎ 某城市在道路改造过程中，需要铺设一条长为‎1500m的管道，为了尽量减少施工对交通造成的影响，实际施工时，工作效率比原计划提高了20％，结果提前2天完成了任务．求实际每天铺设了多少米管道．‎ ‎21．如图，等腰△ABC中，AC＝BC，⊙O为△ABC的外接圆，D为上一点，CE⊥AD于E．‎ 求证：AE＝BD＋DE．‎ 第21题图 ‎22．以下两图是一个等腰Rt△ABC和一个等边△DEF，要求把它们分别分割成三个三角形，使分得的三个三角形互相没有重叠部分，并且△ABC中分得的三个小三角形和△DEF中分得的三个小三角形分别相似．请画出两个三角形中的分割线，标出分割得到的小三角形中两个角的度数．‎ 第22题图 五、解答题(本题共22分，第23题7分，第24题8分，第25题7分)‎ ‎23．如图，正方形ABCD的边长为4，E为CD的中点，F为AD边上一点，且不与点D重合，AF＝a．‎ ‎(1)判断四边形BCEF的面积是否存在最大或最小值，若存在，求出最大或最小值；若不存在，请说明理由；‎ ‎(2)若∠BFE＝∠FBC，求tan∠AFB的值；‎ ‎(3)在(2)的条件下，若将“E为CD的中点”改为“CE＝k·DE”，其中k是为正整数，其他条件不变，请直接写出tan∠AFB的值．(用k的代数式表示)‎ 第23题图 ‎24．如图，抛物线y＝ax2＋bx＋c的顶点为A(0，1)，与x轴的一个交点B的坐标为(2，0)．点P在抛物线上，它的横坐标为2n(0＜n＜1)，作PC⊥x轴于C，PC交射线AB于点D．‎ ‎(1)求抛物线的解析式；‎ ‎(2)用n的代数式表示CD、PD的长，并通过计算说明与的大小关系；‎ ‎(3)若将原题中“0＜n＜‎1”‎的条件改为“n＞‎1”‎，其他条件不变，请通过计算说明(2)中的结论是否仍然成立．‎ 第24题图 ‎25．△ABC是等边三角形，P为平面内的一个动点，BP＝BA，若0°＜∠PBC＜180°，且∠PBC平分线上的一点D满足DB＝DA，‎ ‎(1)当BP与BA重合时(如图①)，∠BPD＝________°；‎ ‎(2)当BP在∠ABC的内部时(如图②)，求∠BPD的度数；‎ ‎(3)当BP在∠ABC的外部时，请你直接写出∠BPD的度数，并画出相应的图形．‎ 第25题图 答 案 ‎5．2009年北京市西城区中考数学二模试卷 一、选择题 ‎1．A 2．D 3．A 4．D 5．C 6．B 7．C 8．C 二、填空题 ‎9．－2 10．8 11.x≥2 12．2 ‎ 三、解答题 ‎13．解：‎ ‎．‎ 当x＝－3，y＝2时，x＋y＝－，x－y＝－5，．‎ ‎14．解：‎ 由①得y＝3x－7． ③‎ 把③代入②，得5x＋2(3x－7)＝8．‎ 解得x＝2．‎ 把x＝2代入③，得y＝－1．‎ ‎∴原方程组的解为 ‎15．解：(1)∵关于x的一元二次方程2x2－7x＋‎3m＝0(其中m为实数)有实数根，‎ Δ＝(－7)2－4×2×‎3m＝49－‎24m，‎ ‎∴49－‎24m≥0．‎ 解得．‎ ‎(2)当m为正整数时，m＝1或m＝2．‎ 当m＝1时，原方程化为2x2－7x＋3＝0，解得，x2＝3；‎ 当m＝2时，原方程化为2x2－7x＋6＝0，解得，x2＝2．‎ ‎16．证明：如图．‎ 第16题答图 ‎∵ABCD是矩形，∴AB＝CD，‎ ‎∠BAD＝∠B＝∠BCD＝∠D＝90°．‎ ‎∵∠DAE＝∠BCF，‎ ‎∴∠BAD－∠DAE＝∠BCD－∠BCF，‎ 即∠BAE＝∠DCF．‎ 在△ABE和△CDF中，‎ ‎∴△ABE≌△CDF．‎ ‎17．解：(1)∵直线y＝mx＋n经过点P(1，7)、M(0，6)，‎ 解得 ‎∴直线的解析式为y＝x＋6．‎ ‎∵抛物线y＝ax2＋bx＋c的顶点为P(1，7)，‎ ‎∴y＝a(x－1)2＋7．‎ ‎∵抛物线经过点M(0，6)，‎ ‎∴a(0－1)2＋7＝6，解得a＝－1．‎ ‎∴抛物线的解析式为y＝－x2＋2x＋6．‎ ‎18．解：(1)如图，作CG⊥AB于G．‎ 第18题答图 ‎∵Rt△ABC中，∠ACB＝90°，AC＝2，∠A＝60°，‎ ‎，CG＝AC·sin60°＝cm．‎ ‎∵△DEF是将△ABC沿AB边所在直线向右平移‎3cm得到，‎ ‎∴AD＝CF＝BE＝‎3cm，AE＝AB＋BE＝‎7cm．‎ ‎∴S梯形CAEF＝(CF＋AE)×CG＝(3＋7)×＝‎5cm2．‎ ‎(2)△ABC平移的距离应为1或‎4cm．‎ 四、解答题 ‎19．解：(1)答案见下图；‎ 第19题答图 ‎(2)所调查的200人次抽奖的中奖率为．‎ ‎(3)(元)．‎ 答：根据调查情况估计，该商场一天送出的购物券的总金额是13350元．‎ ‎20．解：设原计划每天铺设管道xm．‎ 则实际每天铺设管道(1＋20％)xm．‎ 由题意得．‎ 整理，得．解得x＝125．‎ 经检验，x＝125是原方程的解．‎ 所以．‎ 答：实际每天铺设了‎150m管道．‎ ‎21．证明：如图，在AE上截取AF＝BD，连结CF、CD．在△ACF和△BCD中，‎ 第21题答图 ‎∴△ACF≌△BCD．‎ ‎∴CF＝CD．‎ ‎∵CE⊥AD于E，∴EF＝DE．‎ ‎∴AE＝AF＋EF＝BD＋DE．‎ ‎22．答案不唯一，以下四个答案供参考：‎ 答案一： 答案二：‎ 答案三： 答案四：‎ 第22题答图 说明：各图中第一对相似三角形画正确得2分，三对相似三角形全部画正确得4分 五、解答题 ‎23．解：(1)如图①，S四边形BCEF＝S正方形ABCD－S△ABF－S△DEF .‎ ‎∵F为AD边上一点，且不与点D重合，‎ ‎∴ 0≤a＜4．‎ ‎∴当点F与点A重合时，a＝0，S四边形BCEF存在最大值12；‎ S四边形BCEF不存在最小值．‎ ‎①‎ ‎②‎ 第23题答图 ‎(2)如图②，延长BC、FE交于点P．‎ ‎∵正方形ABCD，‎ ‎∴AD∥BC．‎ ‎∴△DEF∽△CEP．‎ ‎∵E为CD的中点，‎ ‎，．‎ ‎∵∠BFE＝∠FBC，‎ ‎∴PB＝PF．‎ ‎∵AF＝a，‎ ‎∴PC＝DF＝4－a，PB＝PF＝8－a，．‎ ‎∵Rt△DEF中，EF2＝DE2＋DF2，．‎ 整理，得‎3a2－‎16a＋16＝0．‎ 解得，．‎ ‎∵F点不与D点重合，‎ ‎∴a＝4不成立，，．‎ ‎(3)tan∠AFB＝2k＋1．(k为正整数)‎ ‎24．解：(1)如图①．‎ 第24题答图 ‎∵抛物线y＝ax2＋bx＋c的顶点为A(0，1)，经过(2，0)点，‎ ‎∴y＝ax2＋1，‎ 又‎4a＋1＝0，解得．‎ ‎∴抛物线的解析式为．‎ ‎(2)设直线AB的解析式为y＝kx＋b．‎ ‎∵A(0，1)，B(2，0)．‎ 解得 ‎∴直线AB的解析式为．‎ ‎∵点P在抛物线上，它的横坐标为2n(0＜n＜1)，‎ ‎∴点P的坐标为(2n，1－n2)，且点P在第一象限．‎ 又∵PC⊥x轴于C，PC交射线AB于点D，‎ ‎∴xD＝OC＝2n，，且点D在第一象限．‎ ‎∴CD＝1－n．‎ PD＝yP－yD＝(1－n2)－(1－n)＝n－n2＝n(1－n)．‎ ‎∵0＜n＜1．‎ ‎．‎ ‎，‎ ‎．‎ ‎(3)当n＞1时，P、D两点在第四象限，且P点在D点下方(如图②)，yD＞yP．‎ 点P的坐标为(2n，1－n2)．‎ ‎∵xD＝OC＝2n，‎ ‎．‎ ‎∵D点在第四象限，‎ ‎∴CD＝－yD＝n－1，‎ PD＝yD－yP＝(1－n)－(1－n2)＝n(n－1)．‎ ‎∵n＞1，‎ ‎，‎ ‎，仍然成立．‎ ‎25．解：(1)∠BPD＝30°．‎ ‎(2)如图①，连结CD．‎ 方法一：∵点D在∠PBC的平分线上，‎ ‎∴∠1＝∠2．‎ ‎∵△ABC是等边三角形，‎ ‎∴BA＝BC＝AC，∠ACB＝60°．‎ ‎∵BP＝BA，∴BP＝BC．‎ ‎∵BD＝BD，∴△PBD≌△CBD．‎ ‎∴∠BPD＝∠3．‎ ‎∵DB＝DA，BC＝AC，CD＝CD，‎ ‎∴△BCD≌△ACD．‎ ‎∴∠3＝∠4＝∠ACB＝30°．‎ ‎∴∠BPD＝30°．‎ 方法二：∵△ABC是等边三角形，‎ ‎∴BA＝BC＝AC．‎ ‎∵DB＝DA，∴CD垂直平分AB．∴∠3＝∠4∠ACB＝30°．‎ ‎∵BP＝BA，∴BP＝BC．‎ ‎∵点D在∠PBC的平分线上，‎ ‎∴△PBD与△CBD关于BD所在直线对称．‎ ‎∴∠BPD＝∠3．∴∠BPD＝30°．‎ ‎(3)∠BPD＝30°或150°．‎ 图形见图②、图③．‎ 说明：(i)两种情况各得1分；‎ ‎(ii)图①中，BD在∠ABC内部或外部的情况只需画出一种即可．‎ 第25题答图