2020中考数学复习基础小卷速测七二次函数的实际应用 5页

基础小卷速测（七） 二次函数的实际应用 一、选择题 ‎1．一小球被抛出后，距离地面的高度h(m)和飞行时间t(s)满足下面的函数关系式：h＝－5(t－1)2＋6，则小球距离地面的最大高度是( )‎ A．1 m B．5 m C．6 m D．7 m ‎2．竖直向上发射的小球的高度h(m)关于运动时间t(s)的函数表达式为h＝at2＋bt，其图象如图50所示，若小球在发射后第2 s与第6 s时的高度相等，则下列时刻中小球的高度最高的是( )‎ A．第3 s B．第3.5 s C．第4.2 s D．第6.5 s h/m t/s O ‎2‎ ‎6‎ 图50‎ y x 图53‎ B A O 单位：m ‎2‎ ‎0.5‎ 图5‎ ‎0.4‎ ‎3．在羽毛球比赛中，某次羽毛球的运动路线可以看作是抛物线y＝－x2＋bx＋c的一部分，如图53，其中出球点B离地面O点的距离是1 m，球落地点A到O点的距离是4 m，那么这条抛物线的解析式是( )‎ A．y＝－x2＋x＋1 B．y＝－x2＋x－1 ‎ C．y＝－x2－x＋1 D．y＝－x2－x－1‎ ‎4．用总长为32 m的篱笆墙围成一个扇形的花园．若使扇形的面积y m2最大，则扇形的半径x m等于( )‎ A．8 m B． m C． m D．15 m ‎5．如图5，某公园草坪的防护栏是由100段形状相同的抛物线组成的，为了牢固起见，每段防护栏需要间距0.4 m加设一根不锈钢的支柱，防护栏的最高点距底部0.5 m，则这条防护栏需要不锈钢支柱的总长度为( )‎ A．50 m B．100 m C．160 m D．200 m 二、填空题 ‎6．如图69的一座拱桥，当水面宽AB为12 m时，桥洞顶部离水面4 m，已知桥洞的拱形是抛物线，以水平方向为x轴，建立平面直角坐标系，若选取点A为坐标原点时的抛物线解析式是y＝－(x－6)2＋4，则选取点B为坐标原点时的抛物线的解析式是______．‎ A B ‎12 m ‎4 m 图69‎ ‎ ‎图30‎ ‎3m ‎6 m ‎8 m 5‎ ‎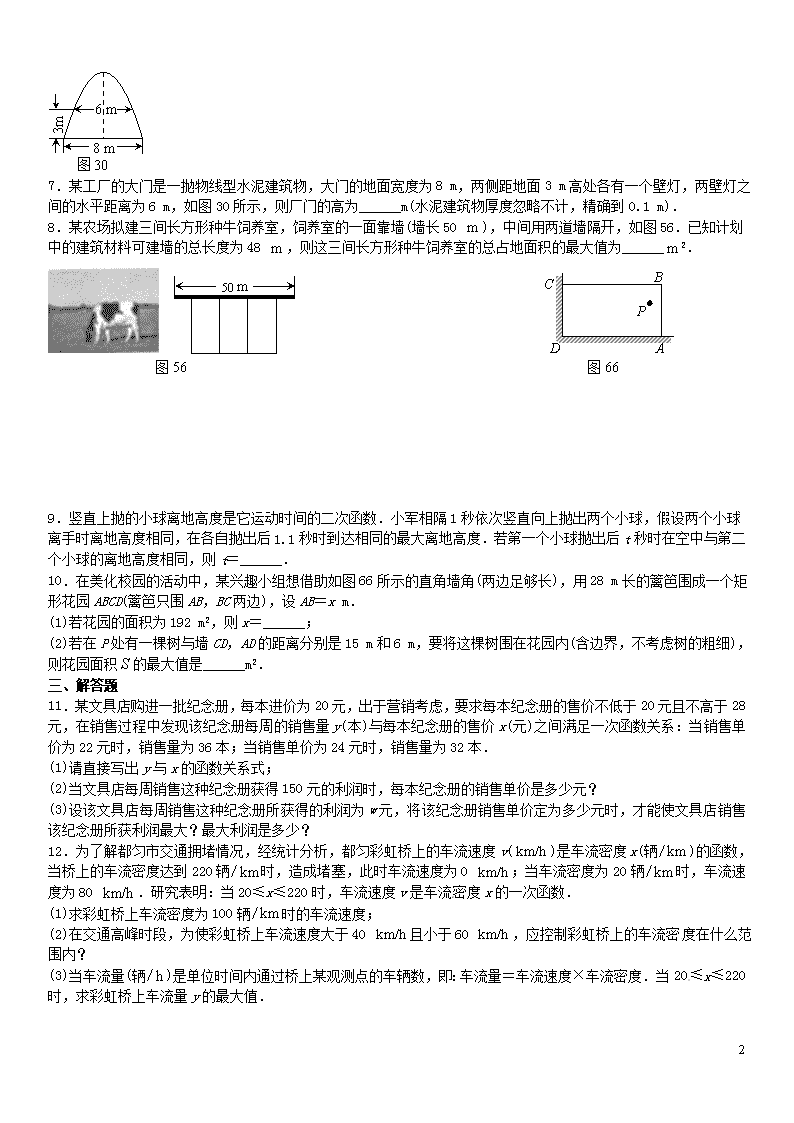7．某工厂的大门是一抛物线型水泥建筑物，大门的地面宽度为8 m，两侧距地面3 m高处各有一个壁灯，两壁灯之间的水平距离为6 m，如图30所示，则厂门的高为______m(水泥建筑物厚度忽略不计，精确到0.1 m)．‎ ‎8．某农场拟建三间长方形种牛饲养室，饲养室的一面靠墙(墙长50 )，中间用两道墙隔开，如图56．已知计划中的建筑材料可建墙的总长度为48 ，则这三间长方形种牛饲养室的总占地面积的最大值为______2．‎ 图56‎ ‎50 m P D C B A 图66‎ ‎ ‎ ‎9．竖直上抛的小球离地高度是它运动时间的二次函数．小军相隔1秒依次竖直向上抛出两个小球，假设两个小球离手时离地高度相同，在各自抛出后1.1秒时到达相同的最大离地高度．若第一个小球抛出后t秒时在空中与第二个小球的离地高度相同，则t＝______．‎ ‎10．在美化校园的活动中，某兴趣小组想借助如图66所示的直角墙角(两边足够长)，用28 m长的篱笆围成一个矩形花园ABCD(篱笆只围AB，BC两边)，设AB＝x m．‎ ‎(1)若花园的面积为192 m2，则x＝______；‎ ‎(2)若在P处有一棵树与墙CD，AD的距离分别是15 m和6 m，要将这棵树围在花园内(含边界，不考虑树的粗细)，则花园面积的最大值是______m2．‎ 三、解答题 ‎11．某文具店购进一批纪念册，每本进价为20元，出于营销考虑，要求每本纪念册的售价不低于20元且不高于28元，在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系：当销售单价为22元时，销售量为36本；当销售单价为24元时，销售量为32本．‎ ‎(1)请直接写出y与x的函数关系式；‎ ‎(2)当文具店每周销售这种纪念册获得150元的利润时，每本纪念册的销售单价是多少元？‎ ‎(3)设该文具店每周销售这种纪念册所获得的利润为w元，将该纪念册销售单价定为多少元时，才能使文具店销售该纪念册所获利润最大？最大利润是多少？‎ ‎12．为了解都匀市交通拥堵情况，经统计分析，都匀彩虹桥上的车流速度v()是车流密度x(辆/)的函数，当桥上的车流密度达到220辆/时，造成堵塞，此时车流速度为0 ；当车流密度为20辆/时，车流速度为80 ．研究表明：当20≤x≤220时，车流速度v是车流密度x的一次函数．‎ ‎(1)求彩虹桥上车流密度为100辆/时的车流速度；‎ ‎(2)在交通高峰时段，为使彩虹桥上车流速度大于40 且小于60 ，应控制彩虹桥上的车流密度在什么范围内？‎ ‎(3)当车流量(辆/)是单位时间内通过桥上某观测点的车辆数，即：车流量＝车流速度×车流密度．当20≤x≤220时，求彩虹桥上车流量y的最大值．‎ 5‎ ‎13．某店因为经营不善欠下38400元的无息贷款的债务，想转行经营服装专卖店又缺少资金．“梦想中国秀”栏目组决定借给该店30000元资金，并约定利用经营的利润偿还债务(所有债务均不计利息)．已知该店代理的品牌服装进价为每件40元，该品牌服装日销售量y(件)与销售价x(元/件)之间的关系可用图71中的一条折线(实线)来表示．该店应支付员工的工资为每人每天82元，每天还应支付其它费用为106元(不包含债务)．‎ y/件 x/元/件 O ‎40‎ ‎58‎ ‎71‎ ‎11‎ ‎24‎ ‎60‎ 图71‎ ‎(1)求日销售量(件)和销售价(元/件)之间的函数关系式；‎ ‎(2若该店暂不考虑偿还债务，当天的销售价为48元/件时，当天正好收支平衡(收入＝支出)，求该店员工的人数；‎ ‎(3)若该店只有2名员工，则该店最早需要多少天能还清所有债务，此时每件服装的价格应定为多少元？‎ 参考答案 1． C [解析]抛物线的顶点坐标是(1，6)． ‎ 2． C　[解析]抛物线的对称轴是t＝4．｜t－4｜越小，t所对应的高度h越大．故选C． ‎ ‎3．A [解析]将B(0，1)，A(4，0)代入y＝－x2＋bx＋c，得解得 ‎∴这条抛物线的解析式是y＝－x2＋x＋1，故选A． ‎ ‎4．A [解析]弧长为32－2x．y＝－x2＋16x＝－(x－8)2＋64，∴当x＝8时，扇形的面积最大．‎ ‎5．C　[解析]建立如图1所示的直角坐标系，设抛物线的解析式为y＝ax2＋b．将点(0，)和点(1，0)的坐标代入求得a＝－，b＝0.5，∴抛物线的解析式为y＝－x2＋．‎ 显然A点的坐标为(，0)，C点坐标为(，0)．把x＝代入抛物线解析式得y＝，即AB＝；把x＝代入抛物线解析式得y＝，即CD＝．‎ ‎∴这条防护栏需要不锈钢支柱的总长度为(＋)×2×100＝160(m)．‎ O 图1‎ A B C D x y 6． y＝－(x＋6)2＋4 ‎ 5‎ ‎7．6.9 [解析]以抛物线的对称轴为y轴，对称轴与地面的交点为坐标原点建立直角坐标系，则可设抛物线的解析式为y＝ax2＋h．∵抛物线经过点(－4，0)和(－3，3)．∴解得a＝，h＝≈6.9，∴厂门高约为6.9 m．‎ ‎8．432 [解析]设总占地面积为S 2，与墙垂直的边的长度为x ，‎ 则与墙平行的边的长度为(48－4x)，其中0＜x＜12．‎ ‎∴S＝x(48－x)＝－(x－24)2＋576．‎ ‎∵抛物线的开口向下，∴x＜24时，S随x的增大而增大．‎ ‎∴x＝12时，S可取得最大值，最大值为＝12×(48－12)＝432．‎ ‎9．1.6秒　[解析]设小球离地的高度为y米，则第一个小球y与t之间的关系式为 y1＝a(t－1.1)2＋h．‎ 第二个小球y与t之间的关系式为 y2＝a(t－1－1.1)2＋h，即y2＝a(t－2.1)2＋h．‎ 令y1＝y2，得a(t－1.1)2＋h＝a(t－2.1)2＋h，‎ 解得t＝1.6．‎ ‎10．(1)12或16；(2)195‎ ‎[解析](1)由题意，得x(28－x)＝192．‎ 解这个方程，得x1＝12，x2＝16．‎ ‎(2)花园面积S＝x(28－x)＝－(x－14)2＋196．‎ 由题意，知解得6≤x≤13．‎ 在6≤x≤13范围内，S随x的增大而增大．‎ ‎∴当x＝13时，S最大＝－(13－14) 2＋196＝195(m2)．‎ ‎11．解：(1)y＝－2x＋80。‎ ‎(2)设当文具店每周销售这种纪念册获得150元的利润时，每本纪念册的销售单价是x元，‎ 根据题意得：(x－20)y＝150，‎ 则(x－20)(－2x＋80)＝150，‎ 整理得：x2－60x＋875＝0，‎ ‎(x－25)(x－35)＝0，‎ 解得：x1＝25，x2＝35(不合题意，舍去)，‎ 答：每本纪念册的销售单价是25元.‎ ‎(3)由题意可得：‎ w＝(x－20)(－2x＋80)‎ ‎＝－2x2＋120x－1600‎ ‎＝－2(x－30)2＋200，‎ 此时当x＝30时，w最大，‎ 又∵售价不低于20元且不高于28元，‎ ‎∴x＜30时，y随x的增大而增大，即当x＝28时，w最大＝－2(28－30)2＋200＝192(元)，‎ 答：该纪念册销售单价定为28元时，才能使文具店销售该纪念册所获利润最大，最大利润是192元．‎ ‎12．解：(1)设车流速度v与车流密度x的函数关系为v＝kx＋b．由题意，得 解得 5‎ ‎∴当20≤x≤220时，v＝－x＋88．‎ 当x＝100时，v＝48()．‎ ‎(2)由题意，得 解得70＜x＜120．‎ ‎∴应控制大桥上的车流密度在70＜x＜120范围内．‎ ‎(3)当20≤x≤220时，‎ y＝vx＝(－x＋88)x＝－(x－110)2＋4840．‎ ‎∴当x＝110时，y最大＝4840．‎ ‎∴当车流密度是110辆/，车流量y取得最大值4840辆/．‎ ‎13．解：(1)当40≤x＜58时，设函数关系式为y＝kx＋b．‎ 把x＝40，y＝60和x＝58，y＝24分别代入y＝kx＋b，得 解得 所以y＝－2x＋140．‎ 当58x≤x≤71时，设函数关系式为y＝mx＋n．‎ 把x＝58，y＝24和x＝71，y＝11分别代入y＝mx＋n，得 解得 所以y＝－x＋82．‎ ‎(2)设该店员工为a人．‎ 把x＝48代入y＝－2x＋140，得y＝－2×48＋140＝44．‎ 由题意(48－40)×44＝82a＋106，解得a＝3．‎ 即该店员工为3人．‎ ‎(3)设该店每天的销售利润为W元，则W＝(x－40)y．‎ ‎①当40≤x＜58时，W＝(x－40)(－2x＋140)＝－2x2＋220x－5600．‎ 即W＝－2(x－55)2＋450．‎ 当x＝55时，W有最大值为450.‎ ‎②当58≤x≤71时，W＝(x－40)(－x＋82)＝－x2＋122x－3280．‎ 即W＝－(x－61)2＋441．‎ 当x＝61时，W有最大值为441．‎ 综上可知，当x＝55时，每天可获得最大利润450元．‎ ‎(38400＋30000)÷(450－82×2－106)＝380(天)．‎ 即该店最早需要380天能还清所有债务，此时每件服装的价格应定为55元．‎ 5‎