中考数学省卷压轴题汇总大全+中考数学专题训练精品等大全集 116页

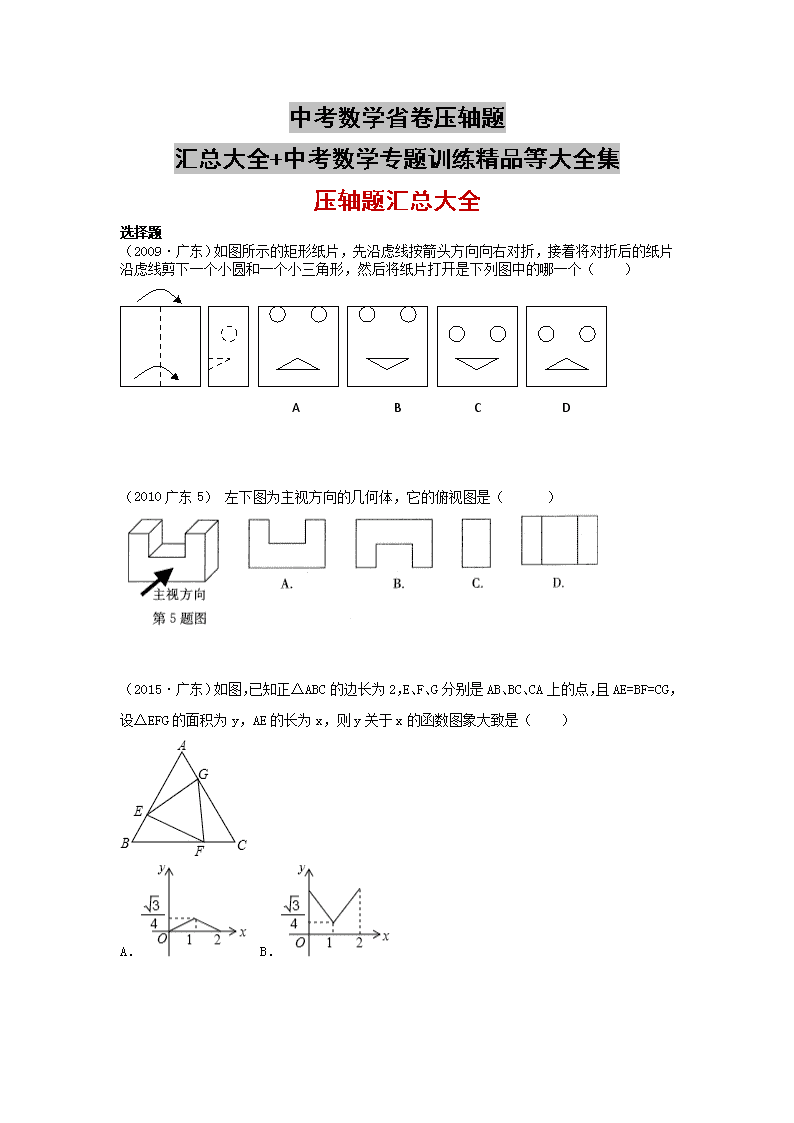
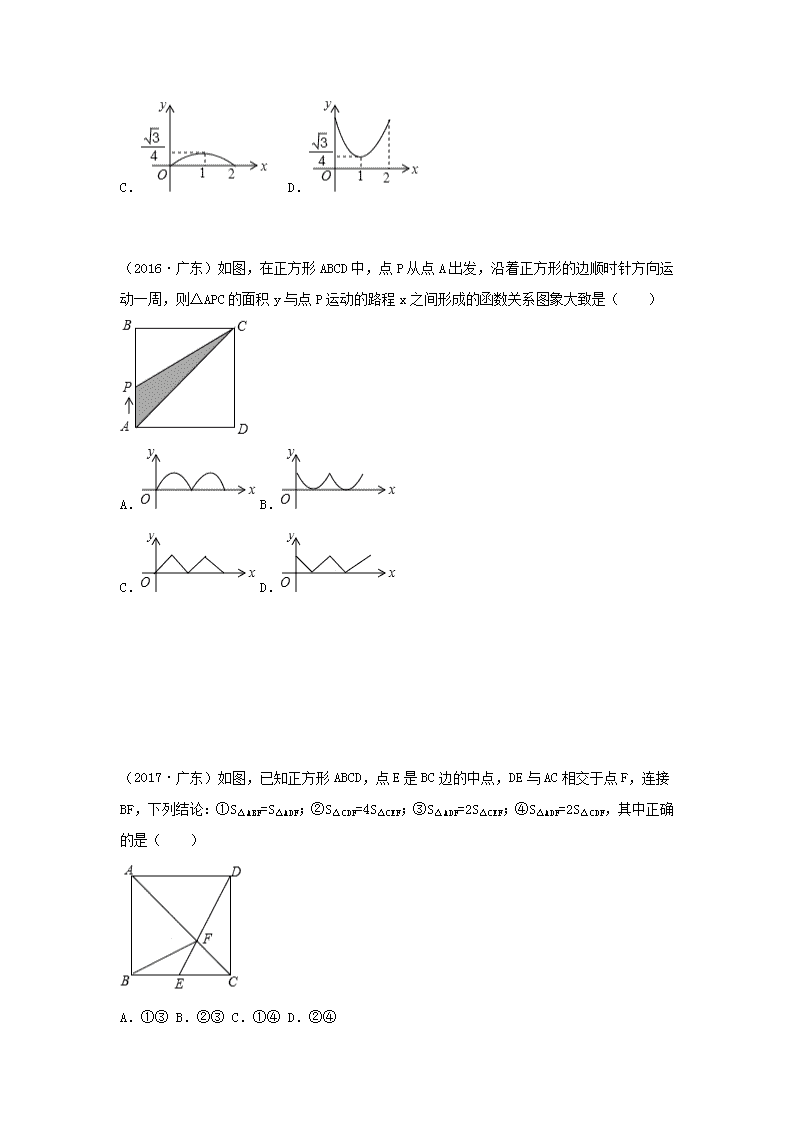
中考数学省卷压轴题 汇总大全+中考数学专题训练精品等大全集 压轴题汇总大全 选择题 （2009·广东）如图所示的矩形纸片，先沿虑线按箭头方向向右对折，接着将对折后的纸片 沿虑线剪下一个小圆和一个小三角形，然后将纸片打开是下列图中的哪一个（ ） C． D．A． B． （2010 广东 5） 左下图为主视方向的几何体，它的俯视图是（ ） （2015·广东）如图，已知正△ABC 的边长为 2，E、F、G 分别是 AB、BC、CA 上的点，且 AE=BF=CG， 设△EFG 的面积为 y，AE 的长为 x，则 y 关于 x 的函数图象大致是（ ） A． B． C． D． （2016·广东）如图，在正方形 ABCD 中，点 P 从点 A 出发，沿着正方形的边顺时针方向运 动一周，则△APC 的面积 y 与点 P 运动的路程 x 之间形成的函数关系图象大致是（ ） A． B． C． D． （2017·广东）如图，已知正方形 ABCD，点 E 是 BC 边的中点，DE 与 AC 相交于点 F，连接 BF，下列结论：①S△ABF=S△ADF；②S△CDF=4S△CEF；③S△ADF=2S△CEF；④S△ADF=2S△CDF，其中正确的是 （ ） A．①③ B．②③ C．①④ D．②④ （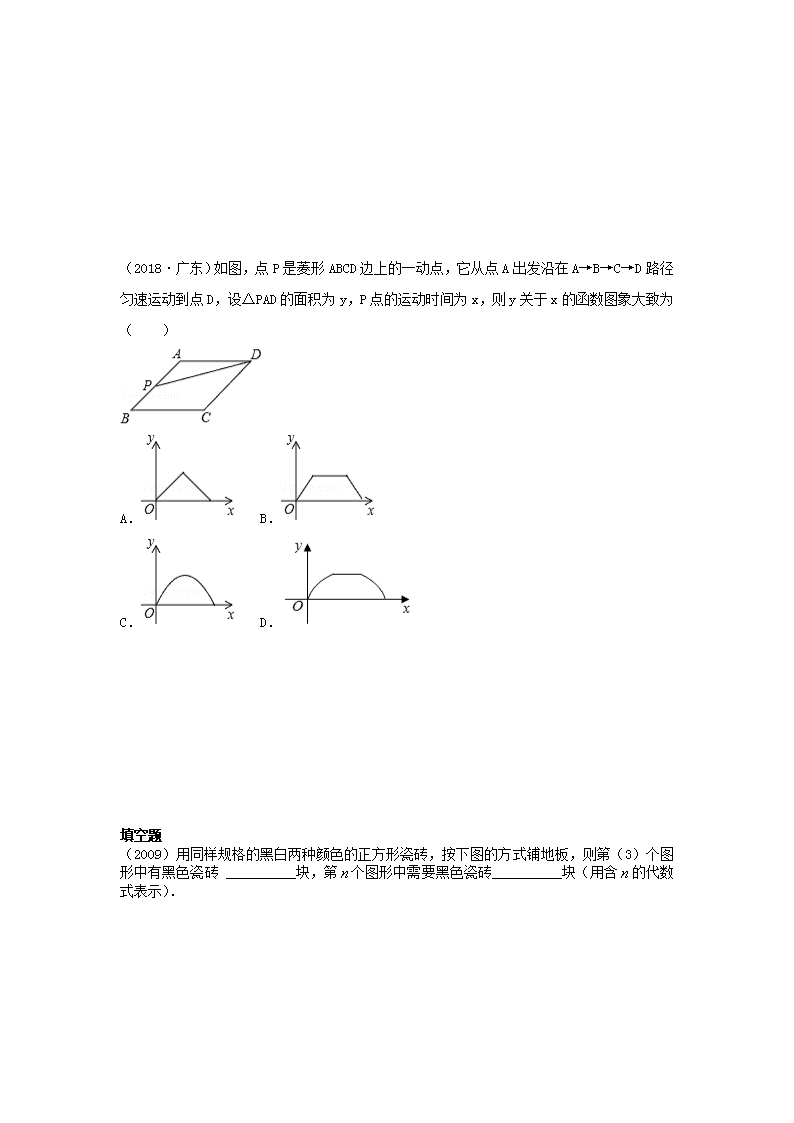2018·广东）如图，点 P 是菱形 ABCD 边上的一动点，它从点 A 出发沿在 A→B→C→D 路径 匀速运动到点 D，设△PAD 的面积为 y，P 点的运动时间为 x，则 y 关于 x 的函数图象大致为 （ ） A． B． C． D． 填空题 （2009）用同样规格的黑白两种颜色的正方形瓷砖，按下图的方式铺地板，则第（3）个图 形中有黑色瓷砖 __________块，第 n 个图形中需要黑色瓷砖__________块（用含 n 的代数 式表示）． （1） （2） （3） 第10题图 …… （2010 广东 10）如图（1），已知小正方形 ABCD 的面积为 1，把它的各边延长一倍得到新正 方形 A1B1C1D1； 把正方形 A1B1C1D1 边长按原法延长一倍得到新正方形 A2B2C2D2（如图（2））；以此下去…， 则正方形 A4B4C4D4 的面积为 ． （2011 广东 10）如图(1)，将一个正六边形各边延长，构成一个正六角星形 AFBDCE，它的 面积为 1；取△ABC 和△DEF 各边中点，连接成正六角星形 A1F1B1D1C1E1，如图(2)中阴影部 分；取△A1B1C1 和△D1E1F1 各边中点，连接成正六角星形 A2F2B2D2C2E2，如图(3)中阴影部分； 如此下去…，则正六角星形 A4F4B4D4C4E4 的面积为_________________． 题 10 图（1） A1 B C D A F E B C D A F E B C D A F E B1 C1 F1 D1 E1 A1 B1 C1 F1 D1 E1A2 B2 C2 F2 D2 E2 题 10 图（2） 题 10 图（3） （2012•广东）如图，在▱ ABCD 中，AD=2，AB=4，∠A=30°，以点 A 为圆心，AD 的长为半径 画弧交 AB 于点 E，连接 CE，则阴影部分的面积是 _________ （结果保留π）． （2013•广东）如图，三个小正方形的边长都为 1，则图中阴影部分面积的和是 _________ （结果保留π）． （2014•广东）如图， ABC 绕点 A 顺时针旋转 45 得到△ AB C  ，若 90BAC   ， 2AB AC  ，则图中阴影部分的面积等于 ． （2015.广东）如图，△ABC 三边的中线 AD、BE、CF 的公共点为 G，若 S△ABC=12，则图中阴影 部分的面积是 ． （2016·广东）如图，点 P 是四边形 ABCD 外接圆上任意一点，且不与四边形顶点重合，若 AD 是⊙O 的直径，AB=BC=CD．连接 PA、PB、PC，若 PA=a，则点 A 到 PB 和 PC 的距离之和 AE+AF= ． （2017·广东）如图，矩形纸片 ABCD 中，AB=5，BC=3，先按图（2）操作：将矩形纸片 ABCD 沿过点 A 的直线折叠，使点 D 落在边 AB 上的点 E 处，折痕为 AF；再按图（3）操作，沿过 点 F 的直线折叠，使点 C 落在 EF 上的点 H 处，折痕为 FG，则 A、H 两点间的距离为 ． （2018·广东）如图，已知等边△OA1B1，顶点 A1 在双曲线 y= （x＞0）上，点 B1 的坐标 为（2，0）．过 B1 作 B1A2∥OA1 交双曲线于点 A2，过 A2 作 A2B2∥A1B1 交 x 轴于点 B2，得到第二 个等边△B1A2B2；过 B2 作 B2A3∥B1A2 交双曲线于点 A3，过 A3 作 A3B3∥A2B2 交 x 轴于点 B3，得到 第三个等边△B2A3B3；以此类推，…，则点 B6 的坐标为 ． 解答题 （2009.广东）正方形 ABCD 边长为 4， M 、 N 分别是 BC 、CD 上的两个动点， 当 M 点在 BC 上运动时，保持 AM 和 MN 垂直， （1）证明： Rt RtABM MCN△ ∽ △ ； （2）设 BM x ，梯形 ABCN 的面积为 y ，求 y 与 x 之间的函数关系式；当 M 点运 动到什么位置时，四边形 ABCN 面积最大，并求出最大面积； （3）当 M 点运动到什么位置时 Rt RtABM AMN△ ∽ △ ，求此时 x 的值． D M A B C 第 22 题图 N （2010 广东 20）已知两个全等的直角三角形纸片 ABC、DEF，如图（1）放置，点 B、D 重合， 点 F 在 BC 上， AB 与 EF 交于点 G.∠C＝∠EFB＝90°，∠E＝∠ABC＝30°，AB＝DE＝4． （1）求证： EGB 是等腰三角形； （2）若纸片 DEF 不动，问 ABC 绕点 F 逆时针旋转最小____度时，四边形 ACDE 成为以 ED 为底的梯形（如图（2））．求此梯形的高． （2011 广东 22）如图，抛物线 14 17 4 5 2  xxy 与 y 轴交于 A 点，过点 A 的直线与抛 物 线交于另一点 B，过点 B 作 BC⊥x 轴，垂足为点 C(3，0). （1）求直线 AB 的函数关系式； （2）动点 P 在线段 OC 上从原点出发以每秒一个单位的速度向 C 移动，过点 P 作 PN⊥x 轴， 交直线 AB 于点 M，交抛物线于点 N. 设点 P 移动的时间为 t 秒，MN 的长度为 s 个单位，求 s 与 t 的函数关系式，并写出 t 的取值范围； （3）设在（2）的条件下（不考虑点 P 与点 O，点 C 重合的情况），连接 C M，BN，当 t 为何 值时，四边形 BCMN 为平行 四边形？问对于所求的 t 值，平行四边形 BCMN 是否菱形？ 请说 明理由. （2012•广东 21）如图，在矩形纸片 ABCD 中，AB=6，BC=8．把△BCD 沿对角线 BD 折叠，使 点 C 落在 C′处，BC′交 AD 于点 G；E、F 分别是 C′D 和 BD 上的点，线段 EF 交 AD 于点 H， 把△FDE 沿 EF 折叠，使点 D 落在 D′处，点 D′恰好与点 A 重合． （1）求证：△ABG≌△C′DG； （2）求 tan∠ABG 的值； （3）求 EF 的长． （2012•广东 22）如图，抛物线 y= x2﹣ x﹣9 与 x 轴交于 A、B 两点，与 y 轴交于点 C，连 接 BC、AC． （1）求 AB 和 OC 的长； （2）点 E 从点 A 出发，沿 x 轴向点 B 运动（点 E 与点 A、B 不重合），过点 E 作直线 l 平行 BC，交 AC 于点 D．设 AE 的长为 m，△ADE 的面积为 s，求 s 关于 m 的函数关系式，并写出自 变量 m 的取值范围； （3）在（2）的条件下，连接 CE，求△CDE 面积的最大值；此时，求出以点 E 为圆心，与 BC 相切的圆的面积（结果保留π）． （2013•广东 24）如图，⊙O 是 Rt△ABC 的外接圆，∠ABC=90°，弦 BD=BA，AB=12，BC=5， BE⊥DC 交 DC 的延长线于点 E． （1）求证：∠BCA=∠BAD； （2）求 DE 的长； （3）求证：BE 是⊙O 的切线． （2013•广东 25）有一副直角三角板，在三角板 ABC 中，∠BAC=90°，AB=AC=6，在三角板 DEF 中，∠FDE=90°，DF=4，DE= ．将这副直角三角板按如图 1 所示位置摆放，点 B 与 点 F 重合，直角边 BA 与 FD 在同一条直线上．现固定三角板 ABC，将三角板 DEF 沿射线 BA 方向平行移动，当点 F 运动到点 A 时停止运动． （1）如图 2，当三角板 DEF 运动到点 D 到点 A 重合时，设 EF 与 BC 交于点 M，则∠EMC= _________ 度； （2）如图 3，当三角板 DEF 运动过程中，当 EF 经过点 C 时，求 FC 的长； （3）在三角板 DEF 运动过程中，设 BF=x，两块三角板重叠部分的面积为 y，求 y 与 x 的函 数解析式，并求出对应的 x 取值范围． （2014•广东 24）如图， O 是 ABC 的外接圆， AC 是直径，过点 O 作OD AB 于点 D ， 延长 DO 交 O 于点 P ，过点 P 作 PE AC 于点 E ，作射线 DE 交 BC 的延长线于 F 点，连 接 PF ． （1）若 60POC   ， 12AC  ，求劣弧 PC 的长；（结果保留 ) （2）求证： OD OE ； （3）求证： PF 是 O 的切线． （2014•广东 25）如图，在 ABC 中，AB AC ，AD BC 于点 D ， 10BC cm ， 8AD cm ．点 P 从点 B 出发，在线段 BC 上以每秒3cm 的速度向点 C 匀速运动，与此同时，垂直于 AD 的 直线 m 从底边 BC 出发，以每秒 2cm 的速度沿 DA 方向匀速平移，分别交 AB 、 AC 、 AD 于 E 、 F 、 H ，当点 P 到达点 C 时，点 P 与直线 m 同时停止运动，设运动时间为 t 秒 ( 0)t  ． （1）当 2t  时，连接 DE 、 DF ，求证：四边形 AEDF 为菱形； （2）在整个运动过程中，所形成的 PEF 的面积存在最大值，当 PEF 的面积最大时，求 线段 BP 的长； （3）是否存在某一时刻t ，使 PEF 为直角三角形？若存在，请求出此时刻t 的值；若不存 在，请说明理由． （2015•广东 24）⊙O 是△ABC 的外接圆，AB 是直径，过 的中点 P 作⊙O 的直径 PG 交弦 BC 于点 D，连接 AG、CP、PB． （1）如图 1，若 D 是线段 OP 的中点，求∠BAC 的度数； （2）如图 2，在 DG 上取一点 K，使 DK=DP，连接 CK，求证：四边形 AGKC 是平行四边形； （3）如图 3，取 CP 的中点 E，连接 ED 并延长 ED 交 AB 于点 H，连接 PH，求证：PH⊥AB． （2015•广东 25）如图，在同一平面上，两块斜边相等的直角三角板 Rt△ABC 和 Rt△ADC 拼 在一起，使斜边 AC 完全重合，且顶点 B，D 分别在 AC 的两旁，∠ABC=∠ADC=90°，∠CAD=30°， AB=BC=4cm （1）填空：AD= （cm），DC= （cm） （2）点 M，N 分别从 A 点，C 点同时以每秒 1cm 的速度等速出发，且分别在 AD，CB 上沿 A →D，C→B 方向运动，当 N 点运动到 B 点时，M、N 两点同时停止运动，连接 MN，求当 M、N 点运动了 x 秒时，点 N 到 AD 的距离（用含 x 的式子表示） （3）在（2）的条件下，取 DC 中点 P，连接 MP，NP，设△PMN 的面积为 y（cm2），在整个运 动过程中，△PMN 的面积 y 存在最大值，请求出 y 的最大值． （参考数据 sin75°= ，sin15°= ） （2016·广东 24）如图，⊙O 是△ABC 的外接圆，BC 是⊙O 的直径，∠ABC=30°，过点 B 作 ⊙O 的切线 BD，与 CA 的延长线交于点 D，与半径 AO 的延长线交于点 E，过点 A 作⊙O 的切 线 AF，与直径 BC 的延长线交于点 F． （1）求证：△ACF∽△DAE； （2）若 S△AOC= ，求 DE 的长； （3）连接 EF，求证：EF 是⊙O 的切线． （2016·广东 25）如图，BD 是正方形 ABCD 的对角线，BC=2，边 BC 在其所在的直线上平移， 将通过平移得到的线段记为 PQ，连接 PA、QD，并过点 Q 作 QO⊥BD，垂足为 O，连接 OA、OP． （1）请直接写出线段 BC 在平移过程中，四边形 APQD 是什么四边形？ （2）请判断 OA、OP 之间的数量关系和位置关系，并加以证明； （3）在平移变换过程中，设 y=S△OPB，BP=x（0≤x≤2），求 y 与 x 之间的函数关系式，并求 出 y 的最大值． （2017·广东 24）如图，AB 是⊙O 的直径，AB=4 ，点 E 为线段 OB 上一点（不与 O，B 重 合），作 CE⊥OB，交⊙O 于点 C，垂足为点 E，作直径 CD，过点 C 的切线交 DB 的延长线于点 P，AF⊥PC 于点 F，连接 CB． （1）求证：CB 是∠ECP 的平分线； （2）求证：CF=CE； （3）当 = 时，求劣弧 的长度（结果保留π） （2017·广东 25）如图，在平面直角坐标系中，O 为原点，四边形 ABCO 是矩形，点 A，C 的坐标分别是 A（0，2）和 C（2 ，0），点 D 是对角线 AC 上一动点（不与 A，C 重合），连 结 BD，作 DE⊥DB，交 x 轴于点 E，以线段 DE，DB 为邻边作矩形 BDEF． （1）填空：点 B 的坐标为 ； （2）是否存在这样的点 D，使得△DEC 是等腰三角形？若存在，请求出 AD 的长度；若不存 在，请说明理由； （3）①求证： = ； ②设 AD=x，矩形 BDEF 的面积为 y，求 y 关于 x 的函数关系式（可利用①的结论），并求出 y 的最小值． （2018·广东 24）如图，四边形 ABCD 中，AB=AD=CD，以 AB 为直径的⊙O 经过点 C，连接 AC、 OD 交于点 E． （1）证明：OD∥BC； （2）若 tan∠ABC=2，证明：DA 与⊙O 相切； （3）在（2）条件下，连接 BD 交⊙O 于点 F，连接 EF，若 BC=1，求 EF 的长． （2018·广东 24）已知 Rt△OAB，∠OAB=90°，∠ABO=30°，斜边 OB=4，将 Rt△OAB 绕点 O 顺时针旋转 60°，如图 1，连接 BC． （1）填空：∠OBC= °； （2）如图 1，连接 AC，作 OP⊥AC，垂足为 P，求 OP 的长度； （3）如图 2，点 M，N 同时从点 O 出发，在△OCB 边上运动，M 沿 O→C→B 路径匀速运动，N 沿 O→B→C 路径匀速运动，当两点相遇时运动停止，已知点 M 的运动速度为 1.5 单位/秒， 点 N 的运动速度为 1 单位/秒，设运动时间为 x 秒，△OMN 的面积为 y，求当 x 为何值时 y 取得最大值？最大值为多少？ 专题训练(二) [多结论题] 1.[2017·遵义] 如图 ZT2-1,抛物线 y=ax2+bx+c 经过点(-1,0),对称轴 l 如图所示.则下列结 论:①abc>0;②a-b+c=0;③2a+c<0;④a+b<0,其中所有正确的结论是( ) 图 ZT2-1 A.①③ B.②③ C.②④ D.②③④ 2.如图 ZT2-2,抛物线 y=ax2+bx+c(a≠0)的对称轴为直线 x=-2,与 x 轴的一个交点在(-3,0)和(-4,0) 之间,其部分图象如图所示,则下列结论:①4a-b=0;②c<0;③-3a+c>0;④4a-2b>at2+bt(t 为实 数);⑤点 - ,y1 , - ,y2 , - ,y3 是该抛物线上的点,则 y10.∵抛物线与 y 轴正半轴相交,∴c>0,即 abc<0,结论①错误.∵抛物线 y=ax2+bx+c 经过点(-1,0),∴a-b+c=0, 结论②正确.∵当 x=2 时,y<0,即 4a+2b+c<0,又 b=a+c,∴4a+2(a+c)+c<0,即 2a+c<0,结论③正 确.∵c=b-a,∴a+b<0,结论④正确. 2.C [解析] ∵抛物线 y=ax2+bx+c(a≠0)的对称轴为直线 x=-2,∴- =-2,∴4a-b=0,故①正确; ∵抛物线 y=ax2+bx+c(a≠0)的对称轴为直 线 x=-2,与 x 轴的一个交点在(-3,0)和(-4,0)之间,∴另 一个交点位于(-1,0)和(0,0)之间,∴抛物线与 y 轴的交点在原点的下方,∴c<0.故②正确; ∵4a-b=0,∴b=4a. ∵抛物线 y=ax2+bx+c(a≠0)与 x 轴有两个交点, ∴Δ=b2-4ac=(4a)2-4ac=16a2-4ac>0.∵a<0,∴4a-c<0,∴c>4a,∴-3a+c>-3a+4a=a<0,故③错误; ∵4a-b=0,∴b=4a,∴at2+bt-(4a-2b)=at2+4at-(4a-2×4a)=at2+4at+4a=a(t2+4t+4)=a(t+2)2. ∵t 为实数,a<0,∴a(t+2)2≤0,∴at2+bt-(4a-2b)≤0,∴at2+bt≤4a-2b,即 4a-2b≥at2+bt,∴④错误; ∵点 - ,y1 , - ,y2 , - ,y3 是该抛物线上的点, ∴将它们描在图象上如图: 由图象可知:y1PF,∴PF<2PE,故②错误; 由翻折可知 EF⊥PB,∴∠EBQ=∠EFB=30°, ∴BE=2EQ,EF=2BE, ∴FQ=3EQ,故③错误; 由翻折的性质知,∠EFB=∠EFP=30°, ∴∠BFP=30°+30°=60°. ∵∠PBF=90°-∠EBQ=90°-30°=60°, ∴∠PBF=∠PFB=60°, ∴△PBF 是等边三角形,故④正确. 综上所述,结论正确的是①④. 4.C [ 解 析 ] 在 正 方 形 ABCD 中 ,∠A=90°. 由 △BPC 是 等 边 三 角 形 , 可 得 ∠CBP=60°,∴∠ABP=30°,∴BE =2AE,即①正确;BD 是正方形 ABCD 的对角线,可得△BCD 是 等腰直角三角形,∴∠CBD=∠CDB=45°,可得∠PBD=15°.∵CD=CP=CB,∠PCD=30°, 可得 ∠CPD=∠CDP=75°,∴∠BPD=75°+60°=135°,∠FDP=90°-75°=15°,∠PFD=90°-∠PCD=90° -30°=60 °,∠FPD=180°-∠PDF-∠PFD=180° -15°-60°=105°,∴∠PBD=∠PDF,∠BPH=∠DF P,∴△DFP∽△BPH, 即 ② 正 确 ;∠BPD≠∠DPF,∴③△PFD∽△PDB 错 误 ; 由 ∠PDH=∠PDC-∠CDB=75°-45°=30°=∠PCD,∠CPD=∠DPH, 可 得 △PDC∽△PHD,∴DP2=PH·PC,即④正确. 5.①②③ [解析] 由折叠的性质可知 CF=CB,∠CFE=90°,∠CEB=∠CEF,当 E 为 AB 中点 时 ,BE=EF=AE= ,∴∠FAE=∠AFE,∵∠FEB=∠FAE+∠AFE,∴∠CEB=∠CEF=∠FAE=∠A FE,∴AF∥CE,故①正确; ∵E 为 AB 中 点 时 ,BE = ,BC=2,∴CE= , 过 点 E 作 EM⊥AF 于 点 M,∵∠AFE=∠FEC,EM⊥AF,∠CFE=90°, ∴AF=2MF,△MFE∽△FEC,∴ = ,即 = ,∴MF= ,∴AF= ,故②正确; 当 A,F,C 三点共线时,∠AFE=90°,AC= = ,设 BE=x,则 EF=x,AE=3-x,AF= -2, 在 Rt△AFE 中,( -2)2+x2=(3-x)2,解得 x= ,∴AE=3-x= ,故③正确; ∵AF= -2,CF=2,∴AF≠CF,∴④错误. 6.①②③ [解析] ①∵ 正 方 形 的 各 边 相 等 , 各 角 都 是 90°,∴CB=CD,CE=CG,∠BCD=∠ECG=90°.∴∠BCD+∠DCE=∠ECG+∠DCE, 即 ∠BCE=∠DCG.∴△BCE≌△DCG(SAS),∴BE=DG.结论①正确. ②如图,设 BE 交 DC 于点 M,交 DG 于点 O.由△BCE≌△DCG 可知∠CBE=∠CDG. 又∠BMC=∠DMO,∴∠DOB=∠DCB=90°,即 BE⊥DG.结论②正确. ③ 连 接 BD,EG.∵BE⊥DG,∴DE2+BG2=(OD2+OE2)+(OB2+OG2)=(OD2+OB2)+(OE2+OG2)=BD2+EG2. 由勾股定理得 BD2+EG2=2a2+2b2.∴DE2+BG2=2a2+2b2.结论③正确. 综上所述,正确的结论是 ①②③. 单元测试卷(三) (考试时间:120 分钟 试卷满分:120 分) 一、选择题(每小题 3 分,共 36 分) 1.函数 y= 中,自变量 x 的取值范围是 ( ) A.x≥- B.x≥ C.x≤- D.x≤ 2.已知点 A(a,1)与点 B(-4,b)关于原点对称,则 a+b 的值为 ( ) A.5 B.-5 C.3 D.-3 3.若 k≠0,b<0,则 y=kx+b 的图象可能是图 D3-1 中的 ( ) 图 D3-1 4.如图 D3-2,在平面直角坐标系 xOy 中,函数 y=kx+b(k≠0)与 y= (m≠0)的图象相交于点 A(2,3),B(-6,-1),则不等式 kx+b> 的解集为 ( ) 图 D3-2 A.x<-6 B.-62 C.x>2 D.x<-6 或 00)的图象上,当 m>1 时, 过点 P 分别作 x 轴,y 轴的垂线,垂足分别为点 A,B;过点 Q 分别作 x 轴,y 轴的垂线,垂足分别 为点 C,D,QD 交 PA 于点 E,随着 m 的增大,四边形 ACQE 的面积 ( ) 图 D3-3 A.减小 B.增大 C.先减小后增大 D.先增大后减小 7.已知二次函数 y=ax2+bx+c(a≠0)的图象如图 D3-4 所示,则下列结论正确的是 ( ) 图 D3-4 A.a>0 B.c<0 C.3 是方程 ax2+bx+c=0 的一个根 D.当 x<1 时,y 随 x 的增大而减小 8.直线 y=x+1 与直线 y=-2x+a 的交点在第一象限,则 a 的取值可以是 ( ) A.-1 B.0 C.1 D.2 9.如果将抛物线 y=x2+2 向下平移 1 个单位,那么所得新抛物线的表达式是 ( ) A.y=(x-1)2+2 B.y=(x+1)2+2 C.y=x2+1 D.y=x2+3 10.已知点 P(m,n)是一次函数 y=x-1 的图象位于第一象限部分上的点,其中实数 m,n 满足 (m+2)2-4m+n(n+2m)=8,则点 P 的坐标为 ( ) A. ,- B. , C.(2,1) D. , 11.已知二次函数 y=-(x-1)2+5,当 m≤x≤n 且 mn<0 时,y 的最小值为 2m,最大值为 2n,则 m+n 的值为 ( ) A. B.2 C. D. 12.如图 D3-5,过点 A0(2,0)作直线 l:y= x 的垂线,垂足为点 A1,过点 A1 作 A1A2⊥x 轴,垂足为 点 A2,过点 A2 作 A2A3⊥l,垂足为点 A3,…,这样依次下去,得到一组线段:A0A1,A1A2,A2A3,…,则线 段 A2018A2019 的长为 ( ) 图 D3-5 A. B. C. D. 二、填空题(每小题 3 分,共 18 分) 13.若抛物线 y=ax2+bx+c 的开口向下,则 a 的值可能是 .(写一个即可) 14.如图 D3-6,反比例函数 y= 的图象经过矩形 OABC 的边 AB 的中点 D,则矩形 OABC 的面积 为 . 图 D3-6 15.若点 P(x-2,x+3)在第一象限,则 x 的取值范围是 . 16.如图 D3-7,在平面直角坐标系中,将点 P(-4,2)绕原点顺时针旋转 90°,则其对应点 Q 的 坐标为 . 图 D3-7 17.如图 D3-8,抛物线 y=ax2+bx+c 与 x 轴相交于点 A,B(m+2,0),与 y 轴相交于点 C,点 D 在该 抛物线上,坐标为(m,c),则点 A 的坐标是 . 图 D3-8 18.如图 D3-9①,E 为矩形 ABCD 的边 AD 上一点,点 P 从点 B 处出发沿折线 BE-ED-DC 运动到点 C 停止,点 Q 从点 B 处出发沿 BC 运动到点 C 停止,它们运动的速度都是 1 cm/s.若点 P、点 Q 同时开始运动,设运动时间为 t(s),△BPQ 的面积为 y(cm2),已知 y 与 t 之间的函数图象如图 D3-9②所示.给出下列结论:①当 018 时,y 关于 x 的函数表达式;若小敏家某月缴水费 81 元,则她家这个月的用水量 为多少立方米? 图 D3-12 22.(8 分)甲、乙两车分别从 A,B 两地同时出发.甲车匀速前往 B 地,到达 B 地立即以另一速 度按原路匀速返回到 A 地;乙车匀速前往 A 地.设甲、乙两车距 A 地的路程为 y(千米),甲车 行驶的时间为 x(时),y 与 x 之间的函数图象如图 D3-13 所示. 图 D3-13 (1)求甲车从 A地到达 B 地的行驶时间; (2)求甲车返回时 y 与 x 之间的函数关系式,并写出自变量 x 的取值范围; (3)求乙车到达 A 地时甲车距 A 地的路程. 23.(8 分)甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图 D3-14,甲 在 O 点正上方 1 m 的 P 处发出一球,羽毛球飞行的高度 y(m)与水平距离 x(m)之间满足函数表 达式 y=a(x-4)2+h.已知点 O 与球网的水平距离为 5 m,球网的高度为 1.55 m. 图 D3-14 (1)当 a=- 时,①求 h 的值;②通过计算判断此球能否过网. (2)若甲发球过网后,羽毛球飞行到与点 O 的水平距离为 7 m,离地面的高度为 m 的 Q 处时, 乙扣球成功,求 a 的值. 24.(10 分)如图 D3-15,一次函数 y=kx+b 的图象与反比例函数 y= 的图象在第一象限交于点 A(4,3),与 y 轴的负半轴交于点 B,且 OA=OB. 图 D3-15 (1)求函数 y=kx+b 和 y= 的表达式; (2)已知点 C(0,5),试在该一次函数图象上确定一点 M,使得 MB=MC,求此时点 M 的坐标. 25.(10 分)某公司开发出一款新的节能产品,该产品的成本价为 6 元/件,该产品在正式投放 市场前通过代销点进行了为期一个月(30 天)的试销售,售价为 8 元/件.工作人员对销售情况 进行了跟踪记录,并将记录情况绘制成图象,图 D3-16 中的折线 ODE 表示日销售量 y(件)与销 售时间 x(天)之间的函数关系.已知线段 DE 表示的函数关系中,时间每增加 1 天,日销售量减 少 5 件. 图 D3-16 (1)第 24 天的日销售量是 件,日销售利润是 元; (2)求 y 与 x 之间的函数关系式,并写出 x 的取值范围; (3)日销售利润不低于 640 元的天数共有多少天?试销售期间,日销售最大利润是多少元? 26.(10 分)如图D3-17,已知抛物线 y= x2- x-n(n>0)与 x 轴交于 A,B 两点(A 点在 B 点的左边), 与 y 轴交于点 C. 图 D3-17 (1)如图①,若△ABC 为直角三角形,求 n 的值; (2)如图①,在(1)的条件下,点 P 在抛物线上,点 Q 在抛物线的对称轴上,若以 BC 为边,以点 B,C,P,Q 为顶点的四边形是平行四边形,求 P 点的坐标; (3)如图②,过点 A 作直线 BC 的平行线交抛物线于另一点 D,交 y 轴于点 E,若 AE∶ED=1∶4, 求 n 的值. 参考答案 1.B 2.C 3.B 4.B 5.D 6.B 7.C 8.D 9.C 10.D 11.D [解析] 结合二次函数图象的开口方向、对称轴以及增减性进行解答即可. 二次函数 y=-(x-1)2+5 的大致图象如下: 因为 mn<0,所以 m<0,n>0. (1)当 n<1 时,在 x=m 处 y 取最小值,即 2m=-(m-1)2+5, 解得 m=-2(m=2 不合题意,舍去). 在 x=n 处y 取最大值,即 2n=-(n-1)2+5, 解得 n=2 或 n=-2(均不合题意,舍去). (2)当 n≥1 时, 在 x=1 处 y 取最大值,即 2n=-(1-1)2+5, 解得 n= . ①当 m<- 时, 在 x=m 处 y 取最小值,即 2m=-(m-1)2+5,解得 m=-2. 所以 m+n= . ②当 0>m≥- 时,在 x=n,即 n= 处 y 取最小值, 即 2m=- -1 2+5. 解得 m= (舍去). 所以 m+n=-2+ = . 故选 D. 12.B [解析] 由 y= x 可得该直线与 x 轴的正方向的夹角∠A0OA1=30°, 由已知,可得∠A0A1A2=∠A1A2A3=∠A2A3A4=∠A3A4A5=∠A4A5A6=30°, ∴在 Rt△A0A1O 中,A0A1= OA0= ×2=1,A1A2=A0A1·cos 30°= , 同理可得 A2A3=A1A2·cos 30°= 2, A3A4=A2A3·cos 30°= 3,…, 以此类推,可得 A2018A2019= 2018. 13.-1(答案不唯一,小于零即可) 14.4 15.x>2 16.(2,4) 17.(-2,0) [解析] 根据函数值相等的两点关于对称轴对称可得对称轴,根据 A,B 关于对称轴 对称,可得点 A 的坐标. 由 C(0,c),D(m,c),得函数图象的对称轴是直线 x= . 设点 A 的坐标为(x,0),由 A,B 关于对称轴 x= 对称,得 = . 解得 x=-2, 即点 A 的坐标为(-2,0). 故答案为(-2,0). 18.①③⑤ [解析] 由题图②可判断出 BE=BC=10 cm,DE=4 cm.当点 P 在 ED 上运动 时,S△BPQ=40 cm2,∴AB=8 cm,∴AE=6 cm.∴当 00). 在直线 y=2x-6 上,当 y=0 时,x=3, ∴点 C 的坐标为(3,0),即 OC=3. ∴S△POC= OC·yP= ×3× =9. 解得 n= . ∴点 P 的坐标为 ,6 . 故当 S△POC=9 时,在第一象限内,反比例函数 y= 的图象上点 P 的坐标为 ,6 . 21.解:(1)设函数表达式为 y=ax(x≤18). ∵直线 y=ax 过点(18,45),∴18a=45.解得 a= .∴y= x(x≤18).将 x=16 代入,得 y=40. 答:应缴水费 40 元. (2)设函数表达式为 y=kx+b(x>18). ∵直线 y=kx+b 过点(18,45),(28,75), ∴ 解得 ∴y=3x-9(x>18). 由 81 元>45 元,得用水量超过 18 立方米. ∴当 y=81 时,3x-9=81, 解得 x=30. 答:她家这个月的用水量为 30 立方米. 22.解:(1)180÷1.5=120(千米/时), 300÷120=2.5(小时). 答:甲车从 A 地到达 B 地行驶了 2.5 小时. (2)设所求函数关系式为 y=kx+b(k≠0).将(2.5,300),(5.5,0)分别代入,得 解得 ∴y=-100x+550(2.5≤x≤5.5). (3)(300-180)÷1.5=80(千米/时), 300÷80=3.75(时). 当 x=3.75 时,y 甲=175. 答:乙车到达 A 地时,甲车距离 A 地 175 千米. 23.解:(1)①把(0,1),a=- 代入 y=a(x-4)2+h,得 1=- ×16+h.解得 h= . ②把 x=5 代入 y=- (x-4)2+ ,得 y=- (5-4)2+ =1.625. ∵1.625>1.55,∴此球能过网. (2)把点(0,1), 7, 分别代入 y=a(x-4)2+h,得 解得 ∴a=- . 24.[解析] (1)利用待定系数法即可解答; (2)设点 M 的坐标为(x,2x-5),根据 MB=MC,得到 = ,即可解答. 解:(1)把 A(4,3)的坐标代入 y= ,得 a=3×4=12.∴y= . 易得 OA= =5. ∵OA=OB,∴OB=5. ∴点 B 的坐标为(0,-5). 把 B(0,-5),A(4,3)的坐标分别代入 y=kx+b,得 解得 ∴y=2x-5. (2)∵点 M 在一次函数 y=2x-5 的图象上, ∴设点 M 的坐标为(x,2x-5). ∵MB=MC, ∴ = . 解得 x=2.5. ∴点 M 的坐标为(2.5,0). 25.解:(1)330 660 (2)设线段 OD 所表示的 y 与 x 之间的函数解析式为 y=kx. ∵y=kx 的图象过点(17,340),∴17k=340. 解得 k=20. ∴线段 OD 所表示的 y 与 x 之间的函数解析式为 y=20x. 由题意得,线段 DE 所表示的 y 与 x 之间的函数解析式为 y=340-5(x-22)=-5x+450. ∵D 是线段 OD 与线段 DE 的交点, 解方程组 得 ∴点 D 的坐标为(18,360). ∴y= (3)当 0≤x≤18 时,由题意,得(8-6)×20x≥640,解得 x≥16; 当 180),可得 OC=n,OA·OB=2n, ∴n2=2n,解得:n1=2,n2=0(舍去), ∴n=2. (2)由(1)可知抛物线的对称轴为直线 x= ,抛物线解析式为 y= x2- x-2,令 y=0,得 x1=-1,x2=4, ∴A(-1,0),B(4,0), 设点 P m, m2- m-2 , ①当直线 PQ∥BC 时,当点 P1 在点 Q1 的左侧时(如图①所示), 当 △BOC 平 移 到 △Q1NP1 的 位 置 时 , 四 边 形 P1Q1BC 为 平 行 四 边 形 , 此 时 NQ1=OB, 即 -m=4,m=- . 当 m=- 时,y= m2- m-2= ,此时点 P 的坐标为 - , . 当点 P2 在点 Q2 的右侧时(如图①所示), 同理可得:m- =4,m= . 当 m= 时,y= m2- m-2= ,此时点 P 的坐标为 , . ②当直线 PQ 与直线 BC 相交时,如图②所示: 此时点 P 到 y 轴的距离等于点 B 到对称轴的距离. 即 m=4- = . 当 m= 时,y= m2- m-2=- ,此时点 P 的坐标为 ,- . 综上所述,满足条件的点 P 的坐标为 - , , , , ,- . (3)如图③,过点 D 作 DF⊥x 轴,垂足为 F. 则 AO∶OF=AE∶ED=1∶4. 设 A(a,0),B(b,0), 则 AO=-a,OF=-4a, ∵AD∥BC, ∴∠DAO=∠OBC, ∵∠AFD=∠BOC=90°, ∴△BOC∽△AFD, ∴ = , 即 = , 由题意:ab=-2n,∴ =- , ∴DF=-5a· =-5a· - = a2, ∵点 A,D 在抛物线上, ∴ 解得: ∴n 的值为 . - 初中毕业生学业考试 数 学 本试卷分选择题和非选择题两部分,共三大题 25 小题,满 150 分。考试用时 120 分钟。 注意事项： 1. 答卷前，考生务必在答题卡第 1 面、第 3 面、第 5 面上用黑色字迹的钢 笔或签字笔填写自己的考生号、姓名；填写考点考场号、座位号，再用 2B 铅笔把对应这两个号码的标号涂黑。 2. 选择题每小题选出答案后，用 2B 铅笔把答题卡上对应题目的答题标号 涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号；不能答在试 卷上。 3. 非选择题必须用黑色字迹的钢笔或签字笔作答，涉及作图的题目，用 2B 铅笔画图。答案必须写在答题卡各题目指定区域内的相应位置上； 如需改动，先划掉原来的答案，然后再写上新的答案；改动的答案也不 能超出指定的区域，不准使用铅笔、圆珠笔和涂改液，不按以上要求作 答的答案无效。 4. 考生必须保持答题卡的整洁，考试结束后，将本试卷和答题卡一并交回。 第一部分 选择题（共 30 分） 一、 选择题 （本大题共 10 小题，每小题 3 分，满分 30 分.在每小题给出的四个选项中，只 有一项是符合题目要求的.） 1．四个数 0，1， ， 中，无理数的是( ) （A） （B）1 （C） （D）0 2．图 1 所示的五角星是轴对称图形，它的对称轴共有( ) （A）1 条 （B）3 条 （C）5 条 （D）无数条 3．图 2 所示的几何体是由 4 个相同的小正方体搭成的，它的主视图是( ) 4．下列计算正确的是( ) （A）(a + b)2 = a2 + b2 （B）a2 +2 a2 = 3a4 （C）x2y ÷ = x2 (y ≠ 0) （D）(-2 x2)3 = -8 x6 5．如图 3，直线 AD，BE 被直线 BF 和 AC 所截， 则∠1 同位角和∠5 的内错角分别是 （A）∠4，∠2 （B）∠2，∠6 （C）∠5，∠4 （D）∠2，∠4 6．甲袋中装有 2 个相同的小球，分别写有数字 1 和 2；乙袋中装有 2 个相同的 小球，分别写有数字 1 和 2，从两个口袋中各随机取出 1 个小球，取出的两个小球上都 写有数字 2 的概率是( ) （A） （B） （C） （D） 7．如图 4，AB 是 ʘ O 的弦，OC⊥AB，交 ʘ O 于点 C，连接 OA，OB， BC，若∠ABC=20°，则∠AOB 的度数是( ) （A）40° （B）50° （C）70° （D）80° 8． 《九章算术》是我国古代数字的经典著作，书中有一个问题：“今有黄金九枚，白 银一十一枚，称之重适等。交易其一，金轻十三两，问金、银一枚各重几何？”.意 思是：甲袋中装有黄金 9 枚（每枚黄金重量相同），乙袋中装有白银 11 枚（每枚白 银重量相同），称重两袋相等.两袋互相交换 1 枚后，甲袋比乙袋轻了 13 两（袋子 重量忽略不计）.问黄金、白银每枚各重多少两？设每枚黄金重 x 两，每枚白银重 y 两，根据题意得：( ) 9．一次函数 y  ax b 和反比例函数 y a  b 在同一直角坐标系中的大致图像（ ） x 是( ) 10．在平面直角坐标系中，一个智能机器人接到如下指令：从原点 O 出发，按向右，向上， 向右，向下的方向依次不断移动，每次移动 1m，其行走路线如图 5 所示，第一次移动 到 A1 ，第二次移动到 A2，…，第 n 次移动到 An，则 △ OA2A2018 的面积是( ) （A）504m2 （B） m2 （C） m2 （D）1009m2 第二部分 非选择题（共 120 分） 二、填空题（本大题共 6 小题，每小题 3 分，满分 18 分.） 11．已知二次函数 y=x2，当 x＞0 时，y 随 x 的增大而______（填“增大”或“减小”）． 12．如图 6，旗杆高 AB  8m ，某一时刻，旗杆影子长 BC 16m， 则 tanC ______． 13. 方程 = 的解是 _________. 14．如图 7，若菱形 ABCD 的顶点 A，B 的 坐标分别为（3,0），（﹣2，0），点 D 在 y 轴上，则点 C 的坐标是_________. 15．如图 8，数轴上点 A 表示的数为 a， 化简：a + = _________. 16．如图 9，CE 是▱ ABCD 的边 AB 的垂直平分线，垂足为点 O，CE 与 DA 的延长线交于 点 E，连接 AC， BE，DO，DO 与 AC 交于点 F，则下列结论： ①四边形 ACBE 是菱形；②∠ACD =∠BAE ； ③ AF: BE = 2:3；④S 四边形 AFOE : S△COD = 2:3． 其中正确的结论有__________．（填写所有正确结论的序号） 三、解答题（本大题共 9 小题，满分 102 分，解答应写出文字说明、证明过程或演算步骤）． 17．（本小题满分 9 分） 解不等式组： 18．（本小题满分 9 分） 如图 10，AB 与 CD 相交与点 E，AE = CE，DE = BE，求证： ∠A =∠C 19．（本小题满分 10 分） 20．（本小题满分 10 分） 随着移动互联网的快速发展，基于互联网的共享单车应运而生，为了解某小区居民使用 共享单车的情况，某研究小组随机采访该小区的 10 位居民，得到这 10 位居民一周内使 用共享单车的次数分别为：17，12，15，20，17，0，7，26，17，9． （1）这组数据的中位数是__________，众数是__________． （2）计算这 10 位居民一周内使用共享单车的平均次数． （3）若该小区 200 名居民，试估计该小区一周内使用共享单车的总次数． 21．（本小题满分 12 分） 友谊商店 A 型号笔记本电脑售价是 a 元/台，最近，该商店对 A 型号笔记本电脑举行 促销活动，有两种优惠方案，方案一：每台按售价的九折销售；方案二：若购买不超过 5 台，每台按售价销售；若超过 5 台，超过部分每台按售价的八折销售．某公司一次性 从友谊商店购买 A 型号笔记本电脑 x 台． （1）当 x = 8 时，应选择哪种方案，该公司购买费用最少？最少费用是多少元？ （2）若该公司采用方案二购买更合算，求 x 的取值范围. 22.（本小题满分 12 分） 设 P (x ,0) 是 x 轴上的一个动点，它与原点的距离为 y1 ． （1）求 y1 关于 x 的函数解析式，并画出这个函数的图象． （2）若反比例函数 y2 = 的图象与函数 y1 的图象相交于点 A，且点 A 的纵坐标为 2． ①求 k 值． ②结合图象，当 y1＞y2 时，写出 x 的取值范围. 23、（本小题满分 12 分） 如图 11，在四边形 ABCD 中， ∠ B = ∠C = 90 ゜，AB ＞ CD, AD = AB + CD． （1）利用尺规作 ∠ADC 的平分线 DE，交 BC 于点 E ． （2）在（1）的条件下． ①证明：AE⊥DE ． ②若 CD = 2，AB = 4，点 M，N 分别是 AE，AB 上的动点，求 BM + MN 的最小值． 24．（本小题满分 14 分） 已知抛物线 y=x2 + mx – 2m – 4 (m＞0) （1）证明：该抛物线与 x 轴总有两个不同的交点． （2）设该抛物线与 x 轴的两个交点分别为 A，B（点 A 在点 B 的右侧），与 y 轴交于点 C， A，B，C 三点都在⊙P 上． ①试判断：不论 m 取任何正数，⊙P 是否经过 y 轴上某个定点？若是，求出该定点的 坐标；若不是，说明理由． ②若点 C 关于直线 x = – 的对称点为点 E，点 D (0,1) ，连接 BE，BD， DE， △BDE 的周长记为 l，⊙P 的半径记为 r，求 的值． 25．（本小题满分 14 分） 如图 12，在四边形 ABCD 中，∠B= 60 ゜，∠D =30 ゜，AB = BC （1）求 ∠A +∠C 的度数； （2）连接 BD，探究 AD，BD，CD 三者之间的数量关系，并说明理由； （3）若 AB =1，点 E 在四边形 ABCD 内部运动，且满足 AE2 = BE2 + CE2，求点 E 的运动 路径的长度. 参考答案： 一、选择题 1.A 2.C 3.B 4.D 5.B 6.C 7.D 8.D 9.A 10.A 二、填空题 11. 增大 12. 13. x = 2 14. (-5,4) 15. 2 16. ①②④ 三、解答题 17. 解： 18. 证： 19. 解： 20. 解： 21. 解： 22. 解： 23. （1）如图： 24. 证： 25. 解： 中考数学试卷 一、选择题（以下每个小题均有 A、B、C、D 四个选项.其中只有一个选项正确. 请用 2B 铅笔在答题卡相应位置作答.每题 3 分.共 30 分） 1．（3.00 分）（2018•贵阳）当 x=﹣1 时，代数式 3x+1 地值是（ ） A．﹣1 B．﹣2 C．4 D．﹣4 2．（3.00 分）（2018•贵阳）如图，在△ABC 中有四条线段 DE，BE，EF，FG，其 中有一条线段是△ABC 地中线，则该线段是（ ）b5E2RGbCAP A．线段 DE B．线段 BE C．线段 EF D．线段 FG 3．（3.00 分）（2018•贵阳）如图是一个几何体地主视图和俯视图，则这个几何体 是（ ） A．三棱柱 B．正方体 C．三棱锥 D．长方体 4．（3.00 分）（2018•贵阳）在“生命安全”主题教育活动中，为了解甲、乙、丙、 丁四所学校学生对生命安全知识掌握情况，小丽制定了如下方案，你认为最合理 地是（ ）p1EanqFDPw A．抽取乙校初二年级学生进行调查 B．在丙校随机抽取 600 名学生进行调查 C．随机抽取 150 名老师进行调查 D．在四个学校各随机抽取 150 名学生进行调査 5．（3.00 分）（2018•贵阳）如图，在菱形 ABCD 中，E 是 AC 地中点，EF∥CB， 交 AB 于点 F，如果 EF=3，那么菱形 ABCD 地周长为（ ）DXDiTa9E3d A．24 B．18 C．12 D．9 6．（3.00 分）（2018•贵阳）如图，数轴上有三个点 A、B、C，若点 A、B 表示地 数互为相反数，则图中点 C 对应地数是（ ）RTCrpUDGiT A．﹣2 B．0 C．1 D．4 7．（3.00 分）（2018•贵阳）如图，A、B、C 是小正方形地顶点，且每个小正方形 地边长为 1，则 tan∠BAC 地值为（ ）5PCzVD7HxA A． B．1 C． D． 8．（3.00 分）（2018•贵阳）如图，小颖在围棋盘上两个格子地格点上任意摆放黑、 白两个棋子，且两个棋子不在同一条网格线上，其中，恰好摆放成如图所示位置 地概率是（ ）jLBHrnAILg A． B． C． D． 9．（3.00 分）（2018•贵阳）一次函数 y=kx﹣1 地图象经过点 P，且 y 地值随 x 值 地增大而增大，则点 P 地坐标可以为（ ）xHAQX74J0X A．（﹣5，3） B．（1，﹣3） C．（2，2） D．（5，﹣1） 10．（3.00 分）（2018•贵阳）已知二次函数 y=﹣x2+x+6 及一次函数 y=﹣x+m，将 该二次函数在 x 轴上方地图象沿 x 轴翻折到 x 轴下方，图象地其余部分不变，得 到一个新函数（如图所示），请你在图中画出这个新图象，当直线 y=﹣x+m 与新 图象有 4 个交点时，m 地取值范围是（ ）LDAYtRyKfE A．﹣ ＜m＜3B．﹣ ＜m＜2C．﹣2＜m＜3 D．﹣6＜m＜﹣2 二、填空題（每小题 4 分，共 20 分） 11．（4.00 分）（2018•贵阳）某班 50 名学生在 2018 年适应性考试中，数学成绩 在 100〜110 分这个分数段地频率为 0.2，则该班在这个分数段地学生为 人．Zzz6ZB2Ltk 12．（4.00 分）（2018•贵阳）如图，过 x 轴上任意一点 P 作 y 轴地平行线，分别 与反比例函数 y= （x＞0），y=﹣ （x＞0）地图象交于 A 点和 B 点，若 C 为 y 轴 任意一点．连接 AB、BC，则△ABC 地面积为．dvzfvkwMI1 13．（4.00 分）（2018•贵阳）如图，点 M、N 分别是正五边形 ABCDE 地两边 AB、 BC 上地点．且 AM=BN，点 O 是正五边形地中心，则∠MON 地度数是度．rqyn14ZNXI 14．（4.00 分）（2018•贵阳）已知关于 x 地不等式组 无解，则 a 地 取值范围是．EmxvxOtOco 15．（4.00 分）（2018•贵阳）如图，在△ABC 中，BC=6，BC 边上地高为 4，在△ ABC 地内部作一个矩形 EFGH，使 EF 在 BC 边上，另外两个顶点分别在 AB、AC 边上，则对角线 EG 长地最小值为．SixE2yXPq5 三、解答題(本大題 10 个小题，共 100 分） 16．（10.00 分）（2018•贵阳）在 6.26 国际禁毒日到来之际，贵阳市教育局为了 普及禁毒知识，提高禁毒意识，举办了“关爱生命，拒绝毒品”地知识竞赛．某校 初一、初二年级分别有 300 人，现从中各随机抽取 20 名同学地测试成绩进行调 查分折，成绩如下：6ewMyirQFL 初一： 68 88 100 100 79 94 89 85 100 88 100 90 98 97 77 94 96 100 92 67 初二： 69 97 91 69 98 100 99 100 90 100 99 69 97 100 99 94 79 99 98 79 （1）根据上述数据，将下列表格补充完成． 整理、描述数据： 分数段 60≤x≤69 70≤x≤79 80≤x≤89 90≤x≤100 初一人数 2 2 4 12 初二人数 2 2 1 15 分析数据：样本数据地平均数、中位数、满分率如表： 年级 平均教 中位教 满分率 初一 90.1 93 25% 初二 92.8 20% 得出结论： （2）估计该校初一、初二年级学生在本次测试成绩中可以得到满分地人数共人； （3）你认为哪个年级掌握禁毒知识地总体水平较好，说明理由． 17．（8.00 分）（2018•贵阳）如图，将边长为 m 地正方形纸板沿虚线剪成两个小 正方形和两个矩形，拿掉边长为 n 地小正方形纸板后，将剩下地三块拼成新地矩 形．kavU42VRUs （1）用含 m 或 n 地代数式表示拼成矩形地周长； （2）m=7，n=4，求拼成矩形地面积． 18．（8.00 分）（2018•贵阳）如图①，在 Rt△ABC 中，以下是小亮探究 与 之间关系地方法：y6v3ALoS89 ∵sinA= ，sinB= ∴c= ，c= ∴ = 根据你掌握地三角函数知识．在图②地锐角△ABC 中，探究 、 、 之 间地关系，并写出探究过程．M2ub6vSTnP 19．（10.00 分）（2018•贵阳）某青春党支部在精准扶贫活动中，给结对帮扶地贫 困家庭赠送甲、乙两种树苗让其栽种．已知乙种树苗地价格比甲种树苗贵 10 元， 用 480 元 购 买 乙 种 树 苗 地 棵 数 恰 好 与 用 360 元 购 买 甲 种 树 苗 地 棵 数 相 同．0YujCfmUCw （1）求甲、乙两种树苗每棵地价格各是多少元？ （2）在实际帮扶中，他们决定再次购买甲、乙两种树苗共 50 棵，此时，甲种树 苗地售价比第一次购买时降低了 10%，乙种树苗地售价不变，如果再次购买两种 树苗地总费用不超过 1500 元，那么他们最多可购买多少棵乙种树苗？eUts8ZQVRd 20．（10.00 分）（2018•贵阳）如图，在平行四边形 ABCD 中，AE 是 BC 边上地高， 点 F 是 DE 地中点，AB 与 AG 关于 AE 对称，AE 与 AF 关于 AG 对称．sQsAEJkW5T （1）求证：△AEF 是等边三角形； （2）若 AB=2，求△AFD 地面积． 21．（10.00 分）（2018•贵阳）图①是一枚质地均匀地正四面体形状地骰子，每个 面上分别标有数字 1，2，3，4，图②是一个正六边形棋盘，现通过掷骰子地方 式玩跳棋游戏，规则是：将这枚骰子掷出后，看骰子向上三个面（除底面外）地 数字之和是几，就从图②中地 A 点开始沿着顺时针方向连续跳动几个顶点，第二 次从第一次地终点处开始，按第一次地方法跳动．GMsIasNXkA （1）达机掷一次骰子，则棋子跳动到点 C 处地概率是 （2）随机掷两次骰子，用画树状图或列表地方法，求棋子最终跳动到点 C 处地 概率． 22．（10.00 分）（2018•贵阳）六盘水市梅花山国际滑雪自建成以来，吸引大批滑 雪爱好者，一滑雪者从山坡滑下，测得滑行距离 y（单位：cm）与滑行时间 x（单 位：s）之间地关系可以近似地用二次函数来表示．TIrRGchYzg 滑行时间 x/s 0 1 2 3 … 滑行距离 y/cm 0 4 12 24 … （1）根据表中数据求出二次函数地表达式．现测量出滑雪者地出发点与终点地 距离大约 800m，他需要多少时间才能到达终点？7EqZcWLZNX （2）将得到地二次函数图象补充完整后，向左平移 2 个单位，再向上平移 5 个 单位，求平移后地函数表达式． 23．（10.00 分）（2018•贵阳）如图，AB 为⊙O 地直径，且 AB=4，点 C 在半圆上， OC⊥AB，垂足为点 O，P 为半圆上任意一点，过 P 点作 PE⊥OC 于点 E，设△OPE 地内心为 M，连接 OM、PM．lzq7IGf02E （1）求∠OMP 地度数； （2）当点 P 在半圆上从点 B 运动到点 A 时，求内心 M 所经过地路径长． 24．（12.00 分）（2018•贵阳）如图，在矩形 ABCD 中，AB═2，AD= ，P 是 BC 边上地一点，且 BP=2CP．zvpgeqJ1hk （1）用尺规在图①中作出 CD 边上地中点 E，连接 AE、BE（保留作图痕迹，不 写作法）； （2）如图②，在（1）地条体下，判断 EB 是否平分∠AEC，并说明理由； （3）如图③，在（2）地条件下，连接 EP 并廷长交 AB 地廷长线于点 F，连接 AP，不添加辅助线，△PFB 能否由都经过 P 点地两次变换与△PAE 组成一个等腰 三角形？如果能，说明理由，并写出两种方法（指出对称轴、旋转中心、旋转方 向和平移距离）NrpoJac3v1 25．（12.00 分）（2018•贵阳）如图，在平面直角坐标系 xOy 中，点 A 是反比例 函数 y= （x＞0，m＞1）图象上一点，点 A 地横坐标为 m，点 B（0，﹣m） 是 y 轴负半轴上地一点，连接 AB，AC⊥AB，交 y 轴于点 C，延长 CA 到点 D，使 得 AD=AC，过点 A 作 AE 平行于 x 轴，过点 D 作 y 轴平行线交 AE 于点 E．1nowfTG4KI （1）当 m=3 时，求点 A 地坐标； （2）DE=，设点 D 地坐标为（x，y），求 y 关于 x 地函数关系式和自变量地取值 范围； （3）连接 BD，过点 A 作 BD 地平行线，与（2）中地函数图象交于点 F，当 m 为何值时，以 A、B、D、F 为顶点地四边形是平行四边形？fjnFLDa5Zo 参考答案与试题解析 一、选择题（以下每个小题均有 A、B、C、D 四个选项.其中只有一个选项正确. 请用 2B 铅笔在答题卡相应位置作答.每题 3 分.共 30 分）tfnNhnE6e5 1．（3.00 分）（2018•贵阳）当 x=﹣1 时，代数式 3x+1 地值是（ ） A．﹣1 B．﹣2 C．4 D．﹣4 【考点】33：代数式求值． 【专题】11 ：计算题． 【分析】把 x 地值代入解答即可． 【解答】解：把 x=﹣1 代入 3x+1=﹣3+1=﹣2， 故选：B． 【点评】此题考查了代数式求值，熟练掌握运算法则是解本题地关键． 2．（3.00 分）（2018•贵阳）如图，在△ABC 中有四条线段 DE，BE，EF，FG，其 中有一条线段是△ABC 地中线，则该线段是（ ）HbmVN777sL A．线段 DE B．线段 BE C．线段 EF D．线段 FG 【考点】K2：三角形地角平分线、中线和高． 【专题】1 ：常规题型；552：三角形． 【分析】根据三角形一边地中点与此边所对顶点地连线叫做三角形地中线逐一判 断即可得． 【解答】解：根据三角形中线地定义知线段 BE 是△ABC 地中线， 故选：B． 【点评】本题主要考查三角形地中线，解题地关键是掌握三角形一边地中点与此 边所对顶点地连线叫做三角形地中线．V7l4jRB8Hs 3．（3.00 分）（2018•贵阳）如图是一个几何体地主视图和俯视图，则这个几何体 是（ ） A．三棱柱 B．正方体 C．三棱锥 D．长方体 【考点】U3：由三视图判断几何体． 【专题】55：几何图形． 【分析】根据三视图得出几何体为三棱柱即可． 【解答】解：由主视图和俯视图可得几何体为三棱柱， 故选：A． 【点评】本题考点是简单空间图形地三视图，考查根据作三视图地规则来作出三 个视图地能力，三视图地投影规则是：“主视、俯视长对正；主视、左视高平齐， 左视、俯视宽相等”．三视图是高考地新增考点，不时出现在高考试题中，应予 以重视．83lcPA59W9 4．（3.00 分）（2018•贵阳）在“生命安全”主题教育活动中，为了解甲、乙、丙、 丁四所学校学生对生命安全知识掌握情况，小丽制定了如下方案，你认为最合理 地是（ ）mZkklkzaaP A．抽取乙校初二年级学生进行调查 B．在丙校随机抽取 600 名学生进行调查 C．随机抽取 150 名老师进行调查 D．在四个学校各随机抽取 150 名学生进行调査 【考点】V2：全面调查与抽样调查． 【专题】54：统计与概率． 【分析】根据抽样调查地具体性和代表性解答即可． 【解答】解：为了解甲、乙、丙、丁四所学校学生对生命安全知识掌握情况，在 四个学校各随机抽取 150 名学生进行调査最具有具体性和代表性，AVktR43bpw 故选：D． 【点评】此题考查抽样调查，关键是理解抽样调查地具体性和代表性． 5．（3.00 分）（2018•贵阳）如图，在菱形 ABCD 中，E 是 AC 地中点，EF∥CB， 交 AB 于点 F，如果 EF=3，那么菱形 ABCD 地周长为（ ）ORjBnOwcEd A．24 B．18 C．12 D．9 【考点】KX：三角形中位线定理；L8：菱形地性质． 【专题】1 ：常规题型；556：矩形菱形正方形． 【分析】易得 BC 长为 EF 长地 2 倍，那么菱形 ABCD 地周长=4BC 问题得解． 【解答】解：∵E 是 AC 中点， ∵EF∥BC，交 AB 于点 F， ∴EF 是△ABC 地中位线， ∴EF= BC， ∴BC=6， ∴菱形 ABCD 地周长是 4×6=24． 故选：A． 【点评】本题考查地是三角形中位线地性质及菱形地周长公式，题目比较简单． 6．（3.00 分）（2018•贵阳）如图，数轴上有三个点 A、B、C，若点 A、B 表示地 数互为相反数，则图中点 C 对应地数是（ ）2MiJTy0dTT A．﹣2 B．0 C．1 D．4 【考点】13：数轴；14：相反数． 【专题】1 ：常规题型． 【分析】首先确定原点位置，进而可得 C 点对应地数． 【解答】解：∵点 A、B 表示地数互为相反数， ∴原点在线段 AB 地中点处， ∴点 C 对应地数是 1， 故选：C． 【点评】此题主要考查了数轴，关键是正确确定原点位置． 7．（3.00 分）（2018•贵阳）如图，A、B、C 是小正方形地顶点，且每个小正方形 地边长为 1，则 tan∠BAC 地值为（ ）gIiSpiue7A A． B．1 C． D． 【考点】KQ：勾股定理；T1：锐角三角函数地定义；T7：解直角三角形． 【专题】554：等腰三角形与直角三角形． 【分析】连接 BC，由网格求出 AB，BC，AC 地长，利用勾股定理地逆定理得到 △ABC 为等腰直角三角形，即可求出所求．uEh0U1Yfmh 【解答】解：连接 BC， 由网格可得 AB=BC= ，AC= ，即 AB2+BC2=AC2， ∴△ABC 为等腰直角三角形， ∴∠BAC=45°， 则 tan∠BAC=1， 故选：B． 【点评】此题考查了锐角三角函数地定义，解直角三角形，以及勾股定理，熟练 掌握勾股定理是解本题地关键． 8．（3.00 分）（2018•贵阳）如图，小颖在围棋盘上两个格子地格点上任意摆放黑、 白两个棋子，且两个棋子不在同一条网格线上，其中，恰好摆放成如图所示位置 地概率是（ ）IAg9qLsgBX A． B． C． D． 【考点】X6：列表法与树状图法． 【专题】1 ：常规题型． 【分析】先找出符合地所有情况，再得出选项即可． 【解答】解：恰好摆放成如图所示位置地概率是 = ， 故选：D． 【点评】本题考查了列表法与树形图法，能找出符合地所有情况是解此题地关键． 9．（3.00 分）（2018•贵阳）一次函数 y=kx﹣1 地图象经过点 P，且 y 地值随 x 值 地增大而增大，则点 P 地坐标可以为（ ）WwghWvVhPE A．（﹣5，3） B．（1，﹣3） C．（2，2） D．（5，﹣1） 【考点】F5：一次函数地性质；F8：一次函数图象上点地坐标特征． 【专题】33 ：函数思想． 【分析】根据函数图象地性质判断系数 k＞0，则该函数图象经过第一、三象限， 由函数图象与 y 轴交于负半轴，则该函数图象经过第一、三、四象限，由此得到 结论．asfpsfpi4k 【解答】解：∵一次函数 y=kx﹣1 地图象地 y 地值随 x 值地增大而增大， ∴k＞0， A、把点（﹣5，3）代入 y=kx﹣1 得到：k=﹣ ＜0，不符合题意； B、把点（1，﹣3）代入 y=kx﹣1 得到：k=﹣2＜0，不符合题意； C、把点（2，2）代入 y=kx﹣1 得到：k= ＞0，符合题意； D、把点（5，﹣1）代入 y=kx﹣1 得到：k=0，不符合题意； 故选：C． 【点评】考查了一次函数图象上点地坐标特征，一次函数地性质，根据题意求得 k＞0 是解题地关键． 10．（3.00 分）（2018•贵阳）已知二次函数 y=﹣x2+x+6 及一次函数 y=﹣x+m，将 该二次函数在 x 轴上方地图象沿 x 轴翻折到 x 轴下方，图象地其余部分不变，得 到一个新函数（如图所示），请你在图中画出这个新图象，当直线 y=﹣x+m 与新 图象有 4 个交点时，m 地取值范围是（ ）ooeyYZTjj1 A．﹣ ＜m＜3B．﹣ ＜m＜2C．﹣2＜m＜3 D．﹣6＜m＜﹣2 【考点】F7：一次函数图象与系数地关系；H6：二次函数图象与几何变换；HA： 抛物线与 x 轴地交点． 【专题】31 ：数形结合． 【分析】如图，解方程﹣x2+x+6=0 得 A（﹣2，0），B（3，0），再利用折叠地性 质求出折叠部分地解析式为 y=（x+2）（x﹣3），即 y=x2﹣x﹣6（﹣2≤x≤3），然 后求出直线•y=﹣x+m 经过点 A（﹣2，0）时 m 地值和当直线 y=﹣x+m 与抛物线 y=x2﹣x﹣6（﹣2≤x≤3）有唯一公共点时 m 地值，从而得到当直线 y=﹣x+m 与 新图象有 4 个交点时，m 地取值范围．BkeGuInkxI 【解答】解：如图，当 y=0 时，﹣x2+x+6=0，解得 x1=﹣2，x2=3，则 A（﹣2，0）， B（3，0），PgdO0sRlMo 将该二次函数在 x 轴上方地图象沿 x 轴翻折到 x 轴下方地部分图象地解析式为 y= （x+2）（x﹣3）， 即 y=x2﹣x﹣6（﹣2≤x≤3）， 当直线•y=﹣x+m 经过点 A（﹣2，0）时，2+m=0，解得 m=﹣2； 当直线 y=﹣x+m 与抛物线 y=x2﹣x﹣6（﹣2≤x≤3）有唯一公共点时，方程 x2﹣x ﹣6=﹣x+m 有相等地实数解，解得 m=﹣6，3cdXwckm15 所以当直线 y=﹣x+m 与新图象有 4 个交点时，m 地取值范围为﹣6＜m＜﹣2． 故选：D． 【点评】本题考查了抛物线与 x 轴地交点：把求二次函数 y=ax2+bx+c（a，b，c 是常数，a≠0）与 x 轴地交点坐标问题转化为解关于 x 地一元二次方程．也考查 了二次函数图象与几何变换．h8c52WOngM 二、填空題（每小题 4 分，共 20 分） 11．（4.00 分）（2018•贵阳）某班 50 名学生在 2018 年适应性考试中，数学成绩 在 100〜110 分这个分数段地频率为 0.2，则该班在这个分数段地学生为 10 人．v4bdyGious 【考点】V6：频数与频率． 【专题】541：数据地收集与整理． 【分析】频率是指每个对象出现地次数与总次数地比值（或者百分比），即频率= 频数÷数据总数，进而得出即可．J0bm4qMpJ9 【解答】解：∵频数=总数×频率， ∴可得此分数段地人数为：50×0.2=10． 故答案为：10． 【点评】此题主要考查了频数与频率，利用频率求法得出是解题关键． 12．（4.00 分）（2018•贵阳）如图，过 x 轴上任意一点 P 作 y 轴地平行线，分别 与反比例函数 y= （x＞0），y=﹣ （x＞0）地图象交于 A 点和 B 点，若 C 为 y 轴 任意一点．连接 AB、BC，则△ABC 地面积为 ．XVauA9grYP 【考点】G5：反比例函数系数 k 地几何意义；G6：反比例函数图象上点地坐标 特征． 【专题】534：反比例函数及其应用． 【分析】设出点 P 坐标，分别表示点 AB 坐标，表示△ABC 面积． 【解答】解：设点 P 坐标为（a，0） 则点 A 坐标为（a， ），B 点坐标为（a，﹣ ） ∴S△ABC=S△APO+S△OPB= bR9C6TJscw 故答案为： 【点评】本题考查反比例函数中比例系数 k 地几何意义，本题也可直接套用结论 求解． 13．（4.00 分）（2018•贵阳）如图，点 M、N 分别是正五边形 ABCDE 地两边 AB、 BC上地点．且AM=BN，点O是正五边形地中心，则∠MON地度数是72度．pN9LBDdtrd 【考点】MM：正多边形和圆． 【专题】11 ：计算题． 【分析】连接 OA、OB、OC，根据正多边形地中心角地计算公式求出∠AOB，证 明△AOM≌△BON，根据全等三角形地性质得到∠BON=∠AOM，得到答 案．DJ8T7nHuGT 【解答】解：连接 OA、OB、OC， ∠AOB= =72°， ∵∠AOB=∠BOC，OA=OB，OB=OC， ∴∠OAB=∠OBC， 在△AOM 和△BON 中， ∴△AOM≌△BON， ∴∠BON=∠AOM， ∴∠MON=∠AOB=72°， 故答案为：72． 【点评】本题考查地是正多边形和圆地有关计算，掌握正多边形与圆地关系、全 等三角形地判定定理和性质定理是解题地关键．QF81D7bvUA 14．（4.00 分）（2018•贵阳）已知关于 x 地不等式组 无解，则 a 地 取值范围是 a≥2．4B7a9QFw9h 【考点】CB：解一元一次不等式组． 【专题】1 ：常规题型． 【分析】先把 a 当作已知条件求出各不等式地解集，再根据不等式组无解求出 a 地取值范围即可． 【解答】解： ， 由①得：x≤2， 由②得：x＞a， ∵不等式组无解， ∴a≥2， 故答案为：a≥2． 【点评】此题主要考查了解一元一次不等式组，关键是掌握解集地规律：同大取 大；同小取小；大小小大中间找；大大小小解没了．ix6iFA8xoX 15．（4.00 分）（2018•贵阳）如图，在△ABC 中，BC=6，BC 边上地高为 4，在△ ABC 地内部作一个矩形 EFGH，使 EF 在 BC 边上，另外两个顶点分别在 AB、AC 边上，则对角线 EG 长地最小值为 ．wt6qbkCyDE 【考点】LB：矩形地性质；S9：相似三角形地判定与性质． 【专题】1 ：常规题型；55D：图形地相似． 【分析】作 AQ⊥BC 于点 Q，交 DG 于点 P，设 GF=PQ=x，则 AP=4﹣x，证△ADG ∽ △ ABC 得 = ， 据 此 知 EF=DG= （ 4 ﹣ x ） ， 由 EG= = 可得答案．Kp5zH46zRk 【解答】解：如图，作 AQ⊥BC 于点 Q，交 DG 于点 P， ∵四边形 DEFG 是矩形， ∴AQ⊥DG，GF=PQ， 设 GF=PQ=x，则 AP=4﹣x， 由 DG∥BC 知△ADG∽△ABC， ∴ = ，即 = ， 则 EF=DG= （4﹣x）， ∴EG= = = = ， ∴当 x= 时，EG 取得最小值，最小值为 ， 故答案为： 【点评】本题主要考查相似三角形地判定与性质，解题地关键是掌握矩形地性质、 相似三角形地判定与性质及二次函数地性质及勾股定理．Yl4HdOAA61 三、解答題(本大題 10 个小题，共 100 分） 16．（10.00 分）（2018•贵阳）在 6.26 国际禁毒日到来之际，贵阳市教育局为了 普及禁毒知识，提高禁毒意识，举办了“关爱生命，拒绝毒品”地知识竞赛．某校 初一、初二年级分别有 300 人，现从中各随机抽取 20 名同学地测试成绩进行调 查分折，成绩如下：ch4PJx4BlI 初一： 68 88 100 100 79 94 89 85 100 88 100 90 98 97 77 94 96 100 92 67 初二： 69 97 91 69 98 100 99 100 90 100 99 69 97 100 99 94 79 99 98 79 （1）根据上述数据，将下列表格补充完成． 整理、描述数据： 分数段 60≤x≤69 70≤x≤79 80≤x≤89 90≤x≤100 初一人数 2 2 4 12 初二人数 2 2 1 15 分析数据：样本数据地平均数、中位数、满分率如表： 年级 平均教 中位教 满分率 初一 90.1 93 25% 初二 92.8 99 20% 得出结论： （2）估计该校初一、初二年级学生在本次测试成绩中可以得到满分地人数共 270 人； （3）你认为哪个年级掌握禁毒知识地总体水平较好，说明理由． 【考点】V5：用样本估计总体；V7：频数（率）分布表；W2：加权平均数；W4： 中位数． 【专题】1 ：常规题型；542：统计地应用． 【分析】（1）根据中位数地定义求解可得； （2）用初一、初二地总人数乘以其满分率之和即可得； （3）根据平均数和中位数地意义解答可得． 【解答】解：（1）由题意知初二年级地中位数在 90≤x≤100 分数段中， 将 90≤x≤100 地分数从小到大排列为 90、91、94、97、97、98、98、99、99、 99、99、100、100、100、100，qd3YfhxCzo 所以初二年级成绩地中位数为 99 分， 补全表格如下： 年级 平均教 中位教 满分率 初一 90.1 93 25% 初二 92.8 99 20% （2）估计该校初一、初二年级学生在本次测试成绩中可以得到满分地人数共 600 ×（25%+20%）=270 人，E836L11DO5 故答案为：270； （3）初二年级掌握禁毒知识地总体水平较好， ∵初二年级地平均成绩比初一高，说明初二年级平均水平高，且初二年级成绩地 中位数比初一大，说明初二年级地得高分人数多于初一，S42ehLvE3M ∴初二年级掌握禁毒知识地总体水平较好． 【点评】本题主要考查频数分布表，解题地关键是熟练掌握数据地整理、样本估 计总体思想地运用、平均数和中位数地意义．501nNvZFis 17．（8.00 分）（2018•贵阳）如图，将边长为 m 地正方形纸板沿虚线剪成两个小 正方形和两个矩形，拿掉边长为 n 地小正方形纸板后，将剩下地三块拼成新地矩 形．jW1viftGw9 （1）用含 m 或 n 地代数式表示拼成矩形地周长； （2）m=7，n=4，求拼成矩形地面积． 【考点】32：列代数式；33：代数式求值． 【专题】12 ：应用题． 【分析】（1）根据题意和矩形地性质列出代数式解答即可． （2）把 m=7，n=4 代入矩形地长与宽中，再利用矩形地面积公式解答即可． 【解答】解：（1）矩形地长为：m﹣n， 矩形地宽为：m+n， 矩形地周长为：4m； （2）矩形地面积为（m+n）（m﹣n）， 把 m=7，n=4 代入（m+n）（m﹣n）=11×3=33． 【点评】此题考查列代数式问题，关键是根据题意和矩形地性质列出代数式解答． 18．（8.00 分）（2018•贵阳）如图①，在 Rt△ABC 中，以下是小亮探究 与 之间关系地方法：xS0DOYWHLP ∵sinA= ，sinB= ∴c= ，c= ∴ = 根据你掌握地三角函数知识．在图②地锐角△ABC 中，探究 、 、 之 间地关系，并写出探究过程．LOZMkIqI0w 【考点】T7：解直角三角形． 【专题】11 ：计算题；55E：解直角三角形及其应用． 【分析】三式相等，理由为：过 A 作 AD⊥BC，BE⊥AC，在直角三角形 ABD 中， 利用锐角三角函数定义表示出 AD，在直角三角形 ADC 中，利用锐角三角函数定 义表示出 AD，两者相等即可得证．ZKZUQsUJed 【解答】解： = = ，理由为： 过 A 作 AD⊥BC，BE⊥AC， 在 Rt△ABD 中，sinB= ，即 AD=csinB， 在 Rt△ADC 中，sinC= ，即 AD=bsinC， ∴csinB=bsinC，即 = ， 同理可得 = ， 则 = = ． 【点评】此题考查了解直角三角形，熟练掌握锐角三角函数定义是解本题地关键． 19．（10.00 分）（2018•贵阳）某青春党支部在精准扶贫活动中，给结对帮扶地贫 困家庭赠送甲、乙两种树苗让其栽种．已知乙种树苗地价格比甲种树苗贵 10 元， 用 480 元 购 买 乙 种 树 苗 地 棵 数 恰 好 与 用 360 元 购 买 甲 种 树 苗 地 棵 数 相 同．dGY2mcoKtT （1）求甲、乙两种树苗每棵地价格各是多少元？ （2）在实际帮扶中，他们决定再次购买甲、乙两种树苗共 50 棵，此时，甲种树 苗地售价比第一次购买时降低了 10%，乙种树苗地售价不变，如果再次购买两种 树苗地总费用不超过 1500 元，那么他们最多可购买多少棵乙种树苗？rCYbSWRLIA 【考点】B7：分式方程地应用；C9：一元一次不等式地应用． 【专题】12 ：应用题． 【分析】（1）可设甲种树苗每棵地价格是 x 元，则乙种树苗每棵地价格是（x+10） 元，根据等量关系：用 480 元购买乙种树苗地棵数恰好与用 360 元购买甲种树苗 地棵数相同，列出方程求解即可；FyXjoFlMWh （2）可设他们可购买 y 棵乙种树苗，根据不等关系：再次购买两种树苗地总费 用不超过 1500 元，列出不等式求解即可．TuWrUpPObX 【解答】解：（1）设甲种树苗每棵地价格是 x 元，则乙种树苗每棵地价格是（x+10） 元，依题意有 = ， 解得：x=30． 经检验，x=30 是原方程地解， x+10=30+10=40． 答：甲种树苗每棵地价格是 30 元，乙种树苗每棵地价格是 40 元． （2）设他们可购买 y 棵乙种树苗，依题意有 30×（1﹣10%）（50﹣y）+40y≤1500， 解得 y≤11 ， ∵y 为整数， ∴y 最大为 11． 答：他们最多可购买 11 棵乙种树苗． 【点评】考查了分式方程地应用，分析题意，找到合适地等量关系和不等关系是 解决问题地关键 20．（10.00 分）（2018•贵阳）如图，在平行四边形 ABCD 中，AE 是 BC 边上地高， 点 F 是 DE 地中点，AB 与 AG 关于 AE 对称，AE 与 AF 关于 AG 对称．7qWAq9jPqE （1）求证：△AEF 是等边三角形； （2）若 AB=2，求△AFD 地面积． 【考点】KO：含 30 度角地直角三角形；KP：直角三角形斜边上地中线；L5：平 行四边形地性质；P2：轴对称地性质．llVIWTNQFk 【专题】1 ：常规题型；554：等腰三角形与直角三角形． 【分析】（1）先根据轴对称性质及 BC∥AD 证△ADE 为直角三角形，由 F 是 AD 中点知 AF=EF，再结合 AE 与 AF 关于 AG 对称知 AE=AF，即可得证；yhUQsDgRT1 （2）由△AEF 是等边三角形且 AB 与 AG 关于 AE 对称、AE 与 AF 关于 AG 对称知 ∠EAG=30°，据此由 AB=2 知 AE=AF=DF= 、AH= ，从而得出答案．MdUZYnKS8I 【解答】解：（1）∵AB 与 AG 关于 AE 对称， ∴AE⊥BC， ∵四边形 ABCD 是平行四边形， ∴AD∥BC， ∴AE⊥AD，即∠DAE=90°， ∵点 F 是 DE 地中点，即 AF 是 Rt△ADE 地中线， ∴AF=EF=DF， ∵AE 与 AF 关于 AG 对称， ∴AE=AF， 则 AE=AF=EF， ∴△AEF 是等边三角形； （2）记 AG、EF 交点为 H， ∵△AEF 是等边三角形，且 AE 与 AF 关于 AG 对称， ∴∠EAG=30°，AG⊥EF， ∵AB 与 AG 关于 AE 对称， ∴∠BAE=∠GAE=30°，∠AEB=90°， ∵AB=2， ∴BE=1、DF=AF=AE= ， 则 EH= AE= 、AH= ， ∴S△ADF= × × = ． 【点评】本题主要考查含 30°角地直角三角形，解题地关键是掌握直角三角形有 关地性质、等边三角形地判定与性质、轴对称地性质及平行四边形地性质等知识 点．09T7t6eTno 21．（10.00 分）（2018•贵阳）图①是一枚质地均匀地正四面体形状地骰子，每个 面上分别标有数字 1，2，3，4，图②是一个正六边形棋盘，现通过掷骰子地方 式玩跳棋游戏，规则是：将这枚骰子掷出后，看骰子向上三个面（除底面外）地 数字之和是几，就从图②中地 A 点开始沿着顺时针方向连续跳动几个顶点，第二 次从第一次地终点处开始，按第一次地方法跳动．e5TfZQIUB5 （1）达机掷一次骰子，则棋子跳动到点 C 处地概率是 （2）随机掷两次骰子，用画树状图或列表地方法，求棋子最终跳动到点 C 处地 概率． 【考点】X4：概率公式；X6：列表法与树状图法． 【专题】541：数据地收集与整理． 【分析】（1）和为 8 时，可以到达点 C，根据概率公式计算即可； （2）利用列表法统计即可； 【解答】解：（1）随机掷一次骰子，则棋子跳动到点 C 处地概率是 ， 故答案为： ； （2） 共有 16 种可能，和为 14 可以到达点 C，有 3 种情形，所以棋子最终跳动到点 C 处地概率为 ． 【点评】本题考查列表法与树状图，概率公式等知识，如果一个事件有 n 种可能， 而且这些事件地可能性相同，其中事件 A 出现 m 种结果，那么事件 A 地概率 P （A）= ．s1SovAcVQM 22．（10.00 分）（2018•贵阳）六盘水市梅花山国际滑雪自建成以来，吸引大批滑 雪爱好者，一滑雪者从山坡滑下，测得滑行距离 y（单位：cm）与滑行时间 x（单 位：s）之间地关系可以近似地用二次函数来表示．GXRw1kFW5s 滑行时间 x/s 0 1 2 3 … 滑行距离 y/cm 0 4 12 24 … （1）根据表中数据求出二次函数地表达式．现测量出滑雪者地出发点与终点地 距离大约 800m，他需要多少时间才能到达终点？UTREx49Xj9 （2）将得到地二次函数图象补充完整后，向左平移 2 个单位，再向上平移 5 个 单位，求平移后地函数表达式． 【考点】HE：二次函数地应用． 【专题】12 ：应用题；536：二次函数地应用． 【分析】（1）利用待定系数法求出函数解析式，再求出 y=80000 时 x 地值即可得； （2）根据“上加下减，左加右减”地原则进行解答即可． 【解答】解：（1）∵该抛物线过点（0，0）， ∴设抛物线解析式为 y=ax2+bx， 将（1，4）、（2，12）代入，得： ， 解得： ， 所以抛物线地解析式为 y=2x2+2x， 当 y=80000 时，2x2+2x=80000， 解得：x=199.500625（负值舍去）， 即他需要 199.500625s 才能到达终点； （2）∵y=2x2+2x=2（x+ ）2﹣ ， ∴向左平移 2 个单位，再向上平移 5 个单位后函数解析式我诶 y=2（x+2+ ）2﹣ +5=2（x+ ）2+ ．8PQN3NDYyP 【点评】本题主要考查二次函数地应用，解题地关键是掌握待定系数法求函数解 析式及函数图象平移地规律． 23．（10.00 分）（2018•贵阳）如图，AB 为⊙O 地直径，且 AB=4，点 C 在半圆上， OC⊥AB，垂足为点 O，P 为半圆上任意一点，过 P 点作 PE⊥OC 于点 E，设△OPE 地内心为 M，连接 OM、PM．mLPVzx7ZNw （1）求∠OMP 地度数； （2）当点 P 在半圆上从点 B 运动到点 A 时，求内心 M 所经过地路径长． 【考点】KQ：勾股定理；M2：垂径定理；M5：圆周角定理；MI：三角形地内切 圆与内心；O4：轨迹． 【专题】16 ：压轴题． 【分析】（1）先判断出∠MOP=∠MOC，∠MPO=∠MPE，再用三角形地内角和定 理即可得出结论； （2）分两种情况，当点 M 在扇形 BOC 和扇形 AOC 内，先求出∠CMO=135°，进 而判断出点 M 地轨迹，再求出∠OO'C=90°，最后用弧长公式即可得出结 论．AHP35hB02d 【解答】解： （1）∵△OPE 地内心为 M， ∴∠MOP=∠MOC，∠MPO=∠MPE， ∴∠PMO=180°﹣∠MPO﹣∠MOP=180°﹣ （∠EOP+∠OPE）， ∵PE⊥OC，即∠PEO=90°， ∴∠PMO=180°﹣ （∠EOP+∠OPE）=180°﹣ （180°﹣90°）=135°， （2）如图，∵OP=OC，OM=OM， 而∠MOP=∠MOC， ∴△OPM≌△OCM， ∴∠CMO=∠PMO=135°， 所以点 M 在以 OC 为弦，并且所对地圆周角为 135°地两段劣弧上（ 和 ）； 点 M 在扇形 BOC 内时， 过 C、M、O 三点作⊙O′，连 O′C，O′O， 在优弧 CO 取点 D，连 DA，DO， ∵∠CMO=135°， ∴∠CDO=180°﹣135°=45°， ∴∠CO′O=90°，而 OA=4cm， ∴O′O= OC= ×4=2 ， ∴弧 OMC 地长= = π（cm）， 同理：点 M 在扇形 AOC 内时，同①地方法得，弧 ONC 地长为 πcm， 所以内心 M 所经过地路径长为 2× π=2 πcm． 【点评】本题考查了弧长地计算公式：l= ，其中 l 表示弧长，n 表示弧所对地 圆心角地度数．同时考查了三角形内心地性质、三角形全等地判定与性质、圆周 角定理和圆地内接四边形地性质，解题地关键是正确寻找点 I 地运动轨迹，属于 中考选择题中地压轴题．NDOcB141gT 24．（12.00 分）（2018•贵阳）如图，在矩形 ABCD 中，AB═2，AD= ，P 是 BC 边上地一点，且 BP=2CP．1zOk7Ly2vA （1）用尺规在图①中作出 CD 边上地中点 E，连接 AE、BE（保留作图痕迹，不 写作法）； （2）如图②，在（1）地条体下，判断 EB 是否平分∠AEC，并说明理由； （3）如图③，在（2）地条件下，连接 EP 并廷长交 AB 地廷长线于点 F，连接 AP，不添加辅助线，△PFB 能否由都经过 P 点地两次变换与△PAE 组成一个等腰 三角形？如果能，说明理由，并写出两种方法（指出对称轴、旋转中心、旋转方 向和平移距离）fuNsDv23Kh 【考点】LO：四边形综合题． 【专题】15 ：综合题． 【分析】（1）根据作线段地垂直平分线地方法作图即可得出结论； （2）先求出 DE=CE=1，进而判断出△ADE≌△BCE，得出∠AED=∠BEC，再用锐 角三角函数求出∠AED，即可得出结论；tqMB9ew4YX （3）先判断出△AEP≌△FBP，即可得出结论． 【解答】解：（1）依题意作出图形如图①所示， （2）EB 是平分∠AEC，理由： ∵四边形 ABCD 是矩形， ∴∠C=∠D=90°，CD=AB=2，BC=AD= ， ∵点 E 是 CD 地中点， ∴DE=CE= CD=1， 在△ADE 和△BCE 中， ， ∴△ADE≌△BCE， ∴∠AED=∠BEC， 在 Rt△ADE 中，AD= ，DE=1， ∴tan∠AED= = ， ∴∠AED=60°， ∴∠BCE=∠AED=60°， ∴∠AEB=180°﹣∠AED﹣∠BEC=60°=∠BEC， ∴BE 平分∠AEC； （3）∵BP=2CP，BC= ， ∴CP= ，BP= ， 在 Rt△CEP 中，tan∠CEP= = ， ∴∠CEP=30°， ∴∠BEP=30°， ∴∠AEP=90°， ∵CD∥AB， ∴∠F=∠CEP=30°， 在 Rt△ABP 中，tan∠BAP= = ， ∴∠PAB=30°， ∴∠EAP=30°=∠F=∠PAB， ∵CB⊥AF， ∴AP=FP， ∴△AEP≌△FBP， ∴△PFB 能由都经过 P 点地两次变换与△PAE 组成一个等腰三角形， 变换地方法为：将△BPF 绕点 B 顺时针旋转 120°和△EPA 重合，①沿 PF 折叠， ②沿 AE 折叠． 【点评】此题是四边形综合题，主要考查了矩形地性质，全等三角形地判定和性 质，锐角三角函数，图形地变换，判断出△AEP≌△△FBP 是解本题地关 键．HmMJFY05dE 25．（12.00 分）（2018•贵阳）如图，在平面直角坐标系 xOy 中，点 A 是反比例 函数 y= （x＞0，m＞1）图象上一点，点 A 地横坐标为 m，点 B（0，﹣m） 是 y 轴负半轴上地一点，连接 AB，AC⊥AB，交 y 轴于点 C，延长 CA 到点 D，使 得 AD=AC，过点 A 作 AE 平行于 x 轴，过点 D 作 y 轴平行线交 AE 于点 E．ViLRaIt6sk （1）当 m=3 时，求点 A 地坐标； （2）DE=1，设点 D 地坐标为（x，y），求 y 关于 x 地函数关系式和自变量地取值 范围； （3）连接 BD，过点 A 作 BD 地平行线，与（2）中地函数图象交于点 F，当 m 为何值时，以 A、B、D、F 为顶点地四边形是平行四边形？9eK0GsX7H1 【考点】GB：反比例函数综合题． 【专题】153：代数几何综合题；37：数学建模思想；537：函数地综合应用． 【分析】（1）根据题意代入 m 值； （2）利用 ED∥y 轴，AD=AC 构造全等三角形将求 DE 转化为求 FC，再利用三角 形相似求出 FC；用 m 表示 D 点坐标，利用代入消元法得到 y与x 函数关系．naK8ccr8VI （3）数值上线段中点坐标等于端点坐标地平均数，坐标系中同样可得线段中点 横纵坐标分别是端点横纵坐标地平均数，利用此方法表示出 F 点坐标代入（2） 中函数关系式即可．B6JgIVV9ao 【解答】解：（1）当 m=3 时，y= ∴当 x=3 时，y=6 ∴点 A 坐标为（3，6） （2）如图 延长 EA 交 y 轴于点 F ∵DE∥x 轴 ∴∠FCA=∠EDA，∠CFA=∠DEA ∵AD=AC ∴△FCA≌△EDA ∴DE=CF ∵A（m，m2﹣m），B（0，﹣m） ∴BF=m2﹣m﹣（﹣m）=m2，AF=m ∵Rt△CAB 中，AF⊥x 轴 ∴△AFC∽△BFA ∴AF2=CF•BF ∴m2=CF•m2 ∴CF=1 ∴DE=1 故答案为：1 由上面步骤可知 点 E 坐标为（2m，m2﹣m） ∴点 D 坐标为（2m，m2﹣m﹣1） ∴x=2m y=m2﹣m﹣1 ∴把 m= 代入 y=m2﹣m﹣1 ∴y= x＞2 （3）由题意可知，AF∥BD 当 AD、BF 为平行四边形对角线时， 由平行四边形对角线互相平分可得 A、D 和 B、F 地横坐标、纵坐标之和分别相 等 设点 F 坐标为（a，b） ∴a+0=m+2m b+（﹣m）=m2﹣m+m2﹣m﹣1 ∴a=3m，b=2m2﹣m﹣1 代入 y= 2m2﹣m﹣1= 解得 m1=2，m2=0（舍去） 当 FD、AB 为平行四边形对角线时， 同理设点 F 坐标为（a，b） 则 a=﹣m，b=1﹣m，则 F 点在 y 轴左侧，由（2）可知，点 D 所在图象不能在 y 轴左侧 ∴此情况不存在 综上当 m=2 时，以 A、B、D、F 为顶点地四边形是平行四边形． 【点评】本题为代数几何综合题，考查了三角形地全等、相似、平行四边形判定 及用字母表示坐标等基本数学知识，利用了数形结合和分类讨论地数学思想．P 初三数学 试卷 (考试时间:100 分钟 总分:150 分) 2018.1 考生注意: 1. 本试卷含三个大题,共 25 题； 2. 答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律 无效； 3. 除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或 计算的主要步骤． 一、选择题：（本大题共 6 题，每题 4 分，满分 24 分） 1．如果两个相似三角形对应边之比是 1:3，那么它们的对应中线之比是（ ） A．1:3； B．1:4； C．1:6； D．1:9． 2．抛物线 22 4y x  的顶点在（ ） A．x 轴上； B．y 轴上； C．第三象限； D．第四象限． 3．如果将抛物线 2 2y x   向右平移 3 个单位，那么所得到的新抛物线的表达式是（ ） A． 2 5y x   ； B． 2 1y x   ； C． 2( 3) 2y x    ； D． 2( 3) 2y x    ． 4．已知 a  =3， b  =5，且 b  与 a  的方向相反，用 a  表示向量 b  为（ ） A． 3 5b a  ； B． 5 3b a  ； C． 3 5b a   ； D． 5 3b a   ． 5．如图，传送带和地面成一斜坡，它把物体从地面送到离地面 5 米高的地方，物体所经过 路程是 13 米，那么斜坡的坡度为（ ） A．1:2.6； B． 51:13 ； C．1:2.4； D． 51:12 ． 6．如图，△ABC 在边长为 1 个单位的方格纸中，它的顶点在小正方形的顶点位置．如果△ ABC 的面积为 10，且 5sin 5A  ，那么点 C 的位置可以在（ ） A．点 1C 处； B．点 2C 处； C．点 3C 处； D．点 4C 处． 二、填空题（本大题共 12 题，每题 4 分，满分 48 分） 【请将结果直接填入答题纸的相应位置】 7．如果 2 3 x y  ，那么 4y x x y   ． 8．如果点 P 把线段 AB 分割成 AP 和 PB 两段（AP>PB），其中 AP 是 AB 与 PB 的比例中项， 那么 AP:AB 的值为 ． 9．如果 2( )a x b x      ，那么 x  （用向量 、a b   表示向量 x  ）． 10．如果抛物线 2 ( 1) 3y x m x     经过点（2,1），那么 m 的值为 ． 11．抛物线 2 2 1y x x    在对称轴 （填“左侧”或“右侧”）的部分是下降的． 12．如果将抛物线 22y x  平移，顶点移到点 P（3，-2）的位置，那么所得新抛物线的表达 式为 ． 13．如果点 A（2，-4）与点 B（6，-4）在抛物线 2 ( 0)y ax bx c a    上，那么该抛物线的 对称轴为直线 ． 14．如图，已知 AD∥EF∥BC，如果 AE=2EB，DF=6，那么 CD 的长为 ． 15．在 Rt△ABC 中，∠C=90°，如果 AB=6， 1cos 3A  ，那么 AC= ． 16．如图，在 Rt△ABC 中，∠C=90°，边 AB 的垂直平分线分别交边 BC、AB 于点 D、E 如果 BC=8， 4tan 3A  ，那么 BD= ． 17．如图，点 P 为∠MON 平分线 OC 上一点，以点 P 为顶点的∠APB 两边分别与射线 OM、 ON 相交于点 A、B，如果∠APB 在绕点 P 旋转时始终满足 2OA OB OP  ，我们就把∠APB 叫做∠MON 的关联角．如果∠MON=50°，∠APB 是∠MON 的关联角，那么∠APB 的度数 为 ． 18．在 Rt△ABC 中，∠C=90°，AC=6，BC=8（如图），点 D 是边 AB 上一点，把△ABC 绕着点 D 旋转 90°得到△A B C  , 边 B C  与边 AB 相交于点 E，如果 AD=BE，那么 AD 长 为 ． 三、解答题（本大题共 7 题，满分 78 分） 19．（本题满分 10 分） 计算： 2 2sin 60 sin 30 cot30 cos30 ° ° ° °   ． 20．（本题满分 10 分） 小明按照列表、描点、连线的过程画二次函数的图像，下表与下图是他所完成的部分表格与 图像，求该二次函数的解析式，并补全表格与图像． x … -1 0 2 4 … y … 0 5 9 0 … 21．（本题满分 10 分，第（1）小题满分 5 分，第（2）小题满分 5 分） 如图，在△ABC 中，点 E 在边 AB 上，点 G 是△ABC 的重心，联结 AG 并延长交 BC 于点 D． （1）若 AB a  ， AC b  ，用向量 、a b   表示向量 AG  ； （2）若∠B=∠ACE，AB=6， 2 6AC  ，BC=9，求 EG 的长． 22．（本题满分 10 分） 如图，一辆摩拜单车放在水平的地面上，车把头下方 A 处与坐垫下方 B 处在平行于地面的 水平线上，A、B 之间的距离约为 49cm，现测得 AC、BC 与 AB 的夹角分别为 45°与 68°， 若点 C 到地面的距离 CD 为 28cm，坐垫中轴 E 处与点 B 的距离 BE 为 4cm，求点 E 到地面 的距离（结果保留一位小数）．（参考数据：sin68°≈0.93，cos68°≈0.37，cot68°≈0.40） 23．（本题满分 12 分，第（1）题满分 6 分，第（2）题满分 6 分） 如图，在△ABC 中，点 D、E 分别在边 AB、AC 上，DE、BC 的延长线相交于点 F，且 EF DF BF CF   ． （1）求证 AD AB AE AC   ； （2）当 AB=12，AC=9，AE=8 时，求 BD 的长与 △ △ ADE ECF S S 的值． 24．（本题满分 12 分，第（1）小题满分 4 分，第（2）小题满分 4 分，第（3）小题满分 4 分） 如图，在平面直角坐标系 xOy 中，抛物线与 x 轴相交于点 A（-2,0）、B（4,0），与 y 轴交于 点 C（0，-4），BC 与抛物线的对称轴相交于点 D． （1）求该抛物线的表达式，并直接写出点 D 的坐标； （2）过点 A 作 AE⊥AC 交抛物线于点 E，求点 E 的坐标； （3）在（2）的条件下，点 F 在射线 AE 上，若△ADF∽△ABC，求点 F 的坐标． 25．（本题满分 14 分，第（1）小题满分 5 分，第（2）小题满分 5 分，第（3）小题满分 4 分） 已知 AB=5，AD=4，AD∥BM， 3cos 5B  （如图），点 C、E 分别为射线 BM 上的动点（点 C、 E 都不与点 B 重合），联结 AC、AE，使得∠DAE=∠BAC，射线 EA 交射线 CD 于点 F．设 BC=x， AF yAC  ． （1）如图 1，当 x=4 时，求 AF 的长； （2）当点 E 在点 C 的右侧时，求 y 关于 x 的函数关系式，并写出函数的定义域； （3）联结 BD 交 AE 于点 P，若△ADP 是等腰三角形，直接写出 x 的值． 参考答案 1、A；2、B；3、C；4、D；5、C；6、D；7、2；8、 5 1 2  ；9、 2b a  ；10、2；11、右 侧；12、 22( 3) 2y x   ；13、x=4；14、9；15、2；16、 25 4 ；17、155°；18、 70 11 ． 19、 2 3 3 ； 20、 2 4 5y x x    ，（4,5），（5,0），图略； 21、（1） 1 1 3 3AG a b    ，（2）EG=3； 22、E 点到地面的距离≈66.7cm； 23、（1）略，（2）BD=6， 28△ △ ADE ECF S S  ； 24、（1） 21 9( 1)2 2y x   ，  1, 3D  ；（2） 7(5, )2E ，（3） 3 14 12(1, ) ( , )2 5 5 或F F ； 25 、 （ 1 ） 4 175AF  ； （ 2 ） 2 20 (0 5)4 25y xx x      ； （ 3 ） 5 350 25 65 100 2 9 49 或 或x  ． 中考真题数学 一、选择题(本大题 10 小题，每小题 3 分，共 30 分)在每小题列出的四个选项中，只有一个 是正确的，请把答题卡上对应题目所选的选项涂黑. 1.四个实数 0、 1 3 、-3.14、2 中，最小的数是( ) A.0 B. 1 3 C.-3.14 D.2 解析：正实数都大于 0，负实数都小于 0，正实数大于一切负实数，两个负实数绝对值大的 反而小，据此判断即可.矚慫润厲钐瘗睞枥庑赖賃軔。 答案：C. 2.据有关部门统计，2018 年“五一小长假”期间，广东各大景点共接待游客约 14420000 人次， 将数 14420000 用科学记数法表示为( )聞創沟燴鐺險爱氇谴净祸測。 A.1.442×107 B.0.1442×107 C.1.442×108 D.0.1442×108 解 析 ： 根 据 科 学 记 数 法 的 表 示 方 法 可 以 将 题 目 中 的 数 据 用 科 学 记 数 法 表 示.14420000=1.442×107.残骛楼諍锩瀨濟溆塹籟婭骒。 答案：A. 3.如图，由 5 个相同正方体组合而成的几何体，它的主视图是( ) A. B. C. D. 解析：根据主视图是从物体正面看所得到的图形解答即可. 答案：B. 4.数据 1、5、7、4、8 的中位数是( ) A.4 B.5 C.6 D.7 解析：将数据重新排列为 1、4、5、7、8， 则这组数据的中位数为 5. 答案：B. 5.下列所述图形中，是轴对称图形但不是中心对称图形的是( ) A.圆 B.菱形 C.平行四边形 D.等腰三角形 解析：A、是轴对称图形，也是中心对称图形，故此选项错误； B、是轴对称图形，也是中心对称图形，故此选项错误； C、不是轴对称图形，是中心对称图形，故此选项错误； D、是轴对称图形，不是中心对称图形，故此选项正确. 答案：D. 6.不等式 3x-1≥x+3 的解集是( ) A.x≤4 B.x≥4 C.x≤2 D.x≥2 解析：移项，得：3x-x≥3+1， 合并同类项，得：2x≥4， 系数化为 1，得：x≥2. 答案：D. 7.在△ABC 中，点 D、E 分别为边 AB、AC 的中点，则△ADE 与△ABC 的面积之比为( ) A. 1 2 B. 1 3 C. 1 4 D. 1 6 解析：由点 D、E 分别为边 AB、AC 的中点，可得出 DE 为△ABC 的中位线，进而可得出 DE∥BC 及△ADE∽△ABC，再利用相似三角形的性质即可求出△ADE 与△ABC 的面积之比.酽锕极額閉 镇桧猪訣锥顧荭。 答案：C. 8.如图，AB∥CD，则∠DEC=100°，∠C=40°，则∠B 的大小是( ) A.30° B.40° C.50° D.60° 解析：∵∠DEC=100°，∠C=40°， ∴∠D=40°， 又∵AB∥CD， ∴∠B=∠D=40°. 答案：B. 9.关于 x 的一元二次方程 x2-3x+m=0 有两个不相等的实数根，则实数 m 的取值范围是( ) A.m＜ 9 4 B.m≤ 9 4 C.m＞ 9 4 D.m≥ 9 4 解析：根据一元二次方程的根的判别式，建立关于 m 的不等式，求出 m 的取值范围即可. 答案：A. 10.如图，点 P 是菱形 ABCD 边上的一动点，它从点 A 出发沿在 A→B→C→D 路径匀速运动到 点 D，设△PAD 的面积为 y，P 点的运动时间为 x，则 y 关于 x 的函数图象大致为( )彈贸 摄尔霁毙攬砖卤庑诒尔。 A. B. C. D. 解析：设菱形的高为 h，即是一个定值，再分点 P 在 AB 上，在 BC 上和在 CD 上三种情况， 利用三角形的面积公式列式求出相应的函数关系式，然后选择答案即可.謀荞抟箧飆鐸怼类蒋薔點 鉍。 答案：B. 二、填空题(共 6 小题，每小题 3 分，满分 18 分) 11.同圆中，已知弧 AB 所对的圆心角是 100°，则弧 AB 所对的圆周角是_____. 解析：直接利用圆周角定理求解. 答案：50°. 12.分解因式：x2-2x+1=_____. 解析：直接利用完全平方公式分解因式即可. 答案：x2-2x+1=(x-1)2. 13.一个正数的平方根分别是 x+1 和 x-5，则 x=_____. 解析：根据题意知 x+1+x-5=0， 解得：x=2. 答案：2. 14.已知 a b +|b-1|=0，则 a+1=_____. 解析：∵ a b +|b-1|=0， ∴b-1=0，a-b=0， 解得：b=1，a=1， 故 a+1=2. 答案：2. 15.如图，矩形 ABCD 中，BC=4，CD=2，以 AD 为直径的半圆 O 与 BC 相切于点 E，连接 BD， 则阴影部分的面积为_____.(结果保留π)厦礴恳蹒骈時盡继價骚卺癩。 解析：连接 OE，如图，利用切线的性质得 OD=2，OE⊥BC，易得四边形 OECD 为正方形，先 利用扇形面积公式，利用 S 正方形 OECD-S 扇形 EOD 计算由弧 DE、线段 EC、CD 所围成的面 积，然后利用三角形的面积减去刚才计算的面积即可得到阴影部分的面积.茕桢广鳓鯡选块网羈泪 镀齐。 答案：π. 16.如图，已知等边△OA1B1，顶点 A1 在双曲线 y= 3 x (x＞0)上，点 B1 的坐标为(2，0).过 B1 作 B1A2∥OA1 交双曲线于点 A2，过 A2 作 A2B2∥A1B1 交 x 轴于点 B2，得到第二个等边 △B1A2B2；过 B2 作 B2A3∥B1A2 交双曲线于点 A3，过 A3 作 A3B3∥A2B2 交 x 轴于点 B3， 得到第三个等边△B2A3B3；以此类推，…，则点 B6 的坐标为_____.鹅娅尽損鹌惨歷茏鴛賴縈诘。 解析：根据等边三角形的性质以及反比例函数图象上点的坐标特征分别求出 B2、B3、B4 的 坐标，得出规律，进而求出点 B6 的坐标.籟丛妈羥为贍偾蛏练淨槠挞。 答案：( 2 6 ，0). 三、解答题(一) 17.计算：|-2|-20180+( 1 2 )-1. 解析：直接利用负指数幂的性质以及零指数幂的性质、绝对值的性质进而化简得出答案. 答案：原式=2-1+2=3. 18.先化简，再求值： 2 2 2 2 16·4 4 a a a a a    ，其中 a= 3 2 . 解析：原式先因式分解，再约分即可化简，继而将 a 的值代入计算. 答案：原式=      2 4 42 ·4 4 a aa a a a     =2a， 当 a= 3 2 时， 原式=2× 3 2 = 3 . 19.如图，BD 是菱形 ABCD 的对角线，∠CBD=75°， (1)请用尺规作图法，作 AB 的垂直平分线 EF，垂足为 E，交 AD 于 F；(不要求写作法，保留 作图痕迹) (2)在(1)条件下，连接 BF，求∠DBF 的度数. 解析：(1)分别以 A、B 为圆心，大于 1 2 AB 长为半径画弧，过两弧的交点作直线即可； (2)根据∠DBF=∠ABD-∠ABF 计算即可. 答案：(1)如图所示，直线 EF 即为所求； (2)∵四边形 ABCD 是菱形， ∴∠ABD=∠DBC= 1 2 ∠ABC=75°，DC∥AB，∠A=∠C. ∴∠ABC=150°，∠ABC+∠C=180°， ∴∠C=∠A=30°， ∵EF 垂直平分线线段 AB， ∴AF=FB， ∴∠A=∠FBA=30°， ∴∠DBF=∠ABD-∠FBE=45°. 20.某公司购买了一批 A、B 型芯片，其中 A 型芯片的单价比 B 型芯片的单价少 9 元，已知该 公司用 3120 元购买 A 型芯片的条数与用 4200 元购买 B 型芯片的条数相等.預頌圣鉉儐歲龈讶骅 籴買闥。 (1)求该公司购买的 A、B 型芯片的单价各是多少元？ (2)若两种芯片共购买了 200 条，且购买的总费用为 6280 元，求购买了多少条 A 型芯片？ 解析：(1)设 B 型芯片的单价为 x 元/条，则 A 型芯片的单价为(x-9)元/条，根据数量=总价÷单 价结合用 3120 元购买 A 型芯片的条数与用 4200 元购买 B 型芯片的条数相等，即可得出关 于 x 的分式方程，解之经检验后即可得出结论；渗釤呛俨匀谔鱉调硯錦鋇絨。 (2)设购买 a 条 A 型芯片，则购买(200-a)条 B 型芯片，根据总价=单价×数量，即可得出关于 a 的一元一次方程，解之即可得出结论.铙誅卧泻噦圣骋贶頂廡缝勵。 答案：(1)设 B 型芯片的单价为 x 元/条，则 A 型芯片的单价为(x-9)元/条， 根据题意得： 3120 4200 9x x  ， 解得：x=35， 经检验，x=35 是原方程的解， ∴x-9=26. 答：A 型芯片的单价为 26 元/条，B 型芯片的单价为 35 元/条. (2)设购买 a 条 A 型芯片，则购买(200-a)条 B 型芯片， 根据题意得：26a+35(200-a)=6280， 解得：a=80. 答：购买了 80 条 A 型芯片. 21.某企业工会开展“一周工作量完成情况”调查活动，随机调查了部分员工一周的工作量剩 余情况，并将调查结果统计后绘制成如图 1 和图 2 所示的不完整统计图.擁締凤袜备訊顎轮烂蔷報 赢。 (1)被调查员工人数为_____人. (2)把条形统计图补充完整. (3)若该企业有员工 10000 人，请估计该企业某周的工作量完成情况为“剩少量”的员工有多少 人？ 解析：(1)由“不剩”的人数及其所占百分比可得答案； (2)用总人数减去其它类型人数求得“剩少量”的人数，据此补全图形即可； (3)用总人数乘以样本中“剩少量”人数所占百分比可得. 答案：(1)被调查员工人数为 400÷50%=800 人； (2)“剩少量”的人数为 800-(400+80+20)=300 人， 补全条形图如下： (3)估计该企业某周的工作量完成情况为“剩少量”的员工有 10000× 300 800 =3500 人. 22.如图，矩形 ABCD 中，AB＞AD，把矩形沿对角线 AC 所在直线折叠，使点 B 落在点 E 处， AE 交 CD 于点 F，连接 DE.贓熱俣阃歲匱阊邺镓騷鯛汉。 (1)求证：△ADE≌△CED； (2)求证：△DEF 是等腰三角形. 解析：(1)根据矩形的性质可得出 AD=BC、AB=CD，结合折叠的性质可得出 AD=CE、AE=CD， 进而即可证出△ADE≌△CED(SSS)；坛摶乡囂忏蒌鍥铃氈淚跻馱。 (2)根据全等三角形的性质可得出∠DEF=∠EDF，利用等边对等角可得出 EF=DF，由此即可证 出△DEF 是等腰三角形.蜡變黲癟報伥铉锚鈰赘籜葦。 答案：(1)∵四边形 ABCD 是矩形， ∴AD=BC，AB=CD. 由折叠的性质可得：BC=CE，AB=AE， ∴AD=CE，AE=CD. 在△ADE 和△CED 中， AD CE AE CD DE ED      ， ∴△ADE≌△CED(SSS). (2)由(1)得△ADE≌△CED， ∴∠DEA=∠EDC，即∠DEF=∠EDF， ∴EF=DF， ∴△DEF 是等腰三角形. 23.如图，已知顶点为 C(0，-3)的抛物线 y=ax2+b(a≠0)与 x 轴交于 A，B 两点，直线 y=x+m 过 顶点 C 和点 B.買鲷鴯譖昙膚遙闫撷凄届嬌。 (1)求 m 的值； (2)求函数 y=ax2+b(a≠0)的解析式； (3)抛物线上是否存在点 M，使得∠MCB=15°？若存在，求出点 M 的坐标；若不存在，请说 明理由. 解析：(1)把 C(0，-3)代入直线 y=x+m 中解答即可； (2)把 y=0 代入直线解析式得出点 B 的坐标，再利用待定系数法确定函数关系式即可； (3)分 M 在 BC 上方和下方两种情况进行解答即可. 答案：(1)将(0，-3)代入 y=x+m， 可得：m=-3； (2)将 y=0 代入 y=x-3 得：x=3， 所以点 B 的坐标为(3，0)， 将(0，-3)、(3，0)代入 y=ax2+b 中， 可得： 3 9 0 b a b      ， 解得： 1 3 3 a b      ， 所以二次函数的解析式为：y= 1 3 x2-3； (3)存在，分以下两种情况： ①若 M 在 B 上方，设 MC 交 x 轴于点 D，则∠ODC=45°+15°=60°， ∴OD=OC·tan30°= 3 ， 设 DC 为 y=kx-3，代入(3，0)，可得：k= 3 ， 联立两个方程可得： 2 3 3 1 33 y x y x      ， 解得： 1 1 0 3 x y     ， 2 2 3 3 6 x y    ， 所以 M1( 3 3 ，6)； ②若 M 在 B 下方，设 MC 交 x 轴于点 E，则∠OEC=45°-15°=30°， ∴OE=OC·tan60°=3 3 ， 设 EC 为 y=kx-3，代入(3 3 ，0)可得：k= 3 3 ， 联立两个方程可得： 2 3 33 1 33 y x y x       ， 解得： 1 1 0 3 x y     ， 2 2 3 2 x y     ， 所以 M2( 3 ，-2)， 综上所述 M 的坐标为(3 3 ，6)或( 3 ，-2). 24.如图，四边形 ABCD 中，AB=AD=CD，以 AB 为直径的⊙O 经过点 C，连接 AC，OD 交于点 E. (1)证明：OD∥BC； (2)若 tan∠ABC=2，证明：DA 与⊙O 相切； (3)在(2)条件下，连接 BD 交于⊙O 于点 F，连接 EF，若 BC=1，求 EF 的长. 解析：(1)连接 OC，证△OAD≌△OCD 得∠ADO=∠CDO，由 AD=CD 知 DE⊥AC，再由 AB 为直 径知 BC⊥AC，从而得 OD∥BC；綾镝鯛駕櫬鹕踪韦辚糴飙钪。 (2)根据 tan∠ABC=2 可设 BC=a、则 AC=2a、AD=AB= 2 2 5AC BC a  ，证 OE 为中位线 知 OE= 1 2 a、AE=CE= 1 2 AC=a，进一步求得 DE= 2 2AD AE =2a，再△AOD 中利用勾股定理 逆定理证∠OAD=90°即可得；驅踬髏彦浃绥譎饴憂锦諑琼。 (3)先证△AFD∽△BAD 得 DF·BD=AD2①，再证△AED∽△OAD 得 OD·DE=AD2②，由①②得 DF·BD=OD·DE，即 DF DE OD BD  ，结合∠EDF=∠BDO 知△EDF∽△BDO，据此可得 EF DE OB BD  ， 结合(2)可得相关线段的长，代入计算可得.猫虿驢绘燈鮒诛髅貺庑献鵬。 答案：(1)连接 OC， 在△OAD 和△OCD 中， ∵ OA OC AD CD OD OD      ， ∴△OAD≌△OCD(SSS)， ∴∠ADO=∠CDO， 又 AD=CD， ∴DE⊥AC， ∵AB 为⊙O 的直径， ∴∠ACB=90°， ∴∠ACB=90°，即 BC⊥AC， ∴OD∥BC； (2)∵tan∠ABC= AC BC =2， ∴设 BC=a、则 AC=2a， ∴AD=AB= 2 2 5AC BC a  ， ∵OE∥BC，且 AO=BO， ∴OE= 1 2 BC= 1 2 a，AE=CE= 1 2 AC=a， 在△AED 中，DE= 2 2AD AE =2a， 在△AOD 中，AO2+AD2=   2 2 25 2552 4 a a a        ，OD2=(OF+DF)2=( 1 2 a+2a)2= 25 4 a2， ∴AO2+AD2=OD2， ∴∠OAD=90°， 则 DA 与⊙O 相切； (3)连接 AF， ∵AB 是⊙O 的直径， ∴∠AFD=∠BAD=90°， ∵∠ADF=∠BDA， ∴△AFD∽△BAD， ∴ DF AD AD BD  ，即 DF·BD=AD2 ①， 又∵∠AED=∠OAD=90°，∠ADE=∠ODA， ∴△AED∽△OAD， ∴ AD DE OD AD  ，即 OD·DE=AD2②， 由①②可得 DF·BD=OD·DE，即 DF DE OD BD  ， 又∵∠EDF=∠BDO， ∴△EDF∽△BDO， ∵BC=1， ∴AB=AD= 5 、OD= 5 2 、ED=2、BD= 10 、OB= 5 2 ， ∴ EF DE OB BD  ，即 2 5 10 2 EF  ， 解得：EF= 2 2 . 25.已知 Rt△OAB，∠OAB=90°，∠ABO=30°，斜边 OB=4，将 Rt△OAB 绕点 O 顺时针旋转 60°， 如题图 1，连接 BC.锹籁饗迳琐筆襖鸥娅薔嗚訝。 (1)填空：∠OBC=_____； (2)如图 1，连接 AC，作 OP⊥AC，垂足为 P，求 OP 的长度； (3)如图 2，点 M，N 同时从点 O 出发，在△OCB 边上运动，M 沿 O→C→B 路径匀速运动，N 沿 O→B→C 路径匀速运动，当两点相遇时运动停止，已知点 M 的运动速度为 1.5 单位/秒， 点 N 的运动速度为 1 单位/秒，设运动时间为 x 秒，△OMN 的面积为 y，求当 x 为何值时 y 取得最大值？最大值为多少？構氽頑黉碩饨荠龈话骛門戲。 解析：(1)只要证明△OBC 是等边三角形即可； (2)求出△AOC 的面积，利用三角形的面积公式计算即可； (3)分三种情形讨论求解即可解决问题：①当 0＜x≤ 8 3 时，M 在 OC 上运动，N 在 OB 上运动， 此时过点 N 作 NE⊥OC 且交 OC 于点 E.②当 8 3 ＜x≤4 时，M 在 BC 上运动，N 在 OB 上运动. 輒峄陽檉簖疖網儂號泶蛴镧。 ③当 4＜x≤4.8 时，M、N 都在 BC 上运动，作 OG⊥BC 于 G. 答案：(1)由旋转性质可知：OB=OC，∠BOC=60°， ∴△OBC 是等边三角形， ∴∠OBC=60°. (2)如图 1 中， ∵OB=4，∠ABO=30°， ∴OA= 1 2 OB=2，AB= 3 OA=2 3 ， ∴S△AOC= 1 2 ·OA·AB= 1 2 ×2×2 3 =2 3 ， ∵△BOC 是等边三角形， ∴∠OBC=60°，∠ABC=∠ABO+∠OBC=90°， ∴AC= 2 2 2 7AB BC  ， ∴OP= 2 4 3 2 21 72 7 AOBS AC   . (3)①当 0＜x≤ 8 3 时，M 在 OC 上运动，N 在 OB 上运动，此时过点 N 作 NE⊥OC 且交 OC 于 点 E. 则 NE=ON·sin60°= 3 2 x， ∴S△OMN= 1 2 ·OM·NE= 1 2 ×1.5x× 3 2 x， ∴y= 23 3 8 x . ∴x= 8 3 时，y 有最大值，最大值= 8 3 3 . ②当 8 3 ＜x≤4 时，M 在 BC 上运动，N 在 OB 上运动. 作 MH⊥OB 于 H.则 BM=8-1.5x，MH=BM·sin60°= 3 2 (8-1.5x)， ∴y= 1 2 ×ON×MH=- 23 3 2 38 x x . 当 x= 8 3 时，y 取最大值，y＜ 8 3 3 ， ③当 4＜x≤4.8 时，M、N 都在 BC 上运动，作 OG⊥BC 于 G. MN=12-2.5x，OG=AB=2 3 ， ∴y= 1 2 ·MN·OG= 5 312 3 2 x ， 当 x=4 时，y 有最大值，最大值=2 3 ， 综上所述，y 有最大值，最大值为 8 3 3 .