图形的相似1 8页

‎27.1图形的相似（第1课时）‎ ‎【教学任务分析】‎ 教 学 目 标 知识 技能 ‎1.理解并掌握两个图形相似的概念．‎ ‎2.会判断相似图形.‎ 过程 方法 ‎1.联系生活实际初步认识相似图形，在观察、操作、比较、交流中，探索并发现相似图形的规律；‎ ‎2.经历探索、发现、创造、交流等丰富多彩的数学游戏活动，发展学生的数学能力和审美观.‎ 情感 态度 使学生学会从数学的角度认识世界，解释生活、逐步形成“数学地思维”的习惯；以“生活中的数学”为载体，使学生体会相似图形的神奇，养成“学数学、用数学”的意识，培养学生的动手操作能力和创新精神.‎ 重点 学生自主探索出相似图形的基本特征.‎ 难点 正确地运用相似图形的特征解决生活中实际问题.‎ ‎【教学环节安排】‎ 环节 教 学 问 题 设 计 教学活动设计 问题最佳 解决方案 情 境 引 入 请同学们看黑板正上方的五星红旗，和下图的两个画面，感受它们的形状、大小的关系．（还可以再举几个例子）‎ 教师出示问题 ‎ 从几个图片（如图）引入相似图形，学生自己动手、动脑，亲身体会相似图形与我们的生活有着密切的关系，孕育良好的学习心境，‎ 教师放映图片，并提出问题.‎ 学生通过观察，感性认识形状相同大小不同的含义，并解决教师提出的问题 自 主 探 究 合 问题1. 五星红旗上的大五角星与小五角星他们的形状、大小有什么关系？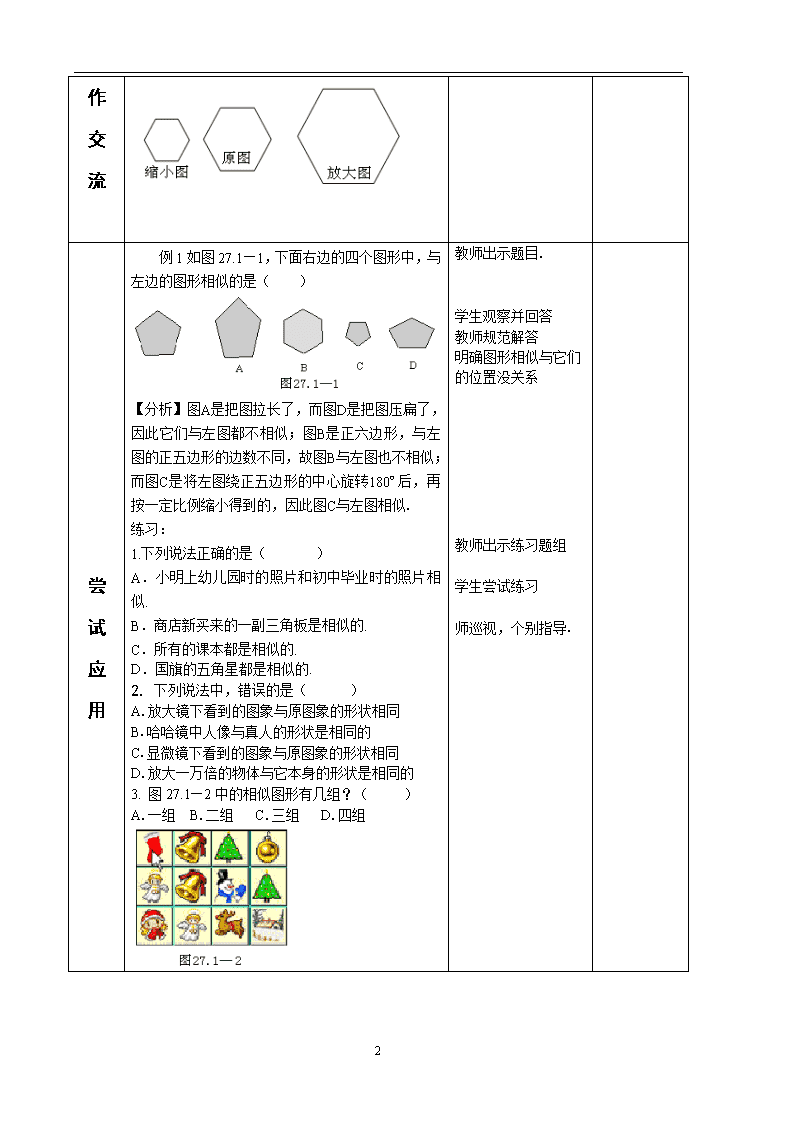‎ 问题2.什么是相似图形?‎ ‎【教师点评】在实际生活中，我们见到过许多大小不一但形状相同的图形，我们把这种形状相同的图形叫做相似图形.‎ 问题3.请同学们举出一些相似的几何图形的例子.‎ 观察课本上的相似图片，‎ 学生通过观察图片，感受形状相同，‎ 大小不同的含义，并得到相似定义．‎ 同学们思考、讨论、交换意见给出实例 教师赞扬举例子比较好的同学.‎ 教师出示以下图片 让学生感受生活中和数学中的相似 8‎ 作 交 流 尝 试 应 用 例1如图27.1—1，下面右边的四个图形中，与左边的图形相似的是（ ）‎ ‎【分析】图A是把图拉长了，而图D是把图压扁了，因此它们与左图都不相似；图B是正六边形，与左图的正五边形的边数不同，故图B与左图也不相似；而图C是将左图绕正五边形的中心旋转180º后，再按一定比例缩小得到的，因此图C与左图相似.‎ 练习：‎ ‎1.下列说法正确的是（ ）‎ A．小明上幼儿园时的照片和初中毕业时的照片相似.‎ B．商店新买来的一副三角板是相似的.‎ C．所有的课本都是相似的.‎ D．国旗的五角星都是相似的.‎ ‎2. 下列说法中，错误的是（　　　）‎ A.放大镜下看到的图象与原图象的形状相同　　‎ B.哈哈镜中人像与真人的形状是相同的 C.显微镜下看到的图象与原图象的形状相同　　‎ D.放大一万倍的物体与它本身的形状是相同的 ‎3. 图27.1—2中的相似图形有几组？（ ）‎ A.一组 B.二组 C.三组 D.四组 教师出示题目.‎ 学生观察并回答 教师规范解答 明确图形相似与它们的位置没关系 教师出示练习题组 学生尝试练习 师巡视，个别指导.‎ 8‎ 成果 展示 ‎1．有条件的可利用多媒体，在几何画板上学生自己操作电脑,同时画出几个相似图形，且具有个性的图画，充分展示学生的个性特点，培养学生的的审美情趣 ‎2．通过本节课的学习，你有哪些收获？‎ 通过所看、所知、所想概括出相似图形的定义、判断相似图形以及相似多边形的性质特征等概念.‎ 师引导学生动手能力训练，培养学生的基本技能.‎ 师引导学生进行展示交流 学生对本节课内容进行归纳总结.‎ 补 偿 提 高 ‎1．如图27.1—3中，相似图形共有几组？　（　　）‎ A.5组　　B.6组　　C.7组　 D.8组 ‎2. 在平面坐标系中，一个图形各点的横坐标、纵坐标都乘以或除以同一个非零数，得到一组新的对应用点，则连接所得到点的图形与原图形形状（　　　）‎ A.能够互相重合 B.形状相同，大小也一定相同　　‎ C.形状不一样　 D.形状相同，大小不一定相同 ‎3. 例尺是1:8000000的“中国政区”地图上，量得福州与上海之间的距离时7.5cm，那么福州与上海之间的实际距离是多少？‎ 教师出示题目.‎ 第1题、第2题由学生独立完成. 教师巡视，个别辅导.‎ 师生共同评析.存在的共性问题共同讨论解决.‎ 第3题鼓励学生独立思考后解决.感觉有困难的学生可以寻求同学的帮助，然后完成.小组交流内.‎ 作 业 设 计 必做题:‎ ‎(1)27.1第1题.‎ ‎(2)AB两地的实际距离为2500m，在一张平面图上的距离是5cm，那么这张平面地图的比例尺是多少？‎ 选做题：‎ P55习题27·2题4，5.‎ 教师布置作业，并提出要求.‎ 学生课下独立完成，延续课堂.‎ 教 后 反 思 ‎【当堂达标自测题】‎ 8‎ 一、填空题 ‎1．观察下列图形，指出 是相似图形.‎ ‎2．形状 的图形叫相似形；两个图形相似，其中一个图形可以看作由另一个图形的 或 ‎ ‎ 而得到的.‎ ‎3、下面各组中的两个图形， 是形状相同的图形， 是形状不同的图形.‎ 二、选择题 ‎1．（1）JL；（2）¬；（3）èé；（4）ÀÁ.‎ 在上述各种符号中，形状相同的符号有几组？ （ ）‎ A．一组 B．二组 C．三组 D．四组 ‎2．下列说法中，正确的是（　　　）‎ A．正方形与矩形的形状一定相同　　　　　B．两个直角三角形的形状一定相同 C．形状相同的两个图形的面积一定相等　　D．两个等腰直角三角形的形状一定相同 ‎3．经历平移、旋转、轴对称变化前后的两个图形　　（　　　）‎ A．形状大小都一样　　　　　B．形状一样，大小不一样　‎ C．形状不一样，大小一样　　D．形状大小都不一样 ‎4．在平面坐标系中，一个图形各点的横坐标、纵坐标都加上或减去同一个非零数，得到一组新的对应用点，则连接所得到点的图形与原图形形状（　　　）‎ A．不能够互相重合　　B．形状相同，大小也一定相同　　‎ C．形状不一样　　 　D．形状相同，大小不一定相同 三、解答题 画一个三角形，然后把它的各边扩大2倍，画出图形，观察新图形与原图形的关系.‎ 九年级数学图形的相似集体备课教案 8‎ ‎27.1图形的相似（第2课时）‎ ‎【教学任务分析】‎ 教 学 目 标 知识 技能 ‎1.了解比例线段的定义.‎ ‎2.掌握相似多边形的主要特征，即：相似多边形的对应角相等，对应边的比相等．‎ ‎3.会根据相似多边形的特征识别两个多边形是否相似，并会运用其性质进行相关的计算．‎ 过程 方法 经历相似图形的认识过程，观察相似图形的关系，得到相似多边形对应边成比例，对应角相等的性质 情感 态度 通过学生从图形相似的角度识别现实生活中存在的规律，培养合作交流意识．‎ 重点 相似多边形的性质.‎ 难点 运用相似多边形的特征进行相关的计算．‎ ‎【教学环节安排】‎ 环节 教 学 问 题 设 计 教学活动设计 问题最佳 解决方案 情 境 引 入 问题：如果把老师手中的教鞭与铅笔，分别看成是两条线段AB和CD，那么这两条线段的长度比是多少？‎ 归纳：两条线段的比，就是两条线段长度的比．‎ 问题：成比例线段：对于四条线段a,b,c,d，如果其中两条线段的比与另两条线段的比相等，如（即ad=bc），我们就说这四条线段是成比例线段，简称比例线段．‎ ‎【注意】 （1）两条线段的比与所采用的长度单位没有关系，在计算时要注意统一单位；（2）线段的比是一个没有单位的正数；（3）四条线段a,b,c,d成比例，记作或a:b=c:d；（4）若四条线段满足，则有ad=bc．‎ 教师出示问题 上节课学习了图形的相似的定义，并且能判断一些简单图形是否相似，今天继续探讨相似图形的特征，及判断方法.‎ 请同学们完成左边的问题.‎ 引入新课 自 主 如图27.1—4的左边格点图中有一个四边形，请在右边的格点图中画出一个与该四边形相似的图形．‎ 教师出示问题，学生作图，并观察思考下面的问题 8‎ 探 究 合 作 交 流 问题1. 对于图中两个相似的四边形，它们的对应角，对应边的比是否相等．‎ ‎【结论】：‎ ‎（1）相似多边形的特征：相似多边形的对应角相等，对应边的比相等．‎ 反之，如果两个多边形的对应角相等，对应边的比相等，那么这两个多边形相似．‎ ‎（2）相似比：相似多边形对应边的比称为相似比．‎ 问题2：相似比为1时，相似的两个图形有什么关系？‎ ‎【结论】：‎ 相似比为1时，相似的两个图形全等，因此全等形是一种特殊的相似形．‎ 教师巡视指导学生作图，并了解学生在作图中是不是出现全等的情况 学生小组讨论，得出结论.‎ ‎ ‎ 师生共同总结探究结论 教师板演 尝 试 应 用 例1下列说法正确的是（ ）‎ A．所有的平行四边形都相似 B．所有的矩形都相似 C．所有的菱形都相似 D．所有的正方形都相似 ‎【分析】：A中平行四边形各角不一定对应相等，因此所有的平行四边形不一定都相似，故A错；B中矩形虽然各角都相等，但是各对应边的比不一定相等，因此所有的矩形不一定都相似，故B错；C中菱形虽然各对应边的比相等，但是各角不一定对应相等，因此所有的菱形不一定都相似，故C也错；D中任两个正方形的各角都相等，且各边都对应成比例，因此所有的正方形都相似.‎ 例2如图27.1—5，四边形ABCD和EFGH相似，求角α、β的大小和EH的长度x。‎ 教师出示题目。小组讨论分析： 找出正确与错误的理由 教师点拨 教师出示例题 ‎ ‎ 学生独立思考，并列出相应的数量关系，写出解题过程 找两名同学板书 学生板书 8‎ ‎【分析】求相似多边形中的某些角的度数和某些线段的长，可根据相似多边形的对应角相等，对应边的比相等来解题，关键是找准对应角与对应边，从而列出正确的比例式．‎ 练习：课后练习1、2、3‎ 师巡视，个别指导。‎ 成果 展示 ‎1本节课我们都学习了哪些内容？‎ 相似图形的定义 判断相似图形 相似多边形的性质特征 ‎2．在学习的过程中,你有怎样的收获?‎ 教师提出问题。‎ 学生回顾本课内容，总结回答。‎ 教师适当板书，协助总结，并该强调的强调。‎ 补 偿 提 高 已知四边形ABCD与四边形A1B1C1D1相似，且A1B1:B1C1:C1D1:D1A1=7:8:11:14，若四边形ABCD的周长为40，求四边形ABCD的各边的长．‎ 学生讨论分析：因为两个四边形相似，因此可根据相似多边形的对应边的比相等来解题．‎ 一生板演 作业 设 计 必做题:‎ P38习题27·1题3、5‎ 选做题：‎ P38习题27·1题2、6‎ 教师布置作业，并提出要求.‎ 学生课下独立完成，延续课堂.‎ 教 后 反 思 8‎ ‎【当堂达标自测题】‎ 一、填空题 ‎1． 矩形ABCD中AB=CD=8,AD=BC=6,矩形EFGH中，EF=GH=3,EH=FG=4,这两个矩形_____ ‎ ‎2．△ABC的三条边之比为2：5：6，与其相似的另一个△A′B′C′最大边长为18cm，则另两边长的和为_______．‎ ‎3．两个相似三角形的一对对应边长分别为20cm，25cm，它们的周长差为63cm，则这两个三角形的周长分别是________．‎ ‎4. ΔABC与△DEF中，∠A=65°,∠B=42°,∠D=65°,∠F=73°,AB=3,AC=5,BC=6,DE=6,DF=10,EF=12,则△DEF 与△ABC_____‎ 二、选择题 ‎5．△ABC与△DEF相似，且相似比是，则△DEF 与△ABC与的相似比是（ ）．‎ A． B． C． D．‎ ‎6．下列所给的条件中，能确定相似的有（ ）‎ ‎（1）两个半径不相等的圆；（2）所有的正方形；（3）所有的等腰三角形；（4）所有的等边三角形；（5）所有的等腰梯形；（6）所有的正六边形．‎ A．3个 B．4个 C．5个 D．6个 ‎7．把mn=pq（mn≠0）写成比例式，写错的是（ ）‎ ‎ A． B． C． D．‎ ‎8．在一张比例尺为1：15000的平面图上，一块多边形地区的其中一边长为5cm，那么这块地区实际上和这一边相对应的长度应为（ ）‎ ‎ A．750cm B．75000cm C．3000cm D．300cm 三、解答题 ‎9．小红准备在一张宽16cm，长20cm的风景图片的四周镶上一条2cm宽的金色纸边，如图27.1—6问金色纸边的内外边缘所成的矩形相似吗？为什么？‎ ‎10．如图27.1—7，AB∥EF∥CD，CD=4，AB=9，若梯形CDEF与梯形EFAB相似，求EF的长．‎ 8‎