北师大版九年级上册数学第四章测试题及答案 9页

北师大版九年级上册数学第四章测试题及答案 ‎(考试时间：120分钟　　　满分：120分)‎ 第Ⅰ卷(选择题　18分)‎ 一、选择题(本大题共6小题，每小题3分，共18分)‎ ‎1．如果ab＝cd，那么下列式子不成立的是(　C　)‎ A.＝ B.＝ C.＝ D.＝ ‎2．下列几组图形：①两个等腰三角形；②两个直角三角形；③两个正方形；④两个矩形；⑤两个菱形；⑥两个正五边形．其中一定相似的有(　A　)‎ A．2组 B．3组 C．4组 D．5组 ‎3．已知＝＝，则的值是(　D　)‎ A．1或－1 B．－1或－2 C．2或1 D．2或－1‎ ‎4．(重庆中考)如图，在平行四边形ABCD中，点E在AD上，连接CE并延长与BA的延长线交于点F，若AE＝2ED，CD＝3 cm，则AF的长为(　B　)‎ A．5 cm B．6 cm C．7 cm D．8 cm ‎ ‎ 第4题图　 　 　第5题图 ‎5．(兰州中考)如图，小明为了测量一凉亭的高度AB(顶端A到水平地面BD的距离)，在凉亭的旁边放置一个与凉亭台阶BC等高平台DE(DE＝BC＝0.5米，A，C，B三点共线)，把一面镜子水平放置在平台上的点G处，测得CG＝15米，然后沿直线CG后退到点E处，这时恰好在镜子里看到凉亭的顶端A，测得GE＝3米，小明身高EF＝1.6米，则凉亭的高度AB约为(　A　)‎ A．8.5米 B．9米 C．9.5米 D．10米 ‎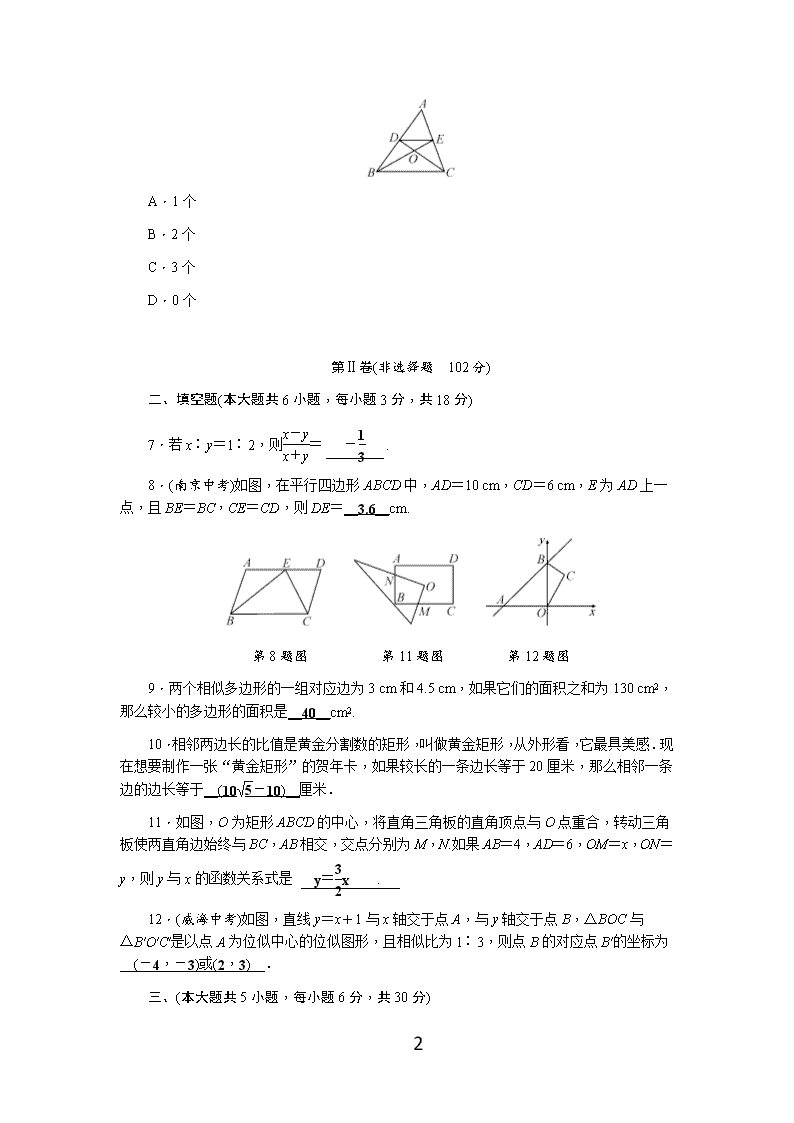6．如图，在△ABC中，中线BE，CD相交于点O，连接DE，下列结论：①＝；②＝；③＝.其中正确的个数有(　B　)‎ 9‎ A．1个 B．2个 C．3个 D．0个 第Ⅱ卷(非选择题　102分)‎ 二、填空题(本大题共6小题，每小题3分，共18分)‎ ‎7．若x∶y＝1∶2，则＝ － .‎ ‎8．(南京中考)如图，在平行四边形ABCD中，AD＝10 cm，CD＝6 cm，E为AD上一点，且BE＝BC，CE＝CD，则DE＝__3.6__cm.‎ ‎ ‎ 第8题图　 　 第11题图　 　第12题图 ‎9．两个相似多边形的一组对应边为3 cm和4.5 cm，如果它们的面积之和为130 cm2，那么较小的多边形的面积是__40__cm2.‎ ‎10．相邻两边长的比值是黄金分割数的矩形，叫做黄金矩形，从外形看，它最具美感．现在想要制作一张“黄金矩形”的贺年卡，如果较长的一条边长等于20厘米，那么相邻一条边的边长等于__(10－10)__厘米．‎ ‎11．如图，O为矩形ABCD的中心，将直角三角板的直角顶点与O点重合，转动三角板使两直角边始终与BC，AB相交，交点分别为M，N.如果AB＝4，AD＝6，OM＝x，ON＝y，则y与x的函数关系式是 y＝x .‎ ‎12．(威海中考)如图，直线y＝x＋1与x轴交于点A，与y轴交于点B，△BOC与△B′O′C′是以点A为位似中心的位似图形，且相似比为1∶3，则点B的对应点B′的坐标为__(－4，－3)或(2，3)__．‎ 三、(本大题共5小题，每小题6分，共30分)‎ 9‎ ‎13．已知a，b，c是△ABC的三边，＝＝，且a＋b＋c＝12，试判断△ABC的形状．‎ 解：设＝＝＝k(k≠0)，‎ 则a＝3k－4，b＝2k－3，c＝4k－8，‎ ‎∵a＋b＋c＝12，∴3k－4＋2k－3＋4k－8＝12，解得k＝3.‎ ‎∴a＝3k－4＝5，b＝2k－3＝3，c＝4k－8＝4.‎ ‎∵b2＋c2＝9＋16＝25，a2＝25，‎ ‎∴△ABC为直角三角形．‎ ‎14.如图，AB＝25，BC＝40，AC＝20，AE＝12，AD＝15，DE＝24.‎ ‎(1)判断△ABC与△AED是否相似；‎ ‎(2)若∠BAC＝100°，∠EAC＝70°，求∠CAD的度数．‎ 解：(1)∵＝，＝，＝，‎ ‎∴△ABC∽△ADE.‎ ‎(2)∵△ABC∽△ADE，∴∠DAE＝∠BAC＝100°.‎ 又∵∠EAC＝70°，∴∠CAD＝30°.‎ ‎15．如图，已知直线l1，l2，l3分别交直线l4于点A，B，C，交直线l5于点D，E，F，且l1∥l2∥l3.‎ ‎(1)若AB＝4，BC＝8，EF＝12，求DE的长；‎ ‎(2)若DE∶EF＝2∶3，AB＝6，求AC的长．‎ 9‎ 解：(1)∵l1∥l2∥l3，∴＝＝＝，‎ ‎∴DE＝EF＝6；‎ ‎(2)∵l1∥l2∥l3，∴＝＝，‎ ‎∴BC＝AB＝× 6＝9，‎ ‎∴AC＝AB＋BC＝6＋9＝15.‎ ‎16．已知两个相似多边形的一对对应边的边长分别是15 cm和12 cm.‎ ‎(1)若它们的周长相差24 cm，求这两个多边形的周长；‎ ‎(2)若它们的面积差270 cm2，求这两个多边形的面积．‎ 解：(1)设较小多边形的周长为x cm，‎ 则较大多边形的周长为(x＋24)cm，‎ 由题意得＝，解得x＝96，∴x＋24＝120.‎ 所以较小多边形的周长为96 cm，较大多边形的周长为120 cm；‎ ‎(2)设较小多边形的面积为x cm2，‎ 则较大多边形的面积为(x＋270)cm2，‎ 由题意得＝，解得x＝480，∴x＋270＝750.‎ 所以较小多边形的面积为480 cm2，较大多边形的面积为750 cm2.‎ 9‎ ‎17.(无锡中考)下图小方格是边长为1的正方形，△ABC与△A1B1C1是关于点O为位似中心的位似图形，它们的顶点都在小正方形的顶点上．‎ ‎(1)画出位似中心O；‎ ‎(2)求△ABC与△A1B1C1的相似比．‎ 解：(1)如图所示；‎ ‎(2)A1B1＝，AB＝2，则△ABC与△A1B1C1的相似比为2.‎ 四、(本大题共3小题，每小题8分，共24分)‎ ‎18．已知：如图，在正方形ABCD中，P是BC上的点，且BP＝3PC，Q是CD的中点．求证：‎ ‎(1)△ADQ∽△QCP；‎ ‎(2)AQ⊥PQ.‎ 证明：(1)设PC＝a，Q是CD的中点．‎ ‎∵BP＝3PC，∴AD＝4a，QC＝DQ＝2a.‎ ‎∵＝＝2，＝＝2.‎ 又∵∠D＝∠C＝90°，∴△ADQ∽△QCP；‎ ‎(2)∵△ADQ∽△QCP，∴∠1＝∠2，‎ ‎∵∠2＋∠3＝90°，∴∠1＋∠3＝90°，‎ ‎∴∠AQP＝180°－(∠1＋∠3)＝180°－90°＝90°，‎ ‎∴AQ⊥PQ.‎ 9‎ ‎19．如图，△ABC和△BEC均为等腰直角三角形，且∠ACB＝∠BEC＝90°，AC＝4，点P为线段BE延长线上一点，连接CP以CP为直角边向下作等腰直角△CPD，线段BE与CD相交于点F.‎ ‎(1)求证：＝；‎ ‎(2)连接BD，请你判断AC与BD有什么位置关系？并说明理由．‎ ‎(1)证明：△BCE和△CDP均为等腰直角三角形，‎ ‎∴∠ECB＝∠PCD＝45°，∠CEB＝∠CPD＝90°，‎ ‎∴△BCE∽△DCP，∴＝.‎ ‎(2)解：AC∥BD，理由如下：‎ ‎∵∠PCE＋∠ECD＝∠BCD＋∠ECD＝45°，∴∠PCE＝∠BCD，‎ 又∵＝，∴△PCE∽△DCB，∴∠CBD＝∠CEP＝90°，‎ ‎∵∠ACB＝90°，∴∠ACB＝∠CBD，∴AC∥BD.‎ ‎20．如图，在△ABC中，点D，E分别在边AB，AC上，∠AED＝∠B.射线AG分别交线段DE，BC于点F，G，且＝.‎ ‎(1)求证：△ADF∽△ACG；‎ ‎(2)若＝，求的值．‎ ‎(1)证明：∵∠AED＝∠B，∠DAE＝∠CAB，‎ 9‎ ‎∴∠ADF＝∠C，又∵＝，‎ ‎∴△ADF∽△ACG.‎ ‎(2)解：∵△ADF∽△ACG，∴＝，‎ 又∵＝，∴＝，∴＝1.‎ 五、(本大题共2小题，每小题9分，共18分)‎ ‎21．如图所示，在高5 m的房顶上A处望一幢楼的底部D，视线过小树的顶端E，又从房底部B处望楼顶C，视线也正好过小树顶端E，测得小树的高度为4 m，则你能算出楼CD的高吗？把你的计算过程写出来．‎ 解：由EF∥AB∥CD，∴ ‎∴由①＋②，得＋＝＋＝1，‎ ‎∴＋＝1，∴DC＝20 m.‎ ‎22．如图，在正方形ABCD中，E是BC上的一点，连接AE，作BF⊥AE，垂足为H，交CD于F，作CG∥AE，交BF于G.‎ 求证：(1)CG＝BH；‎ 9‎ ‎(2)FC2＝BF·GF.‎ 证明：(1)∵BF⊥AE，CG∥AE，∴CG⊥BF.‎ ‎∵在正方形ABCD中，∠ABH＋∠CBG＝90°，‎ ‎∠CBG＋∠BCG＝90°，∠BAH＋∠ABH＝90°，‎ ‎∴∠BAH＝∠CBG，∠ABH＝∠BCG，AB＝BC，‎ ‎∴△ABH≌△BCG，∴CG＝BH.‎ ‎(2)∵∠BFC＝∠CFG，∠BCF＝∠CGF＝90°，‎ ‎∴△CFG∽△BFC，∴＝，即FC2＝BF·GF.‎ 六、(本大题共12分)‎ ‎23．如图，在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，点D为边CB上的一个动点(点D不与点B重合)，过D作DO⊥AB，垂足为O，点B′在边AB上，且与点B关于直线DO对称，连接DB′，AD.‎ ‎(1)求证：△DOB∽△ACB；‎ ‎(2)若AD平分∠CAB，求线段BD的长；‎ ‎(3)当△AB′D为等腰三角形，求线段BD的长．‎ ‎(1)证明：∵DO⊥AB，∴∠DOB＝∠DOA＝90°，‎ ‎∴∠DOB＝∠ACB＝90°，‎ 又∵∠B＝∠B，∴△DOB∽△ACB.‎ ‎(2)解：∵∠ACB＝90°，‎ ‎∴AB＝＝＝10，‎ ‎∵AD平分∠CAB，DC⊥AC，DO⊥AB，∴DC＝DO，‎ 在Rt△ACD和Rt△AOD中， ‎∴Rt△ACD≌△Rt△AOD(HL)，‎ 9‎ ‎∴AC＝AO＝6，设BD＝x，则DC＝DO＝8－x，OB＝AB－AO＝4，‎ 在Rt△BOD中，根据勾股定理得DO2＋OB2＝BD2，‎ 即(8－x)2＋42＝x2，解得x＝5，∴BD的长为5.‎ ‎(3)解：∵点B′与点B关于直线DO对称，‎ ‎∴∠B＝∠OB′D，BO＝B′O，BD＝B′D，‎ ‎∵∠B为锐角，∴∠OB′D也为锐角，∴∠AB′D为钝角，‎ ‎∴当△AB′D为等腰三角形时，AB′＝DB′，‎ ‎∵△DOB∽△ACB，∴＝＝＝，‎ 设BD＝5x，则AB′＝DB′＝5x，BO＝B′O＝4x，‎ ‎∵AB′＋B′O＋BO＝AB，∴5x＋4x＋4x＝10，解得x＝，‎ ‎∴BD＝.‎ 9‎