2020年中考数学一轮复习基础点专题01有理数含解析 21页

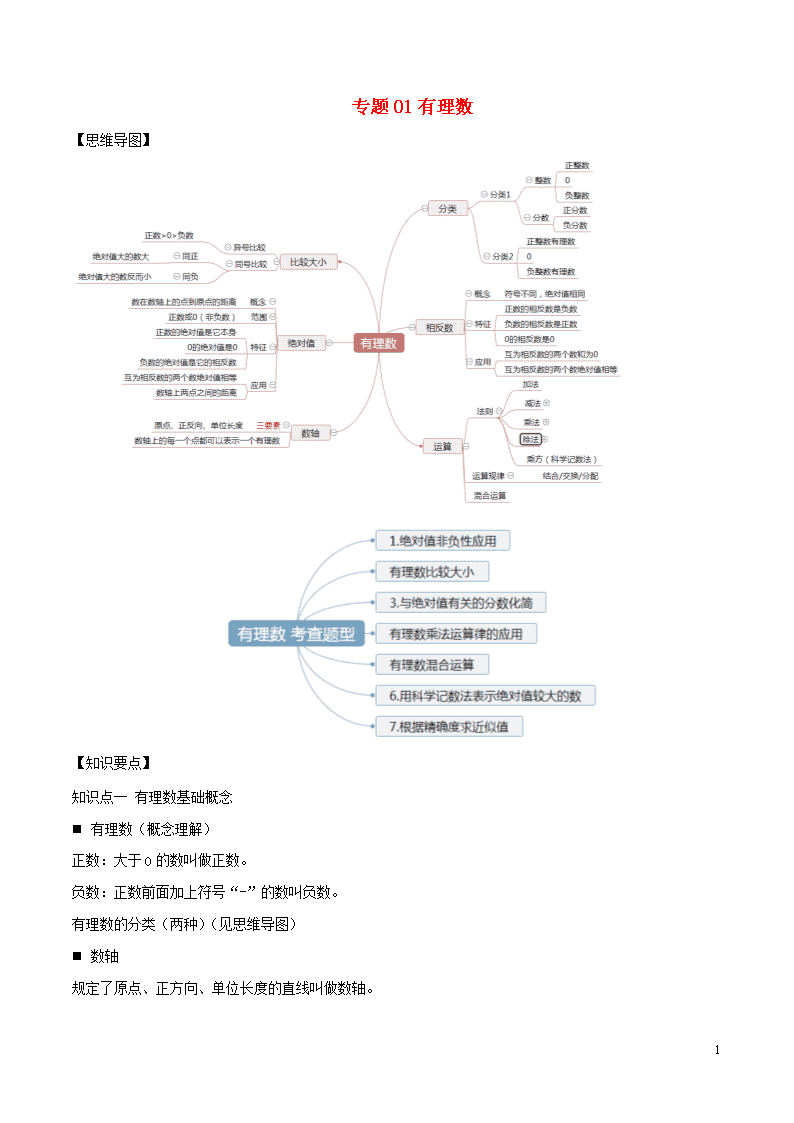
专题01有理数 ‎【思维导图】‎ ‎【知识要点】‎ 知识点一 有理数基础概念 n 有理数（概念理解）‎ 正数：大于0的数叫做正数。‎ 负数：正数前面加上符号“-”的数叫负数。‎ 有理数的分类（两种）（见思维导图）‎ n 数轴 ‎ 规定了原点、正方向、单位长度的直线叫做数轴。‎ 21‎ ü 数轴的三要素：原点、正方向、单位长度（重点）‎ 任何有理数都可以用数轴上的点表示，有理数与数轴上的点是一一对应的。‎ ü 数轴上的点表示的数从左到右依次增大；原点左边的数是负数，原点右边的数是正数.‎ ‎【注意】‎ 1. 数轴是一条直线，可向两段无限延伸。‎ 2. 在数轴上原点，正方向，单位长度的选取需根据实际情况而定。‎ n 相反数 只有符号不同的两个数叫做互为相反数.（绝对值相等，符号不同的两个数叫做互为相反数）‎ n 绝对值 绝对值的概念：一班数轴上表示a的数与原点之间的距离叫做数a的绝对值。‎ 绝对值的意义：‎ 正数的绝对值是它本身；‎ 负数的绝对值是它的相反数；‎ ‎0的绝对值是0。‎ ‎（互为相反数的两个数的绝对值相等。）‎ n 比较大小 ‎1）数轴上两个点表示的数，右边的总比左边的大。‎ ‎2）正数大于0，负数小于0，正数大于负数。‎ ‎3）两个负数比较，绝对值大的反而小。‎ ‎4）两个正数比较，绝对值大的反而大。‎ 常用方法：数轴比较法、差值比较法、商值比较法、绝对值比较法等。‎ ‎1．（2018·海南琼山中学中考模拟）下列各组数中，互为相反数的是 ( )‎ A．|+2|与|-2| B．-|+2|与+(-2) C．-(-2)与+(+2) D．|-(-3) |与-|-3|‎ ‎【详解】‎ 解：A、|+2|=2，|-2|=2，故这两个数相等，故此选项错误； B、-|+2|=-2，+（-2）=-2，故这两个数相等，故此选项错误； C、-（-2）=2与+（+2）=2，这两个数相等，故此选项错误； D、|-（-3）|=3，-|-3|=-3，3+（-3）=0，这两个数互为相反数，故此选项正确． 故选：D．‎ 21‎ ‎2．（2019·四川中考真题）一定是 A．正数 B．负数 C． D．以上选项都不正确 ‎【详解】‎ ‎∵a可正、可负、也可能是0‎ ‎∴选D.‎ ‎3．（2018·内蒙古中考模拟）如图，在数轴上表示互为相反数的两数的点是（　　）‎ A．点A和点C B．点B和点C C．点A和点B D．点B和点D ‎【详解】‎ A、B、C、D所表示的数分别是2，1，-2，-3，因为2和-2互为相反数，故选A．‎ ‎4．（2013·江苏中考真题）如图，数轴上的点A、B分别对应实数a、b，下列结论中正确的是（ ）‎ A．a＞b B．|a|＞|b| C．﹣a＜b D．a+b＜0‎ ‎【详解】‎ 根据数轴，a＜0，b＞0，且|a|＜|b|，‎ A、应为a＜b，故本选项错误；‎ B、应为|a|＜|b|，故本选项错误；‎ C、∵a＜0，b＞0，且|a|＜|b|，∴a+b＞0，∴﹣a＜b正确，故本选项正确；‎ D、应该是a+b＞0，故本选项错误．‎ 故选C．‎ ‎5．（2019·甘肃中考真题）已知，是2的相反数，则的值为(　　)‎ A．-3 B．-1 C．-1或-3 D．1或-3‎ ‎【详解】‎ ‎∵，是2的相反数，‎ ‎∴或，，‎ 当时，；‎ 当时，；‎ 21‎ 综上，的值为-1或-3，‎ 故选：C．‎ 考察题型一 绝对值非负性应用 ‎1．（2016·山东中考真题）当1|a|,故②错误，因为b<0a+b，所以④正确.‎ 故选：B.‎ ‎4．（2018·湖北中考真题）在0，﹣1，0.5，（﹣1）2四个数中，最小的数是（　　）‎ A．0 B．﹣1 C．0.5 D．（﹣1）2‎ ‎【详解】根据有理数比较大小的方法，可得 ‎﹣1＜0＜0.5＜（﹣1）2，‎ ‎∴在0，﹣1，0.5，（﹣1）2四个数中，最小的数是﹣1．‎ 故选B．‎ ‎5．（2018·山东中考真题）实数a，b，c，d在数轴上的位置如图所示，下列关系式不正确的是（　　）‎ A．|a|＞|b| B．|ac|=ac C．b＜d D．c+d＞0‎ ‎【详解】‎ 从a、b、c、d在数轴上的位置可知：a＜b＜0，d＞c＞1；‎ A、|a|＞|b|，故选项正确；‎ B、a、c异号，则|ac|=-ac，故选项错误；‎ C、b＜d，故选项正确；‎ D、d＞c＞1，则a+d＞0，故选项正确．‎ 故选：B.‎ 知识点二 有理数四则运算 n 有理数的加法（重点）‎ 有理数的加法法则：（先确定符号，再算绝对值）‎ ‎1.同号两数相加，取相同的符号，并把绝对值相加；‎ ‎2.异号两数相加，绝对值不相等时，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值；‎ ‎3.互为相反数的两个数相加得0；（如果两个数的和为0，那么这两个数互为相反数）‎ ‎4.一个数同0相加，仍得这个数。‎ 有理数的加法运算律：‎ 加法交换律：两个数相加，交换加数的位置，和不变。‎ 即；‎ 加法结合律：三个数相加，先把前两个数相加，或者先把后两个数相加，和不变。‎ 21‎ 即。‎ n 有理数的减法 有理数的减法法则：‎ 减去一个数等于加上这个数的相反数。即。‎ 注：两个变化：减号变成加号；减数变成它的相反数。‎ n 有理数的加减混合运算 规则：运用减法法则将加减混合运算统一为加法进行运算 步骤：（1）减法化加法；‎ ‎ （2）省略括号和加号；‎ ‎ （3）运用加法运算律使计算简便；‎ ‎ （4）运用有理数加法法则进行计算。‎ ‎ 注：运用加法运算律时，可按如下几点进行：‎ ‎（1）同号的先结合；‎ ‎（2）同分母的分数或者比较容易通分的分数相结合；‎ ‎（3）互为相反数的两数相结合；‎ ‎（4）能凑成整数的两数相结合；‎ ‎（5）带分数一般化为假分数或者分为整数和分数两部分，再分别相加。‎ n 有理数的乘法（重点）‎ 有理数的乘法法则：‎ ‎（1）两数相乘，同号得正，异号得负，并把绝对值相乘。‎ ‎（2）任何数同0相乘，都得0.‎ 倒数：乘积是1的两个有理数互为倒数。0没有倒数。（数的倒数是）‎ 多个有理数相乘的法则及规律：‎ （1） 几个不是0的数相乘，负因数的个数是奇数时，积是负数； ‎ 负因数的个数是偶数时，积是正数。‎ 确定符号后，把各个因数的绝对值相乘。‎ ‎（2）几个数相乘，有一个因数为0，积为0；反之，如果积为0，那么至少有一个因数是0.‎ 21‎ 注：带分数与分数相乘时，通常把带分数化成假分数，再与分数相乘。‎ n 有理数的乘法运算律 乘法交换律：两个数相乘，交换因数的位置，积相等。‎ 即。‎ 乘法结合律：三个数相乘，先把前两个数相乘，或者先把后两个数相乘，积相等。‎ 即。‎ 乘法分配律：一个数同两个数的和相乘，等于把这个数分别同这两个数相乘，再把积相加。‎ 即。‎ n 有理数的除法 有理数除法法则：‎ ‎（1）除以一个不为0的数，等于乘以这个数的倒数。即。‎ ‎（2）两数相除（被除数不为0），同号得正，异号得负，并把绝对值相除。‎ ‎0除以任何不为0的数，都得0。‎ 步骤：先确定商的符号，再算出商的绝对值。‎ n 有理数的乘除混合运算 运算顺序：从左往右进行，将除法化成乘法后，进行约分计算。‎ ‎（注：带分数应首先化为假分数进行运算）‎ n 有理数的四则混合运算 运算顺序：先乘除，后加减，有括号要先算括号里面的。‎ 注：除法一般先化为乘法，带分数化为假分数，合理使用运算律 ‎1．（2018·江苏中考模拟）计算：|–5+3|的结果是（ ）‎ A．–8 B．8 C．–2 D．2‎ ‎【解析】‎ 原式=|-2|=2，‎ 故选：D．‎ ‎2.（2019·浙江中考真题）某地一周前四天每天的最高气温与最低气温如右表，则这四天中温差最大的是（ ）‎ 21‎ 星期 一 二 三 四 最高气温 ‎10℃‎ ‎12℃‎ ‎11℃‎ ‎9℃‎ 最低气温 ‎3℃‎ ‎0℃‎ ‎-2℃‎ ‎-3℃‎ A．星期一 B．星期二 C．星期三 D．星期四 ‎【详解】‎ 星期一温差：10﹣3＝7℃；‎ 星期二温差：12﹣0＝12℃；‎ 星期三温差：11﹣（﹣2）＝13℃；‎ 星期四温差：9﹣（﹣3）＝12℃；‎ 综上，周三的温差最大.‎ 故选C．‎ ‎3．（2018·四川中考模拟）如果a，b是有理数，那么下列各式中成立的是（ ）‎ A．如果a<0，b<0，那么a＋b>0 B．如果a>0，b<0，那么a＋b>0‎ C．如果a>0，b<0，那么a＋b<0 D．如果a>0，b<0，且|a|>|b|，那么a＋b>0‎ ‎【解析】‎ 解：A、∵同号两数相加取与加数相同的符号，∴a+b<0,故选项错误；‎ B、如a=1,b=-2时，a+b=-1<0，故选项错误；‎ C、如a=3,b=-2时，a+b＝１>0，故选项错误；‎ D、异号两数相加，取绝对值较大数的符号，并用较大的绝对值减去较小的绝对值，故选项正确．‎ 故选D．‎ ‎4．（2019·辽宁中考模拟）计算的正确结果是（　　）‎ A． B．- C．1 D．﹣1‎ ‎【详解】‎ 原式 故选：D.‎ ‎5．（2017·山东中考真题）计算－(－1)＋|－1|，其结果为( )‎ 21‎ A．－2 B．2 C．0 D．－1‎ ‎【解析】‎ 试题分析：由题可得：原式=1+1=2，‎ 故选：B．‎ ‎6．（2018·辽宁中考模拟）两个非零有理数的和为零，则它们的商是（　　）‎ A．﹣1 B．0 C．1 D．﹣1或1‎ ‎【详解】‎ ‎∵两个非零有理数的和为零，‎ ‎∴这两个数是一对相反数，‎ ‎∴它们符号不同，绝对值相等，‎ ‎∴它们的商是-1，‎ 故选A．‎ ‎7．（2019·内蒙古中考模拟）若‎-‎‎1‎‎2‎的倒数与m+4‎互为相反数，则m的值是（ ）‎ A．1 B．‎-1‎ C．2 D．‎‎-2‎ ‎【详解】‎ ‎-‎‎1‎‎2‎的倒数与m+4互为相反数，得 m+4=2，‎ 解得m=−2，‎ 故选：D.‎ ‎8．（2018·天津中考模拟）-6÷的结果等于（　　）‎ A．1 B．﹣1 C．36 D．﹣36‎ ‎【详解】‎ 解：原式=﹣6×6=﹣36‎ 故选：D．‎ ‎8．（2019·平阳县鳌江中学中考模拟）－2×（－5）的值是　　‎ A．－7 B．7 C．－10 D．10‎ ‎【详解】‎ ‎﹣2×（﹣5）=+(2×5)=10.‎ 21‎ 故选D.‎ ‎9．（2019·天津中考模拟）计算（–18）÷（–6）的结果等于 A．3 B．–3 C． D．−‎ ‎【详解】‎ ‎=3‎ 考查题型三 与绝对值有关的分数化简 ‎1．（2018·福建中考模拟）若a≠0，b≠0，则代数式的取值共有（　　）‎ A．2个 B．3个 C．4个 D．5个 ‎【详解】‎ 由分析知：可分4种情况：‎ ‎①a＞0，b＞0，此时ab＞0，‎ 所以=1+1+1=3；‎ ‎②a＞0，b＜0，此时ab＜0，‎ 所以=1﹣1﹣1=﹣1；‎ ‎③a＜0，b＜0，此时ab＞0，‎ 所以=﹣1﹣1+1=﹣1；‎ ‎④a＜0，b＞0，此时ab＜0，‎ 所以=﹣1+1﹣1=﹣1；‎ 综合①②③④可知：代数式的值为3或﹣1，‎ 故选A．‎ ‎2．（2018·南宫市奋飞中学中考模拟）已知a，b，c为非零的实数，则的可能值的个数为（　　）‎ 21‎ A．4 B．5 C．6 D．7‎ ‎【解析】‎ 解：①a、b、c三个数都是正数时，a＞0，ab＞0，ac＞0，bc＞0，原式=1+1+1+1=4；‎ ‎②a、b、c中有两个正数时，设为a＞0，b＞0，c＜0，则ab＞0，ac＜0，bc＜0，原式=1+1﹣1﹣1=0；‎ 设为a＞0，b＜0，c＞0，则ab＜0，ac＞0，bc＜0，原式=1﹣1+1﹣1=0；‎ 设为a＜0，b＞0，c＞0，则ab＜0，ac＜0，bc＞0，原式=﹣1﹣1﹣1+1=﹣2；‎ ‎③a、b、c有一个正数时，设为a＞0，b＜0，c＜0，则ab＜0，ac＜0，bc＞0，原式=1﹣1﹣1+1=0；‎ 设为a＜0，b＞0，c＜0，则ab＜0，ac＞0，bc＜0，原式=﹣1﹣1+1﹣1=﹣2；‎ 设为a＜0，b＜0，c＞0，则ab＞0，ac＜0，bc＜0，原式=﹣1+1﹣1﹣1=﹣2；‎ ‎④a、b、c三个数都是负数时，即a＜0，b＜0，c＜0，则ab＞0，ac＞0，bc＞0，原式=﹣1+1+1+1=2．‎ 综上所述：的可能值的个数为4．‎ 故选A．‎ ‎3.．（2019·四川初一期中）有理数a，b．c满足abc＜0，的值为（　）‎ A．1或﹣3 B．﹣4 C．0 D．0或﹣4‎ ‎【详解】‎ 解：∵abc＜0，‎ ‎∴当有理数a，b，c中有一个数小于0时，，‎ 当有理数a，b，c中三个数都小于0时，，‎ 故选：D．‎ 考察题型四 有理数乘法运算律的应用 ‎1．（2018·贵州中考真题）计算+++++……+的值为（　　）‎ A． B． C． D．‎ ‎【解析】‎ 原式=‎ 21‎ ‎=，‎ ‎=1-‎ ‎=． 故选：B．‎ ‎2．（2019·河北中考模拟）利用运算律简便计算52×（–999）+49×（–999）+999正确的是 A．–999×（52+49）=–999×101=–100899‎ B．–999×（52+49–1）=–999×100=–99900‎ C．–999×（52+49+1）=–999×102=–101898‎ D．–999×（52+49–99）=–999×2=–1998‎ ‎【详解】‎ 原式=－999×（52+49-1）=－999×100=－99900．‎ 故选B ‎3．（2016·河北中考真题）请你参考黑板中老师的讲解，用运算律简便计算：‎ ‎（1）999×（-15）；‎ ‎（2）999×+999×（）-999×.‎ ‎【详解】‎ 试题分析：根据题目中所给的规律，第一题凑整法，第二题提同数法解决即可.‎ 试题解析：（1）999×（-15）=（1000-1）×（-15）=15-15000=149985;‎ ‎（2）999×+999×（）-999×=999×[+（）-]=999×100=99900.‎ 知识点三 有理数的乘方 n 乘方（重点）‎ 一般地，个相同的因数相乘，即a×a×a⋯×an个，记作，读作的次方。求个相同因 21‎ 数的积的运算，叫做乘方，乘方的结果叫做幂。‎ 在中，叫做底数，叫做指数。读作的次方，也可以读作的次幂。‎ 当底数为分数时，要先用括号将底数括上，再在其右上角写指数，指数要写的小些。‎ 乘方的规律：‎ 负数的奇次幂是负数，负数的偶次幂是正数。‎ 正数的任何次幂都是正数，0的任何正整数次幂都是0.‎ 有理数乘方的运算方法：‎ 1. 根据乘方的符号规律确定结果的符号。‎ 2. 计算结果的绝对值。‎ n 有理数的混合运算 运算顺序：（1）先乘方，再乘除，最后加减；‎ ‎（2）同级运算,从左到右进行；‎ ‎（3）如有括号，先算括号里的，按小括号、中括号、大括号的顺序。‎ n 科学记数法 把一个大于10的数记成的形式，其中是整数数位只有一位的数（即），是正整数，这样的记数方法叫科学记数法。（用科学记数法表示一个数时，10的指数比原数的整数位数少1.）‎ 把还原成原数时，只需把的小数点往前移动位。‎ n 近似数和有效数字 在实际问题中，由“四舍五入”得到的数或大约估计的数都是近似数。（近似数小数点后的末位数是0的，不能去掉0.）‎ 一个近似数从左边第一位非0的数字起，到末位数字止，所有的数字都是这个数的有效数字。一个近似数有几个有效数字，就称这个近似数保留几个有效数字。‎ 精确度：表示一个近似数与准确数的接近程度。一个近似数，四舍五入到哪一位，就称这个数精确到哪一位。‎ ‎1．（2018·丹东第九中学中考模拟）下列算式中，运算结果为负数的是( )‎ A．|-1| B．(-2)3 C．(-1)×(-2) D．(-3)2‎ ‎【解析】‎ 本题涉及乘法、绝对值、乘方等知识点．在计算时，需要针对每个知识点分别进行计算．‎ 21‎ 详解：A.|−1|＝1，错误；‎ B.(-2)3＝−8，正确；‎ C.（−1）×（−2）＝2，错误；‎ D.(-3)2＝9，错误；‎ 故选：B．‎ ‎2．（2018·四川成都外国语学校中考模拟）下列各数|﹣2|，﹣（﹣2）2，﹣（﹣2），（﹣2）3中，负数的个数有（　　）‎ A．1个 B．2个 C．3个 D．4个 ‎【详解】‎ 解：|﹣2|＝2，‎ ‎﹣（﹣2）2＝﹣4，‎ ‎﹣（﹣2）＝2，‎ ‎（﹣2）3＝﹣8，‎ ‎﹣4，﹣8是负数，‎ ‎∴负数有2个．‎ 故选：B．‎ ‎3.（2018·河南中考模拟）若a=﹣4×4，b=﹣|﹣32×1|，c=﹣5+2（﹣22），则a、b、c的大小关系是（　　）‎ A．a＞b＞c B．c＞b＞a C．b＞c＞a D．c＞a＞b ‎【详解】‎ 因为a=﹣4×4=-16，b=﹣|﹣32×1|=-15，c=﹣5+2（﹣22）=-13.‎ ‎-13>-15>-16.‎ 所以c＞b＞a 故选：B 考查题型五 有理数混合运算 ‎1．（2018·湖北中考模拟）计算：‎ ‎（1）5-（-2）+（-3）-（+4）；‎ ‎（2）（-）×（-24）；‎ 21‎ ‎（3）（-3）÷××（-15）；‎ ‎（4）-14+|（-2）3-10|-（-3）÷（-1）2017．‎ ‎【详解】‎ 解：（1）原式=5+2﹣3﹣4‎ ‎=5﹣3+2﹣4‎ ‎=2﹣2‎ ‎=0；‎ ‎（2）原式=×24+×24﹣×24‎ ‎=18+15﹣18‎ ‎=15；‎ ‎（3）原式=（﹣3）×××（﹣15）‎ ‎=4×4×5‎ ‎=80；‎ ‎（4）原式=﹣1+|﹣8﹣10|﹣（﹣3）÷（﹣1）‎ ‎=﹣1+18﹣3‎ ‎=14．‎ ‎2．（2018·湖北中考模拟）计算：‎ ‎（1）﹣15+（﹣8）﹣（﹣11）﹣12 ‎ ‎（2）‎ ‎（3）‎ ‎（4）﹣23+[（﹣4）2﹣（1﹣32）×3]‎ ‎【详解】‎ 原式 ‎.‎ 21‎ ‎（2）原式 ‎（3）原式 ‎，‎ ‎，‎ ‎（4）原式 ‎=32．‎ ‎3．（2018·海南琼山中学中考模拟）‎ ‎【详解】‎ 原式 考查题型六 用科学记数法表示绝对值较大的数 ‎1．（2019·河南郑州实验外国语中学中考模拟）我国倡导的“一带一路”建设将促进我国与世界一些国家的互利合作，根据规划“一带一路”地区覆盖总 人口为4400000000人，这个数用科学记数法表示为　　‎ A．44×108 B．4.4×108 C．4.4×109 D．4.4×1010‎ ‎【详解】‎ 解：4 400 000 000=4.4×109，‎ 21‎ 故选C．‎ ‎2．（2018·河南中考真题）今年一季度，河南省对“一带一路”沿线国家进出口总额达214.7亿元，数据“214.7亿”用科学记数法表示为（　　）‎ A．2.147×102 B．0.2147×103 C．2.147×1010 D．0.2147×1011‎ ‎【解析】‎ ‎214.7亿，用科学记数法表示为2.147×1010，‎ 故选：C．‎ ‎3.（2019·安徽中考模拟）据资料显示，地球的海洋面积约为360000000平方千米，请用科学记数法表示地球海洋面积面积约为多少平方千米( )‎ A． B． C． D．‎ ‎【解析】‎ 详解：将360000000用科学记数法表示为：3.6×108．‎ 故选：B．‎ ‎4．（2018·广东中考真题）260000000用科学计数法表示为( )‎ A． B． C． D．‎ ‎【详解】260000000的小数点向左移动8位得到2.6，‎ 所以260000000用科学记数法表示为，‎ 故选B.‎ ‎5．（2019·山东中考模拟）一个整数815550…0用科学记数法表示为8.1555×1010，则原数中“0”的个数为（　　）‎ A．4 B．6 C．7 D．10‎ ‎【详解】∵8.1555×1010表示的原数为81555000000，‎ ‎∴原数中“0”的个数为6，‎ 故选B．‎ 考查题型七 根据精确度求近似值 ‎1．（2018·山东中考模拟）近似数3.02×106精确到（　　）‎ A．百分位 B．百位 C．千位 D．万位 ‎【解析】‎ 近似数3.02×106精确到万位．‎ 21‎ 故选D．‎ ‎2．（2017·安徽中考模拟）用四舍五入法得到近似数4.005万，关于这个数有下列说法，其中正确的是（　　）‎ A．它精确到万位 B．它精确到0.001‎ C．它精确到万分位 D．它精确到十位 ‎【解析】‎ 近似数4.005万精确到十位．‎ 故选D．‎ ‎3．（2019·山东中考模拟）近似数1.23×103精确到（　　）‎ A．百分位 B．十分位 C．个位 D．十位 ‎【详解】‎ ‎∵1.23×103=1 230，‎ ‎∴这个近似数精确到十位．‎ 故选D．‎ ‎4．（2019·福建中考模拟）30269精确到百位的近似数是( )‎ A．303 B．30300 C． D．‎ ‎【详解】‎ 本题考查近似数的概念，按要求对30269取近似值，30269精确到百位的近似数应是303百，选项A明显错误，B选项精确到个位，C选项不是科学记数法的模型，D选项精确到百位，而且是规范的科学记数法.‎ 故选:D.‎ ‎5．（2019·四川中考真题）用四舍五入法将精确到千位，正确的是（ ）‎ A． B． C． D．‎ ‎【详解】‎ 解：130542精确到千位是1.31×105．‎ 故选：C．‎ ‎6．（2019·河北中考模拟）近似数5.10精确到（ ）‎ A．个位 B．十分位 C．百分位 D．十位 ‎【详解】‎ 解：5.10精确到百分位． 故选：C．‎ 21‎ ‎7．（2018·江苏中考模拟）今年无锡马拉松参赛选手91879人，这个数据精确到千位并用科学记数法表示为（　　）‎ A．91×103 B．92×103 C．9.1×104 D．9.2×104‎ ‎【详解】‎ ‎91879≈9.2×104， 故选：D．‎ ‎8．（2018·广西中考模拟）近似数精确到（ ）‎ A．十分位 B．个位 C．十位 D．百位 ‎【解析】‎ 根据近似数的精确度：近似数5.0×102精确到十位．‎ 故选：C．‎ 21‎