决胜2020中考数学压轴题全揭秘下专题16二次函数的存在性问题试题 105页

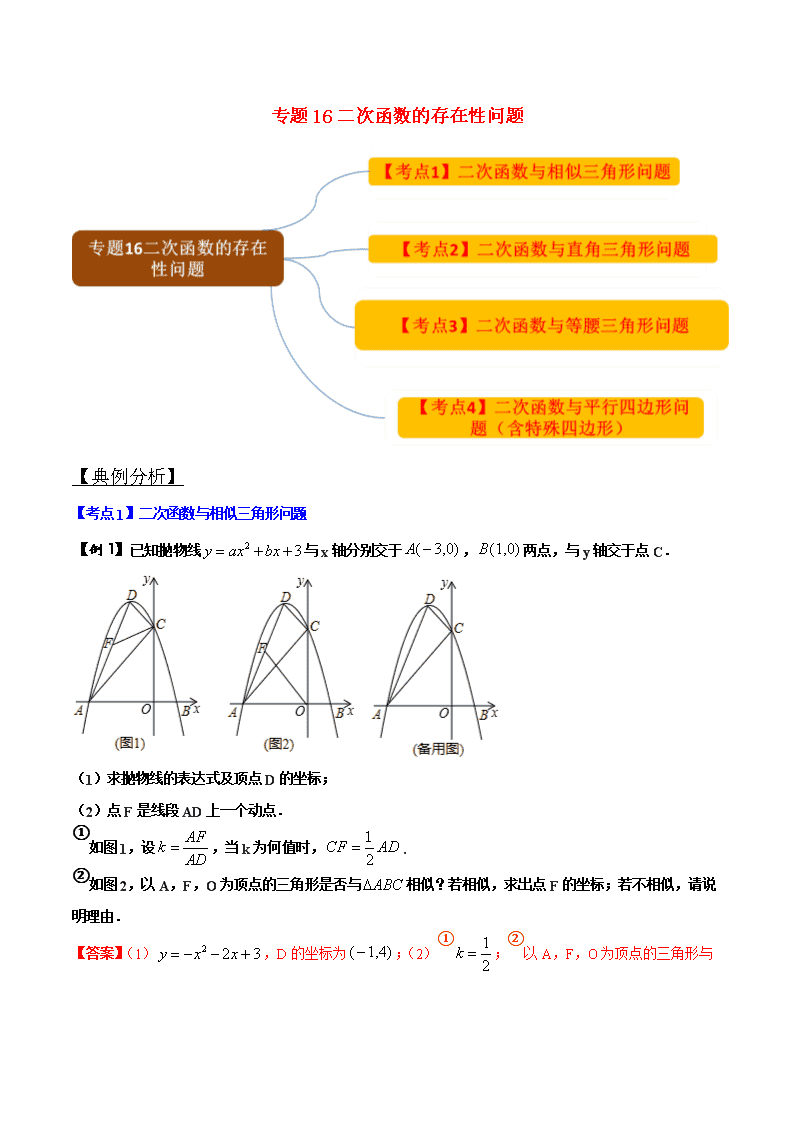
专题 16 二次函数的存在性问题 【典例分析】 【考点 1】二次函数与相似三角形问题 【例 1】已知抛物线 2 3y ax bx   与 x 轴分别交于 ( 3,0)A  ， (1,0)B 两点，与 y 轴交于点 C． （1）求抛物线的表达式及顶点 D 的坐标； （2）点 F 是线段 AD 上一个动点． ①如图 1，设 AFk AD  ，当 k 为何值时， 2CF AD 1 . ②如图 2，以 A，F，O 为顶点的三角形是否与 ABC 相似？若相似，求出点 F 的坐标；若不相似，请说明 理由． 【答案】（1） 2 2 3y x x    ，D 的坐标为 ( 1,4) ；（2）① 1 2k  ；②以 A，F，O 为顶点的三角形与 ABC 相似，F 点的坐标为 6 18,5 5     或 ( 2,2) ． 【解析】(1)将 A、B 两点的坐标代入二次函数解析式，用待定系数法即求出抛物线对应的函数表达式，可 求得顶点 D( 1,4) ； (2)①由 A、C、D 三点的坐标求出 AC 3 2 ， DC 2 ， AD 2 5 ，可得 ΔACD 为直角三角形，若 1CF AD2  ，则点 F 为 AD 的中点，可求出 k 的值； ②由条件可判断 DAC OBC  ，则 OAF ACB  ，若以 A，F，O 为顶点的三角形与 ΔABC 相似， 可分两种情况考虑：当 AOF ABC  或 AOF CAB 45    时，可分别求出点 F 的坐标． 【详解】(1) 抛物线 2y ax bx 3   过点 A( 3,0) ， B(1,0) ， 9 3 3 0 3 0 a b a b       ，解得： 1 2 a b      ， 抛物线解析式为 2y x 2x 3    ；  22y x 2x 3 x 1 4        ， 顶点 D 的坐标为 ( 1,4) ； (2)① 在 RtΔAOC 中， OA 3 ， OC 3 ， 2 2 2AC OA OC 18    ，  D 1,4 ，  C 0,3 ，  A 3,0 ， 2 2 2CD 1 1 2    ， 2 2 2AD 2 4 20    ， 2 2 2AC CD AD   ， ΔACD 为直角三角形，且 ACD 90  ， 1CF AD2  ， F 为 AD 的中点， AF 1 AD 2   ， 1k 2   ； ②在 RtΔACD 中， DC 2 1tan ACD AC 33 2     ， 在 RtΔOBC中， OB 1tan OCB OC 3    ， ACD OCB   ， OA OC ， OAC OCA 45     ， FAO ACB   ， 若以 A，F，O 为顶点的三角形与 ΔABC 相似，则可分两种情况考虑： 当 AOF ABC  时， ΔAOF ΔCBA∽ ， OF BC  ， 设直线 BC 的解析式为 y kx b  ， 0 3 k b b    ，解得： 3 3 k b     ， 直线 BC 的解析式为 y= 3x+3 ， 直线 OF 的解析式为 y= 3x ， 设直线 AD 的解析式为 y=mx+n ， 4 3 0 k b k b      ，解得： 2 6 k b    ， 直线 AD 的解析式为 y=2x 6 ， 2 6 3 y x y x     ，解得： 6 5 18 5 x y      ， 6 18F ,5 5      ． 当 AOF CAB 45    时， ΔAOF ΔCAB∽ ， CAB 45  ， OF AC  ， 直线 OF 的解析式为 y= x ， 2 6 y x y x     ，解得： 2 2 x y     ，  F 2,2  ， 综合以上可得 F 点的坐标为 6 18,5 5     或 ( 2,2) ． 【点睛】本题考查了二次函数的综合题：熟练掌握二次函数图象上点的坐标特征、相似三角形的判定与性 质和直角三角形的性质；会利用待定系数法求函数解析式；理解坐标与图形性质；会运用分类讨论的思想 解决数学问题． 【变式 1-1】如图，抛物线 2y 2ax x c   经过 ( 1,0)A  ， B 两点，且与 y 轴交于点 (0,3)C ，抛物线与 直线 1y x   交于 A ， E 两点． （1）求抛物线的解析式； （2）坐标轴上是否存在一点Q ，使得 AQE 是以 AE 为底边的等腰三角形？若存在，请直接写出点 Q 的 坐标；若不存在，说明理由． （3） P 点在 x 轴上且位于点 B 的左侧，若以 P ， B ，C 为顶点的三角形与 ABE 相似，求点 P 的坐标． 【答案】（1） 2y x 2x 3    ；（2）存在，  4 0Q ， 或 0 4， ，理由见解析；（3） 3p 05      ， 或 9p 02     ， ． 【解析】（1）将 A、C 的坐标代入 2y 2ax x c   求出 a、c 即可得到解析式； （2）先求出 E 点坐标，然后作 AE 的垂直平分线，与 x 轴交于 Q，与 y 轴交于 Q'，根据垂直平分线的性质 可知 Q、与 A、E，Q'与 A、E 组成的三角形是以 AE 为底边的等腰三角形，设 Q 点坐标(0,x)，Q'坐标(0,y)， 根据距离公式建立方程求解即可； （3）根据 A、E 坐标，求出 AE 长度，然后推出∠BAE=∠ABC=45°，设  p 0m， ，由相似得到 PB AB BC AE  或 PB AE BC AB  ，建立方程求解即可． 【详解】（1）将 ( 1,0)A  ， (0,3)C 代入 2y 2ax x c   得： 2 0 3 a c c      ，解得 1 3 a c     ∴抛物线解析式为 2y 2 3   x x （2）存在，理由如下： 联立 y 1x   和 2y x 2x 3    ， 2 y 1 2 3 x y x x         ，解得 1 0 x y     或 4 5 x y     ∴E 点坐标为(4,-5)， 如图，作 AE 的垂直平分线，与 x 轴交于 Q，与 y 轴交于 Q'， 此时 Q 点与 Q'点的坐标即为所求， 设 Q 点坐标(0,x)，Q'坐标(0,y)， 由 QA=QE，Q'A= Q'E 得：      2 21 4 0 5     x x ，        2 2 2 20 1 0 0 4 5      y y 解得 4x  ， 4y  故 Q 点坐标为 4 0， 或  0 4， （3）∵ ( 1,0)A  ，  4 5E ， ∴  2 21 4 5 =5 2   AE ， 当 2 2 3 0x x    时，解得 1x   或 3 ∴B 点坐标为(3,0)， ∴ 3OB OC  ∴ 45ABC   ， 4AB  ， 3 2BC  ， 由直线 1y x   可得 AE 与 y 轴的交点为(0,-1)，而 A 点坐标为(-1,0) ∴∠BAE=45° 设  p 0m， 则 3 mBP   ， ∵ PBC 和 ABE 相似 ∴ PB AB BC AE  或 PB AE BC AB  ，即 3 4 3 2 5 2 m  或 3 5 2 43 2 m  解得 3 5m  或 9 2m   ， ∴ 3p 05      ， 或 9p 02     ， ． 【点睛】本题考查二次函数的综合问题，是中考常见的压轴题型，熟练掌握待定系数法求函数解析式，等 腰三角形的性质，以及相似三角形的性质是解题的关键． 【变式 1-2】如图，已知抛物线 1 ( 2)( )y x x mm     (m＞0)与 x 轴相交于点 A，B，与 y 轴相交于点 C， 且点 A 在点 B 的左侧. （1）若抛物线过点（2，2），求抛物线的解析式； （2）在（1）的条件下，抛物线的对称轴上是否存在一点 H，使 AH+CH 的值最小，若存在，求出点 H 的 坐标；若不存在，请说明理由； （3）在第四象限内，抛物线上是否存在点 M，使得以点 A，B，M 为顶点的三角形与△ACB 相似？若存 在，求出 m 的值；若不存在，请说明理由. 【答案】（1） 21 1 24 2y x x    ；（2）点 H 的坐标为（1， 3 2 ）；（3）当 m= 2 2 2 时，在第四象限内 抛物线上存在点 M，使得以点 A，B，M 为顶点的三角形与△ACB 相似. 【解析】 分析： （1）把点（2，2）代入 1 ( 2)( ) ( 0)y x x m mm      中，解出 m 的值即可得到抛物线的解析式； （2）由（1）中所得解析式求出点 A、B、C 的坐标，由题意可知，点 A、B 关于抛物线的对称轴对称，这 样连接 BC 与对称轴的交点即为所求的点 H，根据 B、C 的坐标求出直线 BC 的解析式即可求得点 H 的坐标； （3）由解析式 1 ( 2)( ) ( 0)y x x m mm      可得点 A、B、C 的坐标分别为（-2，0）、（m，0）和（0，2）， 如下图，由图可知∠ACB 和∠ABM 是钝角，因此存在两种可能性：①当△ACB∽△ABM， ②△ACB∽△MBA，分这两种情况结合题中已知条件进行分析解答即可. 详解： （1）把点（2，2）代入抛物线， 得 2=   1 2 2 2 mm    . 解得 m=4. ∴抛物线的解析式为    21 1 1y x 2 x 4 x x 24 4 2         . （2）令 21 1y x x 2 04 2      ，解得 1 2x 2 x 4  ， . 则 A（-2，0），B（4，0）. 对称轴 x=- 1 2 112 4       . ∵ 21 1y x x 24 2     中当 x=0 时，y=2， ∴点 C 的坐标为（0，2）. ∵点 A 和点 B 关于抛物线的对称轴对称， ∴连接 BC 与对称轴的交点即为点 H，此时 AH+CH 的值最小， 设直线 BC 的解析式为 y=kx+b， 把 B（4，0），C（0，2）代入得： 4 0 2 k b b     ，解得： 1 2 2 k b      ， ∴直线 BC 的解析式为 y= 1 x 22   . ∵当 x=1 时，y= 1 1 22    = 3 2 . ∴点 H 的坐标为（1， 3 2 ）. （3）假设存在点 M，使得以点 A，B，M 为顶点的三角形与△ACB 相似. 如下图，连接 AC，BC，AM，BM，过点 M 作 MN⊥x 轴于点 N， 由图易知，∠ACB 和∠ABM 为钝角， ①当△ACB∽△ABM 时，有 AC AB = AB AM ，即 2AB AC·AM . ∵A（-2，0），C（0，2），即 OA=OC=2， ∴∠CAB=∠BAM= o45 . ∵MN⊥x 轴，∴∠BAM=∠AMN=45°， ∴AN=MN. ∴可设 M 的坐标为：（x，-x-2）（x＞0）， 把点 M 的坐标代入抛物线的解析式，得：-x-2=   1 x 2 x mm    . 化简整理得：x=2m， ∴点 M 的坐标为：（2m，-2m-2）. ∴AM=      2 22m 2 2m 2 2 2 m 1      . ∵ 2AB AC·AM ，AC= 2 2 ，AB=m+2， ∴   2m 2 2 2 2 2 m 1    . 解得：m= 2 2 2 . ∵m＞0， ∴m= 2 2 2 . ②当△ACB∽△MBA 时，有 AB MA = CB BA ，即 2AB CB·MA . ∵∠CBA=∠BAM，∠ANM=∠BOC= o90 ， ∴△ANM∽△BOC，∴ MN AN = CO BO . ∵BO=m，设 ON=x， ∴ 2 MN x = 2 m ，即 MN= 2 m （x+2）. 令 M（x，  2 x 2m   ）（x＞0）， 把 M 点的坐标代入抛物线的解析式， 得  2 x 2m   =   1 x 2 x mm    . 解得 x=m+2.即 M（m+2，  2 m 4m   ）. ∵ 2AB CB·MA ，CB= 2m 4 AN m 4  ， ，MN=  2 m 4m  ， ∴     2 2 22 2 4 m 4m 2 m 4· m 4 m      . 化简整理，得 16=0，显然不成立. 综上所述，当 m= 2 2 2 时，在第四象限内抛物线上存在点 M，使得以点 A，B，M 为顶点的三角形与 △ACB 相似. 点睛：本题是一道二次函数和几何图形综合的题目，解题的要点有以下两点：（1）“知道点 A、B 是关于抛 物线的对称轴对称的，连接 BC 与对称轴的交点即为所求的点 H”是解答第 2 小题的关键；（2）“能根据题意 画出符合要求的图形，知道∠ACB 和∠ABM 为钝角，结合题意得到存在：①当△ACB∽△ABM， ②△ACB∽△MBA 这两种可能情况”是解答第 3 小题的关键. 【考点 2】二次函数与直角三角形问题 【例 2】如图，抛物线  2 0y ax bx c a    的顶点坐标为 2, 1 ，图象与 y 轴交于点  0,3C ，与 x 轴 交于 A 、 B 两点．  1 求抛物线的解析式；  2 设抛物线对称轴与直线 BC 交于点 D ，连接 AC 、 AD ，求 ACD 的面积；  3 点 E 为直线 BC 上的任意一点，过点 E 作 x 轴的垂线与抛物线交于点 F ，问是否存在点 E 使 DEF 为 直角三角形？若存在，求出点 E 坐标，若不存在，请说明理由． 【答案】(1) 2 2  ( 2) 1 4 3y x x x      ;(2)2;(3)见解析. 【解析】（1）可设抛物线解析式为顶点式，把 C 点坐标代入可求得抛物线解析式； （2）由抛物线解析式可求得 A、B 坐标，利用待定系数法可求得直线 BC 解析式，利用对称轴可求得 D 点 坐标，则可求得 AD2、AC2 和 CD2，利用勾股定理的逆定理可判定△ACD 为直角三角形，则可求得其面积； （3）根据题意可分∠DFE=90°和∠EDF=90°两种情况，当∠DFE=90°时，可知 DF∥x 轴，则可求得 E 点纵 坐标，代入抛物线解析式可求得 E 点坐标；当∠EDF=90°时，可求得直线 AD 解析式，联立直线 AC 和抛物 线解析式可求得点 E 的横坐标，代入直线 BC 可求得点 E 的坐标． 【详解】解：  1 ∵抛物线的顶点坐标为 2, 1 ， ∴可设抛物线解析式为  2( 2) 1 0y a x a    ， 把  0,3C 代入可得 2(0 2) 1 3a    ，解得 1a  ， ∴抛物线解析式为 2 2( 2) 1 4 3y x x x      ；  2 在 2 4 3y x x   中，令 0y  可得 2 4 3 0x x   ，解得 1x  或 3x  ， ∴  1,0A ，  3,0B ， 设直线 BC 解析式为 3y kx  ，把  3,0B 代入得：3 3 0k   ，解得 1k   ， ∴直线 BC 解析式为 3y x   ， 由 1 可知抛物线的对称轴为 2x  ，此时 2 3 1y     ， ∴  2,1D ， ∴ 2 2AD  ， 2 10AC  ， 2 8CD  ， ∵ 2 2 2AD CD AC  ， ∴ ACD 是以 AC 为斜边的直角三角形， ∴ 1 1 2 2 2 22 2ACDS AD CD      ；  3 由题意知 / /EF y 轴，则 90FED OCB     ， ∴ DEF 为直角三角形，分 90DFE   和 90EDF   两种情况， ①当 90DFE   时，即 / /DF x 轴，则 D 、 F 的纵坐标相同， ∴ F 点纵坐标为1， ∵点 F 在抛物线上， ∴ 2 4 3 1x x   ，解得 2 2x   ，即点 E 的横坐标为 2 2 ， ∵点 E 在直线 BC 上， ∴当 2 2x   时， 3 1 2y x     ，当 2 2x   时， 3 1 2y x     ， ∴ E 点坐标为 2 2,1 2  或 2 2,1 2  ； ②当 90EDF   时， ∵  1,0A ，  2,1D ， ∴直线 AD 解析式为 1y x  ， ∵直线 BC 解析式为 3y x   ， ∴ AD BC ， ∴直线 AD 与抛物线的交点即为 E 点， 联立直线 AD 与抛物线解析式有 2 4 3 1x x x    ，解得 1x  或 4x  ， 当 1x  时， 3 2y x    ，当 4x  时， 3 1y x     ， ∴ E 点坐标为 1,2 或 4, 1 ， 综上可知存在满足条件的点 E ，其坐标为 2 2,1 2  或 2 2,1 2  或 1,2 或 4, 1 ． 【点睛】考查了待定系数法求函数解析式，利用已知的顶点坐标，列出方程组，可以求出函数解析式. 【变式 2-1】如图，经过 x 轴上 ( 1 0) (3 0)A B ，， ， 两点的抛物线 2( 1) 4y m x m   （ 0m  ）交 y 轴于点 C ，设抛物线的顶点为 D ，若以 DB 为直径的⊙G 经过点C ，求解下列问题： （1）用含 m 的代数式表示出C D， 的坐标； （2）求抛物线的解析式； （3）能否在抛物线上找到一点 Q，使 BDQ△ 为直角三角形？如能，求出Q 点的坐标，若不能，请说明理 由。 【答案】（1）点C 的坐标为 (0 3 )C m， ,点 D 的坐标为 (1 4 )m， ；（2） 抛物线的解析式为 2y x 2x 3    ； （3）满足题意的Q 点有三个： (0 3)， 、 3 9 2 4     ， 和 1 15 2 4      ， 【解析】 【试题分析】 （1）  21 4y m x m   是顶点式，则顶点 D 的坐标为  0 3C m， ,当 x=0,则 y=-3m,即点C 的坐标为  0 3C m， ； （2）连接 CD 、 BC，过点 D 作 DE y 轴于 E ，如图①所示:根据直径所对的圆周角是直角，得 90DCB   ,出现“一线三等角模型”，得 DEC COB ∽ 根据相似三角形的性质 得： DE EC CO OB  1 3 3 m m  即 ，解得 1m   ，则抛物线的解析式为 2 2 3y x x    . （3）分三种情况分类讨论： 90BQD   （图①）显然Q 与C 点重合，点Q 坐标为  0 3Q ， ； DBQ =90 （图②）作QF y 轴于 F ，DH x 轴于 H ，根据两角对应相等，两三角形相似，得 Rt RtDHB BFQ ∽ ， DH HB BF FQ  ，则 • •DH FQ BF HB ，由于点Q 坐标 2 2 3k k k  ， ，则    24 2 3 2 3k k k    ， 解得： 3  2k   由 3 2k   得Q 坐标： 3 9 2 4Q     ， ； BDQ =90（图③）延长 DQ 交 y 轴于 M ，作 DE y 轴于 E ， DH x 轴于 H ,同理可证： DEM DHB ∽ ，则 DE EM DH HB  ，即 1 4 2 EM ,得 1 2EM  ，点 M 的坐标 为 70 2      ， ，设 DM 所在的直线解析式为 y=kx+b,用待定系数法，把 M 70 2      ， 和 D（1,4）代入得： 7 2 4 b k b      解得： 1 7,2 2k b  则直线 DM 的解析式为 1 7 2 2y x  ,把 1 7 2 2y x  代入 2 2 3y x x    得： 22 3 1 0x x   ，解得， 1 2x  ，最后把 1 2x  代入 1 7 2 2y x  得 15 4y  ,点Q 的坐标为 1 15 2 4      ， 综上述，Q点有三个： 0 3， 、 3 9 2 4     ， 和 1 15 2 4      ， 【试题解析】 （1）∵y  21 4m x m   是顶点式 ∴点 D 的坐标为 1 4m， 当 x=0 时，y= -3m 点C 的坐标为  0 3C m， （2） 连接 CD 、 BC，过点 D 作 DE y 轴于 E ，如图①所示： ∵BD 是⊙G 的直径 ∴∠DCB= 090 ∴∠ECD+∠BCO= 090 ∵∠ECD+∠EDC= 090 ∴∠BCO=∠EDC ∵∠DEC=∠BOC= 090 ∴ DEC COB ∽ DE EC CO OB   1 3 3 m m   2 1m  1m   ∵ 0m  ∴ 1m   ∴抛物线的解析式为 2 2 3y x x    （3）能在抛物线上找到一点 Q，使△BDQ 为直角三角形 很明显，点C 即在抛物线上，又在⊙G 上， 90BCD  ，这时Q 与C 点重合 点Q 坐标为  0 3Q ， 如图②，若 DBQ 为90 ，作QF y 轴于 F ， DH x 轴于 H 同理可证： Rt RtDHB BFQ ∽ ∴ DH HB BF FQ  ∴ • •DH FQ BF HB ∵点Q坐标 2 2 3k k k  ， ∴    24 2 3 2 3k k k    化简得： 22 3 9 0k k   ,解得： 3k  （不合题意，舍去）， 3 2k   由 3 2k   得Q 坐标： 3 9 2 4Q     ， 若 BDQ 为90 ,如图③，延长 DQ 交 y 轴于 M ， 作 DE y 轴于 E ， DH x 轴于 H ,同理可证： DEM DHB ∽ ∴ DE EM DH HB  则 1 4 2 EM ,得 1 2EM  ，点 M 的坐标为 70 2      ， 设 DM 所在的直线解析式为 y=kx+b,把 M 70 2      ， 和 D（1,4）代入得： 7 2 4 b k b      解得： 1 7,2 2k b  ∴直线 DM 的解析式为 1 7 2 2y x  ,把 1 7 2 2y x  代入 2 2 3y x x    得： 22 3 1 0x x   解为： 1x  （不合题意，舍去）， 1 2x  ， 把 1 2x  代入 1 7 2 2y x  得 15 4y  ,点Q 的坐标为 1 15 2 4      ， 综合上述，满足题意的Q点有三个： 0 3， 、 3 9 2 4     ， 和 1 15 2 4      ， 【方法点睛】本题目是一道二次函数的综合题，涉及到顶点坐标，与坐标轴的交点，一线三等角证相似， 并且多次运用相似三角形的对应边成比例，直角三角形的确定（3 种情况分类讨论），难度较大. 【变式 2-2】已知抛物线 2 2 1y x x m    与 x 轴只有一个交点，且与 y 轴交于 A 点，如图，设它的顶 点为 B． （1）求 m 的值； （2）过 A 作 x 轴的平行线，交抛物线于点 C，求证：△ABC 是等腰直角三角形； （3）将此抛物线向下平移 4 个单位后，得到抛物线 y，且与 x 轴的左半轴交于 E 点，与 y 轴交于 F 点， 如图．请在抛物线 y上求点 P，使得△ EFP 是以 EF 为直角边的直角三角形？ 【答案】（1）m = 2；（2）证明见解析；（3）满足条件的 P 点的坐标为（ 10 3 ，13 9 ）或（ 7 3 ， 20 9  ）． 【解析】 试题分析：（1）根据抛物线与 x 轴只有一个交点可知△的值为 0，由此得到一个关于 m 的一元一次方程， 解此方程可得 m 的值； （2）根据抛物线的解析式求出顶点坐标，根据 A 点在 y 轴上求出 A 点坐标，再求 C 点坐标，根据三个点 的坐标得出△ABC 为等腰直角三角形； （3）根据抛物线解析式求出 E、F 的坐标，然后分别讨论以 E 为直角顶点和以 F 为直角顶点 P 的坐标． 试题解析：（1）∵抛物线 y=x2-2x+m-1 与 x 轴只有一个交点， ∴△=（-2）2-4×1×（m-1）=0， 解得，m=2； （2）由（1）知抛物线的解析式为 y=x2-2x+1=（x-1）2，易得顶点 B（1，0）， 当 x=0 时，y=1，得 A（0，1）． 由 1=x2-2x+1，解得，x=0（舍）或 x=2，所以 C 点坐标为：（2，1）． 过 C 作 x 轴的垂线，垂足为 D，则 CD=1，BD=xD-xB=1． ∴在 Rt△CDB 中，∠CBD=45°，BC= 2 ． 同理，在 Rt△AOB 中，AO=OB=1，于是∠ABO=45°，AB= 2 ． ∴∠ABC=180°-∠CBD-∠ABO=90°，AB=BC， 因此△ABC 是等腰直角三角形； （3）由题知，抛物线 C′的解析式为 y=x2-2x-3， 当 x=0 时，y=-3； 当 y=0 时，x=-1 或 x=3， ∴E（-1，0），F（0，-3），即 OE=1，OF=3． 第一种情况：若以 E 点为直角顶点，设此时满足条件的点为 P1（x1，y1），作 P1M⊥x 轴于 M． ∵∠P1EM+∠OEF=∠EFO+∠OEF=90°， ∴∠P1EM=∠EFO，得 Rt△EFO∽Rt△P1EM， 则 1 1 3 PM OE EM OF ＝ ＝ ，即 EM=3P1M． ∵EM=x1+1，P1M=y1， ∴x1+1=3y1① 由于 P1（x1，y1）在抛物线 C′上， 则有 3（x12-2x1-3）=x1+1， 整理得，3x12-7x1-10=0，解得， x1＝10 3 ，或 x2=-1（舍去） 把 x1＝ 10 3 代入①中可解得， y1=13 9 ． ∴P1（10 3 ，13 9 ）． 第二种情况：若以 F 点为直角顶点，设此时满足条件的点为 P2（x2，y2），作 P2N⊥y 轴于 N． 同第一种情况，易知 Rt△EFO∽Rt△FP2N， 得 2 1 3 FN OE P N OF ＝ ＝ ，即 P2N=3FN． ∵P2N=x2，FN=3+y2， ∴x2=3（3+y2）② 由于 P2（x2，y2）在抛物线 C′上， 则有 x2=3（3+x22-2x2-3）， 整理得 3x22-7x2=0，解得 x2=0（舍）或 x2＝ 7 3 ． 把 x2＝ 10 3 代入②中可解得， y2＝− 20 9 ． ∴P2（ 7 3 ，− 20 9 ）． 综上所述，满足条件的 P 点的坐标为：（ 10 3 ，13 9 ）或（ 7 3 ，− 20 9 ）. 【考点 3】二次函数与等腰三角形问题 【例 3】如图，已知：二次函数 y＝x2+bx+c 的图象与 x 轴交于 A，B 两点，其中 A 点坐标为（﹣3，0）， 与 y 轴交于点 C，点 D（﹣2，﹣3）在抛物线上． （1）求抛物线的表达式； （2）抛物线的对称轴上有一动点 P，求出 PA+PD 的最小值； （3）若抛物线上有一动点 M，使△ABM 的面积等于△ABC 的面积，求 M 点坐标． （4）抛物线的对称轴上是否存在动点 Q，使得△BCQ 为等腰三角形？若存在，求出点 Q 的坐标；若不存 在，说明理由． 【答案】（1）y＝x2+2x﹣3；（2）3 2 ；（3）点 M 的坐标为（﹣1﹣ 7 ，3），（﹣1+ 7 ，3），（﹣2，﹣3）； （4）存在；点 Q 的坐标为（﹣1， 6 ），（﹣1，﹣ 6 ），（﹣1，0），（﹣1，﹣6），（﹣1，﹣1）． 【解析】（1）由点 A，D 的坐标，利用待定系数法即可求出抛物线的表达式； （2）利用二次函数图象上点的坐标特征可求出点 B 的坐标，连接 BD，交抛物线的对称轴于点 P，由抛物 线的对称性及两点之间线段最短可得出此时 PA+PD 取最小值，最小值为线段 BD 的长度，再由点 B，D 的 坐标，利用两点间的距离公式可求出 PA+PD 的最小值； （3）利用二次函数图象上点的坐标特征可求出点 C 的坐标，设点 M 的坐标为（x，x2+2x-3），由△ABM 的 面积等于△ABC 的面积可得出关于 x 的一元二次方程，解之即可求出点 M 的坐标； （4）设点 Q 的坐标为（-1，m），结合点 B，C 的坐标可得出 CQ2，BQ2，BC2，分 BQ=BC，CQ=CB 及 QB=QC 三种情况，找出关于 m 的一元二次（或一元一次）方程，解之即可得出点 Q 的坐标． 【详解】解：（1）将 A（﹣3，0），D（﹣2，﹣3）代入 y＝x2+bx+c，得： 9 3 0 4 2 3 b c b c       ＝ ＝ ，解得： 2 3 b c     ， ∴抛物线的表达式为 y＝x2+2x﹣3． （2）当 y＝0 时，x2+2x﹣3＝0， 解得：x1＝﹣3，x2＝1， ∴点 B 的坐标为（1，0）． 连接 BD，交抛物线的对称轴于点 P，如图 1 所示． ∵PA＝PB， ∴此时 PA+PD 取最小值，最小值为线段 BD 的长度． ∵点 B 的坐标为（1，0），点 D 的坐标为（﹣2，﹣3）， ∴BD＝ 2 2( 2 1) ( 3 0)     ＝3 2 ， ∴PA+PD 的最小值为 3 2 ． （3）当 x＝0 时，y＝x2+2x﹣3＝﹣3， ∴点 C 的坐标为（0，﹣3）． 设点 M 的坐标为（x，x2+2x﹣3）． ∵S△ABM＝S△ABC， ∴|x2+2x﹣3|＝3，即 x2+2x﹣6＝0 或 x2+2x＝0， 解得：x1＝﹣1﹣ 7 ，x2＝﹣1+ 7 ，x3＝﹣2，x4＝0（舍去）， ∴点 M 的坐标为（﹣1﹣ 7 ，3），（﹣1+ 7 ，3），（﹣2，﹣3）． （4）设点 Q 的坐标为（﹣1，m）． ∵点 B 的坐标为（1，0），点 C 的坐标为（0，﹣3）， ∴CQ2＝（﹣1﹣0）2+[m﹣（﹣3）]2＝m2+6m+10，BQ2＝（﹣1﹣1）2+（m﹣0）2＝m2+4，BC2＝（0﹣1） 2+（﹣3﹣0）2＝10． 分三种情况考虑（如图 2 所示）： ①当 BQ＝BC 时，m2+4＝10， 解得：m1＝ 6 ，m2＝﹣ 6 ， ∴点 Q1 的坐标为（﹣1， 6 ），点 Q2 的坐标为（﹣1，﹣ 6 ）； ②当 CQ＝CB 时，m2+6m+10＝10， 解得：m3＝0，m4＝﹣6， ∴点 Q3 的坐标为（﹣1，0），点 Q4 的坐标为（﹣1，﹣6）； ③当 QB＝QC 时，m2+4＝m2+6m+10， 解得：m5＝﹣1， ∴点 Q5 的坐标为（﹣1，﹣1）． 综上所述：抛物线的对称轴上存在动点 Q，使得△BCQ 为等腰三角形，点 Q 的坐标为（﹣1， 6 ），（﹣1， ﹣ 6 ），（﹣1，0），（﹣1，﹣6），（﹣1，﹣1）． 【点睛】本题考查了待定系数法求二次函数解析式、二次函数图象上点的坐标特征、二次函数的性质、两 点间的距离公式、三角形的面积、等腰三角形的性质以及解一元二次（或一元一次）方程，解题的关键是： （1）由点的坐标，利用待定系数法求出二次函数表达式；（2）利用两点之间线段最短，找出点 P 的位置； （3）利用两三角形面积相等，找出关于 x 的一元二次方程；（4）分 BQ=BC，CQ=CB 及 QB=QC 三种情况， 找出关于 m 的方程． 【变式 3-1】如图，抛物线 32  bxaxy 与 x 轴交于点 A（1，0）和 B（3，0）． （1）求抛物线的解析式； （2）若抛物线的对称轴交 x 轴于点 E，点 F 是位于 x 轴上方对称轴上一点，FC∥x 轴，与对称轴右侧的抛 物线交于点 C，且四边形 OECF 是平行四边形，求点 C 的坐标； （3）在（2）的条件下，抛物线的对称轴上是否存在点 P，使△OCP 是等腰三角形？若存在，请直接写出 点 P 的坐标；若不存在，请说明理由． 【答案】（1） 342  xxy ；（2）C（4，3）；（3）P（ 2   21， ）或（ 2   21， ）或（ 2  3+ 21， ）或（ 2  3 21， ）． 【解析】 试题分析：（1）把点 A、B 的坐标代入函数解析式，解方程组求出 a、b 的值，即可得解； （2）根据抛物线解析式求出对称轴，再根据平行四边形的对角线互相平分求出点 C 的横坐标，然后代入函 数解析式计算求出纵坐标，即可得解； （3）设 AC、EF 的交点为 D，根据点 C 的坐标写出点 D 的坐标，然后分①O 是顶角，②C 是顶角，③P 是 顶角三种情况讨论． 试题解析：（1）把点 A（1，0）和 B（3，0）代入 32  bxaxy 得，      0339 03 ba ba ，解得      4 1 b a ，所以，抛物线的解析式为 342  xxy ； （2）抛物线的对称轴为直线 x=2， ∵四边形 OECF 是平行四边形∴点 C 的横坐标是 4， ∵点 C 在抛物线上，∴ 334442 y ， ∴点 C 的坐标为（4，3）； （3）∵点 C 的坐标为（4，3），∴OC 的长为 5， ①点 O 是顶角顶点时，OP=OC=5， ∵ 222 EPOEOP  ，OE=2∴ 2125 22 EP ， 所以，点 P 的坐标为（2， 21 ）或（2，- 21 ）； ②点 C 是顶角顶点时，CP=OC=5，同理求出 PF= 21 ，所以，PE= 21 3 ， 所以，点 P 的坐标为（2， 3 21 ）或（2， 3 21 ）； ③点 P 是顶角顶点时，点 P 在 OC 上，不存在. 综上所述，抛物线的对称轴上存在点 P（2， 21 ）或（2，- 21 ）或（2，3 21 ）或（2， 3 21 ）， 使△OCP 是等腰三角形． 考点：二次函数综合题． 【变式 3-2】如图，抛物线 与直线 相交于 两点，且抛 物线经过点 . （1）求抛物线的解析式； （2）点 是抛物线上的一个动点（不与点 、点 重合），过点 作直线 轴于点 ，交直线 于点 . ①当 时，求 点坐标； ② 是否存在点 使 为等腰三角形，若存在请直接写出点 的坐标，若不存在，请说明理由. 【答案】（1）y=﹣x2+4x+5；（2）①P 点坐标为（2，9）或（6，﹣7）；②（ ， ）或（4+ ，﹣4 ﹣8）或（4﹣ ，4 ﹣8）或（0，5）． 【解析】 试题分析：（1）由直线解析式可求得 B 点坐标，由 A、B、C 三点的坐标，利用待定系数法可求得抛物线解 析式； （2）①可设出 P 点坐标，则可表示出 E、D 的坐标，从而可表示出 PE 和 ED 的长，由条件可知到关于 P 点坐标的方程，则可求得 P 点坐标； ②由 E、B、C 三点坐标可表示出 BE、CE 和 BC 的长，由等腰三角形的性质可得到关于 E 点坐标的方程， 可求得 E 点坐标，则可求得 P 点坐标． 试题解析：（1）∵点 B（4，m）在直线 y=x+1 上， ∴m=4+1=5， ∴B（4，5）， 把 A、B、C 三点坐标代入抛物线解析式可得 ，解得 ， ∴抛物线解析式为 y=﹣x2+4x+5； （2）①设 P（x，﹣x2+4x+5），则 E（x，x+1），D（x，0）， 则 PE=|﹣x2+4x+5﹣（x+1）|=|﹣x2+3x+4|，DE=|x+1|， ∵PE=2ED， ∴|﹣x2+3x+4|=2|x+1|， 当﹣x2+3x+4=2（x+1）时，解得 x=﹣1 或 x=2，但当 x=﹣1 时，P 与 A 重合不合题意，舍去， ∴P（2，9）； 当﹣x2+3x+4=﹣2（x+1）时，解得 x=﹣1 或 x=6，但当 x=﹣1 时，P 与 A 重合不合题意，舍去， ∴P（6，﹣7）； 综上可知 P 点坐标为（2，9）或（6，﹣7）； ②设 P（x，﹣x2+4x+5），则 E（x，x+1），且 B（4，5），C（5，0）， ∴BE= |x﹣4|，CE= ， BC= ， 当△BEC 为等腰三角形时，则有 BE=CE、BE=BC 或 CE=BC 三种情况， 当 BE=CE 时，则 |x﹣4|= ，解得 x= ，此时 P 点坐标为（ ， ）； 当 BE=BC 时，则 |x﹣4|= ，解得 x=4+ 或 x=4﹣ ，此时 P 点坐标为（4+ ，﹣4 ﹣8） 或（4﹣ ，4 ﹣8）； 当 CE=BC 时，则 = ，解得 x=0 或 x=4，当 x=4 时 E 点与 B 点重合，不合题意，舍 去，此时 P 点坐标为（0，5）； 综上可知存在满足条件的点 P，其坐标为（ ， ）或（4+ ，﹣4 ﹣8）或（4﹣ ，4 ﹣ 8）或（0，5）． 考点：二次函数综合题． 【考点 4】二次函数与平行四边形问题 【例 4】如图，抛物线 y=ax2+bx+c 与 x 轴相交于点 A（﹣3，0），B（1，0），与 y 轴相交于（0，﹣ 3 2 ）， 顶点为 P． （1）求抛物线解析式； （2）在抛物线是否存在点 E，使△ABP 的面积等于△ABE 的面积？若存在，求出符合条件的点 E 的坐标； 若不存在，请说明理由； （3）坐标平面内是否存在点 F，使得以 A、B、P、F 为顶点的四边形为平行四边形？直接写出所有符合条 件的点 F 的坐标，并求出平行四边形的面积． 【答案】（1）y= 1 2 x2+x﹣ 3 2 （2）存在，（﹣1﹣2 2 ，2）或（﹣1+2 2 ，2）（3）点 F 的坐标为（﹣1，2）、 （3，﹣2）、（﹣5，﹣2），且平行四边形的面积为 8 【解析】（1）设抛物线解析式为 y=ax2+bx+c，把（﹣3，0），（1，0），（0， 3 2 ）代入求出 a、b、c 的值即可； （2）根据抛物线解析式可知顶点 P 的坐标，由两个三角形的底相同可得要使两个三角形面积相等则高相等， 根据 P 点坐标可知 E 点纵坐标，代入解析式求出 x 的值即可；（3）分别讨论 AB 为边、AB 为对角线两种情 况求出 F 点坐标并求出面积即可； 【详解】（1）设抛物线解析式为 y=ax2+bx+c，将（﹣3，0），（1，0），（0，3 2 ）代入抛物线解析式得 0 9a-3b+c 0 a+b+c 3 2c          ， 解得：a= 1 2 ，b=1，c=﹣ 3 2 ∴抛物线解析式：y= 1 2 x2+x﹣ 3 2 （2）存在． ∵y= 1 2 x2+x﹣ 3 2 = 1 2 （x+1）2﹣2 ∴P 点坐标为（﹣1，﹣2） ∵△ABP 的面积等于△ABE 的面积， ∴点 E 到 AB 的距离等于 2， 设 E（a，2）， ∴ 1 2 a2+a﹣ 3 2 =2 解得 a1=﹣1﹣2 2 ，a2=﹣1+2 2 ∴符合条件的点 E 的坐标为（﹣1﹣2 2 ，2）或（﹣1+2 2 ，2） （3）∵点 A（﹣3，0），点 B（1，0）， ∴AB =4 若 AB 为边，且以 A、B、P、F 为顶点的四边形为平行四边形 ∴AB∥PF，AB=PF=4 ∵点 P 坐标（﹣1，﹣2） ∴点 F 坐标为（3，﹣2），（﹣5，﹣2） ∴平行四边形的面积=4×2=8 若 AB 为对角线，以 A、B、P、F 为顶点的四边形为平行四边形 ∴AB 与 PF 互相平分 设点 F（x，y）且点 A（﹣3，0），点 B（1，0），点 P（﹣1，﹣2） ∴ 3 1 1 2 2 0 0 2 2 2 x y          ， ∴x=﹣1，y=2 ∴点 F（﹣1，2） ∴平行四边形的面积= 1 2 ×4×4=8 综上所述：点 F 的坐标为（﹣1，2）、（3，﹣2）、（﹣5，﹣2），且平行四边形的面积为 8． 【点睛】本题考查待定系数法求二次函数解析式及二次函数的几何应用，分类讨论并熟练掌握数形结合的 数学思想方法是解题关键. 【变式 4-1】如图，在平面直角坐标系中，抛物线 ，经过 A（0，﹣4），B（ ，0），C （ ，0）三点，且 ． （1）求 b，c 的值； （2）在抛物线上求一点 D，使得四边形 BDCE 是以 BC 为对角线的菱形； （3）在抛物线上是否存在一点 P，使得四边形 BPOH 是以 OB 为对角线的菱形？若存在，求出点 P 的坐标， 并判断这个菱形是否为正方形？若不存在，请说明理由． 【答案】（1） ， ；（2）D（ ， ）；（3）存在一点 P（﹣3，4），使得四边形 BPOH 为菱形， 不能为正方形． 【解析】 试题分析：（1）把 A（0，﹣4）代入可求 c，运用根与系数的关系及 ，可求出 b； （2）因为菱形的对角线互相垂直平分，故菱形的另外一条对角线必在抛物线的对称轴上，满足条件的 D 点， 就是抛物线的顶点； （3）由四边形 BPOH 是以 OB 为对角线的菱形，可得 PH 垂直平分 OB，求出 OB 的中点坐标，代入抛物线 解析式即可，再根据所求点的坐标与线段 OB 的长度关系，判断是否为正方形即可． 试题解析：（1）∵抛物线 ，经过点 A（0，﹣4），∴c=﹣4， 又∵由题意可知， 、 是方程 的两个根，∴ ， ，由已知得 ，∴ ，∴ ，∴ ，解得： ， 当 b= 时，抛物线与 x 轴的交点在 x 轴的正半轴上，不合题意，舍去．∴b= ； （2）∵四边形 BDCE 是以 BC 为对角线的菱形，根据菱形的性质，点 D 必在抛物线的对称轴上，又 ∵ = ，∴抛物线的顶点（ ， ）即为所求的点 D； （3）∵四边形 BPOH 是以 OB 为对角线的菱形，点 B 的坐标为（﹣6，0），根据菱形的性质，点 P 必是直 线 x=﹣3 与抛物线 的交点，∴当 x=﹣3 时， =4，∴在 抛物线上存在一点 P（﹣3，4），使得四边形 BPOH 为菱形． 四边形 BPOH 不能成为正方形，因为如果四边形 BPOH 为正方形，点 P 的坐标只能是（﹣3，3），但这一点 不在抛物线上． 考点：1．二次函数综合题；2．探究型；3．存在型；4．压轴题． 【变式 4-2】如图，抛物线 与直线 交于 ， 两点，直线 交 轴与点 ，点 是直线 上的动点，过点 作 轴交 于点 ，交抛物线于点 . (1)求抛物线 的表达式； (2)连接 ， ，当四边形 是平行四边形时，求点 的坐标； (3)①在 轴上存在一点 ，连接 ， ，当点 运动到什么位置时，以 为顶点的四边形是矩 形？求出此时点 的坐标； ②在①的前提下，以点 为圆心， 长为半径作圆，点 为 上一动点，求 的最小值. 【答案】(1) y=﹣x2﹣2x+4；(2) G（﹣2，4）；(3)①E（﹣2，0）．H（0，﹣1）；② 5 5 2 ． 【解析】 试题分析:（1）利用待定系数法求出抛物线解析式； （2）先利用待定系数法求出直线 AB 的解析式，进而利用平行四边形的对边相等建立方程求解即可； （3）①先判断出要以点 A，E，F，H 为顶点的四边形是矩形，只有 EF 为对角线，利用中点坐标公式建立 方程即可； ②先取 EG 的中点 P 进而判断出△PEM∽△MEA 即可得出 PM= AM，连接 CP 交圆 E 于 M，再求出点 P 的坐标即可得出结论． 试题解析：（1）∵点 A（﹣4，﹣4），B（0，4）在抛物线 y=﹣x2+bx+c 上， ∴ 16 4 4 4 b c c        ， ∴ 2 4 b c     ， ∴抛物线的解析式为 y=﹣x2﹣2x+4； （2）设直线 AB 的解析式为 y=kx+n 过点 A，B， ∴ ， ∴ ， ∴直线 AB 的解析式为 y=2x+4， 设 E（m，2m+4）， ∴G（m，﹣m2﹣2m+4）， ∵四边形 GEOB 是平行四边形， ∴EG=OB=4， ∴﹣m2﹣2m+4﹣2m﹣4=4， ∴m=﹣2， ∴G（﹣2，4）； （3）①如图 1， 由（2）知，直线 AB 的解析式为 y=2x+4， ∴设 E（a，2a+4）， ∵直线 AC：y=﹣ x﹣6， ∴F（a，﹣ a﹣6）， 设 H（0，p）， ∵以点 A，E，F，H 为顶点的四边形是矩形， ∵直线 AB 的解析式为 y=2x+4，直线 AC：y=﹣ x﹣6， ∴AB⊥AC， ∴EF 为对角线， ∴ （﹣4+0）= （a+a）， （﹣4+p）= （2a+4﹣ a﹣6）， ∴a=﹣2，P=﹣1， ∴E（﹣2，0）．H（0，﹣1）； ②如图 2， 由①知，E（﹣2，0），H（0，﹣1），A（﹣4，﹣4）， ∴EH= ，AE=2 ， 设 AE 交⊙E 于 G，取 EG 的中点 P， ∴PE= ， 连接 PC 交⊙E 于 M，连接 EM， ∴EM=EH= ， ∴ = ， ∵ = ， ∴ ， ∵∠PEM=∠MEA， ∴△PEM∽△MEA， ∴ ， ∴PM= AM， ∴ AM+CM 的最小值=PC， 设点 P（p，2p+4）， ∵E（﹣2，0）， ∴PE2=（p+2）2+（2p+4）2=5（p+2）2， ∵PE= ， ∴5（p+2）2= ， ∴p=﹣ 或 p=﹣ （由于 E（﹣2，0），所以舍去）， ∴P（﹣ ，﹣1）， ∵C（0，﹣6）， ∴PC= ， 即： AM+CM= ． 考点：二次函数综合题． 【达标训练】 一、单选题 1．将抛物线 y=﹣2x2﹣1 向上平移若干个单位，使抛物线与坐标轴有三个交点，如果这些交点能构成直角 三角形，那么平移的距离为（ ） A． 3 2 个单位 B．1 个单位 C． 1 2 个单位 D． 2 个单位 【答案】A 【解析】 试题分析设抛物线向上平移 a（a＞1）个单位，使抛物线与坐标轴有三个交点， 且这些交点能构成直角三角形， 则有平移后抛物线的解析式为：y=﹣2x2﹣1+a，AM=a， ∵抛物线 y=﹣2x2﹣1 与 y 轴的交点 M 为（0，﹣1），即 OM=1， ∴OA=AM﹣OM=a﹣1， 令 y=﹣2x2﹣1+a 中 y=0，得到﹣2x2﹣1+a=0， 解得：x=± 1 2 a  ，∴B（﹣ 1 2 a  ，0），C（ 1 2 a  ，0），即 BC=2 1 2 a  ， 又△ABC 为直角三角形，且 B 和 C 关于 y 轴对称，即 O 为 BC 的中点， ∴AO= 1 2 BC，即 a﹣1= 1 2 a  ，两边平方得：（a﹣1）2= ， ∵a﹣1≠0，∴a﹣1= 1 2 ，解得：a= 3 2 ． 故选 A 【考点】二次函数图象与几何变换． 2．如图，抛物线 2y x 2x 3    与 y 轴交于点C ，点 (0,1)D ，点 P 是抛物线上的动点，若 PCD 是以 CD 为底的等腰三角形，则 tan CDP 的值为（ ）． A．1 2 2 + 或 1 2 2  B． 2 1 或 2 1 C． 2 1 2  或 2 1 2  D．1 2 或1 2 【答案】B 【解析】 作CD 中垂线交抛物线于 1P ， 2P （ 1P 在 2P 左侧），交 y 轴于点 E ;连接 P1D,P2D. 易得 (0,3)C (0,1)D (0,2)E ． ∴ 1 2 2P Py y  ， 1DE  ． 将 2y  代入 2y x 2x 3    中得 1 1 2x   ， 2 1 2x   ． ∴ 1 2 1PE   ， 2 2 1P E   ． ∴ 1 1tan 2 1PECDP ED   ∠ ， 2 2tan 2 1P ECDP ED   ∠ ． 故选 B. 当△PCD 是以 CD 为底的等腰三角形时,则 P 点在线段 CD 的垂直平分线上,由 C、D 坐标可求得线段 CD 中 点的坐标,从而可以知道 P 点的纵坐标,代入抛物线解析式可求得 P 点坐标. 二、填空题 3．如图，抛物线 2 1y x  的顶点为C ，直线 1y x  与抛物线交于 A ， B 两点． M 是抛物线上一点， 过 M 作 MG x 轴，垂足为G ．如果以 A ， M ，G 为顶点的三角形与 ABC 相似，那么点 M 的坐标是 ________． 【答案】 4,15 ，  2,3 ， 4 7,3 9      ． 【解析】根据抛物线的解析式，易求得 A（-1，0），D（1，0），C（0，-1）；则△ACD 是等腰直角三角形， 由于 AP∥DC，可知∠BAC=90°；根据 D、C 的坐标，用待定系数法可求出直线 DC 的解析式，而 AB∥DC， 则直线 AB 与 DC 的斜率相同，再加上 A 点的坐标，即可求出直线 AB 的解析式，联立直线 AB 和抛物线的 解析式，可求出 B 点的坐标，即可得出 AB、AC 的长．在 Rt△ABC 和 Rt△AMG 中，已知了 ∠BAC=∠AGM=90°，若两三角形相似，则直角边对应成比例，据此可求出 M 点的坐标． 【详解】易知：A(−1,0),D(1,0),C(0,−1) ； 则 OA=OD=OC=1 ， ∴△ADC 是等腰直角三角形， ∴∠ACD=90 ° ,AC= 2 ； 又∵AB ∥DC ， ∴∠BAC=90 ° ； 易知直线 BD 的解析式为 y=x−1 ， 由于直线 AB ∥DC, 可设直线 AB 的解析式为 y=x+b, 由于直线 AB 过点 A(−1,0) ； 则直线 AB 的解析式为：y=x+1 ， 联立抛物线的解析式： 2 1     1 y x y x      ， 解得 2 3 x y    , 1 0 x y     ； 故 B(2,3) ； ∴AP=  2 22 1 3  =3 2 ； Rt△BAC 和 Rt△AMG 中,∠AGM=∠PAC=90 ° , 且 BA:AC=3 2 : 2 =3:1 ； 若以 A. M 、G 三点为顶点的三角形与△BCA 相似，则 AG:MG=1:3 或 3:1 ； 设 M 点坐标为(m,m 2 −1),(m<−1 或 m>1) 则有：MG=m 2 −1 ，AG=|m+1| ； ①当 AM:MG=1:3 时,m 2 −1=3|m+1|,m 2 −1=±(3m+3) ； 当 m 2 −1=3m+3 时,m 2 −3m−4=0, 解得 m=1( 舍去) ，m=4 ； 当 m 2 −1=−3m−3 时,m 2 +3m+2=0, 解得 m=−1( 舍去) ，m=−2 ； ∴M 1 (4,15),M 2 (−2,3) ； ②当 AM:MG=3:1 时,3(m 2 −1)=|m+1|,3m 2 −3=±(m+1) ； 当 3m 2 −3=m+1 时,3m 2 −m−4=0, 解得 m=−1( 舍去),m= 4 3 ； 当 3m 2 −3=−m−1 时,3m 2 +m−2=0, 解得 m=−1( 舍去),m= 2 3 ( 舍去) ； ∴M 3 ( 4 3 , 7 9 ). 故符合条件的 M 点坐标为：(4,15),(−2,3), ( 4 3 , 7 9 ). 故答案为：:(4,15),(−2,3), ( 4 3 , 7 9 ). 【点睛】本题考查了二次函数，解题的关键是熟练的掌握二次函数的性质与应用. 4．如图，直线 y=x+2 与抛物线 y=ax2+bx+6（a≠0）相交于 A（ ， ）和 B（4，m），点 P 是线段 AB 上 异于 A、B 的动点，过点 P 作 PC⊥x 轴于点 D，交抛物线于点 C．当△PAC 为直角三角形时点 P 的坐 标 ． 【答案】（3，5）或（ 7 2 ，11 2 ）． 【解析】 试题分析：由于 P 点不可能为直角顶点，因此就只有两种情况：若 A 为直角顶点，过 A 作 AB 的垂线与抛 物线的交点即为 C 点，过 C 作 y 轴的平行线与 AB 的交点即为 P 点；若 C 为直角顶点，过 A 作 x 轴的平行 线与抛物线的另一个交点即为 C 点，过 C 作 y 轴的平行线与 AB 的交点即为 P 点． 解：∵直线 y=x+2 过点 B（4，m）， ∴m=6， ∴B（4，6）． 将 A、B 两点坐标代入抛物线解析式得： ， 解得： ∴抛物线的解析式为：y=2x2﹣8x+6． ①若 A 为直角顶点，如图 1， 设 AC 的解析式为：y=﹣x+b， 将 A 点代入 y=﹣x+b 得 b=3 ∴AC 的解析式为 y=﹣x+3， 由 ，解得： 或 （舍去） 令 P 点的横坐标为 3，则纵坐标为 5， ∴P（3，5）； ②若 C 为直角顶点，如图 2， 令 ，解得：x= 或 x= （舍去）， 令 P 点的横坐标为 ，则纵坐标为 ， ∴P（ ， ）； 故答案为（3，5）或（ ， ）． 考点：二次函数综合题． 5．如图，已知抛物线  22 1y x   与 x 轴交于 A、C 两点，与 y 轴交于点 B，在抛物线的对称轴 上找一点 Q，使△ABQ 成为等腰三角形，则 Q 点的坐标是____. 【答案】Q1  2 3 6， ，Q2  2 3 6， ，Q3（2，2），Q4（2，3） 【解析】先求得点 A 和点 B 的坐标，由顶点式知抛物线的对称轴为直线 x=2，设抛物线的对称轴上的点 Q 的坐标为  2 m， ，分别求得 AB ，并用含 m 的代数式表示 BQ AQ、 的长，分 AB BQ BQ AQ AB AQ  ， ， 三种情况构造方程求得 m 的值. 【详解】如图， 抛物线的对称轴为直线 x=2 当 y=0 时， （x-2）2-1=0 解之：x1=3，x2=1 ∴点 A 的坐标为（1，0） 当 x=0 时，y=3 ∴点 B（0，3） 设点 Q 的坐标为（2，m）. ∴AB2=32+1=10，BQ2=（m-3）2+22=（m-3）2+4，AQ2=m2+1， 要使△ABQ 为等腰三角形， 当 AB2=BQ2 时，则（m-3）2+4=10, 解之：m1=3 6 ， m2=3 6 ， ∴点 Q1  2 3 6， ， Q2  2 3 6， . 当 BQ2=AQ2 时，则（m-3）2+4=m2+1, 解之：m=2 所以点 Q2（2，2）； 当 AB2=AQ2 时，则 10=m2+1, 解之：m=±3 若 m=-3，则点 B、A，Q 在同一直线上， ∴m=-3 舍去， ∴点 Q4（2，3） 故答案为： 2 3 6， ，Q2  2 3 6， ，（2，2），（2，3） 【点睛】本题考查了二次函数的图象与性质、勾股定理、等腰三角形的判定等知识点．难点在于符合条件 的等腰三角形可能有多种情形，需要分类讨论． 6．如图，抛物线 y＝﹣x2+2x+4 与 y 轴交于点 C，点 D（0，2），点 M 是抛物线上的动点．若△MCD 是以 CD 为底的等腰三角形，则点 M 的坐标为_____． 【答案】（1+ 2 ，3）或（1﹣ 2 ，3） 【解析】当△MCD 是以 CD 为底的等腰三角形时，则 M 点在线段 CD 的垂直平分线上，由 C、D 坐标可求 得线段 CD 中点的坐标，从而可知 P 点的纵坐标，代入抛物线解析式可求得 M 点坐标． 【详解】△MCD 是以 CD 为底的等腰三角形， 点 M 在线段 CD 的垂直平分线上， 如图，过 M 作 ME y 轴于点 E，则 E 为线段 CD 的中点， 抛物线 2 2 4y x x    与 y 轴交于点 C， C(0,4),且 D(0,2)， E 点坐标为(0,3)， M 点纵坐标为 3， 在 2 2 4y x x    中,令 3y  ,可得 2 2 4 3x x    ,解得 1 2x   ， M 点坐标为 (1 2,3) 或 (1 2,3) ， 故答案为 (1 2,3) 或 (1 2,3) . 【点睛】本题考查的知识点是二次函数图像上点的坐标特征，等腰三角形的性质，解题关键是利用等腰三 角形三线合一的性质进行解答. 7．如图，在平面直角坐标系 xOy 中，已知抛物线 y=﹣x2+2x+3 与 x 轴交于 A，B 两点，点 M 在这条抛物 线上，点 P 在 y 轴上，如果四边形 ABMP 是平行四边形，则点 M 的坐标为______． 【答案】（4，-5）. 【解析】根据抛物线 y=﹣x2+2x+3 与 x 轴交于 A，B 两点，可求出 A、B 两点的坐标，进而求出 AB 的长度， 由四边形 ABMP 是平行四边形，可知 M 点在 x 轴右边，PM//AB，且 PM=AB=4 ，即可求出 M 点坐标. 【详解】∵y=﹣x2+2x+3 与 x 轴交于 A，B 两点， ∴A（-1，0）；B（3，0） ∴AB=4， ∵四边形 ABMP 是平行四边形， ∴AB//PM，PM=AB=4， ∵P 点在 y 轴上， ∴P 点横坐标为 4， ∵P 点在抛物线 y=﹣x2+2x+3 上， ∴x=4 时，y=-16+8+3=-5， ∴M 点的坐标为：（4，-5）. 故答案为（4，-5） 【点睛】本题考查二次函数的应用，求出 A、B 的长度利用 AB=PM 求出 M 的横坐标是解题关键. 8．已知抛物线 y＝（x﹣2）2，P 是抛物线对称轴上的一个点，直线 x＝t 分别与直线 y＝x、抛物线交于点 A，B，若△ABP 是等腰直角三角形，则 t 的值为_____． 【答案】0 或 3 或 2 2 或 3± 3 或 7 17 2  【解析】首先求出抛物线与直线 y=x 的交点坐标，再分四种情形列出方程即可解决问题． 【详解】解：由题意 A（t，t），P（2，m）B[t，（t﹣2）2]， 当点 A 或 B 是直角顶点时，|2﹣t|＝|t﹣（t﹣2）2|， 解得 t＝3± 3 或 2± 2 ， 当点 P 是直角顶点时，|t﹣（t﹣2）2|＝2•|2﹣t|， 解得 t＝ 7 17 2  或 0 或 3， 综上所述，满足条件的 t 的值为 0 或 3 或 2± 2 或 3± 15 或 7 17 2  ． 故答案是：0 或 3 或 2 2 或 3± 3 或 7 17 2  ． 【点睛】考查二次函数的性质、一次函数的应用、等腰直角三角形的性质、一元二次方程等知识，解题的 关键是学会用转化的思想思考问题，学会构建方程解决问题. 9．将抛物线 2 1y x 向右平移 2 个单位,得到抛物线 2y 的图象.P 是抛物线 2y 对称轴上的一个动点,直线 x t 平行于 y 轴,分别与直线 y x 、抛物线 2y 交于点 A、 B.若 ABP 是以点 A 或点 B 为直角顶点的等腰直角 三角形,求满足条件的 t 的值,则 t  ______ . 【答案】3 3 或3 3 或 2 2 或 2 2 【解析】根据函数图象的平移规律，将 1y 向右平移 2 个单位,横坐标减 2 表示出抛物线 2y 的函数解析式.然 后再根据题目条件表示出点 A、B 的坐标,进而能够表示出 AB 的长度与 AP 的长度,然后根据等腰直角三角 形的两直角边相等列出方程求解即可. 【详解】解：抛物线 2 1y x 向右平移 2 个单位, 抛物线 2y 的函数解析式为 2 2y (x 2) x 4x 4     , 抛物线 2y 的对称轴为直线 x 2 , 直线 x t 与直线 y x 、抛物线 2y 交于点 A、B, 点 A 的坐标为 t,t ,点 B 的坐标为 2t,t 4t 4  , 2 2AB t 4t 4 t t 5t 4        , AP t 2  , APB 是以点 A 或 B 为直角顶点的三角形, 2t 5t 4 t 2     , 2t 5t 4 t 2     ①或  2t 5t 4 t 2     ②, 整理 ① 得, 2t 6t 6 0   , 解得 1t 3 3  , 2t 3 3  , 整理 ② 得, 2t 4t 2 0   , 解得 1t 2 2  , 2t 2 2  , 综上所述,满足条件的 t 值为：3 3 或3 3 或 2 2 或 2 2 , 故答案为：3 3 或 3 3 或 2 2 或 2 2 . 【点睛】本题考查了二次函数图象与几何变换,等腰直角三角形的性质,根据抛物线与直线的解析式表示出 AB、AP 或 BP 的长,然后根据等腰直角三角形的性质列出方程是解题的关键. 10．如图，已知抛物线 21 44y x bx    与 x 轴相交于 A 、 B 两点，与 y 轴相交于点 C ．若已知 A 点的 坐标为  2,0A  ．点Q 在抛物线的对称轴上，当 ACQ 为等腰三角形时，点Q 的坐标为________． 【答案】 3,0 ， 3,4 11 ， 3,4 11 【解析】首先求出抛物线解析式，然后利用配方法或利用公式 x=- 2 b a 求出对称轴方程，由此可设可设点 Q （3，t），若△ACQ 为等腰三角形，则有三种可能的情形，需要分类讨论，逐一计算，避免漏解． 【详解】∵抛物线 y=- 1 4 x2+bx+4 的图象经过点 A（-2，0）， ∴- 1 4 ×（-2）2+b×（-2）+4=0， 解得：b= 3 2 ， ∴抛物线解析式为 y=- 1 4 x2+ 3 2 x+4， 又∵y=- 1 4 x2+ 3 2 x+4=- 1 4 （x-3）2+ 25 4 ， ∴对称轴方程为：x=3， ∴可设点 Q（3，t），则可求得： AC= 2 22 4 2 5  ， AQ= 2 25 t ， CQ=  223 4t  ． i）当 AQ=CQ 时， 有 2 25 t =  223 4t  ， 即 25+t2=t2-8t+16+9， 解得 t=0， ∴Q1（3，0）； ii）当 AC=AQ 时， 有 2 25 t =2 5 ， 即 t2=-5，此方程无实数根， ∴此时△ACQ 不能构成等腰三角形； iii）当 AC=CQ 时， 有 2 5 =  223 4t  ， 整理得：t2-8t+5=0， 解得：t=4± 11 ， ∴点 Q 坐标为：Q2（3，4+ 11 ），Q3（3，4- 11 ）． 综上所述，存在点 Q，使△ACQ 为等腰三角形，点 Q 的坐标为：Q1（3，0），Q2（3，4+ 11 ），Q3（3， 4- 11 ）． 故答案为：（3，0），（3，4+ 11 ），（3，4- 11 ）． 【点睛】本题考查了二次函数与一次函数的图象与性质、待定系数法、勾股定理、等腰三角形的判定等知 识点．难点在于符合条件的等腰三角形△ACQ 可能有多种情形，需要分类讨论． 11．如图，抛物线 21 1 32 2y x x   与 x 轴的负半轴交于点 A ，与 y 轴交于点 B ，连接 AB ，点 ,D E 分别 是直线 1x   与抛物线上的点，若点 , , ,A B D E 围成的四边形是平行四边形，则点 E 的坐标为__________. 【答案】 4,3 或 2,0 或 2, 2  【解析】根据二次函数 21 1y= x x 32 2  与 x 轴的负半轴交于点 A ，与 y 轴交于点 B .直接令 x=0 和 y=0 求出 A，B 的坐标.再根据平行四边形的性质分情况求出点 E 的坐标. 【详解】由抛物线的表达式求得点 ,A B 的坐标分别为   3,0 , 0, 3  . 由题意知当 AB 为平行四边形的边时， / /AB DE ，且 AB DE ， ∴线段 DE 可由线段 AB 平移得到. ∵点 D 在直线 1x   上，①当点 B 的对应点为 1D 时，如图，需先将 AB 向左平移 1 个单位长度， 此时点 A 的对应点 1E 的横坐标为 4 ，将 4x   代入 21 1 32 2y x x   ， 得 3y  ，∴ 1( 4,3)E  . ②当点 A 的对应点为 2D 时，同理，先将 AB 向右平移 2 个单位长度，可得点 B 的对应点 2E 的横坐标为 2， 将 2x  代入 21 1 32 2y x x   得 0y  ，∴ 2 (2,0)E 当 AB 为平行四边形的对角线时，可知 AB 的中点坐标为 1 3,2 2      ， ∵ 3D 在直线 1x   上， ∴根据对称性可知 3E 的横坐标为 2 ，将 2x   代入 21 1 32 2y x x   得 2y   ，∴ 3 ( 2, 2)E   . 综上所述，点 E 的坐标为  4,3 或 2,0 或 2, 2  . 【点睛】本题是二次函数的综合题，主要考查了特殊点的坐标的确定，平行四边形的性质，解本题的关键 是分情况解决问题的思想． 三、解答题 12．如图，抛物线 与直线 交于 A，B 两点，交 x 轴于 D，C 两点，已知 ， ． 求抛物线的函数表达式并写出抛物线的对称轴； 在直线 AB 下方的抛物线上是否存在一点 E，使得 的面积最大？如果存在，求出 E 点坐标；如果 不存在，请说明理由． 为抛物线上一动点，连接 PA，过点 P 作 交 y 轴于点 Q，问：是否存在点 P，使得以 A、P、Q 为顶点的三角形与 相似？若存在，请直接写出所有符合条件的 P 点的坐标；若不存在，请说明理由． 【答案】（1） （2）当 时， 的面积有最大值 4，此时 E 点坐标为 （3） 满足条件的 P 点坐标为 或 或 或 【解析】 利用待定系数法求抛物线解析式，根据抛物线的对称轴方程求抛物线的对称轴； 先确定直线 AB 的解析式为 ，再解方程组 得 ，作 轴交直线 AB 于 F，如图 1，设 ，则 ，则 ，利用三角形面 积公式得到 ，然后根据二次函数的性质解决问题； 设 ，则 ，先利用勾股定理的逆定理判断 为直角三角形，利用相 似三角形的判定方法，当 ， ∽ ，则 ，所以 ；当 ， ∽ ，即 ，所以 ，然后分别解关于 t 的绝对值方 程即可得到 P 点坐标． 【详解】 把 ， 代入 得 ，解得 ， 抛物线解析式为 ； 抛物线的对称轴为直线 ； 存在． 把 代入 得 ， 直线 AB 的解析式为 ， 解方程组 得 或 ，则 ， 作 轴交直线 AB 于 F，如图 1， 设 ，则 ， ， ， 当 时， 的面积有最大值 4，此时 E 点坐标为 ； 设 ，则 ， ， ， ， ， ， ， ， 为直角三角形， ， 当 ， ∽ ， 即 ， ， 解方程 得 舍去 ， ，此时 P 点坐标为 ； 解方程 得 舍去 ， ，此时 P 点坐标为 ； 当 ， ∽ ， 即 ， ， 解方程 得 舍去 ， ，此时 P 点坐标为 ； 解方程 得 舍去 ， ，此时 P 点坐标为 ； 综上所述，满足条件的 P 点坐标为 或 或 或 【点睛】本题是二次函数的综合题：熟练掌握二次函数图象上点的坐标特征、二次函数的性质和相似三角 形的判定与性质；会利用待定系数法求函数解析式；理解坐标与图形性质，记住两点间的距离公式；会运 用分类讨论的思想解决数学问题． 13．如图，抛物线 经过点 A（-1,0）、B（3,0）、C（0， ），连接 AC、BC，将△ABC 绕 点 C 逆时针旋转，使点 A 落在 x 轴上，得到△DCE，此时，DE 所在直线与抛物线交于第一象限的点 F. （1）求抛物线 对应的函数关系式. （2）求点 A 所经过的路线长. （3）抛物线的对称轴上是否存在点 P 使△PDF 是等腰三角形. 若存在，求点 P 的坐标；若不存在，说明理由. 【答案】（1） （2） （3）P（1,2），（1，-2），（1,2 ） 或（1， 【解析】 试题分析：（1）抛物线 经过点 A（-1,0）、B（3,0）、C（0， ），那么 0 9 3 0 3 a b c a b c c           ，解得 3 3 2 3 3 3 a b c           ，所以抛物线 对应的函数关系式为 （2）将△ABC 绕点 C 逆时针旋转，使点 A 落在 x 轴上，得到△DCE，则 D 的坐标（1，0）。所以 AD=1+1=2， 点 A（-1,0）、C（0， ），在 ,AOC COD  ， ,AOC COD  是直角，AO=1，CO= ，由勾股定理得  221 3 2AC    ，同理 CD=2，所以三角形 ACD 是等边三角形， 60ACD   ；点 A 所经过的路线 是一个扇形的弧长，圆心角为 60ACD   ，半径为 AC=2 所以扇形的弧长= （3）抛物线的对称轴上存在点 P 使△PDF 是等腰三角形，抛物线 的对称轴 2 3 3 12 32 3 bx a            ；设点 P 的坐标为（1，a），F 的坐标为（x,y），则 P、D 都在抛物线的对称轴 上; 假设△PDF 是等腰三角形，FD 是腰，则 PD=FD，由（1）知 D 的坐标（1，0），所以 PD= a ，FD=  2 21x y  ,则 a =  2 21x y  ，而点 F 在抛物线上，所以 F 的坐标满足的解析式 ，解得 2a   ；当△PDF 是等腰三角形，FD 是底边，那么 PF、PD 是腰，所 以 PF=PD，则 PD= a ，F 的坐标为（x,y），F 的坐标满足的解析式 ；PF=    2 21y a x   ，则 a =    2 21y a x   ，解得 a=2 或 a= 2 3 3 ,所以 P 点的坐标为 P（1,2）， （1，-2），（1,2 ）或（1， 考点：抛物线，等腰三角形 点评：本题考查抛物线，等腰三角形，要求考生会用待定系数法求函数的解析式，掌握抛物线的性质，熟 悉等腰三角形的性质 14．如图，抛物线经过原点 O（0，0），点 A（1，1），点 B（ 7 2 ，0）． （1）求抛物线解析式； （2）连接 OA，过点 A 作 AC⊥OA 交抛物线于 C，连接 OC，求△AOC 的面积； （3）点 M 是 y 轴右侧抛物线上一动点，连接 OM，过点 M 作 MN⊥OM 交 x 轴于点 N．问：是否存在点 M，使以点 O，M，N 为顶点的三角形与（2）中的△AOC 相似，若存在，求出点 M 的坐标；若不存在， 说明理由． 【答案】（1） 22 7 5 5y x x   ；（2）4；（3）（ 27 2 ，﹣54）或（ 23 8 ， 23 32 ）或（ 33 8 ，﹣ 33 32 ） 【解析】 分析：（1）设交点式 y=ax（x- 7 2 ），然后把 A 点坐标代入求出 a 即可得到抛物线解析式； （2）延长 CA 交 y 轴于 D，如图 1，易得 OA= 2 ，∠DOA=45°，则可判断△AOD 为等腰直角三角形，所 以 OD= 2 OA=2，则 D（0，2），利用待定系数法求出直线 AD 的解析式为 y=-x+2，再解方程组 2 2 2 7 5 5 y x y x x     ＝ ＝ ，得 C（5，-3），然后利用三角形面积公式，利用 S△AOC=S△COD-S△AOD 进行计算； （3）如图 2，作 MH⊥x 轴于 H，AC=4 2 ，OA= 2 ，设 M（x，- 2 5 x2+ 7 5 x）（x＞0），根据三角形相似 的判定，由于∠OHM=∠OAC，则当 OH MH OA AC  时，△OHM∽△OAC，即 22 7 5 5 2 4 2 x xx    ；当 OH MH AC OA  时，△OHM∽△CAO，即 22 7 5 5 4 2 2 x xx    ，则分别解关于 x 的绝对值方程可得到对应 M 点的坐标，由于△OMH∽△ONM，所以求得的 M 点能以点 O，M，N 为顶点的三角形与（2）中的△AOC 相似． 详解：（1）设抛物线解析式为 y=ax（x- 7 2 ）， 把 A（1，1）代入得 a•1（1- 7 2 ）=1，解得 a=- 2 5 ， ∴抛物线解析式为 y=- 2 5 x（x- 7 2 ）， 即 y=- 2 5 x2+ 7 5 x； （2）延长 CA 交 y 轴于 D，如图 1， ∵A（1，1）， ∴OA= 2 ，∠DOA=45°， ∴△AOD 为等腰直角三角形， ∵OA⊥AC， ∴OD= 2 OA=2， ∴D（0，2）， 易得直线 AD 的解析式为 y=-x+2， 解方程组 2 2 2 7 5 5 y x y x x     ＝ ＝ 得 1 1 x y ＝ ＝    或 5 3 x y    ＝ ＝ ，则 C（5，-3）， ∴S△AOC=S△COD-S△AOD= 1 2 ×2×5- 1 2 ×2×1=4； （3）存在．如图 2， 作 MH⊥x 轴于 H，AC= 2 2(5 1) ( 3 1) =4 2    ，OA= 2 ， 设 M（x，- 2 5 x2+ 7 5 x）（x＞0）， ∵∠OHM=∠OAC， ∴当 OH MH OA AC  时，△OHM∽△OAC，即 22 7 5 5 2 4 2 x xx    ， 解方程- 2 5 x2+ 7 5 x =4x 得 x1=0（舍去），x2=- 13 2 （舍去）， 解方程- 2 5 x2+ 7 5 x =-4x 得 x1=0（舍去），x2= 27 2 ，此时 M 点坐标为（ 27 2 ，-54）； 当 OH MH AC OA  时，△OHM∽△CAO，即 22 7 5 5 4 2 2 x xx    ， 解方程- 2 5 x2+ 7 5 x= 1 4 x 得 x1=0（舍去），x2= 23 8 ，此时 M 点的坐标为（ 23 8 ， 23 32 ）， 解方程- 2 5 x2+ 7 5 x=- 1 4 x 得 x1=0（舍去），x2= 33 8 ，此时 M 点坐标为（ 33 8 ，- 33 32 ）； ∵MN⊥OM， ∴∠OMN=90°， ∴∠MON=∠HOM， ∴△OMH∽△ONM， ∴当 M 点的坐标为（ 27 2 ，-54）或（ 23 8 ， 23 32 ）或（ 33 8 ，- 33 32 ）时，以点 O，M，N 为顶点的三角形与 （2）中的△AOC 相似． 点睛：本题考查了二次函数的综合题：熟练掌握二次函数图象上点的坐标特征和二次函数的性质；会利用 待定系数法求函数解析式，会解一元二次方程；理解坐标与图形性质；灵活运用相似比表示线段之间的关 系；会运用分类讨论的思想解决数学问题． 15．如图，已知抛物线 与 轴交于 两点，与 轴交于 点，且 ，直 线 与 轴交于 点，点 是抛物线 上的一动点，过点 作 轴， 垂足为 ，交直线 于点 . （1）试求该抛物线的表达式； （2）如图（1），若点 在第三象限，四边形 是平行四边形，求 点的坐标； （3）如图（2），过点 作 轴，垂足为 ，连接 ， ①求证： 是直角三角形； ②试问当 点横坐标为何值时，使得以点 为顶点的三角形与 相似？ 【答案】（1）y= x2+ x﹣4；（2）点 P 的坐标为（﹣ ，﹣ ）或（﹣8，﹣4）；（3）①详见解析；②， 点 P 的横坐标为﹣5.5 或﹣10.5 或 2 或﹣18 时，使得以点 P、C、H 为顶点的三角形与△ACD 相似． 【解析】 试题分析：（1）将点 A 和点 C 的坐标代入抛物线的解析式可得到关于 a、c 的方程组，然后解方程组求得 a、 c 的值即可；（2）设 P（m， m2+ m﹣4），则 F（m，﹣ m﹣4），则 PF=﹣ m2﹣ m，当 PF=OC 时， 四边形 PCOF 是平行四边形，然后依据 PF=OC 列方程求解即可；（3）①先求得点 D 的坐标，然后再求得 AC、DC、AD 的长，最后依据勾股定理的逆定理求解即可；②分为△ACD∽△CHP、△ACD∽△PHC 两种 情况，然后依据相似三角形对应成比例列方程求解即可 试题解析： （1）由题意得： ，解得： ， ∴抛物线的表达式为 y= x2+ x﹣4． （2）设 P（m， m2+ m﹣4），则 F（m，﹣ m﹣4）． ∴PF=（﹣ m﹣4）﹣（ m2+ m﹣4）=﹣ m2﹣ m． ∵PE⊥x 轴， ∴PF∥OC． ∴PF=OC 时，四边形 PCOF 是平行四边形． ∴﹣ m2﹣ m=4，解得：m=﹣ 或 m=﹣8． 当 m=﹣ 时， m2+ m﹣4=﹣ ， 当 m=﹣8 时， m2+ m﹣4=﹣4． ∴点 P 的坐标为（﹣ ，﹣ ）或（﹣8，﹣4）． （3）①证明：把 y=0 代入 y=﹣ x﹣4 得：﹣ x﹣4=0，解得：x=﹣8． ∴D（﹣8，0）． ∴OD=8． ∵A（2，0），C（0，﹣4）， ∴AD=2﹣（﹣8）=10． 由两点间的距离公式可知：AC2=22+42=20，DC2=82+42=80，AD2=100， ∴AC2+CD2=AD2． ∴△ACD 是直角三角形，且∠ACD=90°． ②由①得∠ACD=90°． 当△ACD∽△CHP 时， ，即 或 ， 解得：n=0（舍去）或 n=﹣5.5 或 n=﹣10.5． 当△ACD∽△PHC 时， ，即 或 ． 解得：n=0（舍去）或 n=2 或 n=﹣18． 综上所述，点 P 的横坐标为﹣5.5 或﹣10.5 或 2 或﹣18 时，使得以点 P、C、H 为顶点的三角形与△ACD 相 似． 考点：二次函数综合题. 16．如图，顶点为 M 的抛物线 2 3y ax bx   与 x 轴交于  3,0A ，  1,0B  两点，与 y 轴交于点C ． （1）求这条抛物线对应的函数表达式； （2）问在 y 轴上是否存在一点 P ，使得 PAM 为直角三角形？若存在，求出点 P 的坐标；若不存在，说 明理由． （3）若在第一象限的抛物线下方有一动点 D ，满足 DA OA ，过 D 作 DG x 轴于点G ，设 ADG 的 内心为 I ，试求 CI 的最小值． 【答案】（1） 2y x 2x 3    ；（2）点 P 坐标为 30, 2     或 0,1 或 0,3 或 70, 2      时， PAM 为直角三 角形；（3）CI 最小值为 3 10 3 2 2  . 【解析】（1）结合题意，用待定系数法即可求解； （2）分 3 种情况讨论，用勾股定理即可求解； （3）根据正方形的判定和勾股定理，即可得到答案. 【详解】（1）∵抛物线 2 3y ax bx   过点  3,0A ，  1,0B  ， ∴ 9 3 3 0 3 0 a b a b        ，解得： 1 2 a b     ， ∴这条抛物线对应的函数表达式为 2y x 2x 3    . （2）在 y 轴上存在点 P ，使得 PAM 为直角三角形． ∵  22 2 3 1 4y x x x        ， ∴顶点  1,4M ， ∴  22 23 1 4 20AM     ， 设点 P 坐标为 0, p ， ∴ 2 2 2 23 9AP p p    ，  22 2 21 4 17 8MP p p p      ， ①若 90PAM   ，则 2 2 2AM AP MP  . ∴ 2 220 9 17 8p p p     ， 解得： 3 2p   ， ∴ 30, 2P    . ②若 90APM   ，则 2 2 2AP MP AM  ， ∴ 2 29 17 8 20p p p     ， 解得： 1 1p  ， 2 3p  ， ∴  0,1P 或 0,3 . ③若 90AMP   ，则 2 2 2AM MP AP  ， ∴ 2 220 17 8 9p p p     ， 解得： 7 2p  ， ∴ 70, 2P     . 综上所述，点 P 坐标为 30, 2     或 0,1 或 0,3 或 70, 2      时， PAM 为直角三角形． （3）如图，过点 I 作 IE x 轴于点 E ， IF AD 于点 F ， IH DG 于点 H ， ∵ DG x 轴于点G ， ∴ 90HGE IEG IHG       ， ∴四边形 IEGH 是矩形， ∵点 I 为 ADG 的内心， ∴ IE IF IH  ， AE AF ， DF DH ， EG HG ， ∴矩形 IEGH 是正方形， 设点 I 坐标为 ,m n ， ∴OE m ， HG GE IE n   ， ∴ 3AF AE OA OE m     ， ∵ 3DA OA  ， ∴  3 3DH DF DA AF m m       ， ∴ DG DH HG m n    ， ∵ 2 2 2DG AG DA  ， ∴   2 2 23 3m n n m     ， ∴化简得： 2 23 3 0m m n n    ， 配方得： 2 23 3 9 2 2 2m n             ， ∴点  ,I m n 与定点 3 3,2 2Q    的距离为 3 2 2 . ∴点 I 在以点 3 3,2 2Q    为圆心，半径为 3 2 2 的圆在第一象限的弧上运动， ∴当点 I 在线段CQ 上时， CI 最小， ∵ 2 23 3 3 1032 2 2CQ              ， ∴ 3 10 3 2 2CI CQ IQ    ， ∴CI 最小值为 3 10 3 2 2  . 【点睛】本题考查用待定系数法求二元一次方程、勾股定理和正方形的判定，解题的关键是熟练掌握用待 定系数法求二元一次方程、勾股定理和正方形的判定. 17．如图，已知抛物线 y=-x2+bx+c 经过点 A（-1，0）和 C（0，4）． （1）求这条抛物线的解析式； （2）直线 y=x+1 与抛物线相交于 A、D 两点，点 P 是抛物线上一个动点，点 P 的横坐标是 m，且-1＜m＜ 3，设△ADP 的面积为 S，求 S 的最大值及对应的 m 值； （3）点 M 是直线 AD 上一动点，直接写出使△ACM 为等腰三角形的点 M 的坐标． 【答案】（1）y=-x2+3x+4；（2）当 m=1 时，△ADP 的面积 S 的最大值为 8．（3） 1 34 341,2 2M      ． 2 34 341,2 2M        ，  3 4,5M ， 4 7 17 10 1, 0M      . 【解析】 【详解】解：（1）A（-1，0）和 C（0，4）代入 y=-x2+bx+c， 得 1 0 4 b c c      ＝ ＝ ， 解得 3 4 b c ＝ ＝    ， ∴此抛物线解析式为：y=-x2+3x+4．（2）由题意得： 2 1 3 4 y x y x x      ＝ ＝ , ， 解得： 1 1 1 0 x y    ＝ ＝ 或, 2 2 3 4 x y    ， ∴点 D 的坐标为（3，4）， 过点 P 作 PQ∥y 轴，交直线 AD 与点 Q， ∵点 P 的横坐标是 m， 又点 P 在抛物线 y=-x2+3x+4 ∴P 的纵坐标是-m2+3m+4，点 Q 的横坐标也是 m， ∵点 Q 在直线 y=x+1 上， ∴Q 的纵坐标是 m+1， ∴PQ=（-m2+3m+4）-（m+1）=-m2+2m+3， S△ADP=S△APQ+S△DPQ= 1 2 (−m2+2m+3)[m−(−1)]+(−m2+2m+3)(3−m)， = 1 2 (−m2+2m+3)×4， =-2m2+4m+6， =-2（m-1）2+8， 当 m=1，△ADP 的面积 S 的最大值为 8． （3）∵M 在直线 AD：y=x+1 上，设 M 点坐标为（x，x+1）， ∵A（-1，0）和 C（0，4）； ∴AC2=17，AM2=2(x+1)2，CM2=x2+（x-3）2， Ⅰ.当 AC=AM 时，17=2(x+1)2，解得 x= 34 12   ， 即点 M 坐标为： 1 34 341,2 2M      ， 2 34 341,2 2M        Ⅱ.当 AC=CM 时，x2+（x-3）2=17，解得： 1 4x  ， 2 1x   （与 A 重合舍去）， 即点 M 坐标为：  3 4,5M ， III.当 AC=AM 时，2(x+1)2=x2+（x-3）2，解得：x= 7 10 ， 即点 M 坐标为： 4 7 17 10 1, 0M      ， 使△ACM 为等腰三角形的点 M 的坐标有 1 34 341,2 2M      ． 2 34 341,2 2M        ，  3 4,5M ， 4 7 17 10 1, 0M      . 【点睛】此题主要考查了待定系数法求二次函数解析式以及二次函数最值求法和平面内两点之间的距离求 法等知识，二次函数这部分经常利用数形结合以及分类讨论思想相结合，综合性较强注意不要漏解． 18．在平面直角坐标系中有 Rt AOB ，O 为原点， 1OB  ， 3OA  ，将此三角形绕点 O 顺时针旋转90 得到 Rt COD ，抛物线 2y x bx   c 过 , ,A B C 三点． （1）求此抛物线的解析式及顶点 P 的坐标； （2）直线 : 3l kx k   与抛物线交于 ,M N 两点，若 2PMNS  ，求 k 的值； （3）抛物线的对称轴上是否存在一点Q 使得 DCQ 为直角三角形． 【答案】（1） 2y x 2x 3    ；点  1,4P ；（2） 2 3k   ；（3）存在，Q1(1，-1)，Q2(1，2)， Q3(1， 4)， Q4(1，-5)． 【解析】（1）用待定系数法可求抛物线的解析式，进行配成顶点式即可写出顶点坐标； （2）将直线与抛物线联立，通过根与系数关系得到 2M Nx x k   ， M Nx x k  ，再通过 2PMNS  得出 4M Nx x   ，通过变形得出 2 4 16M N M Nx x x x   代入即可求出 k 的值； （3）分： 90DQCÐ = ° ， 90QDC   ， 90DCQ   三种情况分别利用勾股定理进行讨论即可． 【详解】（1）∵ 1OB  ， 3OA  ， (0,3), ( 1,0)A B  ∵ Rt AOB 绕点O 顺时针旋转90 ，得到 Rt COD ， OA OC  ∴点C 的坐标为： 3,0 ， 将点 A,B 代入抛物线 2y x bx c    中得 3 1 0 c b c      解得 2 3 b c    ∴此抛物线的解析式为： 2y x 2x 3    ∵ 2 22 3 ( 1) 4y x x x        ； ∴点  1,4P （2）直线l ： 3y kx k   与抛物线的对称轴交点 F 的坐标为 1,3 ， 交抛物线于  ,M MM x y ，  ,N NN x y ， 1PF  由 2 3 2 3 y kx k y x x         得： 2 ( 2) 0x k x k    ∴ 2M Nx x k   ， M Nx x k  ∵ 2PMNS  ， ∴ 1 11· 1· 22 2M Nx PF x PF    ∴1 1 4M Nx x    ∴ 4M Nx x   ∴ 2 4 16M N M Nx x x x   ∴ 2 3k   （3）存在， 1t   或 2t  ， 4t  ， 5t   (3,0) (0,1)C D ∴ 2 2 2 10CD OC OD   设点  1,Q t 2 2 22CQ t  ，  22 21 1DQ t   若 90DQCÐ = ° ，则 2 2 2CD CQ DQ  即 2 2 2 22 1 ( 1) 10t t     ∴ 1t   或 2t  若 90QDC   ，则 2 2 2CQ DQ CD  即 2 2 2 22 t 1 (t 1) 10     ∴ 4t  若 90DCQ   ，则 2 2 2DQ CQ CD  即 2 2 2 22 t 10 1 (t 1)     ∴ 5t   即 Q1(1,-1), Q2(1,2), Q3(1,4), Q4(1,-5). 【点睛】本题主要考查二次函数与几何综合，掌握二次函数的图象和性质，分情况讨论是解题的关键． 19．如图，抛物线 y＝﹣x2﹣2x+3 的图象与 x 轴交于 A、B 两点(点 A 在点 B 的左边)，与 y 轴交于点 C， 点 D 为抛物线的顶点． (1)求点 A、B、C 的坐标； (2)点 M(m，0)为线段 AB 上一点(点 M 不与点 A、B 重合)，过点 M 作 x 轴的垂线，与直线 AC 交于点 E， 与抛物线交于点 P，过点 P 作 PQ∥AB 交抛物线于点 Q，过点 Q 作 QN⊥x 轴于点 N，可得矩形 PQNM．如 图，点 P 在点 Q 左边，试用含 m 的式子表示矩形 PQNM 的周长； (3)当矩形 PQNM 的周长最大时，m 的值是多少？并求出此时的△AEM 的面积； (4)在(3)的条件下，当矩形 PMNQ 的周长最大时，连接 DQ，过抛物线上一点 F 作 y 轴的平行线，与直线 AC 交于点 G(点 G 在点 F 的上方)．若 FG＝2 2 DQ，求点 F 的坐标． 【答案】(1)A(﹣3，0)，B(1，0)；C(0，3) ；(2)矩形 PMNQ 的周长＝﹣2m2﹣8m+2；(3) m＝﹣2；S＝ 1 2 ； (4)F(﹣4，﹣5)或(1，0)． 【解析】（1）利用函数图象与坐标轴的交点的求法，求出点 A，B，C 的坐标； （2）先确定出抛物线对称轴，用 m 表示出 PM，MN 即可； （3）由（2）得到的结论判断出矩形周长最大时，确定出 m，进而求出直线 AC 解析式，即可； （4）在（3）的基础上，判断出 N 应与原点重合，Q 点与 C 点重合，求出 DQ＝DC＝ 2 ，再建立方程（n+3） ﹣（﹣n2﹣2n+3）＝4 即可． 【详解】(1)由抛物线 y＝﹣x2﹣2x+3 可知，C(0，3)． 令 y＝0，则 0＝﹣x2﹣2x+3， 解得，x＝﹣3 或 x＝l， ∴A(﹣3，0)，B(1，0)． (2)由抛物线 y＝﹣x2﹣2x+3 可知，对称轴为 x＝﹣1． ∵M(m，0)， ∴PM＝﹣m2﹣2m+3，MN＝(﹣m﹣1)×2＝﹣2m﹣2， ∴矩形 PMNQ 的周长＝2(PM+MN)＝(﹣m2﹣2m+3﹣2m﹣2)×2＝﹣2m2﹣8m+2． (3)∵﹣2m2﹣8m+2＝﹣2(m+2)2+10， ∴矩形的周长最大时，m＝﹣2． ∵A(﹣3，0)，C(0，3)， 设直线 AC 的解析式 y＝kx+b， ∴ 3 0 3 k b b      解得 k＝l，b＝3， ∴解析式 y＝x+3， 令 x＝﹣2，则 y＝1， ∴E(﹣2，1)， ∴EM＝1，AM＝1， ∴S＝ 1 2 AM×EM＝ 1 2 ． (4)∵M(﹣2，0)，抛物线的对称轴为 x＝﹣l， ∴N 应与原点重合，Q 点与 C 点重合， ∴DQ＝DC， 把 x＝﹣1 代入 y＝﹣x2﹣2x+3，解得 y＝4， ∴D(﹣1，4)， ∴DQ＝DC＝ 2 ． ∵FG＝2 2 DQ， ∴FG＝4． 设 F(n，﹣n2﹣2n+3)，则 G(n，n+3)， ∵点 G 在点 F 的上方且 FG＝4， ∴(n+3)﹣(﹣n2﹣2n+3)＝4． 解得 n＝﹣4 或 n＝1， ∴F(﹣4，﹣5)或(1，0)． 【点睛】此题是二次函数综合题，主要考查了函数图象与坐标轴的交点的求法，待定系数法求函数解析式， 函数极值的确定，解本题的关键是用 m 表示出矩形 PMNQ 的周长． 20．如图，已知直线 1 22y x  与 x 轴交于点 B，与 y 轴交于点 C，抛物线 21 22y x bx   与 x 轴交于 A、B 两点（A 在 B 的左侧），与 y 轴交于点 C. （1）求抛物线的解析式； （2）点 M 是上述抛物线上一点，如果△ABM 和△ABC 相似，求点 M 的坐标； （3）连接 AC，求顶点 D、E、F、G 在△ABC 各边上的矩形 DEFC 面积最大时，写出该矩形在 AB 边上的 顶点的坐标． 【答案】（1） 21 3 22 2y x x   ；（2）M（3，-2）；（3）D( 3 2 ，0)或 D( 1 2  ，0)、E(2，0) 【解析】 试题分析：(1)先求得直线 1 22y x  与 x 轴交于点 B 与 y 轴交于点 C 的坐标，再把点 B 的坐标代入 21 22y x bx   ，求得 b 值，即可得抛物线的解析式；（2）先判定△ABC 为直角三角形，当△ABM 和 △ABC 相似时，一定有∠AMB=90° ，△BAM≌△ABC，即可得点 M 的坐标；（3）分矩形 DEFG 有两个顶 点 D、E 在 AB 上和矩形一个顶点在 AB 上两种情况求点的坐标. 试题解析： (1) 由题意：直线 1 22y x  与 x 轴交于点 B（4,0）， 与 y 轴交于点 C 点 C（0，-2）， 将点 B（4,0）代入抛物线 21 22y x bx   易得 3 2b   ∴所求抛物线解析式为： 21 3 22 2y x x   (2) ∵ 2 2 2AC BC AB  , ∴△ABC 为直角三角形，∠BCA=90° ∵点 M 是上述抛物线上一点∴不可能有 MB 与 AB 或者 MA 与 AB 垂直 当△ABM 和△ABC 相似时，一定有∠AMB=90° △BAM≌△ABC 此时点 M 的坐标为：M（3，-2） (3)∵△ABC 为直角三角形， ∠BCA=90° 当矩形 DEFG 只有顶点 D 在 AB 上时，显然点 F 与点 C 重合时面积最大，如图 1， 设 CG＝x， ∵DG∥BC，∴△AGD∽△ACB. ∴AG：AC＝DG∶BC，即 5 5 2 5 x DG  ∴DG＝2( －x) ∴S 矩形 DEFG＝－2(x－ ) 2 ＋ 即 x＝ 5 2 时矩形 DEFG 的面积有最大值 5 2 ， 当矩形 DEFG 有两个顶点 D、E 在 AB 上时，如图 2， CO 交 GF 于点 H，设 DG＝x，则 OH＝x，CH＝2－x，∵GF∥AB，∴△CGF∽△CAB， ∴GF∶AB＝CH∶CO，即 GF∶5＝(2－x)∶2，解得 GF＝ (2－x)． ∴S 矩形 DEFG＝x· (2－x)＝－ (x－1)2＋ ，即当 x＝1 时矩形 DEFG 的面积同样有最大值 5 2 ， 综上所述，无论矩形 DEFG 有两个顶点或只有一个顶点在 AB 上，其最大面积相同 当矩形一个顶点在 AB 上时， GD＝2( －x)＝ ，AG＝ ， ∴AD＝ ， OD＝AD－OA＝ ， ∴D( ，0)． 当矩形 DEFG 有两个顶点 D、E 在 AB 上时，∵DG＝1， ∴DE＝ 5 2 ， ∵DG∥OC，∴△ADG∽△AOC，∴AD∶AO＝DG∶OC，解得 AD＝ ， ∴OD＝ ， OE＝ － ＝2， ∴D(－ ，0)，E(2，0)． 综上所述，满足题意的矩形在 AB 边上的顶点的坐标为 D( ，0)或 D(－ ，0)、E(2，0) ． 点睛：此题考查了二次函数解析式的确定、直角三角形的判定、矩形面积的计算方法、二次函数最值的应 用等知识，要注意（3）题中，矩形的摆放方法有两种，不要漏解． 21．如图，抛物线 y= 1 2 x2+bx+c 与直线 y= 1 2 x+3 交于 A，B 两点，交 x 轴于 C、D 两点，连接 AC、BC， 已知 A（0，3），C（﹣3，0）． （1）求抛物线的解析式； （2）在抛物线对称轴 l 上找一点 M，使|MB﹣MD|的值最大，并求出这个最大值； （3）点 P 为 y 轴右侧抛物线上一动点，连接 PA，过点 P 作 PQ⊥PA 交 y 轴于点 Q，问：是否存在点 P 使 得以 A，P，Q 为顶点的三角形与△ABC 相似？若存在，请求出所有符合条件的点 P 的坐标；若不存在， 请说明理由． 【答案】（1）抛物线的解析式是 y= 1 2 x2+ 5 2 x+3；（2）|MB﹣MD|取最大值为 2 ；（3）存在点 P（1，6）． 【解析】 分析：（1）根据待定系数法，可得函数解析式； （2）根据对称性，可得 MC=MD，根据解方程组，可得 B 点坐标，根据两边之差小于第三边，可得 B，C， M 共线，根据勾股定理，可得答案； （3）根据等腰直角三角形的判定，可得∠BCE，∠ACO，根据相似三角形的判定与性质，可得关于 x 的方 程，根据解方程，可得 x，根据自变量与函数值的对应关系，可得答案． 详解：（1）将 A（0，3），C（﹣3，0）代入函数解析式，得 3 9 3 02 c b c     ，解得 5 2 3 b c     ， 抛物线的解析式是 y= 1 2 x2+ 5 2 x+3； （2）由抛物线的对称性可知，点 D 与点 C 关于对称轴对称， ∴对 l 上任意一点有 MD=MC， 联立方程组 2 1 32 1 5 32 2 y x y x x        ， 解得 0 3 x y    （不符合题意，舍）， 4 1 x y     ， ∴B（﹣4，1）， 当点 B，C，M 共线时，|MB﹣MD|取最大值，即为 BC 的长， 过点 B 作 BE⊥x 轴于点 E， ， 在 Rt△BEC 中，由勾股定理，得 BC= 2 2 2BE CE  ， |MB﹣MD|取最大值为 2 ； （3）存在点 P 使得以 A，P，Q 为顶点的三角形与△ABC 相似， 在 Rt△BEC 中，∵BE=CE=1， ∴∠BCE=45°， 在 Rt△ACO 中， ∵AO=CO=3， ∴∠ACO=45°， ∴∠ACB=180°﹣45°﹣45°=90°， 过点 P 作 PQ⊥y 轴于 Q 点，∠PQA=90°， 设 P 点坐标为（x， 1 2 x2+ 5 2 x+3）（x＞0） ①当∠PAQ=∠BAC 时，△PAQ∽△CAB， ∵∠PGA=∠ACB=90°，∠PAQ=∠CAB， ∴△PGA∽△BCA， ∴ BC AC PG AG  ，即 1 3 PG BC AD AC   ， ∴ 2 1 1 5 332 2 x x x    ， 解得 x1=1，x2=0（舍去）， ∴P 点的纵坐标为 1 2 ×12+ 5 2 ×1+3=6， ∴P（1，6）， ②当∠PAQ=∠ABC 时，△PAQ∽△CBA， ∵∠PGA=∠ACB=90°，∠PAQ=∠ABC， ∴△PGA∽△ACB， ∴ BC AC AG PG  ， 即 PG AC AG PG  =3， ∴ 2 31 5 3 32 2 x x x     ， 解得 x1=﹣13 3 （舍去），x2=0（舍去） ∴此时无符合条件的点 P， 综上所述，存在点 P（1，6）． 点睛：本题考查了二次函数综合题，解（1）的关键是利用待定系数法求函数解析式；解（2）的关键是利 用两边只差小于第三边得出 M，B，C 共线；解（3）的关键是利用相似三角形的判定与性质得出关于 x 的 方程，要分类讨论，以防遗漏． 22．如图，已知抛物线经过原点 O，顶点 A（1，﹣1），且与直线 y＝kx+2 相交于 B（2，0）和 C 两点 （1）求抛物线和直线 BC 的解析式； （2）求证：△ABC 是直角三角形； （3）抛物线上存在点 E（点 E 不与点 A 重合），使∠BCE＝∠ACB，求出点 E 的坐标； （4）在抛物线的对称轴上是否存在点 F，使△BDF 是等腰三角形？若存在，请直接写出点 F 的坐标． 【答案】（1）y＝x2﹣2x，y＝﹣x+2；（2）详见解析；（3）E（ 5 5 2 4 , ）；（4）符合条件的点 F 的坐标（1， 7 ） 或（1，﹣ 7 ）或（1，2+ 7 ）或（1，2﹣ 7 ）． 【解析】（1）将 B（2，0）代入设抛物线解析式 y＝a（x﹣1）2﹣1，求得 a，将 B（2，0）代入 y＝kx+2， 求得 k； （2）分别求出 AB2、BC2、AC2，根据勾股定理逆定理即可证明； （3）作∠BCE＝∠ACB，与抛物线交于点 E，延长 AB，与 CE 的延长线交于点 A'，过 A'作 A'H 垂直 x 轴于 点 H，设二次函数对称轴于 x 轴交于点 G．根据对称与三角形全等，求得 A'（3，1），然后求出 A'C 解析式， 与抛物线解析式联立，求得点 E 坐标； （4）设 F（1，m），分三种情况讨论：①当 BF＝BD 时， 21 2 2m  ，②当 DF＝BD 时， 2 4 5 2 2m m   ，③当 BF＝DF 时， 2 21 4 5m m m    ，m＝1，然后代入即可． 【详解】（1）设抛物线解析式 y＝a（x﹣1）2﹣1， 将 B（2，0）代入， 0＝a（2﹣1）2﹣1， ∴a＝1， 抛物线解析式：y＝（x﹣1）2﹣1＝x2﹣2x， 将 B（2，0）代入 y＝kx+2， 0＝2k+2， k＝﹣1， ∴直线 BC 的解析式：y＝﹣x+2； （2）联立 2 2 2 y x y x x       ， 解得 1 1 1 3 x y     ， 2 2 2 0 x y    ， ∴C（﹣1，3）， ∵A（1，﹣1），B（2，0）， ∴AB2＝（1﹣2）2+（﹣1﹣0）2＝2， AC2＝[1﹣（﹣1）]2+（﹣1﹣3）2＝20， BC2＝[2﹣（﹣1）]2+（0﹣3）2＝18， ∴AB2+BC2＝AC2， ∴△ABC 是直角三角形； （3）如图，作∠BCE＝∠ACB，与抛物线交于点 E，延长 AB，与 CE 的延长线交于点 A'，过 A'作 A'H 垂直 x 轴于点 H，设二次函数对称轴于 x 轴交于点 G． ∵∠BCE＝∠ACB，∠ABC＝90°， ∴点 A 与 A'关于直线 BC 对称， AB＝A'B， 可知△AFB≌△A'HB（AAS）， ∵A（1，﹣1），B（2，0） ∴AG＝1，BG＝OG＝1， ∴BH＝1，A'H＝1，OH＝3， ∴A'（3，1）， ∵C（﹣1，3）， ∴直线 A'C： 1 5 2 2y x   ， 联立： 2 1 5 2 2 2 y x y x x        ， 解得 1 3 x y     或 5 2 5 4 x y     ， ∴E（ 5 2 ， 5 4 ）； （4）∵抛物线的对称轴：直线 x＝1， ∴设 F（1，m）， 直线 BC 的解析式：y＝﹣x+2； ∴D（0，2） ∵B（2，0）， ∴BD＝ 1 2 x x 2 2 2(2 1) (0 ) 1BF m m      ， 2 2 2(1 0) ( 2) 4 5DF m m m       ， ①当 BF＝BD 时， 21 2 2m  ， m＝± 7 ， ∴F 坐标（1， 7 ）或（1，﹣ 7 ） ②当 DF＝BD 时， 2 4 5 2 2m m   ， m＝2± 7 ， ∴F 坐标（1，2+ 7 ）或（1，2﹣ 7 ） ③当 BF＝DF 时， 2 21 4 5m m m    ， m＝1， F（1，1），此时 B、D、F 在同一直线上，不符合题意． 综上，符合条件的点 F 的坐标（1， 7 ）或（1，﹣ 7 ）或（1，2+ 7 ）或（1，2﹣ 7 ）． 【点睛】考查了二次函数，熟练掌握二次函数的性质是解题的关键． 23．已知：如图，在平面直角坐标系 xOy 中，抛物线 y=ax2﹣4ax+1 与 x 轴的正半轴交于点 A 和点 B，与 y 轴交于点 C，且 OB=3OC，点 P 是第一象限内的点，连接 BC，△PBC 是以 BC 为斜边的等腰直角三角形． （1）求这个抛物线的表达式； （2）求点 P 的坐标； （3）点 Q 在 x 轴上，若以 Q、O、P 为顶点的三角形与以点 C、A、B 为顶点的三角形相似，求点 Q 的坐 标． 【答案】（1） 21 4 13 3y x x   ；（2）P（2，2）；（3）（﹣4，0）或（﹣2，0）． 【解析】 试题分析：（1）利用待定系数法即可得出结论； （2）先判断出△PMC≌△PNB，再用 PC2=PB2，建立方程求解即可； （3）先判断出点 Q 只能在点 O 左侧，再分两种情况讨论计算即可． 试题解析：（1）∵抛物线 y=ax2﹣4ax+1，∴点 C 的坐标为（0，1）． ∵OB=3OC，∴点 B 的坐标为（3，0），∴9a﹣12a+1=0，∴a= 1 3 ，∴ 21 4 13 3y x x   ． （2）如图，过点 P 作 PM⊥y 轴，PN⊥x 轴，垂足分别为点 M、N． ∵∠MPC=90°﹣∠CPN，∠NPB=90°﹣∠CPN，∴∠MPC=∠NPB． 在△PCM 和△PBN 中，∵∠PMC=∠PNB，∠MPC=∠NPB，PC=PB，∴△PMC≌△PNB，∴PM=PN． 设点 P（a，a）． ∵PC2=PB2，∴a2+（a﹣1）2=（a﹣3）2+a2． 解得 a=2，∴P（2，2）． （3）∵该抛物线对称轴为 x=2，B（3，0），∴A（1，0）． ∵P（2，2），A（1，0），B（3，0），C（0，1），∴PO= 2 2 ，AC= 2 2 ，AB=2． ∵∠CAB=135°，∠POB=45°，在 Rt△BOC 中，tan∠OBC= ，∴∠OBC≠45°，∠OCB＜90°，在 Rt△OAC 中，OC=OA，∴∠OCA=45°，∴∠ACB＜45°，∴当△OPQ 与△ABC 相似时，点 Q 只有在点 O 左侧时． （i）当 AC OQ AB OP  时，∴ 2 2 2 2 OQ ，∴OQ=4，∴Q（﹣4，0）． （ii）当 时，∴ ，∴OQ=2，∴Q（﹣2，0）． 当点 Q 在点 A 右侧时，综上所述，点 Q 的坐标为（﹣4，0）或（﹣2，0）． 考点：1．相似形综合题；2．分类讨论． 24．如图，已知抛物线 y＝ax2+bx﹣3 与 x 轴交于 A、B 两点，与 y 轴交于 C 点，经过 A、B、C 三点的圆的 圆心 M（1，m）恰好在此抛物线的对称轴上，⊙M 的半径为 5 ．设⊙M 与 y 轴交于 D，抛物线的顶点为 E． （1）求 m 的值及抛物线的解析式； （2）设∠DBC＝α，∠CBE＝β，求 sin（α﹣β）的值； （3）探究坐标轴上是否存在点 P，使得以 P、A、C 为顶点的三角形与△BCE 相似？若存在，请指出点 P 的位置，并直接写出点 P 的坐标；若不存在，请说明理由． 【答案】（1）m＝﹣1，y＝x2﹣2x﹣3；（2）sin（α﹣β）＝ 2 2 ；（3）在坐标轴上存在三个点 P1（0，0），P2 （0， 1 3 ），P3（9，0），使得以 P、A、C 为顶点的三角形与△BCE 相似． 【解析】（1）过 M 作 MN⊥y 轴于 N，连接 CM，利用勾股定理可知 m 的值，同样的方法可以求出点 B 的坐 标，将点 B 的坐标代入抛物线解析式中即可求. （2）通过计算可得出 OB OD BC CE  ，进而证明 Rt△BOD∽Rt△BCE，得∠CBE＝∠OBD＝β，则 sin（α﹣β） ＝sin（∠DBC﹣∠OBD）＝sin∠OBC 可求. （3）经过分析可知，根据题意分 Rt△COA∽Rt△BCE；过 A 作 AP2⊥AC 交 y 正半轴于 P2， Rt△CAP2∽Rt△BCE；过 C 作 CP3⊥AC 交 x 正半轴于 P3，Rt△P3CA∽Rt△BCE 三种情况，分情况讨论即可. 【详解】（1）由题意可知 C（0，﹣3）， 2 b a   1， ∴抛物线的解析式为 y＝ax2﹣2ax﹣3（a＞0）， 过 M 作 MN⊥y 轴于 N，连接 CM， 则 MN＝1，CM 5 ， 由勾股定理得 CN＝2，ON=1， ∴m＝﹣1． 同理可求得 B（3，0）， 将点 B 代入抛物线的解析式中得 ∴a×32﹣2a×3﹣3＝0，得 a＝1． ∴抛物线的解析式为 y＝x2﹣2x﹣3． （2）由（1）得 A（﹣1，0），E（1，﹣4），B（3，0），C（0，﹣3）． ∵M 到 AB，CD 的距离相等，OB＝OC， ∴OA＝OD， ∴点 D 的坐标为（0，1）， ∴在 Rt△BCO 中，BC 2 2OB OC   3 2 ， ∴ 3 31 OB OD   ， 在△BCE 中， ∵BC2+CE2＝ 2 2 2(3 2) [(1 0) ( 4 3) ] 18 2 20        2 2 2(3 1) (0 4) 20BE      2 2 2BC CE BE   ∴△BCE 是 Rt△ 3 2 3 2 BC CE   ， ∴ OB BC OD CE  ， 即 OB OD BC CE  ， ∴Rt△BOD∽Rt△BCE，得∠CBE＝∠OBD＝β， 因此 sin（α﹣β）＝sin（∠DBC﹣∠OBD）＝sin∠OBC 2 2 CO BC   ． （3）∵OB＝OC，OD＝OA， DOB AOC   DOB AOC   ∴Rt△COA∽Rt△BCE，此时点 P1（0，0）． 过 A 作 AP2⊥AC 交 y 正半轴于 P2， 则 Rt△CAP2∽Rt△BCE， 2CP AC BE BC   2 2(0 1) ( 3 0) 10AC       2 10 2 5 3 2 CP  2 10 3CP  2 2 10 133 3OP CP OC      ∴P2（0， 1 3 ）． 过 C 作 CP3⊥AC 交 x 正半轴于 P3， 则 Rt△P3CA∽Rt△BCE， 3AP AC BE CE   2 2(0 1) ( 3 4) 2CE       3 10 2 5 2 AP  2 10AP  3 2 10 1 9OP AP OA      ∴P3（9，0）． 故在坐标轴上存在三个点 P1（0，0），P2（0， 1 3 ），P3（9，0）， 使得以 P、A、C 为顶点的三角形与△BCE 相似． 【点睛】本题主要考查二次函数与圆、相似三角形的综合问题，掌握相似三角形的判定及性质是解题的关 键. 25．抛物线 2:F y x bx c   的图象经过坐标原点O ，且与 x 轴另交点为 3 ,03      . （1）求抛物线 F 的解析式； （2）如图1，直线  3: 03l y x m m   与抛物线 F 相交于点  1 1,A x y 和点  2 2,B x y （点 A 在第二象 限），求 2 1y y 的值（用含 m 的式子表示）； （3）在（2）中，若 4 3m  ，设点 A 是点 A 关于原点 O 的对称点，如图 2 .平面内是否存在点 P ，使得以点 A 、 B 、 A 、 P 为顶点的四边形是菱形？若存在，直接写出点 P 的坐标；若不存在，请说明理由. 【答案】（1）y=x2+ 3 3 x；（2）y2﹣y1== 2 33 m （m＞0）；（3）存在符合题意的点 P，且以点 A、B、A′、P 为顶点的菱形分三种情况，点 P 的坐标为（2 3 ， 2 3 ）、（﹣ 2 3 3 ，10 3 ）和（﹣ 2 3 3 ，﹣2）． 【解析】（1）根据点的坐标，利用待定系数法即可求出抛物线 F 的解析式； （2）将直线 l 的解析式代入抛物线 F 的解析式中，可求出 x1、x2 的值，利用一次函数图象上点的坐标特征 可求出 y1、y2 的值，做差后即可得出 y2-y1 的值； （3）根据 m 的值可得出点 A、B 的坐标，利用对称性求出点 A′的坐标．利用两点间的距离公式（勾股定理） 可求出 AB、AA′、A′B 的值，由三者相等即可得出△AA′B 为等边三角形；结合菱形的性质，可得出存在符合 题意得点 P，设点 P 的坐标为（x，y），分三种情况考虑：（i）当 A′B 为对角线时，根据菱形的性质（对角 线互相平分）可求出点 P 的坐标；（ii）当 AB 为对角线时，根据菱形的性质（对角线互相平分）可求出点 P 的坐标；（iii）当 AA′为对角线时，根据菱形的性质（对角线互相平分）可求出点 P 的坐标．综上即可得出 结论． 【详解】（1）∵抛物线 y=x2+bx+c 的图象经过点（0，0）和（- 3 3 ，0）， ∴ 1 3 03 3 0 b c c       ， 解得： 3 3 0 b c     ， ∴抛物线 F 的解析式为 y=x2+ 3 3 x． （2）将 y= 3 3 x+m 代入 y=x2+ 3 3 x，得：x2=m， 解得：x1=﹣ m ，x2= m ， ∴y1=﹣ 1 33 m +m，y2= 1 33 m +m， ∴y2﹣y1=（ 1 33 m +m）﹣（﹣ 1 33 m +m）= 2 33 m （m＞0）． （3）∵m= 4 3 ， ∴点 A 的坐标为（﹣ 2 3 3 ， 2 3 ），点 B 的坐标为（ 2 3 3 ，2）． ∵点 A′是点 A 关于原点 O 的对称点， ∴点 A′的坐标为（ 2 3 3 ，﹣ 2 3 ）． 由两点距离公式可得：AA′=AB=A′B= 8 3 ， ∴存在符合题意的点 P，且以点 A、B、A′、P 为顶点的菱形分三种情况，设点 P 的坐标为（x，y）． （i）当 A′B 为对角线时，有 2 3 2 3 23 3 2 3 x y       ， 解得： 2 3 2 3 x y    ， ∴点 P 的坐标为（2 3 ， 2 3 ）； （ii）当 AB 为对角线时，有 2 3 3 2 2 23 3 x y        ， 解得： 2 3 3 10 3 x y      ， ∴点 P 的坐标为（﹣ 2 3 3 ，10 3 ）； （iii）当 AA′为对角线时，有 2 3 3 2 22 3 3 x y        ， 解得： 2 3 3 2 x y       ， ∴点 P 的坐标为（﹣ 2 3 3 ，﹣2）． 【点睛】本题考查了待定系数法求二次函数解析式、一次函数图象上点的坐标特征、等边三角形的判定与 性质以及菱形的判定与性质，解题的关键是：（1）根据点的坐标，利用待定系数法求出二次函数解析式；（2） 将一次函数解析式代入二次函数解析式中求出 x1、x2 的值；（3）利用勾股定理（两点间的距离公式）求出 AB、AA′、A′B 的值；可知存在符合题意的点 P，且以点 A、B、A′、P 为顶点的菱形有三种情况，分 A′B 为 对角线、AB 为对角线及 AA′为对角线三种情况求出点 P 的坐标． 26．已知：如图，抛物线 y= 3 4 x2+bx+c 与 x 轴交于 A(-1，0)、B 两点（A 在 B 左），y 轴交于点 C（0，-3）． （1）求抛物线的解析式； （2）若点 D 是线段 BC 下方抛物线上的动点，求四边形 ABCD 面积的最大值； （3）若点 E 在 x 轴上，点 P 在抛物线上．是否存在以 B、C、E、P 为顶点且以 BC 为一边的平行四边形？ 若存在，求出点 P 的坐标；若不存在，请说明理由． 【答案】（1） 23 9 34 4y x x   ；（2） 27 2 ；（3）P1（3，-3），P2（ 3 41 2  ，3），P3（ 3 41 2  ，3）. 【解析】 试题分析：（1）将 ,A C 的坐标代入抛物线中，求出待定系数的值，即可得出抛物线的解析式． （2）根据 ,B C 的坐标，易求得直线 BC 的解析式．由于 AB OC、 都是定值，则 ABC△ 的面积不变，若 四边形 ABCD 面积最大，则 BDC 的面积最大；过点 D 作 DM y 轴交 BC 于 M ，则 3, 34M x x    ，可 得到当 BDC 面积有最大值时，四边形 ABCD 的面积最大值. （3）本题应分情况讨论：①过C 作 x 轴的平行线，与抛物线的交点符合 P 点的要求，此时 ,P C 的纵坐标相 同，代入抛物线的解析式中即可求出 P 点坐标；②将 BC 平移，令C 点落在 x 轴（即 E 点）、 B 点落在抛物 线（即 P 点）上；可根据平行四边形的性质，得出 P 点纵坐标（ ,P C 纵坐标的绝对值相等），代入抛物线的 解析式中即可求得 P 点坐标． 试题解析：（1）把  ( 10)  0 3A C， ，  代入 23 4y x bx c   ， 可以求得 9 34b c   ， ∴ 23 9 3.4 4y x x   （2）过点 D 作 DM y 轴分别交线段 BC 和 x 轴于点 M N、 ， 在 23 9 3.4 4y x x   中，令 0y  ，得 1 24 1.x x，    4 0 .B ， 设直线 BC 的解析式为 ,y kx b  可求得直线 BC 的解析式为： 3 3.4y x  ∵S 四边形 ABCD  1 1 155 3 4 0 2 .2 2 2ABC ADCS S DM DM            设 23 9, 3 ,4 4D x x x     3, 3 .4M x x    2 23 3 9 33 3 3 .4 4 4 4DM x x x x x           当 2x  时， DM有最大值3. 此时四边形 ABCD 面积有最大值 27 .2 （3）如图所示，  1 2 3 3 41 3 413 3 , 3 , 3 .2 2P P P， ， ，               27．如图，在平面直角坐标系中有抛物线 y＝a（x﹣2）2﹣2 和 y＝a（x﹣h）2，抛物线 y＝a（x﹣2）2﹣2 经过原点，与 x 轴正半轴交于点 A，与其对称轴交于点 B；点 P 是抛物线 y＝a（x﹣2）2﹣2 上一动点，且 点 P 在 x 轴下方，过点 P 作 x 轴的垂线交抛物线 y＝a（x﹣h）2 于点 D，过点 D 作 PD 的垂线交抛物线 y ＝a（x﹣h）2 于点 D′（不与点 D 重合），连接 PD′，设点 P 的横坐标为 m： （1）①直接写出 a 的值； ②直接写出抛物线 y＝a（x﹣2）2﹣2 的函数表达式的一般式； （2）当抛物线 y＝a（x﹣h）2 经过原点时，设△PDD′与△OAB 重叠部分图形周长为 L： ①求 PD DD 的值； ②直接写出 L 与 m 之间的函数关系式； （3）当 h 为何值时，存在点 P，使以点 O、A、D、D′为顶点的四边形是菱形？直接写出 h 的值． 【答案】（1）① 1 2 ；②y＝ 21 2 x ﹣2x； （2）①1； ②L＝ 2 (2 2) (0 2) 2 1 (2 2 1) 4 (2 4)2 m m m m          „ ； （3）h＝± 2 3 ． 【解析】（1）①将 x＝0，y＝0 代入 y＝a（x﹣2）2﹣2 中计算即可；②y＝ 21 2 x ﹣2x； （2）将（0，0）代入 y＝a（x﹣h）2 中，可求得 a＝ 1 2 ，y＝ 1 2 x2，待定系数法求 OB、AB 的解析式，由点 P 的横坐标为 m，即可表示出相应线段求解； （3）以点 O、A、D、D′为顶点的四边形是菱形，DD′＝OA，可知点 D 的纵坐标为 2，再由 AD＝OA＝4 即 可求出 h 的值． 【详解】解：（1）①将 x＝0，y＝0 代入 y＝a（x﹣2）2﹣2 中， 得：0＝a（0﹣2）2﹣2， 解得：a＝ 1 2 ； ②y＝ 21 2 x ﹣2x；． （2）∵抛物线 y＝a（x﹣h）2 经过原点，a＝ 1 2 ； ∴y＝ 1 2 x2， ∴A（4，0），B（2，﹣2）， 易得：直线 OB 解析式为：y＝﹣x，直线 AB 解析式为：y＝x﹣4 如图 1， 2 2 21 1 1, 2 , , , ( ,0), ( , ), ,2 2 2P m m m D m m E m F m m D m m                  ， ① 2 21 1 2 2 , 22 2PD m m m m DD m        PD 2m 1DD 2m   ②如图 1，当 0＜m≤2 时，L＝OE+EF+OF＝ 2 (2 2)m m m m    ， 当 2＜m＜4 时，如图 2，设 PD′交 x 轴于 G，交 AB 于 H，PD 交 x 轴于 E，交 AB 于 F， 则 2 2 21 1 1, 2 , , , ( ,0), ( , 4), ,2 2 2P m m m D m m E m F m m D m m                  ， 2 21 1( 4) 2 3 42 2PF m m m m m           ， 2 22 2 3 2 2m m 2 2,PG m 2 2m2 4 2 2FH PH PF         ∵DD′∥EG EG PE DD PD  ，即：EG•PD＝PE•DD′，得：EG•（2m）＝（2m﹣ 1 2 m2）•2m ∴EG＝2m﹣ 1 2 m2，EF＝4﹣m ∴L＝EG+EF+FH+GH＝EG+EF+PG 2 21 22 4 2 22 2m m m m m            22 1m (2 2 1)m 42      2 (2 2)m(0 m 2) 2 1m (2 2 1)m 4 (2 m 4)2 L            „ ； （3）如图 3， ∵OADD′为菱形 ∴AD＝AO＝DD′＝4， ∴PD＝2， 2 3PA  2 3h   【点睛】本题是二次函数综合题，考查了待定系数法求函数解析式，菱形的性质，抛物线的平移等，解题 时要注意考虑分段函数表示方法． 28．综合与探究 如图，抛物线 与 轴交于 、 两点，与 轴交于点 . （1）求抛物线解析式： （2）抛物线对称轴上存在一点 ，连接 、 ，当 值最大时，求点 H 坐标： （3）若抛物线上存在一点 ， ，当 时，求点 坐标： （4）若点 M 是 平分线上的一点，点 是平面内一点，若以 、 、 、 为顶点的四边形是矩形，请 直接写出点 坐标. 【答案】（1） ；（2）点 ；（3） ；（4） ， 【解析】（1）把 A、B 两点坐标代入抛物线解析式，解方程组求出 a、b 的值即可得答案；（2）连接 AC， 延长 AC 交抛物线对称轴与 H，由 A、C 两点坐标可得直线 AC 的解析式，根据抛物线解析式可得对称轴方 程，根据 A、C、H 三点在一条直线时， 的值最大，即可得答案；（3）由 C 点坐标可得△ABC 和 △ABP 的高为 4，可得 P 点纵坐标 n=±4，把 n=±4 代入抛物线解析式求出 m 的值，根据 mn>0 即可得 P 点 坐标；（4）设∠BAC 的角平分线与 y 轴交于 E 点，过点 E 作 EF⊥AC，根据角平分线的性质可证明 △AFE≌△AOE，可得出 AF 的长，利用勾股定理可求出 OE 的长，可得 E 点坐标，进而利用待定系数法可 求出直线 AE 的解析式，分两种情况：①当∠ABM1=90°时，M1N1=AB，AN1=BM，M1B⊥x 轴，可得点 M1 的横坐标，代入 AE 的解析式可得点 M1 的纵坐标，即可得出 BM 的长，进而可得 N1 点坐标；②当∠AM2B=90° 时，可知∠N2BA=∠BAE，过 N2 作 N2G⊥x 轴，根据点 E 坐标可得∠BAE 的正弦值和余弦值，即可求出 BN2 的长，利用∠N2BA 的正弦和余弦可求出 N2G 和 BG 的长，进而可得 OG 的长，即可得 N2 坐标；综上 即可得答案. 【详解】（1）∵A（-3，0），B（4，0），点 A、B 在抛物线上， ∴ 解得： ， ∴抛物线的解析式为：y= x2- x-4. （2）连接 AC，延长 AC 交抛物线对称轴与 H， ∵抛物线解析式为 y= x2- x-4，与 轴交于点 C ∴C（0，-4），对称轴为直线 x=- = ， ∵ ≤AC， ∴A、C、H 在一条直线上时 取最小值， 设直线 AC 的解析式为 y=kx+b, ∴ ， 解得： ， ∴直线 AC 的解析式为 y= x-4， 当 x= 时，y= ， ∴H 点坐标为（ ， ）. （3）∵S△ABC=S△ABP， ∴ AB OC= AB ， ∴ =4， 当 n=4 时，4= m2- m-4， 解得 m= ， ∵mn>0， ∴m= ， ∴P 点坐标为（ ，4） 当 n=-4 时，-4= m2- m-4， 解得：m=1 或 m=0， ∵mn>0， ∴m=1 或 m=0 均不符合题意， 综上：P 点坐标为（ ，4）. （4）设∠BAC 的角平分线交 y 轴于 E，过 E 作 EF⊥AC 于 F， ∵A（-3，0），B（4，0），C（0，-4）， ∴AB=7，AC=5，OA=3，OC=4， ∵AE 为∠BAC 的角平分线， ∴OE=EF， 又∵AE=AE， △AOE≌△FAE， ∴AF=OA=3， ∴FC=5-3=2， ∴EF2+FC2=CE2，即 OE2+22=(4-OE)2， 解得：OE= ， ∵点 E 在 y 轴负半轴， ∴E 点坐标为（0，- ）， 设直线 AE 的解析式为 y=kx+b， ∴ 解得： ∴直线 AE 的解析式为 y= ， ①当∠ABM1=90°时， ∵ANMB 是矩形， ∴M1N1=AB=7，AN1=BM，M1B⊥x 轴，AN1⊥x 轴， ∴x=4 时，y= ， ∴点 N1 坐标为（-3， ）. ②当∠AM2B=90°时，过 N2 作 N2G⊥x 轴， ∵AM2BN2 是矩形， ∴∠N2BA=∠BAE， ∵OA=3，OE= ， ∴AE= ， ∴sin∠BAE= = ，cos∠BAE= = ， ∴sin∠N2BA = ，cos∠N2BA= ∴BN2=AB cos∠N2BA= ， ∴N2G=BN2 sin∠N2BA= ，BG=BN2 cos∠N2BA= ， ∴OB-BG=- ， ∴点 N2 坐标为（- ， ）. 综上所述：点 N 的坐标为 N1（-3， ），N2（- ， ）. 【点睛】本题是二次函数的综合题型，其中涉及到的知识点有运用待定系数法求抛物线的解析式，二次函 数的性质，勾股定理，矩形的性质，三角函数的应用，综合性较强，注意分类思想的运用是解题关键. 29．如图，已知抛物线 y=ax2+bx+c（a≠0）的对称轴是 3 2x   ，且经过 A（﹣4，0），C（0，2）两点，直 线 l：y=kx+t（k≠0）经过 A，C． （1）求抛物线和直线 l 的解析式； （2）点 P 是直线 AC 上方的抛物线上一个动点，过点 P 作 PD⊥x 轴于点 D，交 AC 于点 E，过点 P 作 PF⊥AC， 垂足为 F，当△PEF≌△AED 时，求出点 P 的坐标； （3）在抛物线的对称轴上是否存在点 Q，使△ACQ 为等腰三角形？若存在，直接写出所有满足条件的 Q 点的坐标；若不存在，请说明理由． 【答案】（1） 21 3 22 2y x x    ， 1 22y x  ；（2） 3 5 15, 2P      ；（3）存在，Q 的坐标为： 3 55,2 2      或 3 55,2 2       3 55,2 2       或 3 71,22 2       或 3 71,22 2       或 3,02     ． 【解析】（1）把点 A、C 的坐标和对称轴表达式代入二次函数表达式，即可求解； （2）PE 1 2   n2 3 2  n+2 1 2  n﹣2，DE 1 2  n+2，sin∠EAD=sin∠CAO， 2 2 5 DE OC AE AC   ，则 AE 5 DE 5 （ 1 2 n+2），当△PEF≌△AED 时，PE=AE， 1 2  n2﹣2n 5 （ 1 2 n+2），即可求解； （3）等腰三角形分 A 为顶角顶点、以 C 为顶角顶点、点 Q 为顶角顶点，三种情况分别求解即可． 【详解】（1）把点 A、C 的坐标和对称轴表达式代入二次函数表达式得： 16 4 0 3 2 2 2 a b c b a c         ，解得： 1 2 3 2 2 a b c          ， 故抛物线的表达式为：y 1 2   x2 3 2  x+2； 同理把点 A、C 坐标代入直线 l 表达式并解得：y 1 2  x+2； （2）设 P 点坐标为（n， 1 2  n2 3 2  n+2），∴E 点坐标为（n， 1 2 n+2），∴PE 1 2   n2 3 2  n+2 1 2  n﹣2， DE 1 2  n+2． ∵A（﹣4，0），C（0，2），OA=4，OC=2，AC=2 5 ． ∵PD⊥x 轴于点 D，∴∠ADE=90°，∴sin∠EAD=sin∠CAO， 2 2 5 DE OC AE AC   ，∴AE 5 DE 5 （ 1 2 n+2），当△PEF≌△AED 时，PE=AE， 1 2  n2﹣2n 5 （ 1 2 n+2），解得：n=﹣4 或 5 （舍去﹣4）， ∴n= 5 ，∴P（ 5 ， 3 5 1 2  ）； （3）存在，理由如下： ①以 A 为顶角顶点，AQ=AC，由（2）知 AC=2 5 ，若设对称轴与 x 轴交于点 G，则 AG 3 2   （﹣4） 5 2  ； GQ1=GQ2 2 25 55(2 5) ( )2 2    ，故点 Q1、Q2 的坐标分别为（ 3 2  ， 55 2 ）、（ 3 2  ， 55 2  ）； ②以 C 为顶角顶点，CQ=CA=2 5 ，过点 C 作 x 轴的平行线，交抛物线的对称轴于点 M，则 M（ 3 2  ，2）， 则 CM 3 2  ，MQ3 2 23 71(2 5) ( )2 2    ，Q3G=2 71 2  ，Q4G=﹣2 71 2  ，故 Q3、Q4 坐标分别为（ 3 2  ， 2 71 2  ）、（ 3 2  ，2 71 2  ）； ③以点 Q 为顶角顶点时，同理可得点 Q5（ 3 2  ，0）； 故点 Q 的坐标为：（ 3 2  ， 55 2 ）或（ 3 2  ， 55 2  ）或（ 3 2  ，2 71 2  ）或（ 3 2  ，2 71 2  ）或（ 3 2  ， 0）． 【点睛】本题为二次函数综合运用题，涉及到一次函数、等腰三角形性质、三角形全等和相似等知识点， 其中（3），要注意分类求解，避免遗漏． 30．如图，在平面直角坐标系 xOy 中，O 为原点， ABCD 的边 AB 在 x 轴上，点 D 在 y 轴上，点 A 的坐 标为 ( 2,0) ， 6AB  ， 60BAD  ，点 E 是 BC 边上一点， DE BC ， P 过 A 、O 、 D 三点，抛物 线 2y ax bx c   过点 A 、 B 、 D 三点. (1)求抛物线的解析式. (2)若将 CDE 绕点 D 顺时针旋转 90 ，点 E 的对应点 E 会落在抛物线 2y ax bx c   上吗？请说明理由. (3)若点 M 为此抛物线的顶点，平面上是否存在点 N ，使得以点 B 、 D 、 M 、 N 为顶点的四边形为平行 四边形？若存在，请直接写出点 N 的坐标；若不存在，请说明理由. 【答案】（1） 23 3 2 34 2y x x    ；（2）点 E 的对应点 E'不在抛物线上,理由见详解；（3）N1 33 4 （ ， ） 或 N2 35 4       ， 或 N3 17 33 4      ， . 【解析】（1）先确定出点 B 的坐标，进而求出点 D 的坐标，最后用待定系数法求出抛物线解析式； （2）先利用旋转求出点 E'的坐标，最后判定点 E'是否在抛物线上； （3）分三种情况，利用线段的中点坐标公式，和平行四边形的对角线互相平分建立方程求解即可得出结论． 【详解】解：（1）∵A（-2，0），AB=6， ∴B（4，0）， ∴OB=4， ∵DO⊥AB，∠BAD=60°， ∴ 60 2 3OD OA tan   ， ∴D 0 2 3， ， ∵抛物线 2y ax bx c   过点 A，B，D； ∴ 4 2 0 16 4 0 2 3 a b c a b c c           解之得： 3 4 3 2 2 3 a b c           ， ∴抛物线的解析式为： 23 3 2 34 2y x x    ， （2）点 E 的对应点 E'不在抛物线上，理由：如图 1， ∵∠ADE=90°， ∴点 E'落在 DA 的延长线上，点 C'落在 y 轴上， ∴C'（0，-6）， 由旋转知，∠DC'E'=∠C=60°，C'E'=CE=3， 过点 E'作 E'H⊥DC'于 H， ∴ 3 3' ' ' 60 2E H C E sin   ， ' ' 0 2' 6 3C H C E cos   ， ∴ ' ' 2 39 2OH DC C H OD     ， ∵点 E'落在第三象限， ∴E' 9 2 3 3 2 32       ， ， 当 3 3 2x   ，代入抛物线： 23 3 2 34 2y x x    有： 2 3 3 3 3 3 3 5 3 9 92 3 2 34 2 2 2 16 4 4y                         ∴点 E'不在抛物线上； （3 如图，抛物线的解析式为： 23 3 2 34 2y x x    ∴M 9 31 4 （ ， ）， ∵B（4，0），D 0 2 3， ， 设 N（m，n）， ∵以点 B、D、M、N 为顶点的四边形为平行四边形， ①当 BD 与 MN 是对角线时， ∴   41 2 211 m    ， 9 3 2 31 2 4 1 2n         ∴m=3， 3 4n   ， ∴N1 33 4 （ ， ）， ②当 BM 与 DN 是对角线时，同①的方法得，N2 35 4       ， ③当 BN 与 DM 是对角线时，同①的方法得，N3 17 33 4      ， . 【点睛】此题是二次函数综合题，主要考查了待定系数法，相似三角形的判断和性质，平行四边形的性质， 直角三角形的性质，旋转的旋转，解（1）的关键是求出点 D 的坐标，解（2）的关键是利用旋转确定出点 E'的坐标，解（3 的关键是分类讨论的思想解决问题． 31．在平面直角坐标系 xOy 中，如图，抛物线 2 2y mx x n   （ m 、n 是常数）经过点 ( 2,3)A  、 ( 3,0)B  ， 与 y 轴的交点为点C ． （1）求此抛物线的表达式； （2）点 D 为 y 轴上一点，如果直线 BD 和直线 BC 的夹角为 15º，求线段CD 的长度； （3）设点 P 为此抛物线的对称轴上的一个动点，当△ BPC 为直角三角形时，求点 P 的坐标． 【答案】（1）抛物线的表达式是 322  xxy ;(2) 3 3CD   或 333  ;(3) P ( 1, 2)  或 ( 1,4) 或 3 17( 1, )2  或 3 17( 1, )2  . 【解析】（1）将点 A 和点 B 坐标代入解析式求解可得； （2）先求出点 C 坐标，从而得出 OC=OB=3，∠CBO=45°，据此知∠DBO=30°或 60°，依据 DO=BO•tan∠DBO 求出得 DO＝ 3 或 3 3 ，从而得出答案； （3）设 P（-1，t），知 BC2=18，PB2=4+t2，PC2=t2-6t+10，再分点 B、点 C 和点 P 为直角顶点三种情况分别 求解可得． 【详解】（1）依题意得： 4 4 3 9 6 0 m n m n        ， 解得： 1 3 m n     ∴抛物线的表达式是 2 2 3y x x    （2）∵抛物线 2 2 3y x x    与 y 轴交点为点C ∴点C 的坐标是 0,3 ，又点 B 的坐标是 3,0 ∴ 3OC OB  45CBO   ∴ 30DBO   或 60 在直角△ BOD 中， tanDO BO DBO   ∴ 3DO  或3 3 ，∴ 3 3CD   或3 3 3 . （3）由抛物线 2 2 3y x x    得：对称轴是直线 1x   根据题意：设  1,P t ，又点C 的坐标是 0,3 ，点 B 的坐标是 3,0 ∴ 2 18BC  ，  22 2 21 3 4PB t t      ，    2 22 21 3 6 10PC t t t       ， ①若点 B 为直角顶点，则 2 2 2BC PB PC  即： 2 218 4 6 10t t t     解之得： 2t   ， ②若点C 为直角顶点，则 2 2 2BC PC PB  即： 2 218 6 10 4t t t     解之得： 4t  ， ③若点 P 为直角顶点，则 2 2 2PB PC BC  即： 2 24 6 10 18t t t     解之得： 1 3 17 2t  ， 2 3 17 2t  . 综上所述 P 的坐标为  1, 2  或  1,4 或 3 171, 2      或 3 171, 2      . 【点睛】本题是二次函数的综合题，解题的关键是掌握待定系数法求函数解析式、等腰三角形的性质、两 点间的距离公式及直角三角形的性质等知识点． 32．如图，抛物线 y＝ax2+bx﹣4 经过 A（﹣3，0），B（5，﹣4）两点，与 y 轴交于点 C，连接 AB，AC， BC． （1）求抛物线的表达式； （2）求△ABC 的面积； （3）抛物线的对称轴上是否存在点 M，使得△ABM 是直角三角形？若存在，求出点 M 的坐标；若不存在， 请说明理由． 【答案】（1）y＝ 1 6 x2﹣ 5 6 x﹣4；（2）10；（3）存在，M1（ 5 2 ，11），M2（ 5 2 ，﹣ 22 3 ），M3（ 5 2 ， 55 2 ﹣ 2），M4（ 5 2 ，﹣ 55 2 ﹣2）. 【解析】（1）将点 A，B 代入 y＝ax2+bx﹣4 即可求出抛物线解析式； （2）在抛物线 y＝ 1 6 x2﹣ 5 6 x﹣4 中，求出点 C 的坐标，推出 BC∥x 轴，即可由三角形的面积公式求出△ABC 的面积； （3）求出抛物线 y＝ 1 6 x2﹣ 5 6 x﹣4 的对称轴，然后设点 M（ 5 2 ，m），分别使∠AMB＝90°，∠ABM＝90°， ∠AMB＝90°三种情况进行讨论，由相似三角形和勾股定理即可求出点 M 的坐标． 【详解】解：（1）将点 A（﹣3，0），B（5，﹣4）代入 y＝ax2+bx﹣4， 得 9 3 4 0 25 5 4 4 a b a b         ， 解得， 1 6 5 6 a b      ， ∴抛物线的解析式为：y＝ 1 6 x2﹣ 5 6 x﹣4； （2）在抛物线 y＝ 1 6 x2﹣ 5 6 x﹣4 中， 当 x＝0 时，y＝﹣4， ∴C（0，﹣4）， ∵B（5，﹣4）， ∴BC∥x 轴， ∴S△ABC＝ 1 2 BC•OC ＝ 1 2 ×5×4 ＝10， ∴△ABC 的面积为 10； （3）存在，理由如下： 在抛物线 y＝ 1 6 x2﹣ 5 6 x﹣4 中， 对称轴为： 5 2 2 bx a    ， 设点 M（ 5 2 ，m）， ①如图 1， 当∠M1AB＝90°时， 设 x 轴与对称轴交于点 H，过点 B 作 BN⊥x 轴于点 N， 则 HM1＝m，AH＝11 2 ，AN＝8，BN＝4， ∵∠AM1H+∠M1AN＝90°，∠M1AN+∠BAN＝90°， ∴∠M1AH＝∠BAN， 又∵∠AHM1＝∠BNA＝90°， ∴△AHM1∽△BNA， ∴ 1HMAH BN NA  ， 即 11 2 4 8 m ， 解得，m＝11， ∴M1（ 5 2 ，11）； ②如图 2， 当∠ABM2＝90°时， 设 x 轴与对称轴交于点 H，BC 与对称轴交于点 N， 由抛物线的对称性可知，对称轴垂直平分 BC， ∴M2C＝M2B， ∴∠BM2N＝∠AM2N， 又∵∠AHM2＝∠BNM2＝90°， ∴△AHM2∽△BNM2， ∴ 2 2 HMAH BN NM  ， ∵HM2＝﹣m，AH＝11 2 ，BN＝ 5 2 ，M2N＝﹣4﹣m， ∴ 11 2 5 4 2 m m    ， 解得， 22 3m   ， ∴M2（ 5 2 ，﹣ 22 3 ）； ③如图 3， 当∠AMB＝90°时， 设 x 轴与对称轴交于点 H，BC 与对称轴交于点 N， 则 AM2+BM2＝AB2， ∵AM2＝AH2+MH2，BM2＝BN2+MN2， ∴AH2+MH2+BN2+MN2＝AB2， ∵HM＝﹣m，AH＝11 2 ，BN＝ 5 2 ，MN＝﹣4﹣m， 即   2 2 22 2 211 5 4 4 82 2m m                ， 解得，m1＝ 55 2 ﹣2，m2＝﹣ 55 2 ﹣2， ∴M3（ 5 2 ， 55 2 ﹣2），M4（ 5 2 ，﹣ 55 2 ﹣2）； 综上所述，存在点 M 的坐标，其坐标为 M1（ 5 2 ，11），M2（ 5 2 ，﹣ 22 3 ），M3（ 5 2 ， 55 2 ﹣2），M4（ 5 2 ， ﹣ 55 2 ﹣2）． 【点睛】本题考查了待定系数法求解析式，三角形的面积，直角三角形的存在性，相似三角形的判定与性 质等，解题关键是注意分类讨论思想在解题中的运用．