2020中考数学复习基础小卷速测十三特殊四边形相关的折叠问题 5页

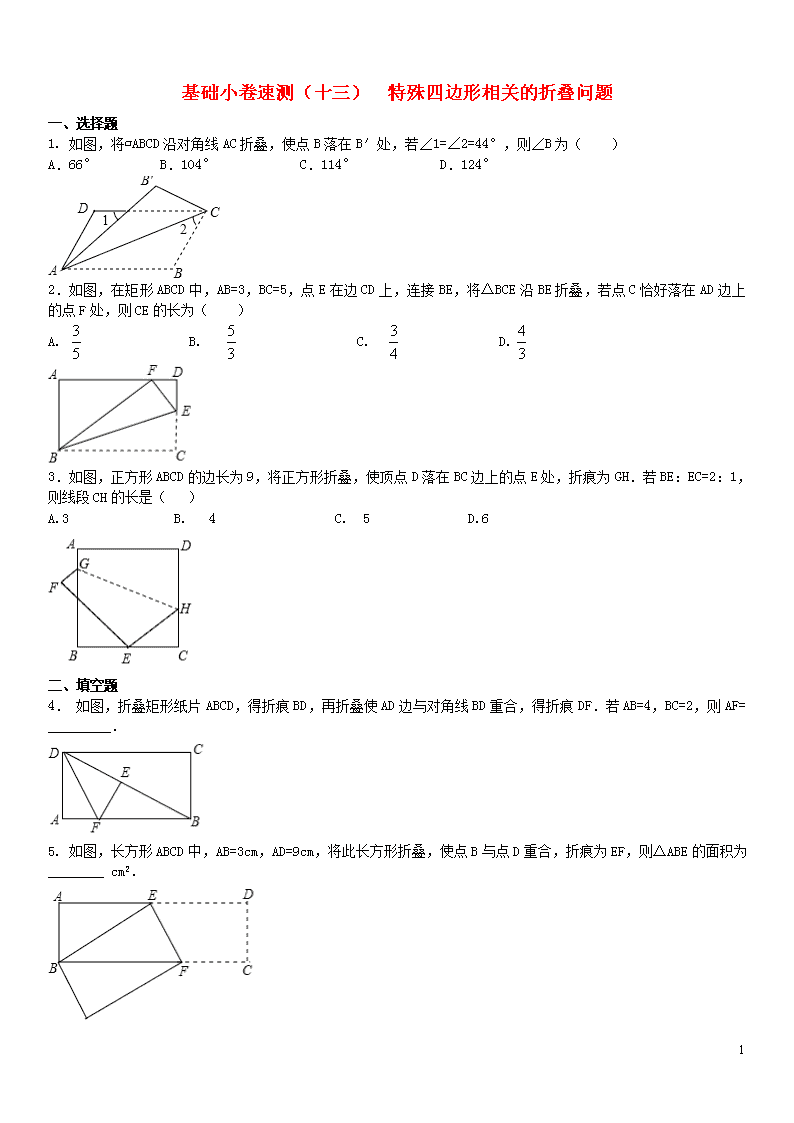
基础小卷速测（十三） 特殊四边形相关的折叠问题 一、选择题 ‎1. 如图，将▱ABCD沿对角线AC折叠，使点B落在B′处，若∠1=∠2=44°，则∠B为（　　）‎ A．66° B．104° C．114° D．124°‎ 2． 如图，在矩形ABCD中，AB=3，BC=5，点E在边CD上，连接BE，将△BCE沿BE折叠，若点C恰好落在AD边上的点F处，则CE的长为（　　）‎ A. ‎ B. C. D.‎ 3． 如图，正方形ABCD的边长为9，将正方形折叠，使顶点D落在BC边上的点E处，折痕为GH．若BE：EC=2：1，则线段CH的长是（ ）‎ A.3 B. 4 C. 5 D.6‎ 二、填空题 ‎4． 如图，折叠矩形纸片ABCD，得折痕BD，再折叠使AD边与对角线BD重合，得折痕DF．若AB=4，BC=2，则AF= _________．‎ ‎5. 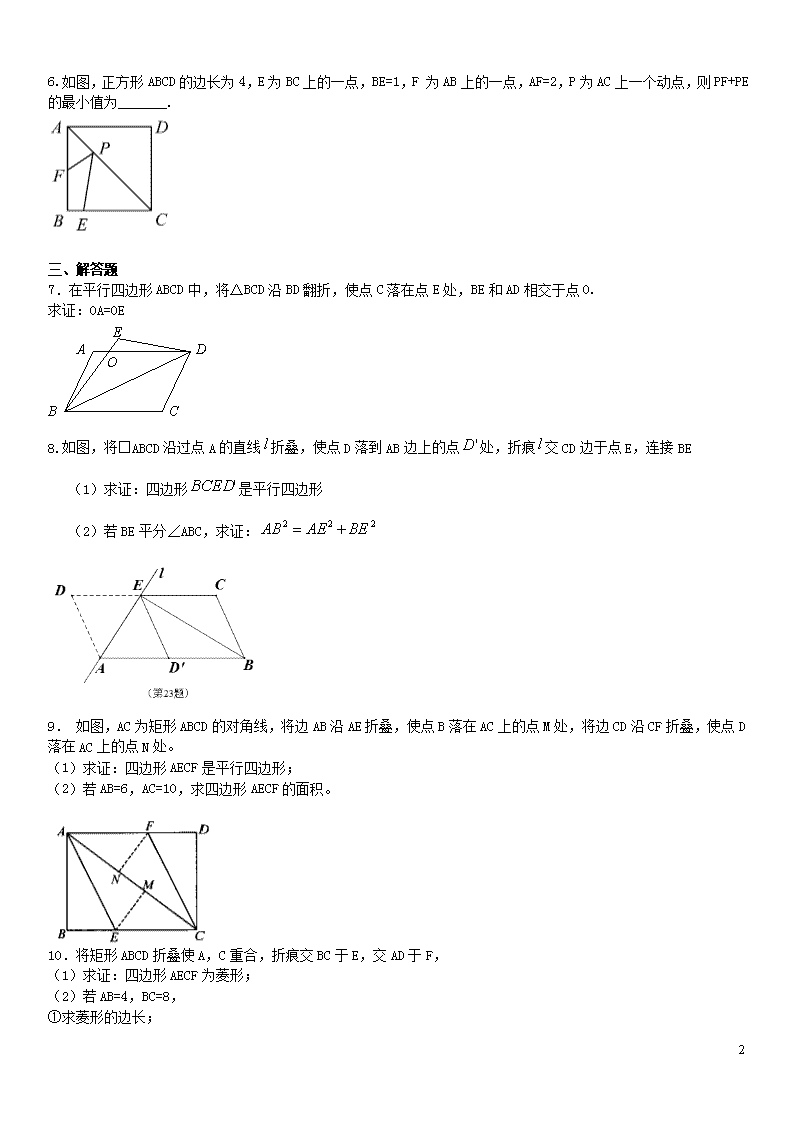如图，长方形ABCD中，AB=3cm，AD=9cm，将此长方形折叠，使点B与点D重合，折痕为EF，则△ABE的面积为________ cm2．‎ 5‎ ‎6.如图，正方形ABCD的边长为4，E为BC上的一点，BE=1，F 为AB上的一点，AF=2，P为AC上一个动点，则PF+PE的最小值为_______.‎ 三、解答题 ‎7．在平行四边形ABCD中，将△BCD沿BD翻折，使点C落在点E处，BE和AD相交于点O.‎ 求证：OA=OE A B C D E O ‎8.如图，将□ABCD沿过点A的直线折叠，使点D落到AB边上的点处，折痕交CD边于点E，连接BE ‎ （1）求证：四边形是平行四边形 ‎ （2）若BE平分∠ABC，求证：‎ ‎9． 如图，AC为矩形ABCD的对角线，将边AB沿AE折叠，使点B落在AC上的点M处，将边CD沿CF折叠，使点D落在AC上的点N处。‎ ‎（1）求证：四边形AECF是平行四边形；‎ ‎（2）若AB=6，AC=10，求四边形AECF的面积。‎ ‎10．将矩形ABCD折叠使A，C重合，折痕交BC于E，交AD于F， （1）求证：四边形AECF为菱形； （2）若AB=4，BC=8， ①求菱形的边长； ‎ 5‎ ‎②求折痕EF的长．‎ 参考答案 ‎1. C．【解析】∵四边形ABCD是平行四边形， ∴AB∥CD，∴∠ACD=∠BAC， 由折叠的性质得：∠BAC=∠B′AC，∴∠BAC=∠ACD=∠B′AC=∠1=22°， ∴∠B=180°-∠2-∠BAC=180°-44°-22°=114°. 2．B 【解析】设CE=x． ∵四边形ABCD是矩形， ∴AD=BC=5，CD=AB=3，∠A=∠D=90°． ∵将△BCE沿BE折叠，使点C恰好落在AD边上的点F处， ∴BF=BC=5，EF=CE=x，DE=CD-CE=3-x． 在Rt△ABF中，由勾股定理得： AF2=52-32=16， ∴AF=4，DF=5-4=1． 在Rt△DEF中，由勾股定理得： EF2=DE2+DF2， 即x2=（3-x）2+12， 解得x=． 3．B[解析]由题意设CH=xcm，则DH=EH=（9-x）cm， ∵BE：EC=2：1，∴CE=BC=3cm ∴在Rt△ECH中，EH2=EC2+CH2， 即（9-x）2=32+x2， 解得x=4，即CH=4cm． 4．-1 ‎ ‎5. 6【解析】∵将此长方形折叠，使点B与点D重合， ∴BE=ED． ∵AD=9cm=AE+DE=AE+BE． ∴BE=9-AE， 根据勾股定理可知：AB2+AE2=BE2． ∴32+AE2=（9-AE）2． 解得AE=4cm．∴△ABE的面积为×3×‎ 5‎ ‎4=6（cm2）． 6.【解析】作E关于直线AC的对称点E′，连接E′F，则E′F即为所求， 过F作FG⊥CD于G，‎ 在Rt△E′FG中，GE′=CD-BE-BF=4-1-2=1，GF=4，‎ ‎7．证明：∵四边形ABCD为平行四边形，∴AD∥BC，且AD=BC，∴∠ADB=∠CBD，由折叠可知∠EBD=∠CBD，BE=BC，∴∠EBD=∠ADB，∴BO=DO，∵AD= BE，∴AD - DO = BE- BO ，即OA=OE.‎ ‎8.证明：（1）∵将▱ABCD沿过点A的直线l折叠，使点D落到AB边上的点D′处， ∴∠DAE=∠D′AE，∠DEA=∠D′EA，∠D=∠AD′E， ∵DE∥AD′， ∴∠DEA=∠EAD′， ∴∠DAE=∠EAD′=∠DEA=∠D′EA， ∴∠DAD′=∠DED′， ∴四边形DAD′E是平行四边形， ∴DE=AD′， ∵四边形ABCD是平行四边形， ‎ ‎∴四边形BCED′是平行四边形； （2）∵BE平分∠ABC， ∴∠CBE=∠EBA， ∵AD∥BC， ∴∠DAB+∠CBA=180°， ∵∠DAE=∠BAE， ∴∠EAB+∠EBA=90°， ∴∠AEB=90°， ∴AB2=AE2+BE2．‎ ‎9．解：（1）证明：因为四边形ABCD是矩形，那么AD∥BC，AB∥CD，所以∠FAC=∠ACE，∠BAC=∠DCA。由折叠可得∠BAE=∠EAC=∠BAC，∠DCF=∠NCF=∠DCA，所以∠EAC=∠FCA。又因为AC=CA，所以△CAE△ACF，所以CE=AF。即四边形AECF是平行四边形。‎ ‎（2）因为AB=6，AC=10，由勾股定理，得BC=8.设EM=x，那么BE=EM=x，所以CE=BC-BE=8-x，CM=AC-AM=AC-AB=10-6=4.在Rt△‎ 5‎ CEM中，由勾股定理，得EM2+CM2=CE2，所以x2+42=(8-x)2，解得x=3。所以四边形AECF的面积=2△ACE的面积=2×AC×EM=30.‎ ‎10． 证明：（1）∵矩形ABCD折叠使A，C重合，折痕为EF， ∴OA=OC，EF⊥AC，EA=EC， ∵AD∥AC， ∴∠FAC=∠ECA，在△AOF和△COE中， ‎ ‎∴△AOF≌△COE， ∴OF=OE， ∵OA=OC，AC⊥EF， ∴四边形AECF为菱形； （2）①设菱形的边长为x，则BE=BC-CE=8-x，AE=x， 在Rt△ABE中，∵BE2+AB2=AE2， ∴（8-x）2+42=x2，解得x=5， 即菱形的边长为5； ②在Rt△ABC中，‎ ‎∴OA=AC=2， 在Rt△AOE中，AE=5， ‎ ‎∴EF=2OE=2．‎ 5‎