2012年初三数学房山一模试题 7页

房山区2012年九年级统一练习（一）‎ ‎ 　　　 数　学　 2012．4‎ 考生须知 ‎1．本试卷共6页，共五道大题，25个小题，满分120分．考试时间120分钟．‎ ‎2．在试卷和答题卡上认真填写学校名称、姓名和考试编号．‎ ‎3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效．‎ ‎4．考试结束，请将本试卷和答题卡一并交回．‎ 一、选择题（共8道小题，每小题4分，共32分）‎ 下列各题均有四个选项，其中只有一个是符合题意的．‎ ‎1．的相反数是（　　）．‎ A． B． C． D．‎ ‎2．神舟八号无人飞船，是中国“神舟”系列飞船的第八艘飞船，于‎2011年11月1日5时58分10秒由改进型“长征二号”F遥八火箭顺利发射升空。火箭全长约‎58.3米，起飞质量为497 000千克，将497 000用科学记数法表示为（ ）．‎ A．49.7×103 B．0.497×‎104 C．4.97×105 D．4.97×103 ‎ ‎3．在平面直角坐标系中，点P（－2，3）关于y轴对称的点的坐标为（ ）．‎ A．（2，－3） B．（－2，－3） C．（3，－2） D．（2，3）‎ ‎4．一个几何体的三视图如图所示，那么这个几何体的形状是（ ）．‎ 第3题图 ‎ ‎ ‎ A B C D ‎ ‎5．从1~30这连续30个正整数中，随机取出一个数，取出的数是5的倍数的概率是（ ）．‎ A． B． C． D．‎ ‎6．如果关于的一元二次方程有两个不相等的实数根，则的取值范围是（ ）．‎ A. B. 且 C. D. 且 ‎7. 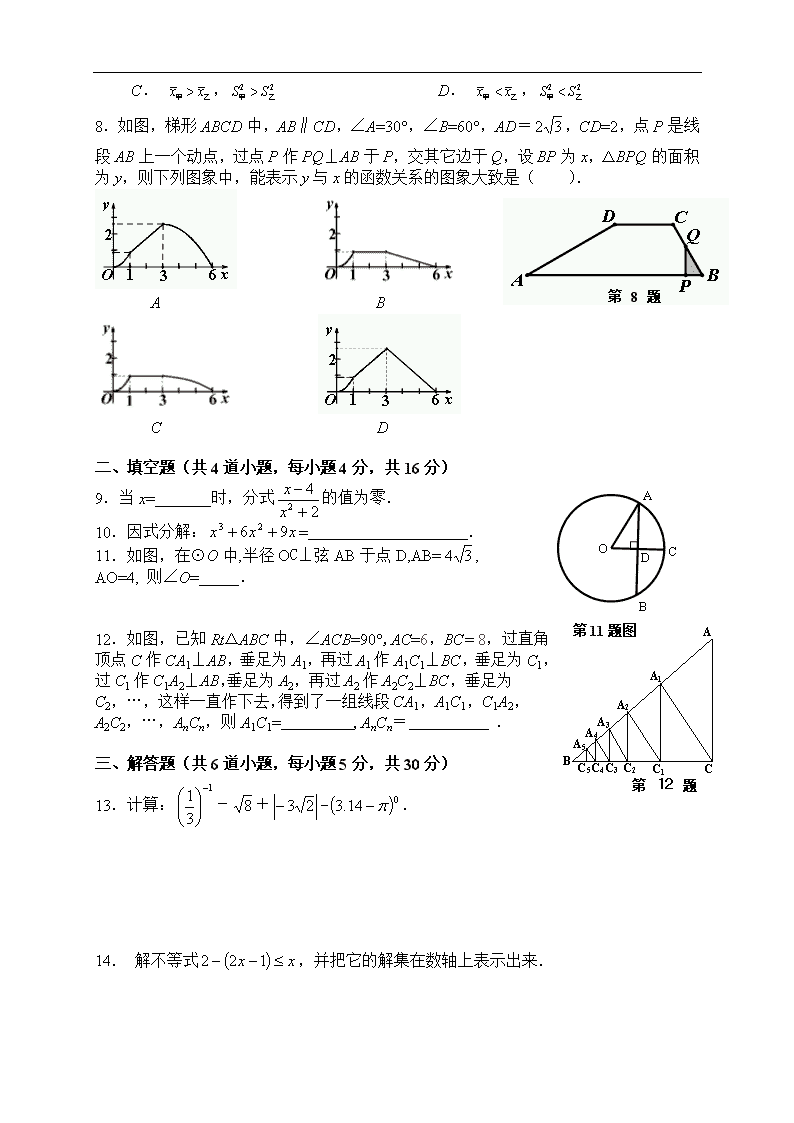甲、乙两个学习小组各有4名同学，在某次测验中，他们的得分如下表：‎ ‎ 得分 组别 ‎1号生得分 ‎2号生得分 ‎3号生得分 ‎4号生得分 甲组 ‎87分 ‎95分 ‎98分 ‎100分 乙组 ‎90分 ‎94分 ‎97分 ‎99分 设两组同学得分的平均数依次为，，得分的方差依次为，，则下列关系中完全正确的是（ ）．‎ A． ， B． ， ‎ C． ， D． ，‎ ‎8．如图，梯形ABCD中，AB∥CD，∠A=30°，∠B=60°，AD＝，CD=2，点P是线段AB上一个动点，过点P作PQ⊥AB于P，交其它边于Q，设BP为x，△BPQ的面积为y，则下列图象中，能表示y与x的函数关系的图象大致是（ ）．‎ 第8题图 ‎ ‎ ‎ A B ‎ ‎ ‎ C D ‎ 二、填空题（共4道小题，每小题4分，共16分）‎ 第11题图 ‎9．当x=_______时，分式的值为零．‎ ‎10．因式分解：= ．‎ ‎11．如图，在⊙O中,半径OC⊥弦AB于点D,AB=,‎ AO=4, 则∠O=_____．‎ 第12题图 ‎12．如图，已知Rt△ABC中，∠ACB=90°,AC=6，BC= 8，过直角顶点C作CA1⊥AB，垂足为A1，再过A1作A‎1C1⊥BC，垂足为C1，过C1作C‎1A2⊥AB，垂足为A2，再过A2作A‎2C2⊥BC，垂足为C2，…，这样一直作下去，得到了一组线段CA1，A‎1C1，C‎1A2，A‎2C2，…，AnCn，则A‎1C1= ,AnCn＝ ．‎ 三、解答题（共6道小题，每小题5分，共30分）‎ ‎13．计算：－＋-．‎ ‎14． 解不等式，并把它的解集在数轴上表示出来．‎ ‎15．已知：E是△ABC一边BA延长线上一点，且AE=BC ，过点A作AD∥BC，且使AD=AB，联结ED．‎ 求证：AC=DE．‎ ‎16．已知a2＋a=3，求代数式的值．‎ 解： ‎ ‎17．已知：反比例函数（）的图象与一次函数（）的图象交于点A(1，n)和点B(－2，－1)．‎ ‎⑴求反比例函数和一次函数解析式；‎ ‎⑵若一次函数的图象与x轴交于点C，P是x轴上的一点，当△ACP的面积为3时，求P点坐标．‎ 解：‎ ‎18．列方程或方程组解应用题：‎ 为响应低碳号召，肖老师上班的交通方式由自驾车改为骑自行车，肖老师家距学校‎15千米，因为自驾车的速度是骑自行车速度的4倍，所以肖老师每天比原来早出发45分钟，才能按原时间到校，求肖老师骑自行车每小时走多少千米．‎ 解：‎ 四、解答题（共4道小题，每小题均5分，共20分）‎ ‎19．如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，AD=DC，联结AC，过点D作DE⊥AC于点F，交BC于点G，交AB的延长线于点E，若AE=AC．‎ ‎⑴求∠EAC的度数 ‎⑵若AD=2，求AB的长．‎ 解：⑴‎ ‎⑵‎ ‎20．如图，在△ABC中，AB=BC，以AB为直径的⊙O与AC交于点D，过点D作DF⊥BC于点F，交AB的延长线于点E．‎ ‎⑴求证：直线DE是⊙O的切线；‎ ‎⑵当cosE=，BF=6时，求⊙O的直径．‎ ‎⑴证明：‎ ‎ ‎ ‎⑵解：‎ ‎21．母亲节快到了，某校团委随机抽取本校部分同学，进行母亲生日日期了解情况调查，分“知道、不知道、记不清”三种情况.下面图①、图②是根据采集到的数据，绘制的扇形和条形统计图.‎ 图②‎ ‎120°‎ 记不清 不知道 知道 图①‎ 请你根据图中提供的信息，解答下列问题：‎ ‎（1）在图①中，求出“不知道”部分所对应的圆心角的度数；‎ ‎（2）求本次被调查学生的人数，并补全条形统计图；‎ ‎（3）若全校共有1080名学生，请你估计这所学校有多少名学生知道母亲的生日？‎ ‎ ‎ ‎22．阅读下面材料：‎ 如图1，已知线段AB、CD相交于点O，且AB=CD，请你利用所学知识把线段AB、CD转移到同一三角形中．‎ 小强同学利用平移知识解决了此问题，具体做法：‎ 如图2，延长OD至点E，使DE=CO，延长OA至点F，使AF=OB，联结EF，则△OEF为所求的三角形．‎ 请你仔细体会小强的做法，探究并解答下列问题：‎ 如图3，长为2的三条线段AA′，BB′，CC′交于一点O，并且∠B′OA=∠C′OB=∠A′OC=60°；‎ ‎（1）请你把三条线段AA′，BB′，CC′ 转移到同一三角形中．‎ ‎（简要叙述画法）‎ ‎（2）联结AB′、BC′、CA′，如图4，设△AB′O、△BC′O、‎ ‎△CA′O的面积分别为S1、S2、S3，‎ 则S1+S2+S3 （填“>”或“<”或“=” ） ． ‎ 图2‎ 如图4‎ 图3‎ 五、解答题（共3道小题，23题7分，24题8分，25题7分，共22分）‎ ‎23． 已知：关于x的方程 ‎⑴求证：方程总有实数根；‎ ‎⑵若方程有一根大于5且小于7，求k的整数值；‎ ‎⑶在⑵的条件下，对于一次函数和二次函数=，当时，有，求b的取值范围．‎ 证明：⑴‎ 解：⑵‎ ‎⑶‎ ‎24．如图⑴，在平面直角坐标系中，O为坐标原点，抛物线y=ax2＋8ax＋‎16a＋6经过点B（0，4）.‎ ‎⑴求抛物线的解析式；‎ ‎⑵设抛物线的顶点为D，过点D、B作直线交x轴于点A，点C在抛物线的对称轴上，且C点的纵坐标为-4，联结BC、AC.求证：△ABC是等腰直角三角形；‎ ‎⑶在⑵的条件下，将直线DB沿y轴向下平移，平移后的直线记为l ，直线l 与x轴、y轴分别交于点A′、B′，是否存在直线l，使△A′B′C是直角三角形，若存在求出l 的解析式，若不存在，请说明理由．‎ ‎ ‎ ‎ 图⑴ 备用图 ‎ ‎ 解：⑴‎ 证明 ：⑵‎ ‎⑶‎ ‎25．如图1，在△ABC中，∠ACB=90°，AC=BC=，以点B为圆心，以为半径作圆. ‎ ‎⑴设点P为☉B上的一个动点，线段CP绕着点C顺时针旋转90°，得到线段CD，联结DA，DB，PB，如图2．求证：AD=BP；‎ ‎⑵在⑴的条件下，若∠CPB=135°，则BD=___________；‎ ‎⑶在⑴的条件下，当∠PBC=_______° 时，BD有最大值，且最大值为__________；‎ ‎ 当∠PBC=_________° 时，BD有最小值，且最小值为__________．‎