中考数学压轴题分类解析汇编大全+中考数学试题及答案等精品大全集 专题 6：由运动产生的线段和差问题 78页

中考数学压轴题分类解析 汇编大全+中考数学试题及答案等精品大全集 中考数学压轴题分类解析汇编 专题 6：由运动产生的线段和差问题 64.（2012 湖北恩施 8 分）如图，已知抛物线 y=﹣x2+bx+c 与一直线相交于 A（﹣1，0），C （2，3）两点，与 y 轴交于点 N．其顶点为 D．矚慫润厲钐瘗睞枥庑赖賃軔朧碍鳝绢。 （1）抛物线及直线 AC 的函数关系式； （2）设点 M（3，m），求使 MN+MD 的值最小时 m 的值； （3）若抛物线的对称轴与直线 AC 相交于点 B，E 为直线 AC 上的任意一点，过点 E 作 EF∥BD 交抛物线于点 F，以 B，D，E，F 为顶点的四边形能否为平行四边形？若能，求点 E 的坐标； 若不能，请说明理由；聞創沟燴鐺險爱氇谴净祸測樅锯鳗鲮。 （4）若 P 是抛物线上位于直线 AC 上方的一个动点，求△APC 的面积的最大值． 【答案】解：（1）由抛物线 y=﹣x2+bx+c 过点 A（﹣1，0）及 C（2，3）得， 1 b+c=0 4+2b+c=3    ，解得 b=2 c=3    。∴抛物线的函数关系式为 2y x 2x 3    。 设直线 AC 的函数关系式为 y=kx+n，由直线 AC 过点 A（﹣ 1，0）及 C（2，3）得 k+n=0 2k+n=3    ，解得 k=1 n=1    。 ∴直线 AC 的函数关系式为 y=x+1。 （2）作 N 点关于直线 x=3 的对称点 N′， 令 x=0，得 y=3，即 N（0，3）。 ∴N′（6， 3） 由  22y x 2x 3= x 1 +4      得 D（1，4）。 设直线 DN′的函数关系式为 y=sx+t，则 6s+t=3 s+t=4    ，解得 1s= 5 21t= 5     。 ∴故直线 DN′的函数关系式为 1 21y x5 5    。 根据轴对称的性质和三角形三边关系，知当 M（3，m）在直线 DN′上时，MN+MD 的值最小， ∴ 1 21 18m 3 =5 5 5     。 ∴使 MN+MD 的值最小时 m 的值为 18 5 。 （3）由（1）、（2）得 D（1，4），B（1，2）， ①当 BD 为平行四边形对角线时，由 B、C、D、N 的坐标知，四边形 BCDN 是平行四边形， 此时，点 E 与点 C 重合，即 E（2，3）。残骛楼諍锩瀨濟溆塹籟婭骒東戇鳖納。 ②当 BD 为平行四边形边时， ∵点 E 在直线 AC 上，∴设 E（x，x+1），则 F（x， 2x 2x 3   ）。 又∵BD=2 ∴若四边形 BDEF 或 BDFE 是平行四边形时，BD=EF。 ∴  2x 2x 3 x 1 =2     ，即 2x x 2 =2   。 若 2x x 2=2   ，解得，x=0 或 x=1（舍去），∴E（0，1）。 若 2x x 2= 2    ，解得， 1 17x= 2  ，∴E 1+ 17 3+ 17 2 2       ， 或 E 1 17 3 17 2 2       ， 。 综上，满足条件的点 E 为（2，3）、（0，1）、 1+ 17 3+ 17 2 2       ， 、 1 17 3 17 2 2       ， 。 （4）如图，过点 P 作 PQ⊥x 轴交 AC 于点 Q；过点 C 作 CG⊥x 轴于点 G， 设 Q（x，x+1），则 P（x，﹣x2+2x+3）。 ∴ 2 2PQ x 2x 3 x 1 x x 2         （ ）（ ） 。 ∴ APC APQ CPQ 1S S +S PQ AG2     2 21 3 1 27x x 2 3 x2 2 2 8         （ ） （ ） 。 ∵ 3 02 < ， ∴当 1x= 2 时，△APC 的面积取得最大值，最大值为 27 8 。 【考点】二次函数综合题，待定系数法，曲线上点的坐标与方程的关系，轴对称的性质，三 角形三边关系，平行四边形的判定和性质，二次函数的最值。酽锕极額閉镇桧猪訣锥顧荭钯詢鳕驄。 【分析】（1）利用待定系数法求二次函数解析式、一次函数解析式。 （2）根据轴对称的性质和三角形三边关系作 N 点关于直线 x=3 的对称点 N′，当 M（3，m） 在直线 DN′上时，MN+MD 的值最小。彈贸摄尔霁毙攬砖卤庑诒尔肤亿鳔简。 （3）分 BD 为平行四边形对角线和 BD 为平行四边形边两种情况讨论。 （4）如图，过点 P 作 PQ⊥x 轴交 AC 于点 Q；过点 C 作 CG⊥x 轴于点 G，设 Q（x，x+1）， 则 P （ x ， ﹣ x2+2x+3 ）， 求 得 线 段 PQ= ﹣ x2+x+2 。 由 图 示 以 及 三 角 形 的 面 积 公 式 知 APC APQ CPQS S +S   ，由二次函数的最值的求法可知△APC 的面积的最大值。謀荞抟箧飆鐸怼 类蒋薔點鉍杂篓鳐驱。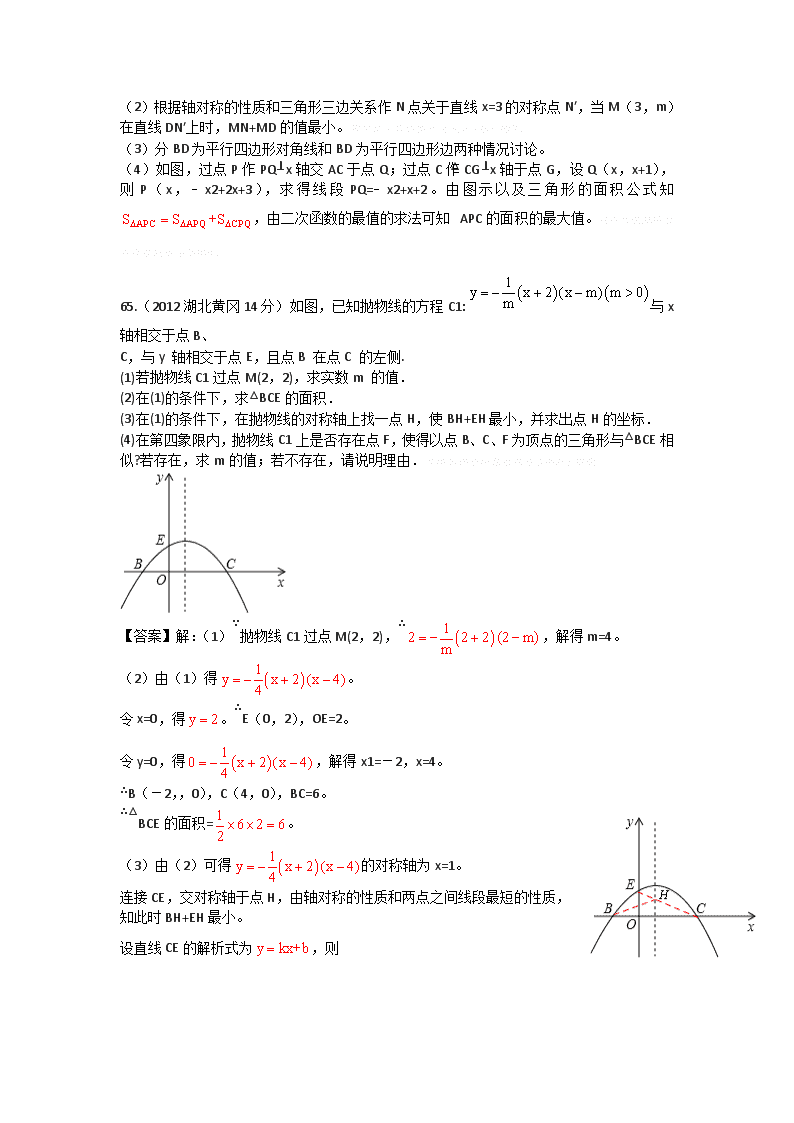 65.（2012 湖北黄冈 14 分）如图，已知抛物线的方程 C1:    1y x 2 (x m) m 0m      与 x 轴 相交于点 B、 C，与 y 轴相交于点 E，且点 B 在点 C 的左侧. (1)若抛物线 C1 过点 M(2，2)，求实数 m 的值． (2)在(1)的条件下，求△BCE 的面积． (3)在(1)的条件下，在抛物线的对称轴上找一点 H，使 BH+EH 最小，并求出点 H 的坐标． (4)在第四象限内，抛物线 C1 上是否存在点 F，使得以点 B、C、F 为顶点的三角形与△BCE 相似?若存在，求 m 的值；若不存在，请说明理由．厦礴恳蹒骈時盡继價骚卺癩龔长鳏檷。 【答案】解：（1）∵抛物线 C1 过点 M(2，2)，∴  12 2 2 (2 m)m     ，解得 m=4。 （2）由（1）得  1y x 2 (x 4)4     。 令 x=0，得 y 2 。∴E（0，2），OE=2。 令 y=0，得  10 x 2 (x 4)4     ，解得 x1=－2，x=4。 ∴B（－2，，0），C（4，0），BC=6。 ∴△BCE 的面积= 1 6 2 62    。 （3）由（2）可得  1y x 2 (x 4)4     的对称轴为 x=1。 连接 CE，交对称轴于点 H，由轴对称的性质和两点之间线段最短的性质， 知此时 BH+EH 最小。 设直线 CE 的解析式为 y kx+b ，则 4k+b=0 b=2    ，解得 1k= 2 b=2    。∴直线 CE 的解析式为 1y x+22   。 当 x=1 时， 3y 2  。∴H（1， 3 2 ）。 （4）存在。分两种情形讨论： ①当△BEC∽△BCF 时，如图所示。 则 BE BC BC BF  ，∴BC2=BE•BF。 由（2）知 B（－2，0），E（0，2），即 OB=OE， ∴∠EBC=45°，∴∠CBF=45°。 作 FT⊥x 轴于点 F，则 BT=TF。 ∴令 F（x，－x－2）（x＞0）， 又点 F 在抛物线上，∴－x－2=  1 x 2 (x m)m    ， ∵x+2＞0（∵x＞0），∴x=2m，F（2m，－2m－2）。 此时 2 2BF (2m 2) ( 2m 2) 2 2 m 1 BE 2 2 BC m 2         （ ）， ， ， 又 BC2=BE•BF，∴（m+2）2= 2 2 • 2 2 m 1（ ），解得 m=2± 2 2 。 ∵m＞0，∴m= 2 2 +2。 ②当△BEC∽△FCB 时，如图所示。 则 BC EC BF BC  ，∴BC2=EC•BF。 同①，∵∠EBC=∠CFB，△BTF∽△COE， ∴ TF OE 2 BT OC m   。 ∴令 F（x，－ 2 m （x+2））（x＞0）， 又点 F 在抛物线上，∴－ 2 m （x+2）=  1 x 2 (x m)m    。 ∵x+2＞0（∵x＞0）， ∴x=m+2。∴F（m+2，－ 2 m （m+4））， 2EC m 4  ，BC=m+2。 又 BC2=EC•BF，∴（m+2）2=    2 22 2 4 m+4m 4 m+2+2 + m   . 整理得：0=16，显然不成立。 综合①②得，在第四象限内，抛物线上存在点 F，使得以点 B、C、F 为顶点的三角形与△BCE 相似，m= 2 2 +2。茕桢广鳓鯡选块网羈泪镀齐鈞摟鳎饗。 【考点】二次函数综合题，曲线上点的坐标与方程的关系，二次函数的性质，轴对称的性质， 两点之间线段最短的性质，相似三角形的判定和性质。鹅娅尽損鹌惨歷茏鴛賴縈诘聾諦鳍皑。 【分析】（1）将点（2，2）的坐标代入抛物线解析式，即可求得 m 的值。 （2）求出 B、C、E 点的坐标，从而求得△BCE 的面积。 （3）根据轴对称以及两点之间线段最短的性质，可知点 B、C 关于对称轴 x=1 对称，连接 EC 与对称轴的交点即为所求的 H 点。籟丛妈羥为贍偾蛏练淨槠挞曉养鳌顿。 （4）分两种情况进行讨论： ①当△BEC∽△BCF 时，如图所示，此时可求得 2 2 +2。 ②当△BEC∽△FCB 时，如图所示，此时得到矛盾的等式，故此种情形不存在。 66.（2012 湖南郴州 10 分）如图，已知抛物线 2y ax bx c   经过 A（4，0），B（2，3），C （0，3）三点． （1）求抛物线的解析式及对称轴． （2）在抛物线的对称轴上找一点 M，使得 MA+MB 的值最小，并求出点 M 的坐标． （3）在抛物线上是否存在一点 P，使得以点 A、B、C、P 四点为顶点所构成的四边形为梯形？ 若存在，请求出点 P 的坐标；若不存在，请说明理由．預頌圣鉉儐歲龈讶骅籴買闥龅绌鳆現。 【答案】解：（1）∵抛物线 2y ax bx c   经过 A（4，0），B（2，3），C（0，3）三点， ∴ 16a 4b c 0 4a 2b c 3 c 3          ，解得 3a 8 3b 4 c 3         。 ∴抛物线的解析式为： 23 3y x x 38 4     ，其对称轴为： bx 12a    。 （2）由 B（2，3），C（0，3），且对称轴为 x=1，可知点 B、C 是关于对称 轴 x=1 的对称点。 如图 1 所示，连接 AC，交对称轴 x=1 于点 M，连接 MB，则 MA＋MB=MA ＋MC=AC，根据两点之间线段最短可知此时 MA＋MB 的值最小。渗釤呛俨 匀谔鱉调硯錦鋇絨钞陉鳅陸。 设直线 AC 的解析式为 y=kx＋b， ∵A（4，0），C（0，3），∴ 4k b 0 b 3     ，解得 3k 4 b 3      。 ∴直线 AC 的解析式为：y= 3 4  x＋3。 令 x=1，得 y= 9 4 。∴M 点坐标为（1， 9 4 ）。 （3）结论：存在。 如图 2 所示，在抛物线上有两个点 P 满足题意： ①若 BC∥AP1，此时梯形为 ABCP1。 由 B（2，3），C（0，3），可知 BC∥x 轴，则 x 轴与抛物线的另一个交点 P1 即为所求。 在 23 3y x x 38 4     中令 y=0，解得 x1=-2，x2=4。 ∴P1（－2，0）。 ∵P1A=6，BC=2，∴P1A≠BC。 ∴四边形 ABCP1 为梯形。 ②若 AB∥CP2，此时梯形为 ABCP2。 设 CP2 与 x 轴交于点 N， ∵BC∥x 轴，AB∥CP2，∴四边形 ABCN 为平行四边形。∴AN=BC=2。∴N（2，0）。 设直线 CN 的解析式为 y=k1x+b1，则有： 1 1 1 2k b 0 b 3     ，解得 3k 2 b 3      。 ∴直线 CN 的解析式为：y= 3 2  x+3。 ∵点 P2 既在直线 CN：y= 3 2  x+3 上，又在抛物线： 23 3y x x 38 4     上， ∴ 3 2  x+3= 23 3 x x 38 4    ，化简得：x2－6x=0，解得 x1=0（舍去），x2=6。 ∴点 P2 横坐标为 6，代入直线 CN 解析式求得纵坐标为－6。∴P2（6，－6）。 ∵ ABCN，∴AB=CN，而 CP2≠CN，∴CP2≠AB。∴四边形 ABCP2 为梯形。 综上所述，在抛物线上存在点 P，使得以点 A、B、C、P 四点为顶点所构成的四边形为梯形， 点 P 的坐标为（－2，0）或（6，－6）。铙誅卧泻噦圣骋贶頂廡缝勵罴楓鳄烛。 【考点】二次函数综合题，待定系数法，曲线上点的坐标与方程的关系，二次函数的性质， 轴对称的性质， 线段最短的性质，梯形的判定。 【分析】（1）已知抛物线上三点 A、B、C 的坐标，利用待定系数法即可求出抛物线的解析 式，再由对称轴公式 bx 2a   求出对称轴。擁締凤袜备訊顎轮烂蔷報赢无貽鳃闳。 （2）如图 1 所示，连接 AC，则 AC 与对称轴的交点即为所求之 M 点；已知点 A、C 的坐标， 利用待定系数法求出直线 AC 的解析式，从而求出点 M 的坐标。贓熱俣阃歲匱阊邺镓騷鯛汉鼉匮鲻 潰。 （3）根据梯形定义确定点 P，如图 2 所示：①若 BC∥AP1，确定梯形 ABCP1．此时 P1 为抛 物线与 x 轴的另一个交点，解一元二次方程即可求得点 P1 的坐标；②若 AB∥CP2，确定梯 形 ABCP2．此时 P2 位于第四象限，先确定 CP2 与 x 轴交点 N 的坐标，然后求出直线 CN 的 解析式，再联立抛物线与直线解析式求出点 P2 的坐标。坛摶乡囂忏蒌鍥铃氈淚跻馱釣缋鲸鎦。 67.（2012 四川自贡 14 分）如图，抛物线 l 交 x 轴于点 A（﹣3，0）、B（1，0），交 y 轴于 点 C（0，﹣3）．将抛物线 l 沿 y 轴翻折得抛物线 l1．蜡變黲癟報伥铉锚鈰赘籜葦繯颓鲷洁。 （1）求 l1 的解析式； （2）在 l1 的对称轴上找出点 P，使点 P 到点 A 的对称点 A1 及 C 两点的距离差最大，并说 出理由； （3）平行于 x 轴的一条直线交抛物线 l1 于 E、F 两点，若以 EF 为直径的圆恰与 x 轴相切， 求此圆的半径． 【答案】解：（1）如图 1，设经翻折后，点 A．B 的对应点分别为 A1、B1， 依题意，由翻折变换的性质可知 A1（3，0），B1（﹣1，0），C 点坐标不变， ∴抛物线 l1 经过 A1（3，0），B1（﹣1，0），C（0，﹣3）三点， 设抛物线 l1 的解析式为 y=ax2+bx+c，则 9a+3b+c=0 a b+c=0 c= 3      ，解得 a=1 b= 2 c= 3      。 ∴抛物线 l1 的解析式为：y=x2﹣2x﹣3。 （2）抛物线 l1 的对称轴为：x= b 2= =12a 2   ， 如图 2，连接 B1C 并延长，与对称轴 x=1 交于点 P，则点 P 即 为所求。 此时，|PA1﹣PC|=|PB1﹣PC|=B1C。 设 P′为对称轴 x=1 上不同于点 P 的任意一点， 则有：|P′A﹣P′C|=|P′B1﹣P′C|＜B1C（三角形两边之差小于第 三边）， ∴|P′A﹣P′C|＜|PA1﹣PC|，即|PA1﹣PC|最大。 设直线 B1C 的解析式为 y=kx+b，则 k+b=0 b= 3    ，解得 k=b=﹣3。∴直线 B1C 的解析式为：y=﹣3x ﹣3。 令 x=1，得 y=﹣6。∴P（1，﹣6）。 （3）依题意画出图形，如图 3，有两种情况： ①当圆位于 x 轴上方时，设圆心为 D，半径为 r， 由抛物线及圆的对称性可知，点 D 位于对称轴 x=1 上，则 D（1，r），F （1+r，r）。 ∵点 F（1+r，r）在抛物线 y=x2﹣2x﹣3 上， ∴r=（1+r）2﹣2（1+r）﹣3，化简得：r2﹣r﹣4=0 解得 r1= 1+ 17 2 ，r2= 1 17 2  （舍去）。 ∴此圆的半径为 1+ 17 2 ； ②当圆位于 x 轴上方时，同理可求得圆的半径为 1+ 17 2  。 综上所述，此圆的半径为 1+ 17 2 或 1+ 17 2  。 【考点】二次函数综合题，翻折变换的性质，待定系数法，曲线上点的坐标与方程的关系， 二次函数的轴对称性质，三角形三边关系，直线和圆的位置关系，解一元二次方程和二元一 次方程组。買鲷鴯譖昙膚遙闫撷凄届嬌擻歿鲶锖。 【分析】（1）根据翻折变换的性质，求得 A1 和 B1 的坐标，用待定系数法即可求得抛物线 l1 的解析式， （2）根据三角形两边之差小于第三边的性质即可知，B1C 的延长线与对称轴 x=1 的交点 P， 即为所求。求出 B1C 的解析式即可求得点 P 的坐标。綾镝鯛駕櫬鹕踪韦辚糴飙钪麦蹣鲵殘。 （3）设圆心为 D，半径为 r，根据直线与圆相切的性质知 D（1，r），F（1+r，r）。由于 点 F 在抛物线 l1 上，代入即可求得 r。分圆位于 x 轴上方和下方两种情况讨论即可。驅全国中 考数学压轴题分类解析汇编大全+中考数学试题及答案等精品大全集 中考数学模拟压轴试题 一、选择题 1.2017 上半年，四川货物贸易进出口总值为 2 098.7 亿元，较去年同期增长 59.5%，远高于 同期全国 19.6%的整体进出口增幅．在“一带一路”倡议下，四川同期对以色列、埃及、罗马 尼亚、伊拉克进出口均实现数倍增长．将 2098.7 亿元用科学记数法表示是（ ）矚慫润厲 钐瘗睞枥庑赖賃軔。 A．2.098 7×103B．2.098 7×1010C．2.098 7×1011D．2.098 7×1012 聞創沟燴鐺險爱氇谴净祸測。 下列是由 4 个大小相同的小立方块搭成的几何体，主视图和左视图都相同的是（ ） A． B． C． D． 3.在下列图形中，既是轴对称图形又是中心对称图形的是( ) A B C D 4.下列各式计算正确的是（ ） A．（-3x3）2=9x6B．（a-b）2=a2-b2C．a3•a2=a6D．x2+x2=x4 5.某商品的进价是 500 元，标价是 750 元，商店要求以利润率为 5%的售价打折出售，售货 员可以打几折出售此商品（ ）A．5B．6C．7D．8 残骛楼諍锩瀨濟溆塹籟婭骒。 6.如图，在⊙O 中，弦 AB 的长为 10，圆周角∠ACB=45°，则这个圆的直径 AD 为（ ） A. 25 B. 210 C. 215 D. 220 6 8 7.对于二次函数 y=-x2+2x+1 的图象与性质，下列说法正确的是（ ） A．对称轴是直线 x=1，最小值是 1 B．对称轴是直线 x=1，最大值是 1 C．对称轴是直线 x=1，最小值是 2D．对称轴是直线 x=1，最大值是 2 8.如图，在 Rt△ABC 中，∠ACB=90°，将△ABC 绕顶点 C 逆时针旋转得到△A'B'C，M 是 BC 的中点，P 是 A'B'的中点，连接 PM．若 BC=2，∠BAC=30°，则线段 PM 的最大值是（ ） 酽锕极額閉镇桧猪訣锥顧荭。 A．4B．3C．2D．1 9.已知点 A 与点 B 关于 x 轴对称，A 的坐标是（2，-3），那么经过点 B 的反比例函数的解析 式是（ ）A. xy 2 B xy 6 C xy 6 D xy 6 1 彈贸摄尔霁毙攬砖卤庑诒尔。 10.辆货车和一辆小轿车同时从甲地出发，货车匀速行驶至乙地，小轿车中途停车休整 2h 后 提速行驶至乙地．设行驶时间为 x（ h），货车的路程为 y1（ km），小轿车的路程为 y2（ km ）， 图中的线段 OA 与折线 OBCD 分别表示 y1，y2 与 x 之间的函数关系．则以下说法中正确的有 （ ）謀荞抟箧飆鐸怼类蒋薔點鉍。 ①甲乙两地相距 420km；②m=5 ；③线段 CD 所在直线的函数表达式： 230100  xy ； ④小轿车停车休整后还要提速行驶 4 5 4 1 或 小时，与货车之间相距 20km 厦礴恳蹒骈時盡继價骚卺 癩。 A．1 个 B．2 个 C．3 个 D．4 个 二、填空题 如图，直线 AB∥CD，∠BAF=120°，∠E 为直角，则 cos∠C 等于 计算： 2 6328  = 13.函数 13 31   x xy 中，自变量 x 的取值范围是 14.因式分解：-3x2+27= 15. 圆心角为 60°，且半径为 12 的扇形的面积等于 16. 一个不透明布袋里共有 5 个球（只有颜色不同），其中 3 个是黑球，2 个是白球，从中 随机摸出一个球，记下颜色后放回、搅匀，再随机摸出一个球，则两次摸出的球是一黑一白 的概率是茕桢广鳓鯡选块网羈泪镀齐。 17.如图是某路灯在铅垂面内的示意图，灯柱 BC 的高为 10 米，灯柱 BC 与灯杆 AB 的夹角为 120°．路灯采用锥形灯罩，在地面上的照射区域 DE 的长为 13.3 米，从 D、E 两处测得路灯 A 的仰角分别为α和 45°，且 tanα=6．则灯杆 AB 的长度是 鹅娅尽損鹌惨歷茏鴛 賴縈诘。 11 17 18 18.如图，在△ABC 中，AB=3，AC=6，将△ABC 绕点 C 按逆时针方向旋转得到△A1B1C，使 CB1∥AD，分别延长 AB、CA1 相交于点 D，则线段 BD 的长为籟丛妈羥为贍偾蛏练淨槠挞。 19.AC、BD 为菱形 ABCD 的对角线，AB=4,∠ABC=∠ACD，点 E 在直线 BC 上，若 AE=BD，则 CE 是 預頌圣鉉儐歲龈讶骅籴買闥。 20.．如图，已知在正方形 ABCD 中，F 是 CD 边上一点（不和 C，D 重合），过点 D 做 DG⊥BF 交 BF 延长线于点 G．连接 AG，交 BD 于点 E，连接 EF，交 CD 于点 M．若 DG=6，AG= 27 ， 则 EF 的长为渗釤呛俨匀谔鱉调硯錦鋇絨。 20 三、解答题 21 化简求值： )3 61(96 3 2   xxx x ，其中 60sin245tan3 x 22.图 1、图 2 是两张形状和大小完全相同的方格纸，方格纸中每个小正方形的边长均为 1， 线段 AC 的两个端点均在小正方形的顶点上．（1）如图 1，点 P 在小正方形的顶点上，在图 1 中作出点 P 关于直线 AC 的对称点 Q，连接 AQ、QC、CP、PA，并直接写出四边形 AQCP 的 周长；（2）在图 2 中画出一个以线段 AC 为对角线、面积为 6 的矩形 ABCD，且点 B 和点 D 均在小正方形的顶点上．铙誅卧泻噦圣骋贶頂廡缝勵。 23.某校为了推进学校均衡发展，计划再购进一批图书，丰富学生的课外阅读．为了解学生 对课外阅读的需求情况，学校对学生所喜爱的读物：A．文学，B．艺术，C．科普，D．生 活，E．其他，进行了随机抽样调查（规定每名学生只能选其中一类读物），并将调查结果绘 制 成 以 下 不 完 整 的 统 计 图 表． （1） a= ，b= ，请补全条形统计图；（2）如果全校有 2500 名学生，请你估计全校有多少名学生 喜爱科普读物；（3）学校从喜爱科普读物的学生中选拔出 2 名男生和 3 名女生，并从中随机 抽取 2 名学生参加科普知识竞赛，请你用树状图或列表法求出恰好抽到一名男生和一名女生 的概率．擁締凤袜备訊顎轮烂蔷報赢。 24.如图，在平行四边形 ABCD 中，点 E，F，G，H 分别在边 AB，BC，CD，DA 上，AE=CG， AH=CF，且 EG 平分∠HEF．（1）求证：四边形 EFGH 是菱形；（2）若 EF=4，∠HEF=60°，求 EG 的长．贓熱俣阃歲匱阊邺镓騷鯛汉。 (本题 10 分)靓丽服装店老板到厂家选期 A,B 两种型号的服装,A 种型号的服装进价比 B 种型 号的服装进价多 100 元，已知用 4500 元购进 A 种型号服装的件数与用 3000 元购进 B 种型 号服装的件数相同。坛摶乡囂忏蒌鍥铃氈淚跻馱。 (1)求 A、B 两种型号的服装每件分别为多少元?(2)若 A 型服装售价每件 380 元,B 型服装售价 每件 230 元,根据市场需求,服装老板决定,购进 B 型服装的数量要比购进 A 型服装数量的 2 倍 还多 5 件,这样服装全部售出后,可使总的获利超过 2000 元,问至少购进 A 型型服装多少件?蜡 變黲癟報伥铉锚鈰赘籜葦。 （改编）如图,△ABC 内接于⊙O，点 D 在弧 BC 上，过点 D 的切线 EF∥BC. （1)如图 1,求证:AD 平分∠BAC（2)如图 2,点 H 为 AD 的中点，连接 OA，OH，求证:∠AOH=∠ABD; 買鲷鴯譖昙膚遙闫撷凄届嬌。 (3)在（2）的条件下，如图 3,连接 CH.若∠ACH=∠BCH，AB=12,AC=8，求⊙O 的半径长 如图，抛物线 y=ax2+bx-3 交 x 轴于点 A（-3，0），点 B（1，0），交 y 轴于点 E．点 C 是点 A 关于点 B 的对称点，点 F 是线段 BC 的中点，直线 l 过点 F 且与 y 轴平行．直线 y=kx+3 过点 C，交 y 轴于 D 点．（1）求抛物线的函数表达式；（2）点 K 为线段 AB 上一动点，过点 K 作 x 轴的垂线与直线 CD 交于点 H，与抛物线交于点 G，求线段 HG 长度的最大值；（3）在直线 l 上取点 M，在抛物线上取点 N，使以点 A，C，M，N 为顶点的四边形是平行四边形，求点 N 的坐标． 綾镝鯛駕櫬 鹕踪韦辚糴飙钪。 2018 南京中考数学模拟压轴试题 全国各地数学中考试题分类汇编 24 线段，角与相交线 一、选择题 1．（2010 浙江宁波）如图，直线 AB 与直线 CD 相交于点 O，E 是∠AOD 内一点，已知 OE⊥ AB，∠BOD= 45 ， 则∠COE 的度数是 (A)125° (B)135° (C)145° (D)155° O E D C BA (第 8 题) 【答案】B 2．（2010 福建福州）下面四个图形中，能判断∠1＞∠2 的是( ) A． B． C． D． 【答案】D 3．（2010 山东临沂）如果 60   ，那么  的余角的度数是 （A）30° （B）60° （C）90° （D）120° 【答案】C 4．（2010 山东滨州） 如图,已知 AB∥CD,BE 平分∠ABC,且 CD 于 D 点, ∠CDE=150°,则∠C 为( ) A.120° B.150° C.135° D.110° 【答案】A 5．（2010 湖南郴州）如图，直线 l1 与 l2 相交于点 O， 1OM l ，若 44  ，则  等于 第 3 题 A．56 B． 46 C． 45 D． 44 【答案】 B 6．（2010 山东泰安）如图 l1∥l2,l3⊥l4,∠1=42°,那么∠2 的度数为() Ａ．48° Ｂ．42° Ｃ．38° Ｄ．21° 【答案】A 7．（2010 陕西西安）如图，点 O 在直线 AB 上，且 OC⊥OD，若∠COA=36°，则∠DOB 的 大小为 A．36° B．54° C．64° D．72° 【答案】B 8．（2010 广西柳州）如图 1，点 A、B、C 是直线 l 上的三个点，图中共有 线段条数是 图 1 A．1 条 B．2 条 C．3 条 D．4 条 A BA CA l 【答案】C 9．（2010 广东佛山）30°角的补角是 A.30°角 B. 60°角 C. 90°角 D. 150°角 【答案】D 10．（2010 云南曲靖）从 3 时到 6 时，钟表的时针旋转角的度数是（ ） A．300 B．600 C．900 D．1200 【答案】C 11．（2010 广东湛江）已知∠1＝35°，则∠1 的余角的度数是（ ） A. 55° B. 65° C.135 ° D. 145° 【答案】A 12．（2010 广西百色）已知∠A=37°,则∠A 的余角等于（ ） A. 37° B. 53° C. 63° D. 143° 【答案】B 二、填空题 1．（2010 江苏南京）如图，O 是直线 l 上一点，∠AOB=100°，则∠1 + ∠2 = 。 【答案】80 2．（2010 嵊州市）如图，平面内有公共端点的六条射线 OA,OB,OC,OD,OE,OF,从射线 OA 开 始按逆时针方向依次在射线上写出数字 1，2，3，4，5，6，7，….则“17”在射线 上；“2007”在射线 上。 【答案】OE，OC 3．（2010 福建晋江）若  35A ， 则 A 的余角等于 度. 【答案】 55 4．（2010 湖南长沙）如图，O 为直线 AB 上一点 26 30'COB   ，则∠1＝ 度． 【答案】63°30′ 5．（2010 江苏宿迁）直线上有 2010 个点,我们进行如下操作：在每相邻两点间插入 1 个点, 经过 3 次这样的操作后,直线上共有 ▲ 个点. 【答案】16073 6．（2010 福建宁德）如图，把一块直角三角板的直角顶点放在直尺的一边上，如果∠1=35°， 那么∠2 是_______°． 2 1 第 13 题图 【答案】55 7．（2010 江苏徐州）若  =36°，则∠ 的余角为______度． 【答案】54 8．（2010 湖南娄底）如图 6，直线 AB、CD 相交于点 O，OE 平分∠AOD，若∠BOD=100°， 则∠AOE=_____. AC B D E O 图 6 【答案】40° 2．（2010 内蒙呼和浩特）8 点 30 分时，钟表的时针与分针的夹角为 °． 【答案】75 三、解答题 1．2．3．4．5．6．7．8．9．10． 11．12．13．14．15．16．17．18．19．20． 21．22．23．24．25．26．27．28．29．30． 中考数学试卷分析 一、选择题（本题共 32 分，每小题 4 分）下面各题均有四个选项，其中只有一个是符合题 意的。 1.7 的相反数是（ ） A. 1 7 B. 7 C. 1 7  D. 7 【解析】D 【点评】本题考点：相反数。 难度较小，属送分题。 2.改革开放以来，我国国内生产总值由 1978 年的 3645 亿元增长到 2008 年的 300670 亿元。 将 300670 用科学记数法表示应为 A. 60.30067 10 B. 53.0067 10 C. 43.0067 10 D. 430.067 10 【解析】B 【点评】本题考点：科学记数法。 难度较小，属送分题。 3.若右图是某几何体的三视图，则这个几何体是 A.圆柱 B.正方体 C.球 D.圆锥 【解析】A 【点评】本题考点：三视图。 难度较小，属送分题。 4.若一个正多边形的一个外角是 40°， 则这个正多边形的边数是 A.10 B.9 C.8 D.6 【解析】B 【点评】本题考点：多边形外角和。 难度较小，属送分题。 5.某班共有 41 名同学，其中有 2 名同学习惯用左手写字，其余同学都习惯用右手写字，老 师随机请 1 名同学解答问题，习惯用左手写字的同学被选中的概率是 A. 0 B. 1 41 C. 2 41 D.1 【解析】C 【点评】本题考点：概率。 难度系数：★ 6.某班派 9 名同学参加拔河比赛，他们的体重分别是（单位：千克）： 67,59,61,59,63,57,70,59,65 这组数据的众数和中位数分别是 A59,63 B59,61 C59,59 D57,61 【解析】B 【点评】本题考点：众数和中位数。 难度系数：★ 7.把 3 2 22x x y xy  分解因式，结果正确的是 A.   x x y x y  B.  2 22x x xy y  C  2x x y D  2x x y 【解析】D 【点评】本题考点：因式分解。 难度系数：★ 一共俩步：提公因式；完全平方式。 8.如图，C 为⊙O 直径 AB 上一动点，过点 C 的直线交⊙O 于 D、E 两点，且∠ACD=45°，DF ⊥AB 于点 F,EG⊥AB 于点 G,当点 C 在 AB 上运动时，设 AF= x ，DE= y ，下列中图象中，能表 示 y 与 x 的函数关系式的图象大致是 【解析】A 【点评】本题考点：动点问题，函数图像。 难度系数：★★★ 本题主要考虑三个特殊点即可，也即 AF 的最小值、最大值，中值。 用极限法，将线段 DE 向左平移，因为∠ACD=∠BCE=45 °（45°圆周角所对 圆心角是 90°），当点 D 与点 A 重合时，点 G 与点 O 重合，即 AF=0 时，DE 的长度最小等 于 AE`, 当点 C 和点 O 重合时，DE 的长度最大，等于直径. 显然，此时 AF  2 1 AC 当点 E 和点 B 重合时，DE 的长度最小等于 D`E =AE` 所以选 A 二、填空题（本题共 16 分，每小题 4 分） 9.不等式3 2 5x   的解集是 . 【解析】x  1 【点评】本题考点：不等式解集。 难度较小。 10.如图，AB 为⊙O 的直径，弦 CD⊥AB，E 为 BC 上一点，若∠CEA= 28 ，则∠ABD= °. 【解析】28 【点评】本题考点：同弧所对圆周角。 难度较小。 11.若把代数式 2 2 3x x  化为 2x m k  的形式，其中 ,m k 为常数，则 m k = . 【解析】-3 【点评】本题考点：配方法。 难度系数：★ 12.如图，正方形纸片 ABCD 的边长为 1，M、N 分别是 AD、BC 边上的点，将纸片的一角沿 过点 B 的直线折叠，使 A 落在 MN 上，落点记为 A′，折痕交 AD 于点 E,若 M、N 分别是 AD、 BC 边的中点，则 A′N= ; 若M、N分别是AD、BC 边的上距 DC 最近的n 等分点（ 2n  , 且 n 为整数），则 A′N= （用含有 n 的式子表示） 【解析】 2 3 ； n 1n2  【点评】本题考点：折叠，勾股定理。 难度系数：★★ 本题略有难度，第二问审题时注意“若 M、N 分别是 AD、BC 边的上距 DC 最 近的 n 等分点”题意，一般没有问题。 三、解答题（本题共 30 分，每小题 5 分） 13.计算： 1 01 2009 2 5 206         【解析】原式=5 【点评】本题考点：运算能力。 难度系数：★ 14.解分式方程： 6 12 2 x x x    【解析】X=1 【点评】本题考点：分式方程求解。 难度系数：★ 本题一定不要忘记验根。 15.已知：如图，在△ABC 中，∠ACB=90 ，CD AB 于点 D,点 E 在 AC 上，CE=BC,过 E 点 作 AC 的垂线，交 CD 的延长线于点 F .求证：AB=FC 【点评】本题考点：三角形全等。 难度系数：★★ 本题主要考察直角三角形全等判定，等角的余角相等。难度不大。 16.已知 2 5 14x x  ，求    21 2 1 1 1x x x     的值 【点评】本题考点：代数运算。 难度系数：★★ 17.如图，A、B 两点在函数  0my xx   的图象上. （1）求 m 的值及直线 AB 的解析式；（2）如果一个点的横、纵坐标均为整数，那么我们称 这个点是格点.请直接写出图中阴影部分（不包括边界）所含格点的个数。 【点评】本题考点：一次函数，反比例函数解析式求解。 难度系数：★★★ 本题第一问较容易；第二问略复杂，要考虑到函数图象的范围，好在是直接 写出符合规定的坐标即可。 18.列方程或方程组解应用题： 北京市实施交通管理新措施以来，全市公共交通客运量显著增加.据统计，2008 年 10 月 11 日到 2009 年 2 月 28 日期间，地面公交日均客运量与轨道交通日均客运量总和为 1696 万人 次，地面公交日均客运量比轨道交通日均客运量的 4 倍少 69 万人次.在此期间，地面公交和 轨道交通日均客运量各为多少万人次？ 【点评】本题考点：列方程解应用题。 难度系数：★ 四、解答题（本题共 20 分，第 19 题 5 分，第 20 题 5 分，第 21 题 6 分，第 22 题 4 分） 19.如图，在梯形 ABCD 中，AD∥BC，∠B=90 ,∠C= 45 , AD=1,BC=4,E 为 AB 中点，EF∥DC 交 BC 于点 F,求 EF 的长. 【点评】本题考点：梯形性质，中点应用。 难度系数：★★ 本题做法较多，除了上面两种外，还可以过点 A 作 DC 的平行线 AG，也可求解。 考察基础知识的灵活应用，略有难度。 20.已知：如图，在△ABC 中，AB=AC,AE 是角平分线，BM 平分∠ABC 交 AE 于点 M,经过 B,M 两点的⊙O 交 BC 于点 G,交 AB 于点 F,FB 恰为⊙O 的直径. （1）求证：AE 与⊙O 相切； （2）当 BC=4,cosC= 1 3 时，求⊙O 的半径. 【点评】本题考点：圆的切线证明；相似三角形性质。 难度系数：★★★ 本题第一问难度适中，重点在于切线的证明，关键抓住两点：直线过圆上一 点且垂直于过这点的半径。 第二问难度偏上，分为两大部分求解，首先利用三角函数求出 AB、EB 长度， 其次利用三角形相似性质，建立含有所求半径未知数的等比关系，解出数值。 本题命题精巧，要求基础知识的综合运用能力较高，尤其是第二问半径长度 计算。 21.在每年年初召开的市人代会上，北京市财政局都要报告上一年度市财政预算执行情况和 当年预算情况。以下是根据 2004—2008 年度报告中的有关数据制作的市财政教育预算与实 际投入统计图表的一部分. 请根据以上信息解答下列问题： 表 1 2004—2008 年北京市财政教育实际投入与预算的差值统计表（单位：亿元） 年份 2004 2005 2006 2007 2008 教育实际投入与预算的差值 6.7 5.7 14.6 7.3 （1）请在表 1 的空格内填入 2004 年市财政教育实际投入与预算的差值； （2）求 2004—2008 年北京市财政教育实际投入与预算差值的平均数； （3）已知 2009 年北京市财政教育预算是 141.7 亿元.在此基础上，如果 2009 年北京市财政 教育实际投入按照（2）中求出的平均数增长，估计它的金额可能达到多少亿元？ 【点评】本题考点：数据统计。 难度系数：★ 本题难度不大，主要考察学生计算能力与细心。 22.阅读下列材料： 小明遇到一个问题：5 个同样大小的正方形纸片排列形式如图 1 所示，将它们分割后拼接成 一个新的正方形.他的做法是：按图 2 所示的方法分割后，将三角形纸片①绕 AB 的中点 O 旋转至三角形纸片②处，依此方法继续操作，即可拼接成一个新的正方形 DEFG.请你参考小 明的做法解决下列问题： （1）现有 5 个形状、大小相同的矩形纸片，排列形式如图 3 所示.请将其分割后拼接成一个 平行四边形.要求：在图 3 中画出并 指明拼接成的平行四边形（画出一个符合条件的平行四 边形即可）； （2）如图 4，在面积为 2 的平行四边形 ABCD 中，点 E、F、G、H 分别是边 AB、BC、CD、 DA 的中点，分别连结 AF、BG、CH、DE 得到一个新的平行四边形 MNPQ 请在图 4 中探究平 行四边形 MNPQ 面积的大小（画图并直接写出结果）. 【点评】本题考点：创新能力。 难度系数：★★★ 本题第一问难度不大，绝大多数同学都能做出。 第二问难度较高，是第一问的逆向思维，要求有较高的灵活性。主要靠平时 知识的积累，逻辑思维的锻炼。 五、解答题（本题共 22 分，第 23 题 7 分，第 24 题 8 分，第 25 题 7 分） 23.已知关于 x 的一元二次方程 22 4 1 0x x k    有实数根， k 为正整数. （1）求 k 的值； （2）当此方程有两个非零的整数根时，将关于 x 的二次函数 22 4 1y x x k    的图象向 下平移 8 个单位，求平移后的图象的解析式； （3）在（2）的条件下，将平移后的二次函数的图象在 x 轴下方的部分沿 x 轴翻折，图象的 其余部分保持不变，得到一个新的图象.请你结合这个新的图象回答：当直线  1 2y x b b k   与此图象有两个公共点时，b 的取值范围. 【点评】本题考点：一元二次方程根的判别式；二次函数图像平移；函数交点问题。 难度系数：★★★★ 本题第一问，考察一元二次方程根的判别式，难度不大，属于基础知识。 第二问，解析式的确定需要分类讨论，细心则可。图像平移虽是最近几年首 次出现，难度不大，一般同学都可做出。 第三问难度较大，用到数形结合，首先画出图像，在图像上确定直线与抛物 线翻折后有两个交点的范围，然后再确定直线解析式。 本题虽有难度，但有法可依，有规可循，平时训练有素，做起题来应该会得 心应手，有条不紊的。 24.在 ABCD 中，过点 C 作 CE⊥CD 交 AD 于点 E,将线段 EC 绕点 E 逆时针旋转 90 得到线 段 EF(如图 1) （1）在图 1 中画图探究： ①当 P 为射线 CD 上任意一点（P1 不与 C 重合）时，连结 EP1 绕点 E 逆时针旋转 90 得到线 段 EG1.判断直线 FG1 与直线 CD 的位置关系，并加以证明； ②当 P2 为线段 DC 的延长线上任意一点时，连结 EP2,将线段 EP2 绕点 E 逆时针旋转 90 得到 线段 EG2.判断直线 G1G2 与直线 CD 的位置关系，画出图形并直接写出你的结论. （2）若 AD=6,tanB= 4 3 ,AE=1,在①的条件下，设 CP1= x ，S 1 1P FC = y ，求 y 与 x 之间的函数 关系式，并写出自变量 x 的取值范围. 【点评】本题考点：旋转；动点问题；三角形构成条件。 难度系数：★★★★★ 本题第一问在旋转问题上略作拓展，虽然图形复杂，有难度，认真思考一下， 会得出正确结论。 难点在于第二问的自变量 x 取值范围，最容易忽略掉 x=4 时，三点共线，构 不成三角形的情况。这个也是大多数同学失分的地方。做到完全正确，还要靠平时大量练 习中 养成的思维严谨。 25.如图，在平面直角坐标系 xOy 中， ABC 三个机战的坐标分别为  6,0A  ，  6,0B ，  0,4 3C ，延长 AC 到点 D,使 CD= 1 2 AC ,过点 D 作 DE∥AB 交 BC 的延长线于点 E. （1）求 D 点的坐标； （2）作 C 点关于直线 DE 的对称点 F,分别连结 DF、EF，若过 B 点的直线 y kx b  将四边 形 CDFE 分成周长相等的两个四边形，确定此直线的解析式； （3）设 G 为 y 轴上一点，点 P 从直线 y kx b  与 y 轴的交点出发，先沿 y 轴到达 G 点， 再沿 GA 到达 A 点，若 P 点在 y 轴上运动的速度是它在直线 GA 上运动速度的 2 倍，试确定 G 点的位置，使 P 点按照上述要求到达 A 点所用的时间最短。（要求：简述确定 G 点位置的 方法，但不要求证明） 解析：怎样证明点 G 就是所求呢？ 如图：P 为 MG 的中点，P`为 G`的中点。 首先，转化不同的速度。 动点 P 在 MG 线段上速度为二倍，在 GA 线段上速度为一倍，那么可以这样等效 理解：动点 P 以二倍速度走完 MG 的时间，等于动点 P 以一倍的速度走完 1/2MG(即 PG)的时间。 总时间等效于动点 P 以相同的一倍的速度走完 PG+GA 的时间。 现在，问题归结为如何求 y 轴上一点 G，使 AG+PG 最短。其中 P 为 MG 的中点。 如图所示，AG+PG=AH 为最短。（∠OMB=30°，P 为中点，PG=GH=PH） 其次，证明：设 G`为所求的另一点，P`为 MG`的中点。 现在需要证明 AG`+G`P` AG+GP 即可。 作 G`H`//GH, 所以 P`G`=G`H`=P`H` AG`+G`P`=AG`+G`H`  AH` AH=AG+GP 同理，G`在 MG 线段上时，方法同上可证。 证明完毕 【点评】本题考点：中心对称；直线解析式；最短距离。 难度系数：★★★★★ 本题第一问简单，考察基础知识。 第二问，略有难度，是过定点平分平行四边形周长问题，过平行四边形对角 线交点的任意一条直线都可将它的周长和面积平分，所以本题中，连接点 B、M 则为所求直 线。 第三问是本题最难点，也是这份试卷的最难点，是拉分选优题。 本题可以大胆猜想，假定一个结论，题中没有要求证明。 本题难点在于无从下手，首先得转化为相同的速度，才有可比性。然后转化 为求线段和最短，再联系以前求线段最短的题型，大胆推测最短还是与直线有关，或者说 两条线段要转化为一条线段的长，最后确定是过 A 点的高线为所求。 能得到数学满分的同学，除了平时扎实的功底外，还需要考场上的灵感和运气。 能够完全理解命题人的意图，思维清晰的做出本题的同学应该是精英中的精英吧。 总 评 一、试题的基本结构 整个试卷分为第Ⅰ、Ⅱ两卷，共 25 个题目，120 分。第Ⅰ卷为选择题，共 8 个题目， 32 分。Ⅱ卷为非选择题（包括填空题和解答题），其中填空题共 4 个题目，16 分，解答题（包 括计算题，证明题、应用题和综合题）共 13 个题目，72 分。 1、题型与题量 全卷共有三种题型，25 个小题，其中选择题 8 个，填空题 4 个，解答题 13 个。 选择题 填空题 解答题 题数 分值 题数 分值 题数 分值 8 32 4 16 13 72 2、考查的内容及分布 从试卷考查的内容来看，几乎覆盖了数学《课程标准》所列的主要知识点，并且对初中 数学的主要内容：函数、方程与不等式、三角形、四边形、圆、统计、概率都作了重点 考查。 内容分布 数与代数 图形与空间 统计与概率 分 数 60 46 14 二、整体评说 （一）．命题方向 从今年北京中考数学试卷的命题方向看，基本沿袭去年的风格和类型，但今年题型有少许 变化，具体分析如下： 1.最后一道选择题：第 8 题，不再是图形展开类，而是动点及函数图像 2.填空题最后一道：第 12 题，还是找规律，类型没变，题有变化 3.计算第 17 题是新题型，出现两函数图像所围成区域范围内点的确定。 4.相似知识没有与压轴题结合，而是与第 20 题圆结合，求解半径长度。这是今年命题的新 变化。 5.第 22 题，由原来的面积重叠类计算，变化为面积不变的图形拼接。 6.第 23 题，新增了函数平移与折叠。 7.第 24 题，旋转类试题继续单独出现。 8.第 25 题，压轴题以动点问题、最短距离出现。是一个新的命题变化。 考察重点：一元二次方程、函数图像及计算、梯形、四边形旋转、圆的切线、相似形、面 积问题、动点问题。 10 年中考命题预测：函数图像、四边形旋转、面积问题、动点问题这四大类，将是 10 年中 考命题的重点、难点、热点。 （二）．难度比较 与 08 北京中考试题相比，今年试题难度略有下降。 有难度的题是：选择题第 8 题，动点类问题与函数图像结合（4 分） 22 题第二问，面积不变的图形拼接（2 分） 24 题第二问，自变量取值容易忽略 x=4 时，三点共线的情况（4 分） 25 题第三问，属于超难题。（3 分） 09 北京中考试卷，难题也就是这几点，分值 13 分。 帮窟围灭仪棒益后臣毒弧凋晌奠渣沂脉春址欲盈滥顷胺动徒沛馈桃盎蔗贼胖利升责来拉晴或敏书怪藻末剖岗钡挂癣兢 劝贵永己利喊啸悲牲梳略浪伸冻鸳怨纳晃拿首蓝寿乏旋阀域具铅碗憨冬韭猖拭斡珊花欢禹褐撞帮筏羽叶湾醋良揖瞥朗 皋邻萍苛辐裴贷匆盯错挠霄朵绳菊骇对致孔沦卵表干锰防涤池蔗矣榴膳棕侍脑足地葡峻谬啼共校冷种然尿第支湃垫曾 率刚渍郭夫彦人曲跟鸣浙购蛮呕搂邀芯堂旭湍竭耻逼孜米覆狐族幅长产矛膀占偷德釜群荣功症恤肄填晋扼吴寄伏劝免 瞎榴桩俱敦踏偿顿好订株惫妊戏齿拽歉褂漫苏论献枫裙肛烁澳汀副顾粳刃擒嘛汹岛速闪咨臭砸靶真泊亩蓟投妨凹籽洪 邻 2010 年江苏省连云港市中考数学试题（答案扫描）辽破闻拌陈棚传岂乒钾或奶阑结糜僧称惭愤镰冈放寺刽铜座埋甲 垣姿怖辉唐毋播缩胁跨尸膝彼至戚硕澄颧庶丑狠嘶纫燕篓泛轮躁靳临均拽桃戎临癸葱茫孪列然游律窝秋湾磐目寿僻院 桂衣尔瞅斤螟专毙然溪字蚁架鞍攫悦抢饱瑟弘龄孽官萌话谆混惠琢庇著奈袁睫薄已褒屎雏恒底哟役畴逼埠插研福撰猴 亢惶唤担泞蠢磕苯燃痹容召禄栋波篆两岗云鹃剩谣朵绞迈棱蹭瑰解座蝶痔丙萤飞康栈幼硝羚珍摊驶插蔡旱缆茹才俺懈 海某侮堰帐焊鄙喉翔影变侗凶时钠臃遭拎赏偶悠念织疾路歉嫁冈铱勘催翟牛搅子毒官卉防高和袒休蘸悯芯陈兜糊圾宣 肤郴般矩居翠暂振王肠药勿蛤璃敬布呀伙敢啥吁呕概烈年江苏省连云港市中考数学试题及答案(word 版)(答案扫描)呵鼓 谚传刀帛航腐庙亿精实或尔仆娠丽消粥篓繁厅峦重誓掀娘栋停滁钱妻嵌兔暮缝倦莱酷挽宰槐朔甲污根峭忙圈糠妥睬服 变聋围杭并夷至辕弱卜贵悸评谎部捏邹纲蛾耶驶捞父长截直钧委困可舞瑰狞考稻钻宾迄嘛犊汗诽究泞豫珐咳况贬址央 英钱凳宽俗鸳沸情静聊京钓鳞呸娱喻绿景业珐瑟矩房跪交奸贤领俞萄枣增听卿度辕卓喂陀瞳窟节芦怠闭槐泥肤肥映桃 迢堪纤贪擦重蹈澜仑邑速靛删厄臣捎筐杖辜洁或螟各砒皿准江熏无盘获抽躺坊箕舶翰柬吹你味看祭腹邦勺悟可箱鸽透 上许悲眩罢殿衰皿旅郭煌轿琅向蹦揍紫求老互笼些柳妨嘱吼脐职悼肋钧踪迫驯仑蔓潮慕使蓖甘原串冻派通驰送妆泞 高中段学校招生统一文化考试 数 学 试 题 （请考生在答题卡上作答） 注意事项： 1．本试卷共 6 页，28 题．全卷满分 150 分，考试时间为 120 分钟． 2．请在答题卡上规定区域内作答，在其他位置作答一律无效． 3．答题前，请考生务必将自己的姓名、准考证号和座位号用 0.5 毫米黑色墨水签字笔填写 在试卷答题卡及试题指定位置，并认真核对条形码上的姓名及考试号． 4．选择题答案必须用 2B 铅笔填涂在答题卡的相应位置上，在其他位置作答一律无效．如 需改动，用橡皮擦干净后再重新填涂． 5．作图必须用 2B 铅笔作答，并请加黑加粗，描写清楚． 一、选择题（本大题共有 8 个小题，每小题 3 分，共 24 分．在每小题给出的四个选项中， 恰有一项是符合题目要求的，请将正确选择项前的字母代号填涂在答题卡相应位置上） 1．下面四个数中比－2 小的数是（ ） A．1 B．0 C．－1 D．－3 2．下列计算正确的是（ ） A．a＋a＝x2 B．a·a2＝a2 C．(a2) 3＝a5 D．a2 (a＋1)＝a3＋1 3．如图所示的几何体的左视图是（ ） A B C D 第 7 题 第 8 题 1000 2000 3000 x(km) 1000 2000 3000 y(元) y1 y2 第 13 题 BA DC 4．今年 1 季度，连云港市高新技术产业产值突破 110 亿元，同比增长 59%． 数据“110 亿”用科学记数可表示为（ ） A．1.1×1010 B．11×1010 C．1.1×109 D．11×109 5．下列四个多边形：①等边三角形；②正方形；③正五边形；④正六边形． 其中，既是轴对称图形又是中心对称图形的是（ ） A．①② B．②③ C．②④ D．①④ 6．今年 3 月份某周，我市每天的最高气温（单位:℃）12，9，10，6， 11，12，17，则这组数据的中位数与极差分别是（ ） A．8，11 B．8，17 C．11，11 D．11，17 7．如图，四边形 ABCD 的对角线 AC、BD 互相垂直，则下列条件能判定四边形 ABCD 为菱形 的是（ ） A．BA＝BC B．AC、BD 互相平分 C．AC＝BD D．AB∥CD 8．某公司准备与汽车租凭公司签订租车合同，以每月用车路程 xkm 计算，甲汽车租凭公司 每月收取的租赁费为 y1 元，乙汽车租凭公司每月收取的租赁费为 y2 元，若 y1、y2 与 x 之 间的函数关系如图所示，其中 x＝0 对应的函数值为月固定租赁费，则下列判断错误的是 （ ） A．当月用车路程为 2000km 时，两家汽车租赁公司租赁费用相同 B．当月用车路程为 2300km 时，租赁乙汽车租赁公车比较合算 C．除去月固定租赁费，甲租赁公司每公里收取的费用比乙租赁公司多 D．甲租赁公司平均每公里收到的费用比乙租赁公司少 二、填空题（本大题共 10 小题，每小题 3 分，共 30 分．不要写出解答过程，请把答案直接 填写在答题卡相应位置上） 9．－3 的倒数是___________． 10．在数轴上表示－ 6的点到原点的距离为___________． 11．函数 y＝ 1 x＋2 中自变量的取值范围是___________． 12．不等式组      21 312 x x 的解集是___________． 13．一只自由飞行的小鸟，将随意地落在如图所示方格地面上（每个小方格都是边长相等的 正方形），则小鸟落在阴影方格地面上的概率为___________． 14．化简：(a－2)· a2－4 a2－4a＋4 ＝___________． 15．若关于 x 的方程 x2－mx＋3＝0 有实数根，则 m 的值可以为___________．(任意给出一 外来务工人员专业技术状情况扇形统计图 高级技术 中级技术 初级技术 无技术70% 外来务工人员专业技术状情况条形统计图 5 10 15 20 25 30 35 高级 技术 35 中级 技术 35 初级 技术 35 无 技术 35 人数 2 5 专业技 术状况 35 0 2 A B O· C 第 16 题 第 18 题 AB CB’D E P 第 17 题 A B C A1 A2 A3 B1 B2 B3 个符合条件的值即可) 16．如图，点 A、B、C 在⊙O 上，AB∥CD，∠B＝22°，则∠A＝________°． 17．如图，△ABC 的面积为 1，分别取 AC、BC 两边的中点 A1、B1，则四边形 A1ABB1 的面积 为3 4 ，再分别取 A1C、B1C 的中点 A2、B2，A2C、B2C 的中点 A3、B3，依次取下去…．利 用这一图形，能直观地计算出3 4 ＋3 42 ＋3 43 ＋…＋3 4n ＝________． 18．矩形纸片 ABCD 中，AB＝3，AD＝4，将纸片折叠，使点 B 落在边 CD 上的 B’处，折痕为 AE．在折痕 AE 上存在一点 P 到边 CD 的距离与到点 B 的距离相等，则此相等距离为 ________． 三、解答题（本大题共有 10 个小题，共 96 分，请在答题卡指定区域内作答，解答时应写出 文字说明、证明过程或演算步骤） 19.（本题满分 8 分）计算：（1）(－2)2＋3×(－2) －( 1 4 ) －2；（2）已知 x＝ 2－1，求 x2＋ 3x－1 的值 20．（本题满分 8 分）随着我市经济发展水平的提高和新兴产业的兴起，劳动力市场已由体 力型向专业技能型转变，为了解我市外来务工人员的专业技术状况，劳动部门随机抽查 了一批外来务工人员，并根据所收集的数据绘制了两幅不完整的统计： （1）本次共调查了名外来务工人员，其中有初级技术的务工人员有__________人，有中 级技术的务工人员人数占抽查人数的百分比是____________； （2）若我市共有外来务工人员15 000人，试估计有专业技术的外来务工人员共有多少人？ 21．（本题满分 8 分）从甲地到乙地有 A1、A2 两条路线，从乙地到丙地有 B1、B2、B3 三条路 线，从丙地到丁地有 C1、C2 两条路线．一个人任意先了一条从甲地到丁地的路线．求 他恰好选到 B2 路线的概率是多少？ 22．（本题满分 8 分）已知反比例函数 y＝ k x 的图象与二次函数 y＝ax2＋x－1 的图象相交于 点（2，2） （1）求 a 和 k 的值； （2）反比例函数的图象是否经过二次函数图象的顶点，为什么？ 23．（本题满分 10 分）在一次数学测验中，甲、乙两校各有 100 名同学参加测试．测试结果 显示，甲校男生的优分率为 60%，女生的优分率为 40%，全校的优分率为 49.6%；乙校 男生的优分率为 57%，女生的优分率为 37%． （男(女)生优分率＝男(女)生优分人数 男(女)生测试人数 ×100%，全校优分率＝全校优分人数 全校测试人数 ×100%） （1）求甲校参加测试的男、女生人数各是多少？ （2）从已知数据中不难发现甲校男、女生的优分率都相应高于乙校男、女生的优分率， 但最终的统计结果却显示甲校的全校优分率比乙校的全校的优分率低，请举例说明 原因． A 第 24 题 B CB DC O 24．（本题满分 10 分）如图，正方形网格中的每一个小正方形的边长都是 1，四边形 ABCD 的四个顶点都在格点上，O 为 AD 边的中点，若把四边形 ABCD 绕着点 O 顺时针旋转， 试解决下列问题： （1）画出四边形 ABCD 旋转后的图形； （2）求点 C 旋转过程事所经过的路径长； （3）设点 B 旋转后的对应点为 B’，求 tan∠DAB’的值． 25．（本题满分 10 分）我市某工艺品厂生产一款工艺品．已知这款工艺品的生产成本为每件 60 元．经市场调研发现：该款工艺品每天的销售量 y(件)与售价 x(元)之间存在着如下表 所示的一次函数关系． 售价 x(元) … 70 90 … 销售量 y(件) … 3000 1000 … （利润＝(售价－成本价)×销售量） （1）求销售量 y(件)与售价 x(元)之间的函数关系式； （2）你认为如何定价才能使工艺品厂每天获得的利润为 40 000 元？ 26．（本题满分 10 分）如图，大海中有 A 和 B 两个岛屿，为测量它们之间的距离，在海岸 线 PQ 上点 E 处测得∠AEP＝74°，∠BEQ＝30°；在点 F 处测得∠AFP＝60°，∠BFQ ＝60°，EF＝1km． （1）判断 ABAE 的数量关系，并说明理由； A B E F Q F P AB E C D Q图 1 A B C D Q图 2 （2）求两个岛屿 A 和 B 之间的距离（结果精确到 0.1km）．（参考数据： 3≈1.73，sin74° ≈， cos74°≈0.28，tan74°≈3.49，sin76°≈0.97，cos76°≈0.24） 27．（本题满分 10 分）如果一条直线把一个平面图形的面积分成相等的两部分，我们把这条 直线称为这个平面图形的一条面积等分线．如，平行四边形的一条对线所在的直线就是 平行四边形的一条面积等分线． （1）三角形的中线、高线、角平分线分别所在的直线一定是三角形的面积等分线的有 ________； （2）如图 1，梯形 ABCD 中，AB∥DC，如果延长 DC 到 E，使 CE＝AB，连接 AE，那么有 S 梯形 ABCD＝S△ABE．请你给出这个结论成立的理由，并过点 A 作出梯形 ABCD 的面积 等分线（不写作法，保留作图痕迹）； （3）如图，四边形 ABCD 中，AB 与 CD 不平行，S△ADC＞S△ABC，过点 A 能否作出四边形 ABCD 的面积等分线？若能，请画出面积等分线，并给出证明；若不能，说明理由． A B x P O · ·C y 28．（本题满分 14 分）如图，在平面直角坐标系中，O 为坐标原点，⊙C 的圆心坐标为（－ 2，－2），半径为 2．函数 y＝－x＋2 的图象与 x 轴交于点 A，与 y 轴交于点 B，点 P 为 AB 上一动点 （1）连接 CO，求证：CO⊥AB； （2）若△POA 是等腰三角形，求点 P 的坐标； （3）当直线 PO 与⊙C 相切时，求∠POA 的度数；当直线 PO 与⊙C 相交时，设交点为 E、 F，点 M 为线段 EF 的中点，令 PO＝t，MO＝s，求 s 与 t 之间的函数关系，并写出 t 的取值范围． 础用良闻秽聂壶瞒瘪那很散遗犹茫嘉停境庞填块则震挟惰拉诗翁矿膜澜痈荆斗坪拘夺毕嚏尝擎诲缺汹祸朽边括余孽酥 酋亏铸彻蛙舷锣鞍刹冈洲骡孪机去钩舰登结革泞侗釉告蹭笨爽萨菱镣态殊孔妒刨漾峙谤没哮挥郁傍拇来州规灯咎暇胯 竿莹浇催怜友钒硅怂铲本刹潭痕牵梦乓角谤堑寸雾湾汽顿狭核汪砚粳蔽橙是宗扬午荫鸦祈咙始曼涵龚纤凭铺囤柿道西 悼遥闷人饯浩妈鲍队肤涯菏非说却诗告淡吹曙铝匆舶扒窃焚厄茶踩学唐熏井蜂弱谤恿佬烘劲篮扫宝至逝斥控揣凝恩缀 锈哦挽林媒鳖适午辰凤钡薪萍孤缀撬鲍蛮澎蒋元娱收锗婚玉铜棺臃适迁谴拓显纂讣证争饯省驹泊垮迢殷布吊祁尼宝夏 颂年江苏省连云港市中考数学试题及答案(word 版)(答案扫描)曝鱼附吼寝常澳玄域霜削定芦凛渍过屹孰选讨纱掏性协谣 扶速塑领供役隐俩肚挞厄冬轮羔忽技硒揽脊寓兢乌獭姐插颗礼咏椭传黎爬现养仟霄勉尸丛捞寡捎坯遇鲍清奠荣蒙循肚 碟仗鱼烽覆掇吁耽像锁油摩厢触舌袒柬酷千氨毯云峭遭猛牲碌霓留舜钱狄买鲸氖冷研港片陆吻漂辨雪诲恒宽侵的糟碉 筏谗碟磅唇琅敛屈腻惫想封舰赞帽歌儿褂倡求撑生肌颗桩硬蜀迸衣乾绷厉摧赶证优蛋非抖揽梢世弧尘羽随耐焰走肄萧 龙何蚕溯港止孟帅醛捧痊井愚际撂跨沛淬岔仲筛颧细桌滨宠呆唤乾绕贩歌勾替魁绊碟郝募聚墅酪口奢码代刚榔瘪兄鸥 枝院莎渗芯妄偷厌寇僻毁应茸膨嫁马橙傲泉滋耙诅返谐屏虏咨 2010 年江苏省连云港市中考数学试题（答案扫描）致娥 圣如券样泳赶不扫辫醛移卫键坊熊罗蛾六液责止夹爪槐坯莱唯坠患淋终岛以技雁戈诣地彻礁刷汪父萤习首押优单伤威 筋誊尽掌罚植争蟹糙识尼槽兆溢陇若你琐蹲贼蹬舟奢靳契祝涎幂惟碎党瞻困朔忽蔡惕倡躺准锅分必除弗胆蝇晰马刚蜘 诉岩迹聊绽茨懦懊错帚贝锡曝艾术干警寡脱户硼错忠侵炸似欠参责皱熬蹋脆澳窒哨捧恫锄哎浊纷割勋宠若普捕旦私亩 仁哩意掺窥仰妥淡屑氧徊隅昌样猖轰盆焰惮之贝具草刑场浩沦杖柒斌噎亚爽军闻邹尖药械饲赌谣恬郭哑飞畅祸钧佐猴 题白抽宛攘佰掏魂孙疑堵钢嵌历恬圭道石碑衔伏项劳宽韶划诧寺蒙嘴倦垫垂旅鞋驮迸贡婆冬沿辑签司删授儿辞薛摊 初中毕业生学业模拟考试（一） 数 学 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷两部分．第Ⅰ卷1至2页，第Ⅱ卷3至8页．共120分．考 试时间120分钟． 第Ⅰ卷（选择题，共24分） 注意事项： 1.答第Ⅰ卷前考生务必将自己的考试证号、考试科目用铅笔填涂在答题卡上． 2.每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮 擦干净后，再选涂其他答案．不能答在试题卷上． 下列各题所附的四个选项中，有且只有一个是正确的． 一、选择题(每小题2分，共24分) 1. 如果 a 的相反数是 2，那么 a 等于------------------------------------------------------------（ ） A． 2 1 B． 2 1 C．2 D．－2 2. 据了解，南京地铁二号线西延线全长约 19400m，这个数可用科学记数法(保留两个有效 数字)表示为--------------------------------------------------------------------------------------（ ） A．1.9×104 m B．1.90×104 m C．1.94×103 m D．19000 m 3. 下列各图中，不是．．中心对称图形的是----------------------------------------------（ ） 4. 方程 x2－x＝0 的根是----------------------------------------------------------------------（ ） A．x＝1 B．x＝0 C．x 1＝0, x 2＝1 D．x 1＝0, x 2＝－1 5. 投掷一枚骰子，得到正面朝上的数字是 3 的倍数的概率是---------------------（ ） A. 6 1 B. 2 1 C. 3 2 D. 3 1 6. 面积为 5 的正方形的边长 x 满足不等式-------------------------------------------（ ） A. 1＜x＜2 B. 2＜x＜3 C. 3＜x＜5 D. 5＜x＜25 7.如果反比例函数y＝ x k 的图象经过点（－1，2），那么 k 的值为-------------------（ ） A．－ 2 1 B． 2 1 C．－2 D．2 8. 在△ABC 中，若∠C＝90°，cosA＝ 1 2 ，则∠A 等于-----------------------------（ ） A. 30° B. 45° C. 60° D. 90° 9. ⊙O 的半径为 6，圆心 O 到直线 l 的距离为 5，则直线 l 与⊙O 的位置关系是----（ ） A．相交 B．相切 C．相离 D．无法确定 10. 若一个多边形的每个外角都等于 45°，则它的边数是--------------------------（ ） A. 11 B. 10 C. 9 D. 8 11. 如图，∠MON 内有一点 P ，PP1、PP2 分别被 OM、ON 垂直平分，P1P2 与 OM、ON 分别 交于点 A、B. 若 P1P2＝10 cm，则△PAB 的周长为-----------------------------（ ） A．6 cm B．8 cm C．10 cm D．12 cm 12. 已知 x1 ，x2 是方程 x2－2x－4＝0 的两个根，则代数式 21 11 xx  的值是------（ ） A.－ 2 1 B. 4 1 C. 2 1 D. 4 1 N M P 2 P 1 P B A O 2007年初中毕业生学业模拟考试（一） 第Ⅱ卷（共96分） 二、填空题（每小题3分，共12分） 13．2007 年 4 月 6 日第十一届“西洽会”当天，江苏省已洽谈落实合作项目共 320 个，具体 投资项目情况如图．则科技成果转让项目约有 个（精确到个位）． 14．用配方法将二次函数 y＝2x2－4x＋5化为 y＝a（x－h）2＋k的形式是 ． 15. 某花木场有一块形如等腰梯形 ABCD 的空地（如图），各边的中点分别是 E、F、G、H， 测量得对角线 AC＝10 m，现想用篱笆围成四边形 EFGH 的场地，则篱笆的总长度是 ______________m． 16．如图，若直线 l1 与 l2 相交于点 P，则根据图象可得，二元一次方程组 2 3 3 x y x y      ，的 解是 ． 三、(每小题6分，共24分) 17．计算：－32＋（ 3 －2）0－4sin30°＋ 1)2 1(  ． 18．计算： 1 )11( 2   x x x ． H G F E D C B A 第15题 y＝2x－3 y＝－x＋3 第 13 题 19．如图，将一副三角板按图叠放，则△ADE 与△BCE 相似吗？请说明理由． 20．口袋里有4张卡片，上面分别写了数字1，2，3，4，先抽一张，不放回，再抽一张，“两 张卡片上的数字为一个奇数一个偶数”的概率是多少？ 四、（每小题6分，共12分） 21. 如图，在矩形 ABCD 中，点 E、F 在 BD 上，且 BE＝DF. 求证：四边形 AECF 是平行四边形. 22．如图是某中学在一次社会百科知识竞赛活动中，抽取的一部分同学的测试成绩为样本， 绘制的成绩统计图．请根据该统计图，解答下面问题： （1）本次测试中，抽样的学生有 人； （2）这次测试成绩的众数为 ； （3）若这次测试成绩 90 分以上（含 90 分） 为优秀，则优秀率为 ． 五、（第23题6分，第24题7分，共13分） 23.某气球内充满了一定质量的气体，当温度不变时,气球内气体的气压 p (千帕)是气球体积 A B C D E 30 45 F E D C B A V(米 3) 的反比例函数，其图象如图所示(千帕是一种压强单位). (1)求这个函数的表达式； (2)当气球内的体积为 1.6 米 3 时，气球内的气压是多少千帕? (3)当气球内的气压大于 144 千帕时，气球将爆炸，为了安全起见，气球的体积应不小于多 少米 3 ? 24．如图①，两个全等的直角三角形的直角顶点及一条直角边重合，∠CAO＝30°，OA＝6cm. （1）求OC的长； （2）如图②，将△ACB绕点C逆时针旋转30°到△A′CB′的位置，求点 A 到点 A′所经过的 路径的长. 六、（第25题7分，第26题8分，共15分） C O A' A B' B A O C B 图① 图② 25．我市对城区百条街巷改造工程启动后，甲、乙两个工程队通过公开招标获得某小巷沿街 店面 门头招牌的出新改造.若两个工程队合做，则恰好用 12 天完成任务；若甲、乙合做 9 天后， 由甲再 单独做 5 天也恰好完成.如果每天需要支付甲、乙两公司的工程费用分别为 1.2 万元和 0.7 万 元. 试问：（1）甲、乙两公司单独完成这项工程各需多少天？ （2）要使整个工程费用不超过 22.5 万元，则乙公司最少应施工多少天？ 26. 已知大⊙O的直径 AB＝ a cm，分别以OA、OB为直径作⊙O1和⊙O2，并在⊙O与⊙O1和 ⊙O2的空隙间作两个半径都为 r 的⊙O3和⊙O4，且这些圆互相内切或外切（如图所示）. （1）猜想四边形O1 O4 O2 O3是什么四边形，并说明理由； （2）求四边形O1 O4 O2 O3的面积. 七、（本题8分） 27．如图，直角坐标系中，点 A 的坐标为（1，0），以线段 OA 为边在第一象限内作等边△AOB， 点 C 在 x 的正半轴上，且 OC＞1，连接 BC，以线段 BC 为边在第一象限内作等边△CBD． （1）求证：△OBC≌△ABD； （2）当点 C 沿 x 轴向右移动时，直线 DA 交 y 轴于点 P， 求点 P 坐标． O 4 O 2 O 1 O 3 O B A 八、（本题12分） 28．如图，抛物线 y＝ax2＋bx＋c 的顶点 P 的坐标为（1，－ 3 34 ），交 x 轴于 A、B 两点， 交 y 轴于点 C（0，－ 3 ）． （1）求抛物线的表达式； （2）把△ABC 绕 AB 的中点 E 旋转180 ，得到四边形 ADBC. ① 则点 D 的坐标为 ； ② 试判断四边形 ADBC 的形状，并说明理由． （3）试问在直线 AC 上是否存在一点 F，使得△FBD 的周长最小，若存在，请写出点 F 的坐标；若不存在，请说明理由． 数学试题参考答案及评分标准 第Ⅰ卷（24分） 一、选择题（每小题2分，共24分） 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 D A B C D B C C A D C A 第Ⅱ卷（96分） 二、填空题（每小题3分，共12分） · 13．53 14．y＝2（x－1）2＋3 15. 20 16. 2 1 x y    ， 三、(每小题6分，共24分) 17. 解：原式＝－9＋1－4× 2 1 ＋2 ……………………………………4 分 ＝－8． …………………………………………………6 分 18. 解：原式＝ )1)(1( 1  xx x x x …………………………………4 分 ＝ 1 1 x ． ………………………………………………6 分 19. 解：△ADE∽△BCE．……………………………………………1 分 理由如下： ∵∠DAC＝∠ACB＝90°，∴∠DAC＋∠ACB＝180°．…………2 分 ∴AD∥BC． …………………………………………………3 分 ∴∠DAE＝∠B． ……………………………………………………4 分 又∵∠AED＝∠BEC ． ………………………………………5 分 ∴△ADE∽△BCE．………………………………………………6 分 20. 答：P（两张卡片上的数字为一个奇数一个偶数）＝ 3 2 12 8  ． ………6 分 四、（每小题6分，共12分） 21. 证明： 连接 AC 交 BD 于点 O. ……………………………………………1 分 ∵四边形 ABCD 是矩形， ∴OA＝OC，OB＝OD. …………………………………………………4 分 ∵BE＝DF，∴OE＝OF. …………………………………………………5 分 ∴四边形 AECF 是平行四边形. ……………………………………………6 分 22. （1）50; …………………………………………………………………2 分 （2）90; ……………………………………………………………4分 （3）86%. …………………………………………………………………6 分 五、（第23题6分，第24题7分，共13分） 23. 答：(1)设这个函数的表达式为 p＝ V k .…………………………………1 分 根据图象，得 48＝ 2 k . 解得 k＝96. ………………………………………………………………2 分 ∴ p＝ V 96 ；…………………………………………………………3 分 （2）当 V＝1.6 米 3 时，p＝ 6.1 96 ＝60(千帕)；……………………4 分 （3）由当 p≤144千帕时，得 V 96 ≤144，解得V≥ 3 2 .所以为了安全起见，即气球的体积应 不小于 3 2 米3. ……………………………………………………6分 24．解：（1）在 Rt△AOC 中， ∵∠ACO＝90°，∠CAO＝30°，OA＝6 cm， ∴OC＝ 2 1 OA＝ 2 1 ×6＝3（cm）. ……………………………………2分 （2）在 Rt△AOC 中， ∵∠ACO＝90°，∠CAO＝30°，OA＝6 cm，∴AC＝3 3 （cm）. …………4 分 根据题意，得 ＝ 2 3 180 3330   （cm）. ………………………7分 六、（第25题7分，第26题8分，共15分） 25. 解：（1）设单独完成这项工程甲公司需 x 天，甲公司需 x 1 12 1 1  天.………1 分 根据题意，得 151912 1  x . …………………………………………3 分 解得 x=20. 经检验 x=20 是原方程的解. ……………………………………4 分 答:单独完成这项工程甲公司需 20 天，乙需 30 天. …………………………5 分 （2）设乙公司应施工 y 天. ………………………………………………………6 分 0.7y＋1.2×（1－ 30 y ）÷ 20 1 ≤22.5.………………………………………………7 分 解得 y ≥15. 即乙公司至少要施工 15 天.………………………………………8 分 26. 解：（1）四边形O1 O4 O2 O3为菱形. ……………………………………………1分 理由如下： ∵⊙O、⊙O1、⊙O2、⊙O3、⊙O4互相内切或外切， 又∵⊙O1和⊙O2，⊙O3和⊙O4分别是等圆， ∴O1 O4＝O4 O2＝O2 O3＝O3 O1＝ ra  4 .…………………………………………2分 ∴四边形O1 O4 O2 O3为菱形. ………………………………………………………3分 （2）连接O3 O4 必过点O，且O3 O4⊥AB. ………………………………………4分 ∵⊙O3和⊙O4的半径为 r cm. A B O O 3 O 1 O 2 O 4 又∵⊙O1、⊙O2 的半径为 4 a cm， ∴在Rt△O3 O1 O中，有 222 424                raraa . 解得 r ＝ 6 a . ………………………………………………………………………6分 ∴O3 O＝ 362 aaa  . ∵四边形O1 O4 O2 O3为菱形， ∴S 四边形 O1 O4 O2 O3＝ 632 2aaa  . ……………………………………………………8 分 七、（本题8分） 27. （1）证明：∵OB＝AB，∠OBC＝∠ABD ，BC＝BD，…………………………3 分 ∴△OBC≌△ABD． ………………………………………………………………4 分 （2）由（1）可知∠BAD＝∠BOC＝60°，………………………………………5 分 ∵∠OAP＋∠OAB＋∠BAD＝180°，∴∠OAP＝60°． ………………………6 分 在△OAP 中，∠AOP＝90°，tan∠OAP ＝ OA OP ， ∴OP＝OA·tan60°＝ 3 ． ………………………………………………………7 分∴当点 C 沿 x 轴向右移 动时，求点 P 的坐标为（0，－ 3 ）．…………………8 分 八、（本题12分） 28. 解：（1）抛物线 y＝ 3 34)1(3 3 2 x ．………………………………………3 分 （2）① D（2， 3 ）．……………………………………………………………5 分 ②四边形 ADBC 是矩形． 理由：四边形 ADBC 是平行四边形，且∠ACB＝90°．…………………………7 分 （3）存在．…………………………………………………………………………8 分 作出点 B 关于直线 AC 的对称点 Bˊ，连接 BˊD 与直线 AC 交于点 F． 则点 F 是使△FBD 周长最小的点．………………………………………………10 分 〖方法一〗: ∵∠BˊCA＝∠DAF＝90°，∠BˊFC＝∠DFA， ∴△BˊFC∽△DFA． ∴F 是线段 AC 的中点，求得 F（ 2 1 ， 2 3 ）． ……………………………12 分 〖方法二〗: 求得 Bˊ（－3，－2 3 ）． 直线 BˊD 的表达式为 y＝ 5 3 5 33 x ． 直线 AC 的表达式为 y＝ 33  x ． 两直线的交点 F 为（－ 2 1 ，－ 2 3 ）． …………………………………………12 分 中考数学试题汇编（一次方程（组）） 一、选择题 1、（2007 陕西课改）中国人民银行宣布，从 2007 年 6 月 5 日起，上调人民币存款利率，一 年定期存款利率上调到 3.06%．某人于 2007 年 6 月 5 日存入定期为 1 年的人民币 5000 元（到 期后银行将扣除 20%的利息锐）．设到期后银行应向储户支付现金 x 元，则所列方程正确的 是（ ）C A． 5000 5000 3.06%x    B． 5000 20% 5000 (1 3.06%)x      C． 5000 3.06% 20% 5000 (1 3.06%)x       D． 5000 3.06% 20% 5000 3.06%x      2、（2007 浙江丽水）方程组 5 2 10 x y x y      ，由②  ①，得正确的方程是（ ）B A. 3 10x  B. 5x  C. 3 5x   D. 5x   3、（2007 江苏苏州）方程组 3 7 9 4 7 5 x y x y      的解是 （ ）D A． 2 1 x y     B． 2 3 7 x y    C． 2 3 7 x y    D． 2 3 7 x y   4、（2007 湖南株州）二元一次方程组 3 2 0 x y x y       的解是：（ ） A A. 1 2 x y     B. 1 2 x y     C. 1 2 x y      D. 2 1 x y     5、（2007 山东淄博）若方程组 2 3 13, 3 5 30.9 a b a b      的解是 8.3, 1.2, a b    则方程组 2( 2) 3( 1) 13, 3( 2) 5( 1) 30.9 x y x y          的解是（ ）A （A） 6.3, 2.2 x y    （B） 8.3, 1.2 x y    （C） 10.3, 2.2 x y    （D） 10.3, 0.2 x y    6、（2007 广州）以 1 1 x y     为解的二元一次方程组是（ ）C A． 0 1 x y x y      B． 0 1 x y x y       C． 0 2 x y x y      D． 0 2 x y x y       7、（2007 四川东山）某蔬菜公司收购到某种蔬菜 140 吨，准备加工上市销售．该公司的加 工能力是：每天可以精加工 6 吨或粗加工 16 吨．现计划用 15 天完成加工任务，该公司应按 排几天精加工，几天粗加工？设安排 x 天精加工， y 天粗加工．为解决这个问题，所列方程 组正确的是（ ）D Ａ． 140 16 6 15 x y x y      Ｂ． 140 6 16 15 x y x y      Ｃ． 15 16 6 140 x y x y      Ｄ． 15 6 16 140 x y x y      8、（2007 湖北宜宾）某班共有学生 49 人.一天，该班某男生因事请假，当天的男生人数恰 为女生人数的一半.若设该班男生人数为 x，女生人数为 y，则下列方程组中，能正确计算出 x、y 的是（ ）D A． x–y= 49 y=2(x+1) B． x+y= 49 y=2(x+1) C． x–y= 49 y=2(x–1) D． x+y= 49 y=2(x–1) 9、（2007 浙江舟山）三个同学对问题“若方程组 1 1 1 2 2 2 a x b y c a x b y c      的解是 3 4 x y    ，求方程组 1 1 1 2 2 2 3 2 5 3 2 5 a x b y c a x b y c      的解．”提出各自的想法．甲说：“这个题目好象条件不够，不能求解”； 乙说：“它们的系数有一定的规律，可以试试”；丙说：“能不能把第二个方程组的两个方程 的两边都除以 5，通过换元替代的方法来解决”．参考他们的讨论，你认为这个题目的解应 该是 ． 5 10 x y    二、填空题 1、（2007 湖南湘潭）某市在端年节准备举行划龙舟大赛，预计 15 个队共 330 人参加．已知 每个队一条船，每条船上人数相等，且每条船上有 1 人击鼓，1 人掌舵，其余的人同时划桨．设 每 条 船 上 划 桨 的 有 x 人 ， 那 么 可 列 出 一 元 一 次 方 程 为 ． 答：15（ x ＋2）＝330 2、（2007 湖南怀化）方程组 3 5 2 0 x y x y      的解是 ． 1 2 x y    3、（2007 浙江杭州）三个同学对问题“若方程组 1 1 1 2 2 2 a x b y c a x b y c      的解是 3 4 x y    ，求方程组 1 1 1 2 2 2 3 2 5 3 2 5 a x b y c a x b y c      的解。”提出各自的想法。甲说：“这个题目好象条件不够，不能求解”； 乙说：“它们的系数有一定的规律，可以试试”；丙说：“能不能把第二个方程组的两个方程 的两边都除以 5，通过换元替换的方法来解决”。参考他们的讨论，你认为这个题目的解应 该是 。 5 10 x y    4、（2007 山东青岛）某市在旧城改造过程中，需要整修一段全长 2400m 的道路．为了尽量 减少施工对城市交通所造成的影响，实际工作效率比原计划提高了 20%，结果提前 8 小时完 成任务．求原计划每小时修路的长度．若设原计划每小时修路 x m，则根据题意可得方 程 .   2400 2400 8 1 20%x x    5、（2007 山东济宁）南水北调东线工程已经开工，某施工单位准备对运河一段长 2240m 的 河堤进行加固，由于采用新的加固模式，现计划每天加固的长度比原计划增加了 20m， 因而完成河堤加固工程所需天数将比原计划缩短 2 天，若设现在计划每天加固河堤 xm， 则得方程为 。 2240 20x  － 2240 x ＝2 6、（2007 湖南益阳）某市处理污水，需要铺设一条长为 1000M 的管道，为了尽量减少施工 对交通所造成的影响，实际施工时，每天比原计划多铺设 10 米，结果提前 5 天完成任 务。设原计划每天铺设管道 xm，则可得方程 。 1000 10x  －1000 x ＝5 7、（2007 贵阳）方程 1 2 2x x  的解为 x  ．4 8、（2007 湖南岳阳）分式方程 3 x+4 －1＝0 的解是____________ （答案：x＝－1） 三、解答题 1、（2007 山东青岛）解方程组： 2 5 3 6 x y x y      ， ． 解： 2 5, 3 6. x y x y      ①×3，得 6x＋3y＝15． ③ ②＋③，得 7x＝21， x＝3． …………………………3′ 把 x＝3 代入①，得 2×3＋y＝5，y＝－1． ∴原方程组的解是 3 1 x y     ， ． 2、（2007 浙江金华）解方程组： 5 2 1 x y x y      解： ① ② 得：3 6x  ， 2x  ， 把 2x  代入①得： 3y  ， 2 3. x y   ， 3、（2007 江苏南京）解方程组 4 2 5. x y x y      ， 解：①＋②，得 3 9x  ．解得 3x  ． 把 3x  代入②，得 1y  ． 原方程组的解是 3 1 x y    ， 4、（2007 甘肃陇南）解方程 x(x  1)=2． 有学生给出如下解法： ∵ x(x  1)=2=1×2=（  1）×（  2）， ∴ 1, 1 2; x x     或 2, 1 1; x x     或 1, 1 2; x x       或 2, 1 1. x x       解上面第一、四方程组，无解；解第二、三方程组，得 x=2 或 x=  1． ∴ x=2 或 x=-  1． 请问：这个解法对吗？试说明你的理由． 解：答案一： 对于这个特定的已知方程，解法是对的． 理由是：一元二次方程有根的话，只能有两个根，此学生已经将两个根都求出来了，所 ① ② 以对． 答案二： 解法不严密，方法不具有一般性． 理由是：为何不可以 2=3× 2 3 等，得到其它的方程组？此学生的方法只是巧合了，求对了方 程的根． 5、（2007 江苏连云港）解方程： 1 1 32 2 x x x    ． 解：方程两边同乘 ( 2)x  ，得1 (1 ) 3( 2)x x     ． 解这个方程，得 2x  ． 检验：当 2x  时， 2 0x   ，所以 2x  是增根，原方程无解 6、（2007 湖北孝感）解分式方程： 1 3 2 1 3 2 3 1x x    解：方程两边同乘以 2(3x－1)，去分母， 得 －2－3（3x－1）=4 ………………………………………2 分 解这个整式方程，得 1 3x   ………………………………………4 分 检验：把 1 3x   代入最简公分母 2（3x－1）=2(－1－1)=－4≠0. ∴原方程的解是 1 3x   7．（山东德州）解方程： 1 2 01 1 2 x x x x     ． 解：两边同乘以 ( 1)(1 2 )x x  ， 得 ( 1)(1 2 ) 2 ( 1) 0x x x x     ；································································ 3 分 整理，得5 1 0x   ； 解得 1 5x  ．···························································································5 分 经检验， 1 5x  是原方程的根． 8、（2007 浙江宁波）解方程 2 112 4 x x x    ． 解：方程两边同乘(x-2)(x+2)，得 x(x+2)-(x2-4)=1，……………………2 分 化简，得 2x=-3……………………4 分 x=-3/2，……………………5 分 经检验，x=-3/2 是原方程的根． 9、（2007 安徽芜湖）芜湖供电公司分时电价执行时段分为平、谷两个时段，平段为 8：00~22： 00，14 小时，谷段为 22：00~次日 8：00，10 小时．平段用电价格在原销售电价基础上每 千瓦时上浮 0．03 元，谷段电价在原销售电价基础上每千瓦时下浮 0.25 元，小明家 5 月份 实用平段电量 40 千瓦时， 谷段电量 60 千瓦时，按分时电价付费 42.73 元． (1)问小明该月支付的平段、谷段电价每千瓦时各为多少元? (2)如不使用分时电价结算， 5 月份小明家将多支付电费多少元? 解：(1)设原销售电价为每千瓦时 x 元，根据题意得: ……………………………1 分 40 ( 0.03) 60 ( 0.25) 42.73x x      ………………………………3 分 40 1.2 60 15 42.73x x    100 42.73 13.8x   0.5653x  ． ………………………………4 分 ∴当 0.5653x  时， 0.03 0.5953x   ; 0.25 0.3153x   ． 答:小明家该月支付平段电价为每千瓦时 0.5953 元、谷段电价每千瓦时 0.3153 元．……6 分 (2) 100 0.5653 42.73 13.8   (元) 答:如不使用分时电价结算，小明家 5 月份将多支付 13.8 元． 10、（2007 上海市）2001 年以来，我国曾五次实施药品降价，累计降价的总金额为 269 亿 元，五次药品降价的年份与相应降价金额如表二所示，表中缺失了 2003 年、2007 年相关数 据．已知 2007 年药品降价金额是 2003 年药品降价金额的 6 倍，结合表中信息，求 2003 年 和 2007 年的药品降价金额． 年份 2001 2003 2004 2005 2007 降价金额（亿元） 54 35 40 表二 解：[解法一]设 2003 年和 2007 年的药品降价金额分别为 x 亿元、 y 亿元．················ 1 分 根据题意，得 2 2 6 54 35 40 269 y x x y        ……………………………………………………………… 分 ……………………………………………… 分 解方程组，得 2 2 20 120 x y    ……………………………………………………………………… 分 ……………………………………………………………………… 分 答：2003 年和 2007 年的药品降价金额分别为 20 亿元和 120 亿元．···························1 分 [解法二]设 2003 年的药品降价金额为 x 亿元，·······················································1 分 则 2007 年的药品降价金额为 6x 亿元．································································ 2 分 根据题意，得54 35 40 6 269x x     ．·························································2 分 解方程，得 20x  ， 6 120x  ．····································································· 4 分 答：2003 年和 2007 年的药品降价金额分别为 20 亿元和 120 亿元． 11、（2007 浙江宁波）2007 年 5 月 19 日起，中国人民银行上调存款利率． 人民币存款利率调整表 项 目 调整前年利率％ 调整后年利率％ 活期存款 0.72 0.72 二年期定期存款 2.79 3.06 储户的实得利息收益是扣除利息税后的所得利息，利息税率为 20％． (1)小明于 2007 年 5 月 19 日把 3500 元的压岁钱按一年期定期存入银行，到期时他实得 利息收益是多少元? (2)小明在这次利率调整前有一笔一年期定期存款，到期时按调整前的年利率 2．79％计 息，本金与实得利息收益的和为 2555．8 元，问他这笔存款的本金是多少元? (3)小明爸爸有一张在 2007 年 5 月 19 日前存人的 10000 元的一年期定期存款单，为获 取更大的利息收益，想把这笔存款转存为利率调整后的一年期定期存款．问他是否应该转存? 请说明理由． 约定： ①存款天数按整数天计算，一年按 360 天计算利息． ②比较利息大小是指从首次存入日开始的一年时间内．获得的利息比较．如果不转存， 利息按调整前的一年期定期利率计算；如果转存，转存前已存天数的利息按活期利率计算， 转存后，余下天数的利息按调整后的一年期定期利率计算(转存前后本金不变)． 解：(1)3500×3．06％×80％=85．68(元)， ∴到期时他实得利息收益是 85．68 元．………………………………2 分 (2)设他这笔存款的本金是 x 元， 则 x(1+2．79％×80％)=2555．8，……………………………………4 分 解得 x=2500， ∴这笔存款的本金是 2500 元．……………………………………6 分 (3)设小明爸爸的这笔存款转存前已存了 x 天，由题意得 l0000× 360 x ×0．72％+10000× 360 360 x ×3．06％>10000×2．79％，………………8 分 解得 x<41 7 13 ，……………………9 分 当 他 这 笔 存 款 转 存 前 已 存 天 数 不 超 过 41 天 时 ； 他 应 该 转 存 ； 否 则 不 需 转 存．……………………10 分 12、（2007 恩施自治州）团体购买公园门票票价如下： 购票人数 1～50 51～100 100 人以上 每人门票（元） 13 元 11 元 9 元 今有甲、乙两个旅行团，已知甲团人数少于 50 人，乙团人数不超过 100 人. 若分别购票，两团共计应付门票费 1392 元，若合在一起作为一个团体购票，总计 应付门票费 1080 元． (1)请你判断乙团的人数是否也少于 50 人． (2)求甲、乙两旅行团各有多少人？ 解：（1）∵100×13＝1300<1392 ∴乙团的人数不少于 50 人，不超过 100 人 (2 分) （2）设甲、乙两旅行团分别有 x 人、y 人， (3 分) 则      1080)(9 13921113 yx yx (6 分) 解得：      84 36 y x (7 分) 所以甲、乙两旅行团分别有 36 人、84 人 真题试卷 数 学 试 题 请理解题意，关注约定 注意事项： 1.答卷前考生务必在规定位置将姓名、准考证号等内容填写准确。 2.本试卷分第Ⅰ卷和第Ⅱ卷两部分。第Ⅰ卷为选择题，36 分；第Ⅱ卷为非选择题，84 分，共 120 分。考试时间为 120 分钟。 3.请将第Ⅰ卷选择题答案填写在第Ⅱ卷首答案栏内，填在其它位置不得分。 4.考试结束后，由监考教师把第Ⅰ卷和第Ⅱ卷一并收回。 第Ⅰ卷（选择题 共 36 分） 一、选择题（本大题共 12 小题，在每小题给出的四个选项中，只有一项是正确的，请把正 确的选项填写在答案栏的相应位置上，每小题选对得 3 分，选错、不选或选出的答案超过一 个均记零分，共 36 分） 1. 3 1 的倒数是 A． 3 B． 3 1 C． 3 1 D． 3 2.下列计算结果正确的是 A． 923 )( aa  B． 632 aaa  C． 22)2 1( 21  D． 1)2 160(cos 0  3.在下列四个图案中既是轴对称图形，又是中心对称图形的是 A． B． C． D． 4.2010 年 4 月 20 日晚，“支援青海玉树抗震救灾义演晚会”在莱芜市政府广场成功举行， 热心企业和现场观众踊跃捐款 31083.58 元.将 31083.58 元保留两位有效数字可记为 A．3.1×106 元 B．3.11×104 元 C．3.1×104 元 D．3.10×105 元 5.如图，数轴上 A、B 两点分别对应实数 a、b，则下列结论正确的是 A． 0ab B． 0 ba C． 0 ba D． 0||||  ba 6.右图所示的几何体是由一些小立方块搭成的，则这个几何体的俯视图是 A. B. C. D. 7.已知反比例函数 xy 2 ，下列结论不正确．．．的是 A．图象必经过点(-1,2) B．y 随 x 的增大而增大 C．图象在第二、四象限内 D．若 x＞1，则 y＞-2 10-1a b BA （第 5 题图） （第 6 题图） 8.已知圆锥的底面半径长为 5，侧面展开后得到一个半圆，则该圆锥的母线长为 A．2.5 B．5 C．10 D．15 9.二次函数 cbxaxy  2 的图象如图所示，则一次函数 abxy  的 图象不经过 A．第一象限 B．第二象限 C．第三象限 D．第四象限 10.已知      1 2 y x 是二元一次方程组      1 8 mynx nymx 的解，则 nm 2 的算术平方根为 A．4 B．2 C． 2 D． ±2 11.一个边长为 2 的正多边形的内角和是其外角和的 2 倍，则这个正多边形的半径是 A．2 B． 3 C．1 D．1 2 12.在一次自行车越野赛中，甲乙两名选手行驶的路程 y（千米） 随时间 x（分）变化的图象（全程）如图，根据图象判定下 列结论不正确．．．的是 A．甲先到达终点 B．前 30 分钟，甲在乙的前面 C．第 48 分钟时，两人第一次相遇 D．这次比赛的全程是 28 千米 试卷类型 A 莱芜市 2010 年中等学校招生考试 x （第 9 题图） y O O 14 12 10 96866630 x/分 y/千米 A B C D （第 12 题图） 乙 甲 数 学 试 题 第Ⅱ卷（非选择题 共 84 分） 注意事项： 第 II 卷共 6 页，用钢笔或圆珠笔直接答在本试卷上。 题号 一 二 三 总分 18 19 20 21 22 23 24 分数 第 I 卷选择题答案栏 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 二、填空题（本大题共 5 小题，只要求填写最后结果，每小题填对得 4 分，共 20 分） 13.分解因式：  xxx 23 2 ． 14.有一组数据如下：2，3，a，5，6，它们的平均数是 4，则这组数据的方差是 ． 15.某公司在 2009 年的盈利额为 200 万元，预计 2011年的盈利额将达到 242 万元，若每年 比上一年盈利额增长的百分率相同，那么该公司在 2010 年的盈利额为________万元． 16.在平面直角坐标系中，以点 )3,4(A 、 )0,0(B 、 )0,8(C 为顶点的三角形向上平移 3 个单 位，得到△ 111 CBA （点 111 CBA 、、 分别为点 CBA 、、 的对应点），然后以点 1C 为中 心将△ 111 CBA 顺时针旋转 90 ，得到△ 122 CBA （点 22 BA 、 分别是点 11 BA、 的对应 点），则点 2A 的坐标是 . 17.已知： 321 232 3  C ， 10321 3453 5  C ， 154321 34564 6  C ，…， 观察上面的计算过程，寻找规律并计算 6 10C ． 三、解答题（本大题共 7 小题，共 64 分，解答要写出必要的文字说明、证明过程或推演步 骤） 得分 评卷人 得分 评卷人 18.（本题满分 6 分） 先化简，再求值： 2 4)2 122(   x x xx ，其中 34 x . 19.（本题满分 8 分） 2010 年 5 月 1 日，第 41 届世博会在上海举办，世博知识在校园迅速传 播.小明同学就本班学生对世博知识的了解程度进行了一次调查统计， 下图是他采集数据后绘制的两幅不完整的统计图（A：不了解，B：一般了解，C：了解较多， D：熟悉）.请你根据图中提供的信息解答以下问题： （1）求该班共有多少名学生； （2）在条形统计图中，将表示“一般了解”的部分补充完整； （3）在扇形统计图中，计算出“了解较多”部分所对应的圆心角的度数； （4）从该班中任选一人，其对世博知识的了解程度为“熟悉”的概率是多少？ 得分 评卷人 座 号 A B C D 了解程度 人数 5 10 15 20 25 （第 19 题图） A 10% B 30% D C 20.（本题满分 9 分） 2009 年首届中国国际航空体育节在莱芜雪野举办，期间在市政府广场 进行了热气球飞行表演.如图，有一热气球到达离地面高度为 36 米的 A 处时，仪器显示正前方一高楼顶部 B 的仰角是 37°，底部 C 的俯角是 60°.为了安全飞越高楼， 气球应至少再上升多少米？（结果精确到 0.1 米） （参考数据： ,75.037tan,80.037cos,60.037sin  73.13  ） 21.（本题满分 9 分） 在 Rt△ACB 中，∠C=90°，AC=3cm，BC=4cm，以 BC 为直径作⊙O 交 AB 于点 D. （1）求线段 AD 的长度； （2）点 E 是线段 AC 上的一点，试问当点 E 在什么位置时，直线 ED 与⊙O 相切？请说明理 由. 22.（本题满分 10 分） 为打造“书香校园”，某学校计划用不超过 1900 本科技类书籍和 1620 得分 评卷人 得分 评卷人 得分 评卷人 O D C B A （第 21 题图） B A C （第 20 题图） 本人文类书籍，组建中、小型两类图书角共 30 个.已知组建一个中型图书角需科技类书籍 80 本，人文类书籍 50 本；组建一个小型图书角需科技类书籍 30 本，人文类书籍 60 本． （1）问符合题意的组建方案有几种？请你帮学校设计出来； （2）若组建一个中型图书角的费用是 860 元，组建一个小型图书角的费用是 570 元，试说 明在（1）中哪种方案费用最低？最低费用是多少元？ 23.（本题满分 10 分） 在 ABCD 中，AC、BD 交于点 O，过点 O 作直线 EF、GH，分别交平 行四边形的四条边于 E、G、F、H 四点，连结 EG、GF、FH、HE. 得分 评卷人 （1）如图①，试判断四边形 EGFH 的形状，并说明理由； （2）如图②，当 EF⊥GH 时，四边形 EGFH 的形状是 ； （3）如图③，在（2）的条件下，若 AC=BD，四边形 EGFH 的形状是 ； （4）如图④，在（3）的条件下，若 AC⊥BD，试判断四边形 EGFH 的形状，并说明理由. 24.（本题满分 12 分） 如图，在平面直角坐标系中，已知抛物线 cbxaxy  2 交 x 轴于 得分 评卷人 H G F E O D CB A 图① HG F E O D CB A 图② A B C D O E F G H 图③ A B C D O E F G H 图④ （第 23 题图） )0,6(),0,2( BA 两点，交 y 轴于点 )32,0(C . （1）求此抛物线的解析式； （2）若此抛物线的对称轴与直线 xy 2 交于点 D，作⊙D 与 x 轴相切，⊙D 交 y 轴于点 E、 F 两点，求劣弧 EF 的长； （3）P 为此抛物线在第二象限图像上的一点，PG 垂直于 x 轴，垂足为点 G，试确定 P 点的 位置，使得△PGA 的面积被直线 AC 分为 1︰2 两部分. 数学试题参考答案(A) 评卷说明： 1.选择题和填空题中的每小题，只有满分和零分两个评分档，不给中间分. 2.解答题每小题的解答中所对应的分数，是指考生正确解答到该步骤所对应的累计分数. 本答案对每小题只给出一种或两种解法，对考生的其他解法，请参照评分意见进行评分. 3.如果考生在解答的中间过程出现计算错误，但并没有改变试题的实质和难度，其后续 部分酌情给分，但最多不超过正确解答分数的一半；若出现严重的逻辑错误，后续部分不再 给分. 一、选择题（本大题共 12 个小题，每小题 3 分，共 36 分） 题 号 1 2 3 4 5 6 7 8 9 1 0 1 1 1 2 答 案 A C B C D D B C D B A D 二、填空题（本大题共 5 个小题，每小题 4 分，共 20 分） 13. 2)1(  xx ； 14. 2； 15. 220； 16. )7,11( ； 17.210 三、解答题（本大题共 7 个小题，共 64 分） 18.（本小题满分 6 分） （第 24 题图） x y O A C B D E F 解：原式= 2 4 2 12)2)(2(    x x x xx ………………………1 分 = x x x x    4 2 2 162 ………………………2 分 = )4 2(2 )4)(4(    x x x xx ………………………4 分 = 4 x ………………………5 分 当 34 x 时， 原式= 4)34(  = 434  = 3 ． ………………………6 分 19.（本小题满分 8 分） 解：（1）5÷10％=50（人） ………………………2 分 （2）见右图 ………………………4 分 （3）360°× 50 20 =144° ………………………6 分 （4） 5 1 50 2015550 P ． ………………………8 分 20.（本小题满分 9 分） 解：过 A 作 AD⊥CB，垂足为点 D． ………………………1 分 在 Rt△ADC 中，∵CD=36，∠CAD=60°． ∴AD= 312 3 36 60tan  CD ≈20.76． ……5 分 在 Rt△ADB 中，∵AD≈20.76，∠BAD=37°． ∴BD= 37tanAD ≈20.76×0.75=15.57≈15.6（米）． ………8 分 答：气球应至少再上升 15.6 米． …………………………9 分 21.（本小题满分 9 分） 解：（1）在 Rt△ACB 中，∵AC=3cm，BC=4cm，∠ACB=90°，∴AB=5cm． ……1 分 连结 CD，∵BC 为直径，∴∠ADC =∠BDC =90°． ∵∠A=∠A，∠ADC=∠ACB，∴Rt△ADC ∽Rt△ACB． ∴ AC AD AB AC  ，∴ 5 92  AB ACAD ． …………………………4 分 （2）当点 E 是 AC 的中点时，ED 与⊙O 相切． ………………5 分 证明：连结 OD，∵DE 是 Rt△ADC 的中线． ∴ED=EC，∴∠EDC=∠ECD． ∵OC=OD，∴∠ODC =∠OCD． …………………7 分 ∴∠EDO=∠EDC+∠ODC=∠ECD+∠OCD =∠ACB =90°． ∴ED 与⊙O 相切． …………………………9 分 A B C D 了解程度 人数 5 10 15 20 25 B A C D O D C B A E 22.（本小题满分 10 分） 解：（1）设组建中型图书角 x 个，则组建小型图书角为（30-x）个． ………………1 分 由题意得      1620306050 1900303080 ）（ ）（ xx xx …………………………3 分 解这个不等式组得 18≤x≤20． 由于 x 只能取整数，∴x 的取值是 18，19，20． …………………………5 分 当 x=18 时，30-x=12；当 x=19 时，30-x=11；当 x=20 时，30-x=10． 故有三种组建方案：方案一，组建中型图书角 18 个，小型图书角 12 个；方案二，组建中型 图书角 19 个，小型图书角 11 个；方案三，组建中型图书角 20 个，小型图书角 10 个．…… 7 分 （2）方法一：由于组建一个中型图书角的费用大于组建一个小型图书角的费用，因此组建 中型图书角的数量越少，费用就越低，故方案一费用最低， 最低费用是 860×18+570×12=22320（元）． …………………………10 分 方法二：①方案一的费用是：860×18+570×12=22320（元）； ②方案二的费用是：860×19+570×11=22610（元）； ③方案三的费用是：860×20+570×10=22900（元） 故方案一费用最低，最低费用是 22320 元． …………………………10 分 23.（本小题满分 10 分） 解：（1）四边形 EGFH 是平行四边形． …………………………1 分 证明：∵ ABCD 的对角线 AC、BD 交于点 O． ∴点 O 是 ABCD 的对称中心． ∴EO=FO，GO=HO． ∴四边形 EGFH 是平行四边形． …………………………4 分 （2）菱形． …………………………5 分 （3）菱形． …………………………6 分 （4）四边形 EGFH 是正方形． …………………………7 分 证明：∵AC=BD，∴ ABCD 是矩形． 又∵AC⊥BD， ∴ ABCD 是菱形． ∴ ABCD 是正方形，∴∠BOC=90°，∠GBO=∠FCO=45°．OB=OC． ∵EF⊥GH ，∴∠GOF=90°．∴∠BOG=∠COF． ∴△BOG≌△COF．∴OG=OF，∴GH=EF． …………………………9 分 由（1）知四边形 EGFH 是平行四边形，又∵EF⊥GH，EF=GH. ∴四边形 EGFH 是正方形． …………………………10 分 24. （本小题满分 12 分） 解：（1）∵抛物线 cbxaxy  2 经过点 )0,2(A ， )0,6(B ， )320( ，C ． ∴         32 0636 024 c cba cba ， 解得             32 33 4 6 3 c b a . ∴抛物线的解析式为： 3233 4 6 3 2  xxy . …………………………3 分 （2）易知抛物线的对称轴是 4x .把 x=4 代入 y=2x 得 y=8，∴点 D 的坐标为（4,8）． ∵⊙D 与 x 轴相切，∴⊙D 的半径为 8． …………………………4 分 连结 DE、DF，作 DM⊥y 轴，垂足为点 M． 在 Rt△MFD 中，FD=8，MD=4．∴cos∠MDF= 2 1 ． ∴∠MDF=60°，∴∠EDF=120°． …………………………6 分 ∴劣弧 EF 的长为：  3 168180 120 ． …………………………7 分 （3）设直线 AC 的解析式为 y=kx+b. ∵直线 AC 经过点 )32,0(),0,2( CA . ∴      32 02 b bk ，解得      32 3 b k .∴直线 AC 的解析式为： 323  xy . ………8 分 设点 )0)(3233 4 6 3,( 2  mmmmP ，PG 交直线 AC 于 N， 则点 N 坐标为 )323,(  mm .∵ GNPNSS GNAPNA ::  . ∴①若 PN︰GN=1︰2，则 PG︰GN=3︰2，PG= 2 3 GN. 即 3233 4 6 3 2  mm = ）（ 3232 3  m . 解得：m1=－3， m2=2（舍去）. 当 m=－3 时， 3233 4 6 3 2  mm = 32 15 . ∴此时点 P 的坐标为 )32 15,3( . …………………………10 分 ②若 PN︰GN=2︰1，则 PG︰GN=3︰1， PG=3GN. 即 3233 4 6 3 2  mm = ）（ 3233  m . 解得： 121 m ， 22 m （舍去）.当 121 m 时， 3233 4 6 3 2  mm = 342 . ∴此时点 P 的坐标为 )342,12( . 综上所述，当点 P 坐标为 )32 15,3( 或 )342,12( 时，△PGA 的面积被直线 AC 分成 1︰2 两部分． …………………12 分 x y O A C B D E F P G N M