中考数学三轮真题集训冲刺知识点23相交线与平行线pdf含解析 13页

1 / 13 一、选择题 1．（2019·滨州）如图，AB∥CD，�FGB=154°，FG 平分∠EFD，则∠AEF 的度数等于（ ） A．26° B．52°C．54° D．77° 【答案】B 【解析】∵AB∥CD，∴�DFG+∠FGB=180°．∵�FGB=154°，��DFG=26°．�FG 平分∠EFD， ∴∠EFD=2∠DFG=2×26°=52°．∵AB∥CD，∴∠AEF=∠EFD=52°．故选 B． 2．（2019·苏州）如图．已知直线 a∥b．直线 c 与直线 a、b 分别交于点 A，B 若∠1=54°，则∠2 等于 （ ） A. 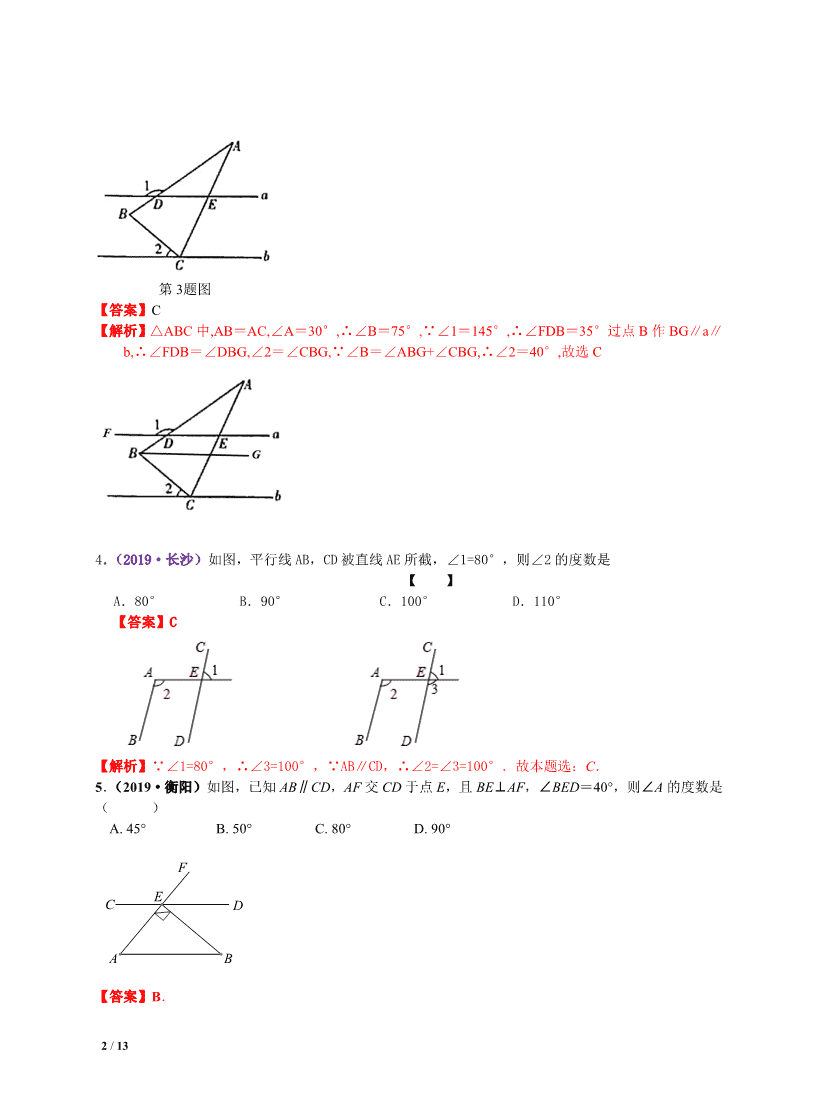126° B.134° C．130° D． 144° （第 4 题） 【答案】A 【解析】本题考查 了 邻补 角 的 性 质 以 及 平 行 线 的 性 质 ，如 图 所 示 ， ∵a∥b， ∠1=54°， ∴ ∠1=∠3=54°， ∴ ∠2=180°-54°=126°．故 选 A． 第 4 题答图 3．（2019·山西）如图,在△ABC 中,AB＝AC,∠A＝30°,直线 a∥b,顶点 C 在直线 b 上,直线 a 交 AB 于 点 D,交 AC 于点 E,若∠1＝145°,则∠2 的度数是( ) A.30° B.35° C.40° D.45° 知识点 23——相交线与平行线 2 / 13 第 3题图 【答案】C 【解析】△ABC 中,AB＝AC,∠A＝30°,∴∠B＝75°,∵∠1＝145°,∴∠FDB＝35°过点 B 作 BG∥a∥ b,∴∠FDB＝∠DBG,∠2＝∠CBG,∵∠B＝∠ABG+∠CBG,∴∠2＝40°,故选 C 4．（2019·长沙）如图，平行线 AB，CD 被直线 AE 所截，∠1=80°，则∠2 的度数是 【 】 A．80° B．90° C．100° D．110° 【答案】C 【解析】∵∠1=80°，∴∠3=100°，∵AB∥CD，∴∠2=∠3=100°．故本题选：C． 5．（2019·衡阳）如图，已知 AB∥CD，AF 交 CD 于点 E，且 BE⊥AF，∠BED＝40°，则∠A 的度数是 （ ） A. 45° B. 50° C. 80° D. 90° 【答案】B． BA E DC F 3 / 13 【解析】�AB∥CD，∴∠B＝∠BED＝40°，∵BE⊥AF，∴∠A＝50°，故选 B． 6．（2019·安徽）如图，在 Rt△ABC 中，∠ACB=90°，BC=12.点 D 在边 BC 上，点 E 在线 段 AD 上，EF⊥AC 于点 F，EG⊥EF 交 AB 于点 G，若 EF=EG，则 CD 的长为（ ） A. 3.6 B. 4 C. 4.8 D. 5 【答案】B 【解析】本题考查了平行线的判定和平行线分线段成比例，解题的关键是作出适当的辅助线和平行线分 线段成比例的性质. 过点 D 作 DH∥CA 交 AB 于点 H，如图.∵EF⊥AC，∠ACB＝90°，∴CD∥EF；∵ EG⊥EF，∴EG∥AC，∴EG∥DH，∴ EF DC ＝ AE AD ＝ EG DH ，又∵EF＝EG，∴CD＝DH.设 CD＝DH＝x， 则 BD＝12－x，由 DH∥CA 得： DH CA ＝ BD BC ，即 6 x ＝12 12 x− ，解得 x＝4，故 CD＝4. 故选 B. 7. （2019·岳阳）如图，已知 BE 平分∠ABC，且 BE∥DC，若∠ABC=50°，则∠C 的度数是（ ） A．20º B．25º C．30º D．50º 【答案】B 【解析】∵BE 平分∠ABC， ∴∠EBC= 1 2 ∠ABC= 1 2 ×50º=25º． ∵BE∥DC， ∴∠C＝∠EBC=25º． 故选 B． 8. （2019·滨州）如图，AB∥CD，∠FGB=154°，FG 平分∠EFD，则∠AEF 的度数等于（ ） H A B C D E F G 4 / 13 A．26° B．52° C．54° D．77° 【答案】B 【解析】∵AB∥CD，∴∠DFG+∠FGB=180°．∵∠FGB=154°，∴∠DFG=26°．∵FG 平分∠EFD， ∴∠EFD=2∠DFG=2×26°=52°．∵AB∥CD，∴∠AEF=∠EFD=52°．故选 B． 9. （2019·济宁）如图，直线 a，b 被直线 c，d 所截，若∠1＝∠2，∠3＝125 °，则∠4 的度数是（ ） A．65° B．60° C．55 ° D．75° 【答案】C 【解析】如图， ∵∠1＝∠2, ∴a∥b, ∴∠3＝∠5＝125°, ∴∠4＝180°－∠5＝180°－125°＝55°, 故选 C． 10. (2019·泰安) 如图,直线 l1∥l2,∠1＝30°,则∠2+∠3＝（ ） A.150° B.180° C.210° D.240° 【答案】C 5 / 13 【解析】过点 A 作 l3∥l1,,∵l1∥l2,∴l2∥l3,∴∠4＝∠1＝30°,∠5+∠3＝180°,∴∠2+∠3＝∠4+∠5+∠3 ＝210°,故选 C. 11.（2019·淄博）如图，小明从 A 处出发沿北偏东 40°方向行走至 B 处，又从点 B 处沿东偏南 20°方 向行走至 C 处，则∠ABC 等于（ ） A．130° B．120° C．110° D．100° 【答案】C． 【解析】如图，由题意，得∠DAB＝40°，∠EBC＝20°， ∵南北方向上的两条直线是平行的， ∴AD∥BF，∴∠ABF＝∠DAB＝40°. 又∵∠EBF＝90°， ∴∠CBF＝90°﹣20°＝70°， ∴∠ABC＝∠ABF＋∠CBF＝40°＋70°＝110°. 故选 C. 12.（2019·乐山）如图，直线 a ∥b ，点 B 在 a 上，且 AB ⊥ BC .若∠1= 35° ，那么∠2 等于（ ） A．45° B．50° C．55° D．60° 6 / 13 【答案】C 【解析】本题考查了平行线的性质，∵ BCAB ⊥ ，∴ ∠ ABC=90° ，∴ ∠3=180°-∠ABC-∠1=55°， ∵直线 a ∥b ，∴ 2∠ =∠3=55°，故选 C. 13.（2019·凉山） 如图，BD∥EF, AE 与 BD 交于点 C，∠B=30°，∠A=75°，则 ∠E 的度数 为 （ ） A. 135° B.125° C. 115° D.105° 【答案】D 【解析】∵∠ACD=∠A+∠B=30°+75°=105°，BD∥EF，∴∠E=∠ACD=105°，故选 D. 14.（2019·攀枝花）如图, AB∥CD, AD＝CD,∠1＝50°，则∠2 的度数是（ ） A．55° B．60° C．65° D．70° 【答案】C 【解析】∵AB∥CD,∴∠ACD＝∠2．∵AD＝CD, ∠1＝50°，∴∠2＝∠CAD＝65°，故选 C． 15.(2019·宁波)已知直线 m∥n,将一块含 45°角的直角三角板 ABC 按如图方式放置,其中斜边 BC 与直 线 n 交于点 D.若∠1＝25°,则∠2 的度数为（ ） A.60° B.65° C.70° D.75° 2 1 C D A B 7 / 13 【答案】C 【解析】∵∠B＝45°,∠1＝25°,∴∠3＝∠1+∠B＝70°,∵m∥n,∴∠2＝∠3＝70°,故选 C. 二、填空题 1．（2019·盐城） 如图，直线 a∥b ，∠1=50°，那么∠2= °. 【答案】50° 【解析】由 a∥b，∠1=50°，根据两直线平行，同位角相等，即可求出∠2 的度数. 2．（2019·淮安）如图，l1 ∥l2 ∥l3 ，直线 a、b 与l1 、l2 、l3 分别相交于点 A、B、C 和点 D、E、F.若 AB=3，DE=2，BC=6，则 EF= . 第 2题图 【答案】4 【解析】∵l1 ∥l2 ∥l3 ，∴ EF DE BC AB = ，又∵AB=3，DE=2，BC=6，∴ EF 2 6 3 = ，∴EF=4. 3．（2019·娄底） 如图（8），AB∥CD，AC∥BD，∠1＝28°，则∠2 的度数为_____________． a b1 2 8 / 13 【答案】28°． 【解析】∵AC∥BD，∠1＝28°， ∴∠A＝∠1＝28°． 又∵AB∥CD， ∴∠2＝∠A＝28°． 4．（2019·黄冈）如图，直线AB∥CD，直线EC分别与AB，CD相交于点A，点C.AD平分∠BAC，已 知∠ACD＝80°，则∠DAC的度数为 . 【答案】50° 【解析】�AB�CD，�ACD＝80°，�BAC＝180°-�ACD＝180°-80°＝100°，又因为 AD 平分∠BAC，所 以∠BAC＝ 1 2 �BAC＝ 1 2 ×100°＝50°. 5.（2019·自贡）如图，直线 AB、CD 被直线 EF 所截，AB∥CD，∠1=120°，则∠2= . 【答案】60° 【解析】CD 与 EF 交于 G， ∵AB∥CD， ∴∠EGC=∠1=120°， ∵∠EGC 与∠2 是邻补角， ∴∠2=1800-∠EGC=600， 三、解答题 1．（2019·武汉）如图，点 A、B、C、D 在一条直线上，CE 与 BF 交于点 G，∠A＝∠1，CE∥DF，求证： ∠E＝∠F 9 / 13 证明：∵∠A＝∠1， ∴AE∥BF， ∴∠E＝∠2． ∵CE∥DF， ∴∠F＝∠2． ∴∠E＝∠F． 2．（2019·滨州）如图，在平面直角坐标系中，菱形 OABC 的边 OA 在 x 轴的正半轴上，反比例函数 y ＝ k x （x＞0）的图象经过对角线 OB 的中点 D 和顶点 C．若菱形 OABC 的面积为 12，则 k 的值为 （ ） A．6 B．5 C．4 D．3 【答案】C 【解析】如图，连接 AC，∵四边形 OABC 是菱形，∴AC 经过点 D，且 D 是 AC 的中点．设点 A 的坐 标为（a，0）， 点 C 坐标为（b，c）， 则 点 D 坐标为（ 2 ab+ ， 2 c ）． ∵ 点 C 和点 D 都在反比例函数 y= k x 的图象上，�bc= 2 ab+ × 2 c ，∴ a=3b；∵菱形的面积为 12，∴ ac=12，∴ 3bc=12，bc=4，即 k=4．故 选 C． 10 / 13 法 2：设点 A 的坐标为（a，0）， 点 C 的坐标为（c， ）， 则 ，点 D 的坐标为（ ）， ∴ ，解得，k＝4，故选 C． 3．（2019·德州）如图，点 A1、A3、A5…在反比例函数 y＝ （x＞0）的图象上，点 A2、A4、A6…… 在反比例函数 y＝ （x＞0）的图象上，∠OA1A2＝∠A1A2A3＝∠A2A3A4＝…＝∠ α ＝60°，且 OA1 ＝2，则 An（n 为正整数）的纵坐标为 ．（用含 n 的式子表示） 【答案】（﹣1）n+1 （ ） 【解析】过 A1 作 A1D1⊥x 轴于 D1，∵OA1＝2，∠OA1A2＝∠ α ＝60°，∴△OA1E 是等边三角形， ∴A1（1， ）， ∴ k＝ ，∴y＝ 和 y＝﹣ ，过 A2 作 A2D2⊥x 轴于 D2，∵∠A2EF＝∠A1A2A3 ＝60°， 11 / 13 ∴△A2EF 是等边三角形，设 A2（x，﹣ ）， 则 A2D2＝ ，Rt△EA2D2 中 ，∠ EA2D2＝30° ，∴ ED2 ＝ ， ∵OD2＝2+ ＝x，解得：x1＝1﹣ （ 舍 ）， x2＝1+ ，∴EF＝ ＝ ＝ ＝2 （ ﹣1）＝2 ﹣2，A2D2＝ ＝ ＝ ，即 A2 的纵坐标为﹣ ；过 A3 作 A3D3⊥x 轴于 D3， 同理得：△A3FG 是等边三角形，设 A3（x， ）， 则 A3D3＝ ，Rt△FA 3D3 中，∠FA 3D3＝30°， ∴FD3＝ ，∵ OD3＝2+2 ﹣2+ ＝x，解得：x1＝ （舍），x2＝ + ；∴ GF＝ ＝ ＝2（ ﹣ ）＝2 ﹣2 ，A3D3＝ ＝ ＝ （ ﹣ ）， 即 A3 的纵坐标为 （ ﹣ ）； … ∴ An（n 为正整数）的纵坐标为：（﹣1）n+1 （ ）；故答案为：（﹣1）n+1 （ ）． 4. （2019·遂宁）如图，一次函数 y=x-3 的图像与反比例函数 = (k ≠ 0） x ky 的图像交于点 A 与点 B(a,-4), (1) 求反比例函数的表达式； （2）若动点 P 是第一象限内双曲线上的点（不与点 A 重合 0，连接 OP，且过点 P 作 y 轴的平行线交直 线 AB 于点 C，连接 OC，若△POC 的面积为 3，求出点 P 的坐标. 解 ：（ 1）∵B(a,-4)在一次函数 y=x-3 上， 12 / 13 ∴a=-1, ∴B(-1，-4), ∵B(-1，-4)在反比例函数图像上， ∴k=(-1)(-4）=4 ∴反比例函数表达式为 xy 4= （2）如图，设 P（m, m 4 )， 则 C( m 4 +3, m 4 )， ∴PC= m 4 +3-m,OH= m 4 , ∵△POC 的面积为 3， ∴ 34)-34 2 1 =×+ mmm （ ∴m1=2, 5 4 2 −=m ∵P 点在第一象限， ∴ 5 4 2 −=m 不合题意舍去， ∴m=2 ∴P(2,2) 5．(2019·广元)如图,在平面直角坐标系中,直线 AB 与 y 轴交于点 B(0,7),与反比例函数 y＝ 8 x − 在第二 象限内的图象相交于点 A(－1,a). (1)求直线 AB 的解析式; (2)将直线 AB 向下平移 9 个单位后与反比例函数的图象交于点 C 和点 E,与 y 轴交于点 D,求△ACD 的面 积; (3)设直线 CD 的解析式为 y＝mx+n,根据图象直接写出不等式 mx+n≤ 8 x − 的解集. 13 / 13 第 5 题图 解：(1)∵点 A(－1,a)在反比例函数 y＝ 8 x − 图象上,∴a＝ 8 1 − − ,∴a＝8,∴A(－1,8),设直线 AB 的解析式为 y ＝kx+b,则 8= 7 kb b −+  = ,∴ 1 7 k b = −  = ,∴y＝－x+7; (2)将直线 AB 向下平移 9 个单位后,得到直线 CD:y＝－x－2,∴D(0,－2),令 8 x − ＝－x－2,得 x1＝2,x2＝－4, 当 x＝2 时,y＝－4,∴E(2,－4),当 x＝－4 时,y＝2,∴C(－4,2),过点 A 作 y 轴的平行线,交 DC 与点 M, 则点 D 坐标为(－1,－1),∴S△ACD＝S△ACM+S△ADM＝18; (3)∵C(－4,2),E(2,－4),∴不等式 mx+n≤ 8 x − 的解集为－4≤x<0,x≥2. M