中考数学三轮真题集训冲刺知识点24线段垂直平分线角平分线中位线pdf含解析 3页

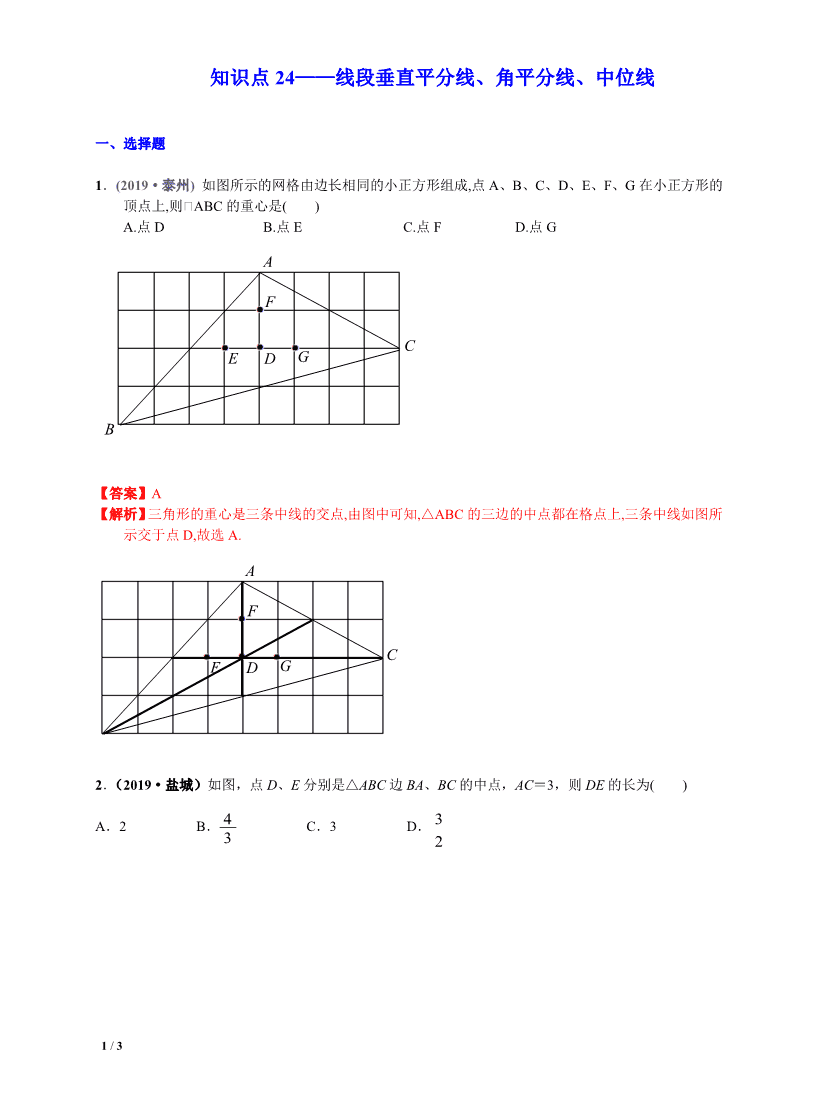
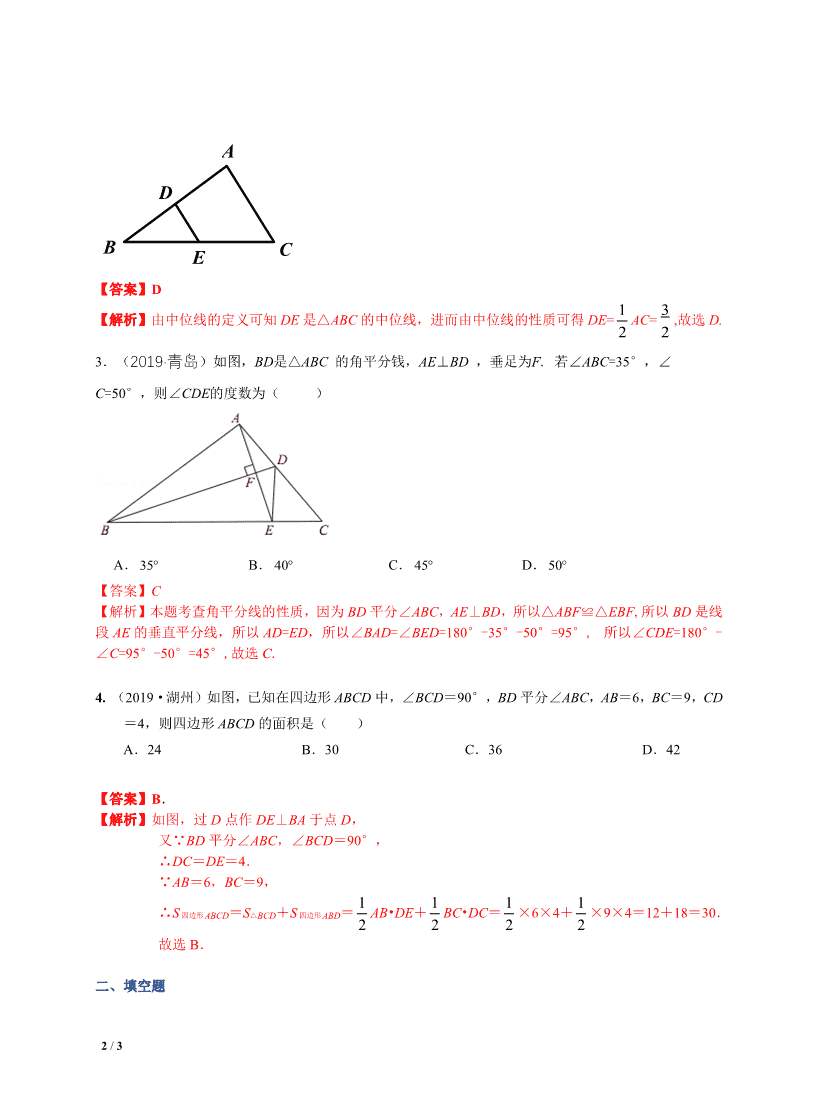
1 / 3 一、选择题 1．(2019·泰州) 如图所示的网格由边长相同的小正方形组成,点 A、B、C、D、E、F、G 在小正方形的 顶点上,则�ABC 的重心是( ) A.点 D B.点 E C.点 F D.点 G 【答案】A 【解析】三角形的重心是三条中线的交点,由图中可知,△ABC 的三边的中点都在格点上,三条中线如图所 示交于点 D,故选 A. 4 2．（2019·盐城）如图，点 D、E 分别是△ABC 边 BA、BC 的中点，AC＝3，则 DE 的长为( ) A．2 B． C．3 D． 3 2 3 A B C E D G F A C E D G F 知识点 24——线段垂直平分线、角平分线、中位线 2 / 3 【答案】D 【解析】由中位线的定义可知 DE 是△ABC 的中位线，进而由中位线的性质可得 DE= 2 1 AC= 2 3 ,故选 D. 3．（2019·青岛）如图，BD是△ABC 的角平分钱，AE⊥BD ，垂足为F. 若∠ABC=35°，∠ C=50°，则∠CDE的度数为（ ） A．35° B． 40° C． 45° D．50° 【答案】C 【解析】本题考查角平分线的性质，因为 BD 平分∠ABC，AE⊥BD，所以△ABF≌△EBF,所以 BD 是线 段 AE 的垂直平分线，所以 AD=ED，所以∠BAD=∠BED=180°-35°-50°=95°, 所以∠CDE=180°- ∠C=95°-50°=45°,故选 C. 4. （2019·湖州）如图，已知在四边形 ABCD 中，∠BCD＝90°，BD 平分∠ABC，AB＝6，BC＝9，CD ＝4，则四边形 ABCD 的面积是（ ） A．24 B．30 C．36 D．42 【答案】B． 【解析】如图，过 D 点作 DE⊥BA 于点 D， 又∵BD 平分∠ABC，∠BCD＝90°， ∴DC＝DE＝4． ∵AB＝6，BC＝9， ∴S 四边形 ABCD＝S△BCD＋S 四边形 ABD＝ 1 2 AB•DE＋ 1 2 BC•DC＝ 1 2 ×6×4＋ 1 2 ×9×4＝12＋18＝30． 故选 B． 二、填空题 E D B A C 3 / 3 1．（2019·长沙）如图，要测量池塘两岸相对的 A，B 两点间的距离，可以在池塘外选一点 C，连接 AC， BC，分别取 AC，BC 的中点 D，E，测得 DE=50m，则 AB 的长是 m． 【答案】100 【解析】∵AC，BC 的中点 D，E，∴DE 是△ABC 的中位线，∴DE= 1 2 AB. ∵DE=50m，∴AB=100m. 故填： 100． 2．(2019·广元)如图,已知:在△ABC 中,∠BAC＝90°,延长 BA 到点 D,使 AD＝ 1 2 AB,点 E,F 分别是边 BC,AC 的中点. 求证:DF＝BE. 解：连接 AE,∵点 E,F 分别是边 BC,AC 的中点,∴EF 是△ABC 的中位线,∴EF∥AB,即 EF∥AD,且 EF＝ 1 2 AB,又∵AD＝ 1 2 AB,∴AD＝EF,∴四边形 ADFE 是平行四边形,∴DF＝AE,又∵在 Rt△ABC 中,点 E 是中点,∴AE＝ 1 2 BC＝BE＝CE,∴BE＝DF.