人教版九年级下册数学单元测试题（第26章） 16页

人教版九年级下册数学单元测试题（第26章）‎ ‎(考试时间：120分钟　满分：120分)‎ 分数：____________　‎ 一、选择题(本大题共6小题，每小题3分，共18分，每小题只有一个正确选项)‎ ‎1．下列函数中，y是x的反比例函数的是 (　B　)‎ A．y＝－ B．y＝ C．y＝5x D．y＝－x2‎ ‎2．已知反比例函数y＝(k≠0)的图象经过点M(－2，2)，则k的值是 (　A　)‎ A．－4 B．－1 C．1 D．4‎ ‎3．直线y＝－x＋b与反比例函数y＝的图象的一个交点为A(－1，2)，则另一个交点B的坐标为 (　D　)‎ A．(－2，1) B．(2，1) C．(1，－2) D．(2，－1)‎ ‎4．当温度不变时，气球内气体的气压p(单位：kPa)是气体体积V(单位：m3)的函数，下表记录了一组实验数据：p与V的函数关系式可能是 (　D　)‎ V(单位：m3)‎ ‎1‎ ‎1.5‎ ‎2‎ ‎2.5‎ ‎3‎ p(单位：kPa)‎ ‎96‎ ‎64‎ ‎48‎ ‎38.4‎ ‎32‎ A.p＝96V B．p＝－16V＋112‎ C．p＝16V2－96V＋176 D．p＝ ‎5．如图，点A是反比例函数y＝(x＞0)的图象上任意一点，AB∥x轴交反比例函数y＝－的图象于点B，以AB为边作平行四边形ABCD，其中C，D在x轴上，则S▱ABCD的值为 (　D　)‎ A.2 B．3 C．4 D．5‎ ‎6．★已知点A在函数y1＝－(x>0)的图象上，点B在直线y2＝kx＋1＋k(k为常数且k≥0)上，若A，B两点关于原点对称，则称点A，B为函数y1，y2图象上的一对“友好点”．请问这两个函数图象上的“友好点”对数的情况为 (　A　)‎ A．有1对或2对 B．只有1对 C．只有2对 D．有2对或3对 二、填空题(本大题共6小题，每小题3分，共18分)‎ ‎7．反比例函数y＝(m－2)x2m＋1的函数值为，自变量x的值是__－9‎ ‎__．‎ ‎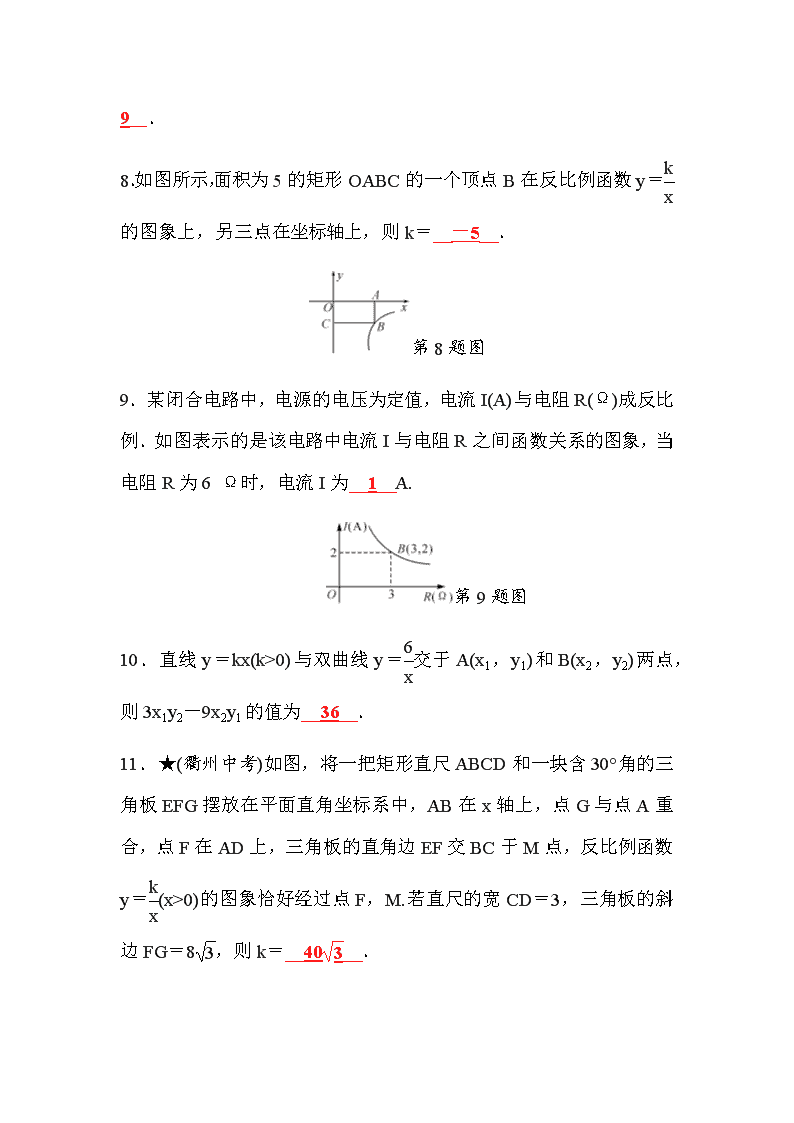8．如图所示，面积为5的矩形OABC的一个顶点B在反比例函数y＝的图象上，另三点在坐标轴上，则k＝__－5__．‎ 第8题图 ‎9．某闭合电路中，电源的电压为定值，电流I(A)与电阻R(Ω)成反比例．如图表示的是该电路中电流I与电阻R之间函数关系的图象，当电阻R为6 Ω时，电流I为__1__A.‎ ‎ 第9题图 ‎10．直线y＝kx(k>0)与双曲线y＝交于A(x1，y1)和B(x2，y2)两点，则3x1y2－9x2y1的值为__36__．‎ ‎11．★(衢州中考)如图，将一把矩形直尺ABCD和一块含30°角的三角板EFG摆放在平面直角坐标系中，AB在x轴上，点G与点A重合，点F在AD上，三角板的直角边EF交BC于M点，反比例函数y＝(x>0)的图象恰好经过点F，M.若直尺的宽CD＝3，三角板的斜边FG＝8，则k＝__40__．‎ 第11题图 ‎12．★如图，▱ABOD的顶点A(0，3)，B(－2，0)，点D在反比例函数的图象上．若OD＝OP，且点P在该函数图象上，则满足条件的点P的坐标为__(3，2)，(－2，－3)，(－3，－2)__.‎ ‎ 第12题图 三、(本大题共5小题，每小题6分，共30分)‎ ‎13．(1)若反比例函数y＝的图象在同一象限内满足y随x的增大而减小，求m的取值范围；‎ ‎(2)某种大米单价是y元/千克，若购买x千克花费了75元，求y与x之间的关系式．‎ 解：(1)依题意得m－3>0，得m>3.‎ ‎(2)y＝(x≥0).‎ ‎14．已知y＝(5m－3)x2－n＋(m＋n).‎ ‎(1)当m，n为何值时，此函数为一次函数？‎ ‎(2)当m，n为何值时，此函数为反比例函数？‎ 解：(1)当m≠，n＝1时，此函数为一次函数．‎ ‎(2)当m＝－3，n＝3时，此函数为反比例函数．‎ ‎15．已知y是x的反比例函数，下表列出了x与y的一些对应值．‎ x ‎…‎ ‎－4‎ ‎－3‎ ‎－2‎ ‎－1‎ ‎…‎ y ‎…‎ ‎6‎ ‎…‎ ‎(1)求出这个反比例函数的解析式；‎ ‎(2)根据反比例函数的解析式补全上表．‎ 解：(1)这个反比例函数的解析式为y＝－.‎ ‎(2)表格中填：－5　9　18.‎ ‎16．已知反比例函数y＝，点A(m，y1)，B(m＋2，y2)是函数图象上两点，且满足＝－，求k的值．‎ 解：∵点A(m，y1)，B(m＋2，y2)是函数y＝图象上的两点，‎ ‎∴y1＝，y2＝，‎ ‎∴＝，＝.‎ ‎∵＝－，∴＝－，‎ 解得k＝4.‎ 经检验，k＝4是此方程的根，∴k＝4.‎ ‎17．已知反比例函数y＝(k为常数，k≠0)的图象经过点A(2，3).‎ ‎(1)求这个函数的解析式；‎ ‎(2)判断点B(－1，6)，C(3，2)是否在这个函数的图象上，并说明理由；‎ ‎(3)当－1＜x＜2且x≠0时，求y的取值范围．‎ 解：(1)把点A的坐标(2，3)代入解析式，得3＝，解得k＝6.‎ ‎∴这个函数的解析式为y＝.‎ (2) 点B不在这个函数的图象上，点C在这个函数的图象上．‎ 理由：当x＝－1时，y＝＝－6；‎ 当x＝3时，y＝＝2，‎ ‎∴点B不在这个函数的图象上，点C在这个函数的图象上．‎ (3) 当x＝－1时，y＝－6，‎ 当－13，‎ ‎∴当－13.‎ 四、(本大题共3小题，每小题8分，共24分)‎ ‎18．如图，一次函数y＝kx＋b与反比例函数y＝(x>0)的图象交于A(m，6)，B(3，n)两点．‎ ‎(1)求一次函数的解析式；‎ ‎(2)根据图象直接写出kx＋b－<0的x的取值范围．‎ 解：(1)分别把A(m，6)，B(3，n)代入y＝(x>0)，‎ 得6m＝6，3n＝6，解得 m＝1，n＝2，所以点A的坐标为(1，6)，点B的坐标为(3，2).‎ 分别把A(1，6)，B(3，2)代入y＝kx＋b，得 解得所以一次函数的解析式为y＝－2x＋8.‎ ‎(2)当03时，kx＋b－<0.‎ ‎19．如图，在▱OABC中，OA＝2，∠AOC＝45°，点C在y轴上，点D是BC的中点，反比例函数y＝(x＞0)的图象经过点A，D.‎ ‎(1)求k的值；(2)求点D的坐标．‎ 解：(1)∵OA＝2，∠AOC＝45°，‎ ‎∴A(2，2)，‎ ‎∴k＝4.‎ ‎(2)四边形OABC是平行四边形OABC，‎ ‎∴AB⊥x轴，‎ ‎∴B的横坐标为2.‎ ‎∵点D是BC的中点，∴D点的横坐标为1，‎ ‎∴D(1，4).‎ ‎20．如图，在平面直角坐标系中，一次函数y1＝kx＋b(k≠0)的图象与反比例函数y2＝(m≠0)的图象相交于第一、三象限内的A(3，5)，B(a，－3)两点，与x轴交于点C.‎ ‎(1)求该反比例函数和一次函数的解析式；‎ 解：把A(3，5)代入y2＝(m≠0)，‎ 可得m＝3×5＝15，‎ ‎∴反比例函数的解析式为y2＝；‎ 把点B(a，－3)代入y2＝，可得a＝－5，‎ ‎∴B(－5，－3).‎ 把A(3，5)，B(－5，－3)代入y1＝kx＋b，可得 解得 ‎∴一次函数的解析式为y1＝x＋2.‎ ‎(2)在y轴上找一点P使PB－PC最大，求PB－PC的最大值及点P的坐标．‎ 解：一次函数的解析式为y1＝x＋2，令x＝0，则y＝2，‎ ‎∴一次函数与y轴的交点为P(0，2)，‎ 此时PB－PC＝BC最大，点P即为所求．‎ 令y＝0，则x＝－2，∴C(－2，0)，‎ ‎∴BC＝＝3.‎ ‎∴PB－PC的最大值是3，点P的坐标是(0，2).‎ 五、(本大题共2小题，每小题9分，共18分)‎ ‎21．(宜宾中考)如图，一次函数y＝kx＋b的图象与反比例函数y＝(x<0)的图象相交于点A(－3，n)，B(－1，－3)两点，与x轴，y轴分别交于点P，Q，过点A作AC⊥OP于点C.‎ ‎(1)求一次函数和反比例函数的解析式；‎ ‎(2)求四边形ABOC的面积．‎ 解：(1)将B(－1，－3)代入y＝中，‎ 有－3＝，‎ ‎∴m＝3.‎ ‎∴反比例函数的解析式为y＝.‎ 将A(－3，n)代入y＝中，有n＝＝－1.‎ 将A(－3，－1)，B(－1，－3)代入y＝kx＋b得 解得 ‎∴一次函数的解析式为y＝－x－4.‎ ‎(2)过点B作BE⊥y轴于点E.‎ ‎∵y＝－x－4，∴Q(0，－4).‎ ‎∴S四边形ABOC＝S四边形ACOQ－S△OBQ ‎＝(AC＋OQ)·OC－OQ·BE ‎＝×(1＋4)×3－×4×1＝.‎ 答：四边形ABOC的面积为.‎ ‎22．某中学为了预防新冠肺炎，对教室采用药熏消毒法进行消毒，已知药物燃烧时，室内每立方米空气中的含药量y(mg)与时间x(min)成正比例．药物燃烧后，y与x成反比例(如图所示)，现测得药物6 min燃毕，此时室内空气中每立方米的含药量为4 mg.‎ ‎(1)写出药物燃烧前后，y关于x的函数关系式；‎ ‎(2)研究表明，当空气中每立方米的含药量低于1.6 mg 时学生方可进教室，那么从消毒开始，至少需要经过多少分钟，学生方能回到教室？‎ ‎(3)研究表明，当空气中每立方米的含药量不低于2 mg且持续时间不低于9 min时，才能有效杀灭空气中的病菌，那么此次消毒是否有效？‎ 解：(1)设药物燃烧时y关于x的函数关系式为y＝k1x(k1＞0)，‎ 代入(6，4)得4＝6k1，‎ ‎∴k1＝.‎ 设药物燃烧后y关于x的函数关系式为y＝(k2＞0)，‎ 代入(6，4)得4＝，‎ ‎∴k2＝24，‎ ‎∴药物燃烧时y关于x的函数关系式为y＝x(0≤x≤6)，‎ 药物燃烧后y关于x的函数关系式为y＝(x＞6).‎ (2) 令y＝中y≤1.6，得x≥15，即从消毒开始，‎ 至少需要15分钟后学生才能进入教室．‎ ‎(3)把y＝2代入y＝x，得x＝3.‎ 把y＝2代入y＝，得x＝12.‎ ‎∵12－3＝9，‎ ‎∴这次消毒是有效的．‎ 六、(本大题共12分)‎ ‎23．如图，在平面直角坐标系xOy中，函数y＝－x＋b的图象与函数y＝(x＜0)的图象相交于点A(－1，6)，并与x轴交于点C，点D是线段AC上一点，△ODC与△OAC的面积比为2 ∶3.‎ ‎(1)k＝__－6__，b＝__5__；‎ ‎(2)求点D的坐标；‎ ‎(3)若将△ODC绕点O逆时针旋转，得到△OD′C′，其中点D′落在x轴负半轴上，判断点C′是否落在函数y＝(x＜0)的图象上，并说明理由．‎ 解：(2)如图①，过点D作DM⊥x轴，垂足为M，‎ 过点A作AN⊥x轴，垂足为N，‎ ‎∵＝＝，∴＝.‎ 又∵点A的坐标为(－1，6)，∴AN＝6，‎ ‎∴DM＝4，即点D的纵坐标为4.‎ 把y＝4代入y＝－x＋5中，得x＝1，∴D(1，4).‎ (2) 点C′不在函数y＝(x<0)的图象上．‎ 理由：由题意可知，OD′＝OD＝＝，‎ 如图②，过点C′作C′G⊥x轴，垂足为G.‎ ‎∵S△ODC＝S△OD′C′，∴OC·DM＝OD′·C′G，‎ 即5×4＝C′G，∴C′G＝.‎ 在Rt△OC′G中，∵OG＝＝＝，‎ ‎∴C′的坐标为.‎ ‎∵×≠－6，∴点C′不在函数y＝－的图象上．‎