第1章 第2节 简单的变速直线运动-2021年初中物理竞赛及自主招生大揭秘专题突破 7页

第二节 简单的变速直线运动 如果物体沿着一条直线运动，并且速度的大小不恒定，那么物体的运动就是变速直线运动。折 返运动实际上也是变速直线运动，因为速度的方向发生了变化。 一、变速直线运动的平均速度 如果某物体在一段时间内运动的路程恰与一个匀速直线运动在相等时间内通过的路程相等，我 们就说这个匀速直线运动的速度是该物体在这段时间内的平均速度，这里实际是用匀速直线运动的 速度来表示该物体在某段时间内运动的平均快慢程度，体现了一种等效代替的思想。 平均速度用符号v 来表示，其定义式为 sv t  ，应注意的是： (1)在任何时间段，匀速直线运动的平均速度均为定值。 (2)变速运动的平均速度往往与选取的时间段有关，选取的时间段不同，平均速度可能不同。 例1 小明的家与学校之间有一座山，每天上学的过程中，有五分之二的路程是上坡路，其余是 下坡路。小明从家到学校要走36min ，如果小明上坡行走速度不变，下坡行走速度也不变，而且上 坡行走速度是下坡行走速度的三分之二，求： (1)小明上学过程与放学过程平均速度之比； (2)小明放学回家所需的时间。 分析与解 (1)由题意，设小明上学过程中上坡路为 2s ，则下坡路为3s ；再设上坡速为 2v ，则 下坡速度为 3v 。于是小明上学的平均速度为 5 5 2 3 2 2 3 sv vs s v v    上学 ；放学时，原来的下坡路变为上 坡路，原来的上坡路变为下坡路，因此放学时的平均速度为 5 30 3 2 13 2 3 s vs s v v   ，因此上学、放学的平 均速度之比为 13=12 v v 上学 放学 。 (2)由于上学、放学所行走的路程相同，根据 st v  可知，行走时间与平均速度成反比，因此有 13=12 t v t v  上学放学 放学上学 ，可知放学行走时间为 39mint 放学 。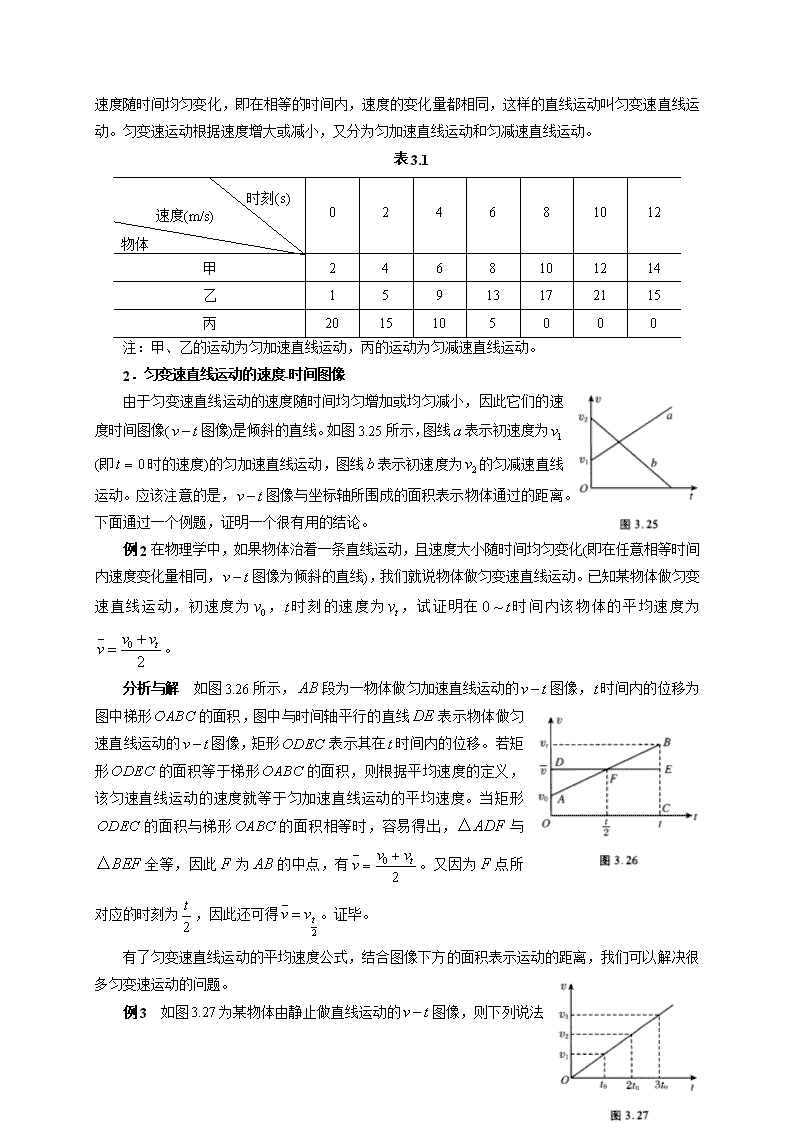 二、匀变速直线运动 1．匀变速直线运动的概念 表3.1中给出了做直线运动的3个物体的速度与时间的关系，由表可知甲、乙两物体加速，丙物 体减速。每经过 2s 时间，甲物体速度都增加 2m / s ；每经过 2s 时间，乙物体速度都增加 4m / s ； 每经过 2s 时间，丙物体速度都减小5m / s ，直至速度减为零最后静止。这3个物体在运动过程中， 速度随时间均匀变化，即在相等的时间内，速度的变化量都相同，这样的直线运动叫匀变速直线运 动。匀变速运动根据速度增大或减小，又分为匀加速直线运动和匀减速直线运动。 表 3.1 时刻(s) 速度(m/s) 物体 0 2 4 6 8 10 12 甲 2 4 6 8 10 12 14 乙 1 5 9 13 17 21 15 丙 20 15 10 5 0 0 0 注：甲、乙的运动为匀加速直线运动，丙的运动为匀减速直线运动。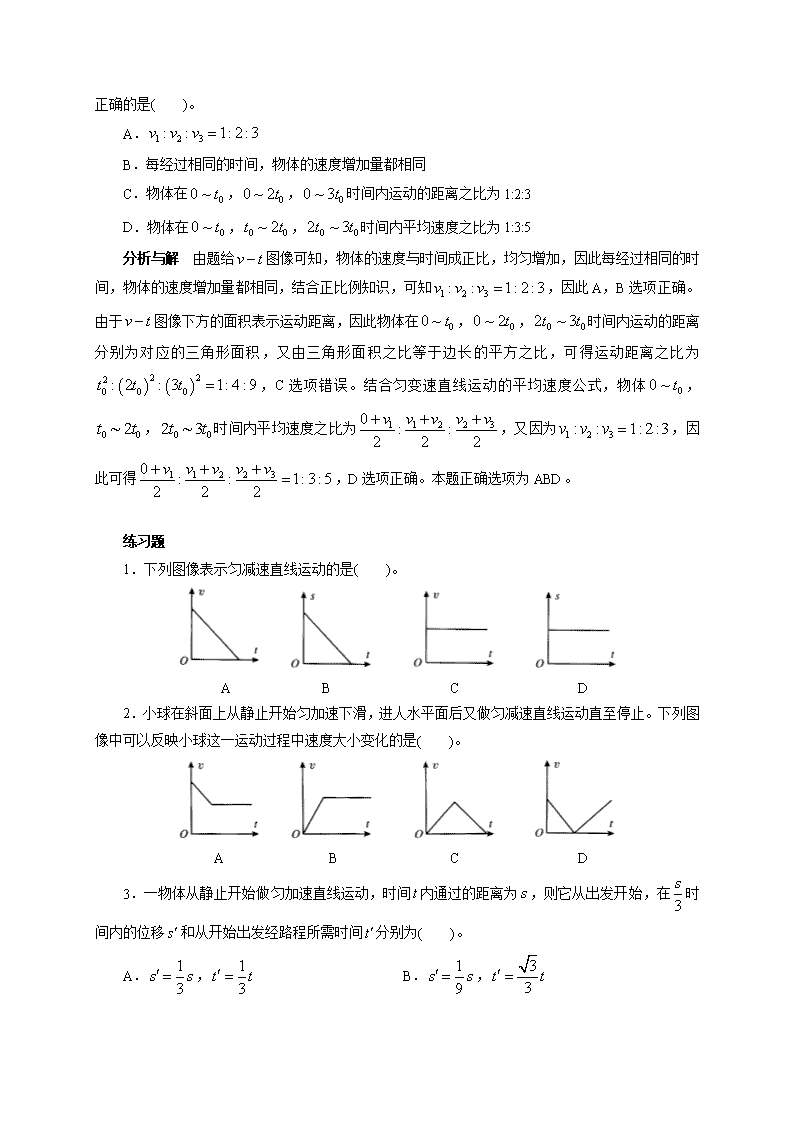 2．匀变速直线运动的速度-时间图像 由于匀变速直线运动的速度随时间均匀增加或均匀减小，因此它们的速 度时间图像( v t 图像)是倾斜的直线。如图 3.25 所示，图线 a 表示初速度为 1v (即 0t  时的速度)的匀加速直线运动，图线b 表示初速度为 2v 的匀减速直 线运动。应该注意的是， v t 图像与坐标轴所围成的面积表示物体通过的距 离。下面通过一个例题，证明一个很有用的结论。 例 2 在物理学中，如果物体治着一条直线运动，且速度大小随时间均匀变化(即在任意相等时间 内速度变化量相同，v t 图像为倾斜的直线)，我们就说物体做匀变速直线运动。已知某物体做匀变 速直线运动，初速度为 0v ，t 时刻的速度为 tv ，试证明在 0 ~ t 时间内该物体的平均速度为 0 2 tv vv  。 分析与解 如图 3.26 所示， AB 段为一物体做匀加速直线运动的 v t 图像，t 时间内的位移为 图中梯形 OABC 的面积，图中与时间轴平行的直线 DE 表示物体做匀 速直线运动的 v t 图像，矩形ODEC 表示其在t 时间内的位移。若矩 形ODEC 的面积等于梯形 OABC 的面积，则根据平均速度的定义，该 匀速直线运动的速度就等于匀加速直线运动的平均速度。当矩形 ODEC 的面积与梯形 OABC 的面积相等时，容易得出， ADF△ 与 BEF△ 全等，因此 F 为 AB 的中点，有 0 2 tv vv  。又因为 F 点所对 应的时刻为 2 t ，因此还可得 2 tv v 。证毕。 有了匀变速直线运动的平均速度公式，结合图像下方的面积表示运动的距离，我们可以解决很 多匀变速运动的问题。 例 3 如图 3.27 为某物体由静止做直线运动的 v t 图像，则下列说法 正确的是( )。 A． 1 2 3: : 1: 2:3v v v  B．每经过相同的时间，物体的速度增加量都相同 C．物体在 00 ~ t ， 00 ~ 2t ， 00 ~ 3t 时间内运动的距离之比为 1:2:3 D．物体在 00 ~ t ， 0 0~ 2t t ， 0 02 ~ 3t t 时间内平均速度之比为 1:3:5 分析与解 由题给 v t 图像可知，物体的速度与时间成正比，均匀增加，因此每经过相同的时 间，物体的速度增加量都相同，结合正比例知识，可知 1 2 3: : 1: 2:3v v v  ，因此 A，B 选项正确。 由于 v t 图像下方的面积表示运动距离，因此物体在 00 ~ t ， 00 ~ 2t ， 0 02 ~ 3t t 时间内运动的距离 分别为对应的三角形面积，又由三角形面积之比等于边长的平方之比，可得运动距离之比为    2 22 0 0 0: 2 : 3 1: 4:9t t t  ，C 选项错误。结合匀变速直线运动的平均速度公式，物体 00 ~ t ，0 0~ 2t t ， 0 02 ~ 3t t 时间内平均速度之比为 2 31 1 20 : :2 2 2 v vv v v   ，又因为 1 2 3: : 1: 2:3v v v  ，因此可得 2 31 1 20 : : 1:3:52 2 2 v vv v v    ，D 选项正确。本题正确选项为 ABD。 练习题 1．下列图像表示匀减速直线运动的是( )。 A B C D 2．小球在斜面上从静止开始匀加速下滑，进人水平面后又做匀减速直线运动直至停止。下列图 像中可以反映小球这一运动过程中速度大小变化的是( )。 A B C D 3．一物体从静止开始做匀加速直线运动，时间t 内通过的距离为 s ，则它从出发开始，在 3 s 时 间内的位移 s 和从开始出发经路程所需时间t 分别为( )。 A． 1 3s s  ， 1 3t t  B． 1 9s s  ， 3 3t t  C． 1 6s s  ， 1 6t t  D． 1 9s s  ， 1 9t t  4．从某一高度相隔1s 先后释放两个相同的小球甲和乙，不计空气阻力，图 3.28 所示为两球释 放后的速度-时间图像，在空中任一时刻( )。 A．甲、乙两球距离始终保持不变，甲、乙两球速度之差保持不变 B．甲、乙两球距离越来越大，甲、乙两球速度之差也越来越大 C．甲、乙两球距离越来越大，但甲、乙两球速度之差不变 D．甲、乙两球距离越来越小，甲、乙两球速度之差也越来越小 5．如图3.29所示为 A ， B 两物体同时由同一地点向同一方向做直线运 动的 v t 图像，由图像可知( )。 A． B 做匀速运动， A 静止 B． 20s 末 A ， B 相遇 C． 40s 末 A ， B 相遇 D． A 做匀速运动， B 做匀加速运动 6．物体做匀加速直线运动，已知第1s 末的速度是 6m / s ，第 2s 末的速度是8m / s ，则下面结 论正确的是( )。 A．物体的初速度是3m / s B．物体第 4s 末的速度是12m / s C．任何1s 内的速度变化都是 2m / s D．第1s 内的平均速度是5m / s 7．做匀加速直线运动的物体，速度由 v 增加到 2v 时的位移为 s ，则当速度由3v 增加到 4v 时的 位移是( )。 A． 5 2 s B． 7 3 s C．3s D． 4s 8．做匀加速直线运动的物体，在某一段时间t 内经过的位移是 s ，则 /s t 表示( )。 A．物体在t 时间内速度的增加量 B．物体在t 时间内的位移中点的瞬时速度 C．物体在t 时间内中间时刻的瞬时速度 D．物体在t 时间内的平均速度 9．一个以初速度 0v 沿直线运动的物体， st 末速度为 tv ，如图 3.30 所示，则关于 st 内物体运动 的平均速度v 和加速度 a 的说法中正确的是( )。 A． 0 2 tv vv  B． 0 2 tv vv  C．物体速度的增加是均匀的 D．物体速度的增加越来越慢 10．某物体做直线运动，若前一半路程速度为 1v ，后一半路程速度为 2v ， 则全程的平均速度为________；若前一半时间速度为 1v ，后一半时间速度为 2v ，则全程的平均速度 为________。 11．一辆汽车沿着平直公路以速度 1v 行驶 2/3 路程，接着以 2 20km / hv  跑完余下的 1/3 路程， 如果汽车全程的平均速度为 28km / hv  ，则汽车在前 2/3 路程的速度 1v  ________。 12．一个物体从静止开始做匀加速直线运动，那么它在3s 末和 6s 末的速度之比为________，它 在前3s 内和前 6s 内运动的距离之比为________。 13．一物体由静止做匀加速直线运动，试计算下列各小题： (1)速度为 4m / s 时，运动距离为8m ；速度为8m / s 时，运动距离为________。 (2)速度为 2m / s 时，走了5m ；要使速度达到 6m / s ，还要走________。 (3)前5s 内走了10m ，则前10s 内走了________。 (4)前 4s 内走了10m ，则再走 4s 还能走________。 (5)走前 2m 需 4s，走前 4m需________。 (6)走前 3m 需5s ，再走 3m 还要________。 (7)第1个5s 走8m ，第10个5s 走________。 (8)通过10m 的距离时，速度达到 2m / s ，再通过10m 距离时速度达到________。 (9)前 2s 内通过的距离和后3s (共走5s )内通过的距离之比为________。 (10)共走5m ，通过前 2m 所需时间和通过后 3m 所需时间之比为________。 14．如图 3.31 所示是某物体做直线运动的 v t 图像，则物 体在 0 ~ 2s 内做________运动，通过的距离是________ m ；物 体在 2 ~ 4s 做________运动，通过的距离是________ m ；物体 在 4 ~ 5s 做________运动，通过的距离是________ m ；物体在 m 内的平均速度为________ m 。 参考答案 1．A。匀减速直线运动的速度—时间图像是一条直线，速度均匀减小。B 选项为匀速直线运动， C 选项表示物体做匀速直线运动，D 选项表示物体静止。 2．C。小球的速度-时间图像应是两段直线：沿斜面滑下时速度均匀增加，进人水平面后速度均 匀减小，直至减为零。 3．B。速度—时间图像下方的面积表示物体通过的距离，面积与底边长度(即时间)的平方成正 比，则有 2 2 2 1 3 3 ss s t tt       ，解得 1 9s s  ， 3 3t t  。 4．C。由图像可知，在 1st  时，乙刚开始下落，而甲的速度已经达到9.8m / s 。甲和乙的速度 —时间图像为平行直线，说明甲、乙在相同时间内速度的增加量相同，因此，在以后的运动过程中， 甲的速度总是比乙大9.8m / s ，甲在乙的前方，甲、乙之间的距离也越来越大。 5．CD。由图像可知， A 做匀速直线运动，B 做匀加速直线运动。两物体同时同地同方向运动， 则相遇时，通过的距离一定相等，根据速度-时间图像下方的面积表示物体前进的距离，可知在 40s 末， A ， B 两物体相遇。 6．BD。物体在第1s 末到第 2s末速度由 6m / s 增加到8m / s ，说明物体每经过1s ，速度将增加 2m / s ，因此在 0t  时，物体的速度(初速度)应为 4m / s 。第 4s 末物体的速度应为12m / s ，第1s 内 的平均速度为 4 6 m / s 5m / s2v   。 7．B。物体做匀加速直线运动，则物体速度从v 增加到 2v 和从3v 增加到 4v 所用时间相同，设 这个时间为 t ，则由匀加速直线运动的平均速度公式，可得速度从 v 增加到 2v 通过的距离为 2 2 v vs t ，速度从3v 增加到 4v 通过的距离 3 4 2 v vs t  ，显然 7 s3s  。 8．CD。由本节例 2 的结论，匀变速直线运动的平均速度等于初末速度的和的一半，也等于中 间时刻的瞬时速度，写成公式可以表示为 1 2 1 22 v vsv vt    ；因此 CD 正确。 9．BD。物体的速度一时间图像是曲线，在 0 ~ t 时间内物体的速度从 0v 增加到 tv ，通过的距离 是曲线下方的面积，显然这个面积大于物体做匀加速直线运动时速度从 0v 增加到 tv 的图线下方的面 积，即物体的平均速度 0 2 tv vv  。 10． 1 2 1 2 2v v v v ， 1 2 2 v v 。设路程为 2s ，则一半路程为 s ，物体在前半程和后半程所用的时间分 别为 1 1 st v  和 2 2 st v  ，则全程的平均速度为 1 2 1 2 1 2 1 2 22 2 v vs sv s st t v v v v     。设总时间为 2t ，则一 半的时间为t ，物体在前一半时间和后一半时间通过的路程分别为 1 1s v t 和 2 2s v t ，则全程的平均 速度为 1 2 1 2 2 2 v t v t v vv t    。 11．35km / h 。设汽车通过的总路程为 s ，则汽车通过前 2 3 s 的路程用时 1 1 2 3 s t v  ，汽车通过后 1 3 s 的路程用时 2 2 1 3 s t v  ，故全程的平均速度为 1 2 1 2 2 1 3 3 s sv t t S S v v    ，解得 1 35km / hv  。 12．1：2，1：4。初速度为零的匀加速直线运动的速度—时间图像为过坐标原点的倾斜直线， 速度之比等于时间之比，运动距离之比等于图像下方面积之比，即等于时间的平方之比。 13．(1)32m ；(2) 40m ；(3) 40m ；(4)30m ；(5) 4 2s ；(6)  5 2 1 s ；(7)152m ；(8) 2 2m / s ； (9)4：21；(10)  2 : 5 2 。 本题的各小题均可利用“初速度为零的匀加速直线运动的速度—时间图像为过坐标原点的倾斜 直线，速度之比等于时间之比，运动距离之比等于图像下方面积之比，即等于时间的平方之比”这 一规律求解。 14．匀加速直线，2；匀速直线，4；匀减速直线，1；1.4。物体在 0 ~ 2s 内的速度—时间图像 为过坐标原点的倾斜直线，因此物体做匀加速直线运动；通过的距离为 0 ~ 2s 内图像下方的面积， 即 1 1 2m / s 2s 2m2s     。物体在 2 ~ 4s 的速度-时间图像为平行于时间轴的直线，因此物体做匀 速直线运动，物体在 2 ~ 4s 内运动的距离  2 2m / s 4s 2ss     4m 。物体在 4 ~ 5s 的速度—时 间图像为向下倾斜的直线，因此物体做匀减速直线运动，至 1 5st  时速度减为零，物体在 4 ~ 5s 内 运 动 的 距 离  3 1 2m / s 5s 4s 1m2s      。 在 0 ~ 5s 内 物 体 的 平 均 速 度 为 1 2 3s s sv t    总 2m 4m 1m 1.4m / s5s    。