中考数学全程复习方略第二十讲矩形菱形正方形课件 62页

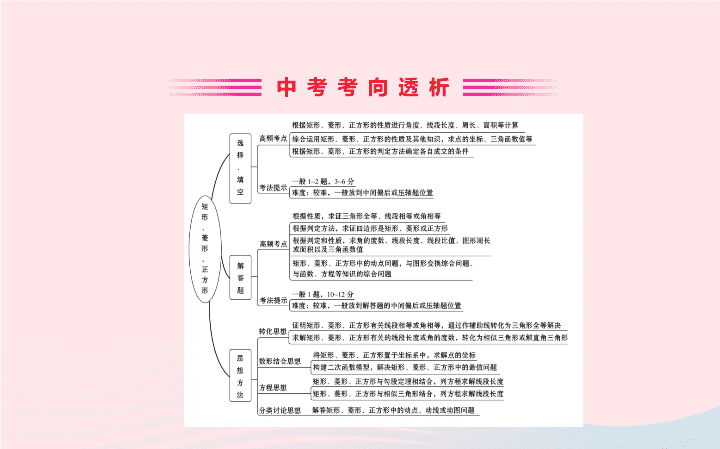
第二十讲 　 矩形、菱形、正方形 考点一　矩形的性质与判定 【 主干必备 】 性质 除具有平行四边形的性质外 , 还有 : 1. 矩形的四个角都是 __________ 2. 矩形的对角线 __________ 3. 既是 _____________ 图形 , 又是轴对称图形  判定 1. 有一个角是 _________ 的平行四边形  2. 对角线 _________ 的平行四边形  3. 有三个角是 _________ 的四边形  　直角　  　相等　  　中心对称　 　直角　 　相等　 　直角　 【 微点警示 】 (1) 矩形的分割 : 矩形被对角线所 分成的四个三角形都是等腰三角 形 , 它们相对的两个全等 , 它们的 面积都相等 . (2) 判定的思路 : 若起点是四边形 , 需加上三个角是直角才得到矩形 ; 若起点是平行四边形 , 加上一个角是直角或对角线相等便得到矩形 . 【 核心突破 】 例 1(2019· 青岛中考 ) 如图 , 在 ▱ ABCD 中 , 对角线 AC 与 BD 相交于点 O, 点 E,F 分别为 OB,OD 的中点 , 延长 AE 至 G, 使 EG=AE, 连接 CG. (1) 求证 :△ABE≌△CDF. (2) 当 AB 与 AC 满足什么数量关系时 , 四边形 EGCF 是矩形 ? 请说明理由 . 【 思路点拨 】 (1) 由平行四边形的性质得出 AB=CD, AB∥CD,OB=OD,OA=OC, 由平行线的性质得出∠ ABE= ∠CDF, 证出 BE=DF, 由 SAS 证明△ ABE≌△CDF 即可 . (2) 证出 AB=OA, 由等腰三角形的性质得出 AG⊥OB, ∠OEG=90°, 同理 :CF⊥OD, 得出 EG∥CF, 由三角形中位线定理得出 OE∥CG, 所以 EF∥CG, 得出四边形 EGCF 是平行四边形 , 即可得出结论 . 【 自主解答 】 略 【 明 · 技法 】 矩形判定方法的选择技巧 (1) 若易证得四边形是平行四边形 , 则再证一角为直角或对角线相等 , 即可证得其是矩形 . (2) 三个角是直角的四边形是矩形 . (3) 有两条对角线相等的四边形不一定是矩形 , 必须加上“平行四边形”这个条件 , 它才是矩形 . (4) 对角线相等且互相平分的四边形是矩形 . 【 题组过关 】 1.(2019· 临沂中考 ) 如图 , 在平行四边形 ABCD 中 ,M,N 是 BD 上两点 ,BM=DN, 连接 AM,MC,CN,NA, 添加一个条件 , 使 四边形 AMCN 是矩形 , 这个条件是 ( 　 　 ) A A.OM= AC 　　　　　　 B.MB=MO C.BD⊥AC D.∠AMB=∠CND 2. 如图 , 延长矩形 ABCD 的边 BC 至点 E, 使 CE=CA, 连接 AE, 如果∠ ACB=40°, 则∠ E 的值是 ( 　 　 ) A.18° 　　　 B.19° 　　　 C.20° 　　　 D.40° C 3.(2019· 昆明西山区模拟 ) 如图 , 在矩形 ABCD 中 , 对角 线 AC,BD 相交于点 O,∠AOB=60°,AC=4 cm, 则矩形 ABCD 的面积为 世纪金榜导学号 ( 　 　 ) B A.12 cm 2 B.4 cm 2 C.8 cm 2 D.6 cm 2 4.(2019· 甘肃中考 ) 如图 , 在矩形 ABCD 中 ,AB=10, AD=6,E 为 BC 上一点 , 把△ CDE 沿 DE 折叠 , 使点 C 落在 AB 边 上的 F 处 , 则 CE 的长为 ______.  5.(2019· 怀化中考 ) 已知 : 如图 , 在 ▱ ABCD 中 ,AE⊥BC, CF⊥AD,E,F 分别为垂足 . 世纪金榜导学号 (1) 求证 :△ABE≌△CDF. (2) 求证 : 四边形 AECF 是矩形 . 【 证明 】 (1)∵ 四边形 ABCD 是平行四边形 ,∴∠B=∠D,AB=CD,AD∥BC, ∵AE⊥BC,CF⊥AD,∴∠AEB=∠AEC=∠CFD=∠AFC=90°, 在△ ABE 和△ CDF 中 , ∴△ABE≌△CDF(AAS). (2)∵AD∥BC,∴∠EAF=∠AEB=90°,∴∠EAF=∠AEC= ∠AFC=90°,∴ 四边形 AECF 是矩形 . 考点二　菱形的性质与判定 【 主干必备 】 性质 除具有平行四边形的性质外 , 还有 : 1. 菱形的四条边都 __________ 2. 菱形的两条对角线互相 _________, 并且每一条 对角线平分 ______________ 3. 菱形的面积等于两条对角线乘积的 __________ 4. 既是 _____________ 图形 , 又是轴对称图形  　相等　  　垂直　 　一组对角　  　一半　  　中心对称　 判定 1. 有一组邻边 _________ 的平行四边形  2. 对角线互相 _________ 的平行四边形  3. 四条边都 _________ 的四边形  　相等　 　垂直　 　相等　 【 微点警示 】 (1) 菱形的分割 : 菱形被对角线所分成的四个三角形都是直角三角形 , 它们四个都全等 . (2) 判定的思路 : 若起点是四边形 , 需加上四条边都相等才得到菱形 ; 若起点是平行四边形 , 加上一组邻边相等或对角线互相垂直便得到菱形 . 【 核心突破 】 例 2(2019· 兰州中考 ) 如图 ,AC=8, 分别以 A,C 为圆心 , 以长度 5 为半径作弧 , 两条弧分别相交于点 B 和 D. 依次连接 A,B,C,D, 连接 BD 交 AC 于点 O. (1) 判断四边形 ABCD 的形状并说明理由 . (2) 求 BD 的长 . 【 思路点拨 】 (1) 利用作法得到四边相等 , 从而可判断四边形 ABCD 的形状 . (2) 根据菱形的性质得 OA=OC=4,OB=OD,AC⊥BD, 然后利用勾股定理计算出 OB, 从而得到 BD 的长 . 【 自主解答 】 略 【 明 · 技法 】 菱形判定方法的选择 (1) 若四边形 ( 或可证 ) 为平行四边形 , 则再证一组邻边相等或对角线互相垂直 . (2) 若相等的边较多 ( 或容易证出 ) 时 , 可证四条边相等 . 【 题组过关 】 1.(2019· 天津中考 ) 如图 , 四边形 ABCD 为菱形 ,A,B 两点 的坐标分别是 (2,0),(0,1), 点 C,D 在坐标轴上 , 则菱形 ABCD 的周长等于 ( 　 　 ) C A. 　　　　 B.4 　　　 C.4 　　　 D.20 2. 如图 , 四边形 ABCD 为平行四边形 , 延长 AD 到 E, 使 DE=AD, 连接 EB,EC,DB, 添加一个条件能使四边形 DBCE 成为菱形 的是 ( 　 　 ) B A.AB=BE B.AB⊥BE C.∠ADB=90° D.CE⊥DE 3.(2019· 北部湾中考 ) 如图 , 在菱形 ABCD 中 , 对角线 AC,BD 交于点 O, 过点 A 作 AH⊥BC 于点 H, 已知 BO=4, S 菱形 ABCD =24, 则 AH=______. 世纪金榜导学号  4.( 生活情境题 ) 如图 , 把两张宽度都是 3 cm 的纸条交错 地叠在一起 , 相交成角 α. 则重叠部分的面积为 __________. 世纪金榜导学号  5.(2019· 枣庄中考 ) 如图 ,BD 是菱形 ABCD 的对角线 ,∠CBD=75°, (1) 请用尺规作图法 , 作 AB 的垂直平分线 EF, 垂足为 E, 交 AD 于 F.( 不要求写作法 , 保留作图痕迹 ) (2) 在 (1) 的条件下 , 连接 BF, 求∠ DBF 的度数 . 【 解析 】 (1) 略 (2)∵ 四边形 ABCD 是菱形 ,∴∠ABD=∠DBC= ∠ABC=75°,DC∥AB,∠A=∠C. ∴∠ABC=150°,∠ABC+∠C=180°,∴∠C=∠A=30°, ∵EF 垂直平分线段 AB,∴AF=FB,∴∠A=∠FBA=30°, ∴∠DBF=∠ABD-∠FBE=45°. 考点三　正方形的性质与判定 【 主干必备 】 性质 1. 正方形的四条边都 _________.  2. 正方形的四个角都是 _________.  3. 正方形的两条对角线 _________ 且互相 _____________, 每一条对角线平分一组对角 .  4. 既是 _________________, 又是轴对称图形 .  　相等　 　直角　 　相等　 　垂直平分　 　中心对称图形　 判定 1. 有一组邻边 _________ 并且有一个角是 _________ 的平行四边形  2. 有一组邻边 _________ 的矩形  3. 有一个角是 _________ 的菱形  4. 对角线相等且垂直的平行四边形 　相等　 　直角　 　相等　 　直角　 【 微点警示 】 (1) 正方形的分割 : 正方形被对角线所分成的四个三角形都是等腰直角三角形 , 它们四个都全等 . (2) 判定的思路 : 若起点是平行四边形 , 需加上邻边相等和一个直角 , 或者加上对角线相等且垂直才得到正方形 ; 若起点是矩形 , 加上一组邻边相等便得到正方形 ; 若起点是菱形 , 加上一个直角便得到正方形 . 【 核心突破 】 例 3 【 原型题 】 (2018· 聊城中考 ) 如图 , 正方形 ABCD 中 ,E 是 BC 上的一点 , 连接 AE, 过点 B 作 BH⊥AE, 垂足为点 H, 延长 BH 交 CD 于点 F, 连接 AF. (1) 求证 :AE=BF. (2) 若正方形边长是 5,BE=2, 求 AF 的长 . 【 思路点拨 】 (1) 利用正方形的性质证明△ ABE≌△BCF, 进而得到对应边 AE=BF. (2) 借助△ ABE≌△BCF, 求出 DF 的值 , 然后在 Rt△ADF 中使用勾股定理求得 AF 的值 . 【 自主解答 】 (1)∵ 四边形 ABCD 是正方形 ,∴AB=BC,∠ABC=∠C=90°, ∵ 作 BH⊥AE, 垂足为点 H,∴∠BAE=∠CBF. 在△ ABE 和△ BCF 中 , ∴△ABE≌△BCF(ASA),∴AE=BF. (2) 略 【 变形题 1】 ( 变换结论 ) 如图 , 正方形 ABCD 中 ,E 是 BC 上的一点 , 连接 AE, 过 B 点作 BH⊥AE, 垂足为点 H, 延长 BH 交 CD 于点 F, 连接 AF. 若正方形边长是 5,BE=2, 求 FH 的长 . 【 解析 】 在 Rt△ABE 中 ,∵AB=5,BE=2, ∴AE= ∵S △ABE = ∴BH= ∵BF=AE= ∴FH=BF-BH= 【 变形题 2】 ( 变换条件、结论 ) 如图 , 正方形 ABCD 中 ,E 是 BC 上的一点 , 连接 AE, 过 B 点作 BH⊥AE, 垂足为点 H, 延长 BH 交 CD 于点 F, 连接 BD, 交 AE 于点 N, 连接 AC, 分别交 BD,BF 于点 O,M, 连接 HO, 求证 :HO 平分∠ AHF. 略 【 明 · 技法 】 正方形判定及性质的应用技巧 (1) 判定的两种思路 : 证明一个四边形是正方形 , 可以先判定为矩形 , 再证邻边相等或对角线互相垂直 ; 或先判定为菱形 , 再证一个角是直角或对角线相等 . (2) 性质的兼容并蓄 : 正方形既是特殊的矩形又是特殊的菱形 , 具有它们所有的性质 . (3) 易得全等三角形 : 正方形被两条对角线分割为四个全等的等腰直角三角形 , 在正方形中对称画出分割线 , 很容易得到另外的全等三角形 . 【 题组过关 】 1. (2019· 枣庄中考 ) 如图 , 点 E 是正方形 ABCD 的边 DC 上 一点 , 把△ ADE 绕点 A 顺时针旋转 90° 到△ ABF 的位置 . 若 四边形 AECF 的面积为 20,DE=2, 则 AE 的长为 ( 　 　 ) D A.4 　　　 B.2 　　　 C.6 　　　 D.2 2.( 易错警示题 ) 满足下列条件的四边形是正方形的是 ( 　 　 ) A. 对角线互相垂直平分的平行四边形 B. 对角线互相平分且相等的矩形 C. 对角线互相垂直平分的菱形 D. 对角线互相垂直平分且相等的四边形 D 3. 如图 , 在边长为 3 的正方形 ABCD 中 , 点 E 是 BC 边上的 点 ,EC=2,∠AEP=90°, 且 EP 交正方形外角的平分线 CP 于 点 P, 则 PC 的长为 ______ .  4.(2019· 滁州模拟 ) 如图 , 在正方形 ABCD 中 ,AC,BD 相交 于点 O,E,F 分别为 BC,CD 上的两点 ,BE=CF,AE,BF 分别交 BD,AC 于 M,N 两点 , 连接 OE,OF. 下列结论 :①AE=BF; ②AE⊥BF;③CE+CF= BD; ④S 四边形 OECF = S 正方形 ABCD , 其中正确的序号是 _____________. 世纪金榜导学号  　①②③④　 5.(2019· 河北模拟 ) 如图 , 点 E 是正方形 ABCD 对角线 AC 上一点 ,EF⊥AB,EG⊥BC, 垂足分别为 F,G, 若正方形 ABCD 的周长是 40 cm. 世纪金榜导学号 (1) 求证 : 四边形 BFEG 是矩形 . (2) 求四边形 EFBG 的周长 . (3) 当 AF 的长为多少时 , 四边形 BFEG 是正方形 ? 略