2008年数学中考试题分类汇编（函数与几何图形1） 31页

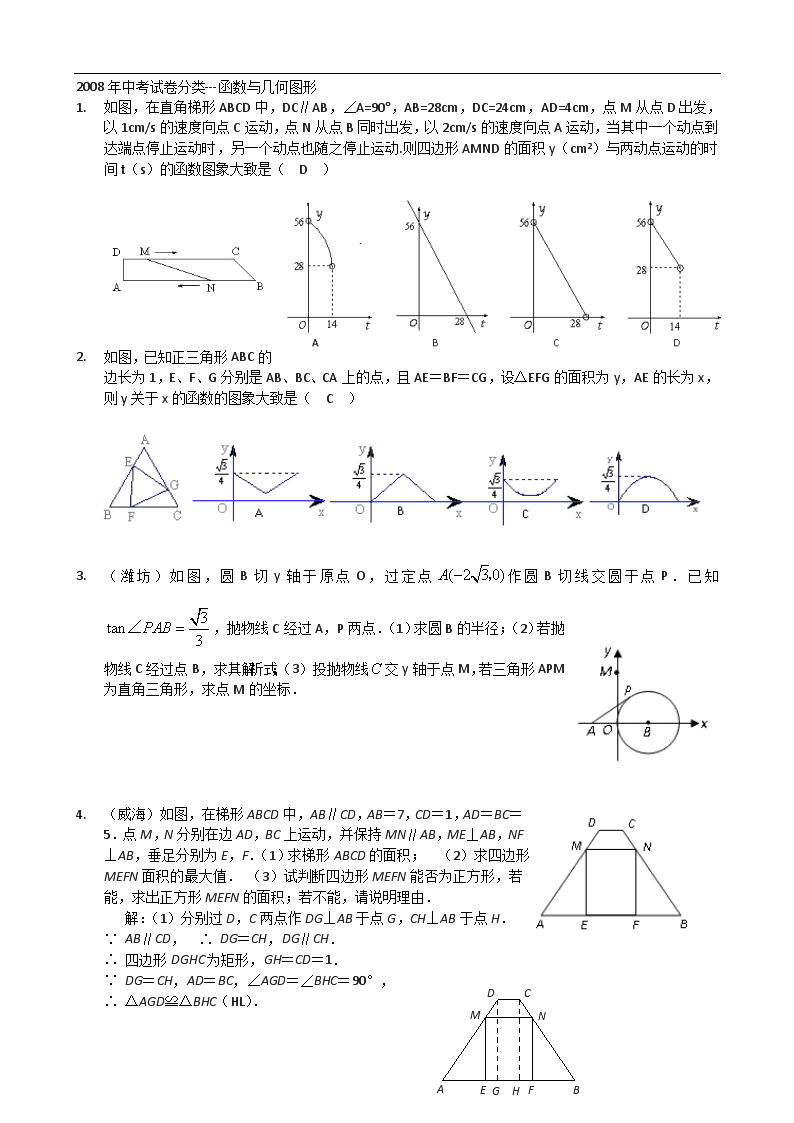
‎2008年中考试卷分类---函数与几何图形 1. 如图，在直角梯形ABCD中，DC∥AB，∠A=90°，AB=28cm，DC=24cm，AD=4cm，点M从点D出发，以1cm/s的速度向点C运动，点N从点B同时出发，以2cm/s的速度向点A运动，当其中一个动点到达端点停止运动时，另一个动点也随之停止运动.则四边形AMND的面积y（cm2）与两动点运动的时间t（s）的函数图象大致是（ D ）‎ 2. 如图，已知正三角形ABC的边长为1，E、F、G分别是AB、BC、CA上的点，且AE＝BF＝CG，设△EFG的面积为y，AE的长为x，则y关于x的函数的图象大致是（ C ）‎ 3. ‎（潍坊）如图，圆B切y轴于原点O，过定点作圆B切线交圆于点P．已知，抛物线C经过A，P两点．（1）求圆B的半径；（2）若抛物线C经过点B，求其解析式；（3）投抛物线交y轴于点M，若三角形APM为直角三角形，求点M的坐标．‎ ‎ ‎ 4. ‎（威海）如图，在梯形ABCD中，AB∥CD，AB＝7，CD＝1，AD＝BC＝5．点M，N分别在边AD，BC上运动，并保持MN∥AB，ME⊥AB，NF⊥AB，垂足分别为E，F．（1）求梯形ABCD的面积； （2）求四边形MEFN面积的最大值． （3）试判断四边形MEFN能否为正方形，若能，求出正方形MEFN的面积；若不能，请说明理由．‎ ‎ 解：（1）分别过D，C两点作DG⊥AB于点G，CH⊥AB于点H． ‎ ‎∵ AB∥CD， ∴ DG＝CH，DG∥CH． ‎ ‎∴ 四边形DGHC为矩形，GH＝CD＝1． ‎ C D A B E F N M G H ‎∵ DG＝CH，AD＝BC，∠AGD＝∠BHC＝90°，‎ ‎∴ △AGD≌△BHC（HL）． ‎ ‎∴ AG＝BH＝＝3． ………2分 ‎ ‎∵ 在Rt△AGD中，AG＝3，AD＝5， ‎ ‎∴ DG＝4． ∴ ． ‎ C D A B E F N M G H ‎（2）∵ MN∥AB，ME⊥AB，NF⊥AB， ‎ ‎∴ ME＝NF，ME∥NF． ∴ 四边形MEFN为矩形． ‎ ‎∵ AB∥CD，AD＝BC， ∴ ∠A＝∠B． ‎ ‎∵ ME＝NF，∠MEA＝∠NFB＝90°， ‎ ‎∴ △MEA≌△NFB（AAS）．∴ AE＝BF． ‎ 设AE＝x，则EF＝7－2x． ‎ ‎∵ ∠A＝∠A，∠MEA＝∠DGA＝90°， ‎ ‎∴ △MEA∽△DGA．∴ ．∴ ME＝． ‎ ‎∴ ． ‎ 当x＝时，ME＝＜4，∴四边形MEFN面积的最大值为． ‎ ‎（3）能． 由（2）可知，设AE＝x，则EF＝7－2x，ME＝． ‎ 若四边形MEFN为正方形，则ME＝EF． 即 7－2x．解，得 ． ‎ ‎∴ EF＝＜4． ‎ ‎∴ 四边形MEFN能为正方形，其面积为．‎ 1. ‎（青岛）已知：如图①，在RtΔABC中，∠C=900，AC=4cm，BC=3cm，点P由B出发沿BA方向向点A匀速运动，速度为1cm/s；点Q由A出发沿AC方向向点C匀速运动，速度为2cm/s；连接PQ．若设运动的时间为t（s）（01的常数），设过Q、R两点，且以QR的垂直平分线为对称轴的抛物线与y轴的交点为N，其顶点为M，记△QNM的面积为S△QNM，△QNR的面积S△QNR，求S△QNM：S△QNR的值. ‎ 2. ‎（重庆）已知：如图，抛物线y=ax2-2ax+c（a≠0）与y轴交于点C（0，4），与x轴交于点A、B，点A的坐标为（4，0）。（1）求该抛物线的解析式；（2）点Q是线段AB上的动点，过点Q作QE∥AC，交BC于点E，连接CQ。当ΔCQE的面积最大时，求点Q的坐标；（3）若平行于x轴的动直线与该抛物线交于点P，与直线AC交于点F，点D的坐标为（2，0）。问：是否存在这样的直线，使得△ODF是等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由。‎ 3. ‎（东营）在△ABC中，∠A＝90°，AB＝4，AC＝3，M是AB上的动点（不与A，B重合），过M点作MN∥BC交AC于点N．以MN为直径作⊙O，并在⊙O内作内接矩形AMPN．令AM＝x．（1）用含x的代数式表示△ＭNP的面积S；（2）当x为何值时，⊙O与直线BC相切？（3）在动点M的运动过程中，记△ＭNP与梯形BCNM重合的面积为y，试求y关于x的函数表达式，并求x为何值时，y的值最大，最大值是多少？‎ 解：（1）∵MN∥BC，∴∠AMN=∠B，∠ANM＝∠C． ‎ A B C M N P 图 1‎ O ‎ ∴ △AMN ∽ △ABC．‎ ‎∴ ，即．‎ ‎∴ AN＝x． ‎ ‎∴ =．（0＜＜4） ‎ A B C M N D 图 2‎ O Q ‎（2）如图2，设直线BC与⊙O相切于点D，连结AO，OD，则AO =OD =MN．‎ 在Rt△ABC中，BC ＝=5．‎ ‎ 由（1）知 △AMN ∽ △ABC． ‎ ‎∴ ，即． ‎ ‎∴ ，∴ ． ‎ 过M点作MQ⊥BC 于Q，则． 在Rt△BMQ与Rt△BCA中，∠B是公共角，‎ ‎∴ △BMQ∽△BCA．∴ ．∴ ，． ‎ ‎∴ x＝． ∴ 当x＝时，⊙O与直线BC相切． ‎ A B C M N P 图 3‎ O ‎（3）随点M的运动，当P点落在直线BC上时，连结AP，则O点为AP的中点．‎ ‎∵ MN∥BC，∴ ∠AMN=∠B，∠AOM＝∠APC．‎ ‎∴ △AMO ∽ △ABP． ‎ ‎∴ ． AM＝MB＝2． ‎ 故以下分两种情况讨论： ‎ ‎① 当0＜≤2时，． ‎ ‎∴ 当＝2时， ‎ ‎② 当2＜＜4时，设PM，PN分别交BC于E，F．‎ A B C M N P 图 4‎ O E F ‎∵ 四边形AMPN是矩形， ‎ ‎∴ PN∥AM，PN＝AM＝x． ‎ 又∵ MN∥BC， ‎ ‎∴ 四边形MBFN是平行四边形． ‎ ‎∴ FN＝BM＝4－x． ‎ ‎∴ ． ‎ 又△PEF ∽ △ACB． ‎ ‎∴ ．∴＝．‎ 当2＜＜4时，． ‎ ‎∴ 当时，满足2＜＜4，． ‎ 综上所述，当时，值最大，最大值是2．‎ 1. ‎（上海）正方形ABCD的边长为2，E是射线CD上的动点（不与点D重合），直线AE交直线BC于点G，∠BAE的平分线交射线BC于点O．（1）如图8，当CE=时，求线段BG的长；（2）当点O在线段BC上时，设，BO=y，求y关于x的函数解析式；（3）当CE=2ED时，求线段BO的长．‎ ‎ 解：（1）在边长为2的正方形中，，得，‎ 又∵，即，∴，得． ‎ ‎∵，∴； ‎ ‎（2）当点在线段上时，过点作，垂足为点，‎ ‎∵为的角平分线，，∴． ‎ 在正方形中，，∴．‎ ‎∵，∴． ‎ 又∵，，得．‎ ‎∵在Rt△ABG中，，，，‎ ‎∴．‎ ‎∵，∴．‎ ‎∵，即，得，；‎ ‎（3）当时，‎ ‎①当点在线段上时，即，由（2）得； ‎ ‎②当点在线段延长线上时，‎ ‎，，在 Rt△ADE中，．‎ 设交线段于点，∵是的平分线，即，‎ 又∵，∴．∴．‎ ‎∴．∴． ‎ ‎∵，∴，即，得．‎ 2. ‎（中山）如图11，在梯形ABCD中，AD∥BC，AB=AD=DC=2cm，BC=4cm，在等腰△PQR中，∠QPR=120°，底边QR=6cm，点B、C、Q、R在同一直线l上，且C、Q两点重合，如果等腰△PQR以1cm/秒的速度沿直线 l箭头所示方向匀速运动，t秒时梯形ABCD与等腰△PQR重合部分的面积记为S平方厘米。（1）当t=4时，求S的值；（2）当4≤t≤10，求S与t的函数关系式，并求出S的最大值。‎ ‎ （1）t＝4时,Q与B重合，P与D重合，‎ 重合部分是＝‎ 1. 如图：抛物线经过A（－3，0）、B（0，4）、C（4，0）三点． （1） 求抛物线的解析式． （2）已知AD ＝ AB（D在线段AC上），有一动点P从点A沿线段AC以每秒1个单位长度的速度移动；同时另一个动点Q以某一速度从点B沿线段BC移动，经过t 秒的移动，线段PQ被BD垂直平分，求t的值； （3）在（2）的情况下，抛物线的对称轴上是否存在一点M，使MQ＋MC的值最小？若存在，请求出点M的坐标；若不存在，请说明理由．‎ ‎ （1）解法一：设抛物线的解析式为y ＝ a (x ＋3 )(x － 4)‎ ‎ 因为B（0，4）在抛物线上，所以4 ＝ a ( 0 ＋ 3 ) ( 0 － 4 )解得a＝ －1/3‎ ‎ 所以抛物线解析式为 解法二：设抛物线的解析式为，‎ 依题意得：c＝4且 解得 ‎ 所以 所求的抛物线的解析式为 ‎（2）连接DQ，在Rt△AOB中，‎ 所以AD＝AB＝ 5，AC＝AD＋CD＝3 ＋ 4 ＝ 7，CD ＝ AC － AD ＝ 7 – 5 ＝ 2‎ 因为BD垂直平分PQ，所以PD＝QD，PQ⊥BD，所以∠PDB＝∠QDB 因为AD＝AB，所以∠ABD＝∠ADB，∠ABD＝∠QDB，所以DQ∥AB 所以∠CQD＝∠CBA．∠CDQ＝∠CAB，所以△CDQ∽ △CAB ‎ 即 所以AP＝AD – DP ＝ AD – DQ＝5 –＝ ，‎ 所以t的值是 ‎（3）答对称轴上存在一点M，使MQ＋MC的值最小 理由：因为抛物线的对称轴为 所以A（－ 3，0），C（4，0）两点关于直线对称 连接AQ交直线于点M，则MQ＋MC的值最小 过点Q作QE⊥x轴，于E，所以∠QED＝∠BOA＝900‎ ‎ DQ∥AB，∠ BAO＝∠QDE， △DQE ∽△ABO ‎ 即 ‎ 所以QE＝，DE＝，所以OE ＝ OD ＋ DE＝2＋＝，所以Q（，）‎ 设直线AQ的解析式为 则 由此得 ‎ 所以直线AQ的解析式为 联立 由此得 所以M 则：在对称轴上存在点M，使MQ＋MC的值最小．‎ 1. ‎（龙岩）如图，等腰梯形ABCD中，AB=4，CD=9，∠C=60°，动点P从点C出发沿CD方向向点D运动，动点Q同时以相同速度从点D出发沿DA方向向终点A运动，其中一个动点到达端点时，另一个动点也随之停止运动.（1）求AD的长；（2）设CP=x，问当x为何值时△PDQ的面积达到最大，并求出最大值；（3）探究：在BC边上是否存在点M使得四边形PDQM是菱形？若存在，请找出点M，并求出BM的长；不存在，请说明理由.‎ ‎ （1）解法一：如图25-1‎ 过A作AE⊥CD，垂足为E .‎ ‎ 依题意，DE=. …………………………2分 ‎ 在Rt△ADE中，AD=. ………5分 图25-1‎ ‎ 解法二：如图25-2‎ ‎ 过点A作AE∥BC交CD于点E，则CE=AB=4 . …2分 ‎ ∠AED=∠C=60°.‎ ‎ 又∵∠D=∠C=60°，‎ ‎ ∴△AED是等边三角形 . ‎ ‎ ∴AD=DE=9－4=5 . …………………………………5分 ‎ （2）解：如图25-1‎ 图25-2‎ ‎∵CP=x，h为PD边上的高,依题意，△PDQ的面积S可表示为：‎ S=PD·h ………………………………………6分 ‎=(9－x)·x·sin60°‎ ‎=(9x－x2)‎ ‎ =－(x－)2＋. ………………………………………………… 8分 由题意，知0≤x≤5 . ……………………………………………………… 9分 当x=时（满足0≤x≤5），S最大值=. …………………………… 10分 ‎ （3）证法一：如图25-3‎ 假设存在满足条件的点M，则PD必须等于DQ . ………………………… 11分 ‎ 于是9－x=x，x=.‎ ‎ 此时，点P、Q的位置如图25-3所示，连QP .‎ ‎△PDQ恰为等边三角形 .‎ ‎ 过点Q作QM∥DC，交BC于M，点M即为所求.‎ 连结MP，以下证明四边形PDQM是菱形 .‎ 图25-3‎ ‎ 易证△MCP≌△QDP，∴∠D=∠3 . MP=PD ‎ ∴MP∥QD , ∴四边形PDQM是平行四边形 .‎ ‎ 又MP=PD , ∴四边形PDQM是菱形 . ………………………………… 13分 ‎ 所以存在满足条件的点M，且BM=BC－MC=5－=. ………………… 14分 ‎ [注] 本题仅回答存在，给1分.‎ ‎ 证法二：如图25-4‎ 假设存在满足条件的点M，则PD必须等于DQ . ………………………… 11分 ‎ 于是9－x=x，x=. ‎ ‎ 此时，点P、Q的位置如图25-4所示，△PDQ恰为等边三角形 .‎ ‎ 过点D作DO⊥PQ于点O，延长DO交BC于点M，连结PM、QM，则DM垂直平分PQ，∴ MP=MQ .‎ ‎ 易知∠1=∠C .‎ ‎ ∴PQ∥BC .‎ ‎ 又∵DO⊥PQ， ∴MC⊥MD 图25-4‎ ‎ ∴MP= CD=PD ‎ 即MP=PD=DQ=QM ‎ ∴四边形PDQM是菱形 ……………………………………………………… 13分 所以存在满足条件的点M，且BM=BC－MC=5－= ……………… 14分 ‎ [注] 本题仅回答存在，给1分.‎ 1. ‎（南平）如图，平面直角坐标系中有一矩形纸片OABC，O为原点，点A，C分别在x轴，y轴上，点B坐标为（其中m>0），在BC边上选取适当的点E和点F，将ΔOCE沿OE翻折，得到ΔOGE；再将ΔABF沿AF翻折，恰好使点B与点G重合，得到ΔAGF，且∠OGA=900．（1）求m的值；（2）求过点O，G，A的抛物线的解析式和对称轴；（3）在抛物线的对称轴上是否存在点P，使得ΔOPG是等腰三角形？若不存在，请说明理由；若存在，直接答出所有满足条件的点P的坐标（不要求写出求解过程）．‎ ‎ （1）解法一：，‎ 由题意可知，， 2分 ‎， 3分 ‎．又， 4分 解法二：，‎ 由题意可知，， 2分 ‎， 3分 ‎ 4分 ‎（2）解法一：过作直线轴于，‎ 则，，故． 5分 又由（1）知，‎ 设过三点的抛物线解析式为 抛物线过原点，． 6分 又抛物线过两点， 解得 所求抛物线为 8分 它的对称轴为． 9分 解法二：过作直线轴于，‎ 则，，故． 5分 又由（1）知，点关于直线对称，点为抛物线的顶点 6分 于是可设过三点的抛物线解析式为 抛物线过点，，解得 所求抛物线为 8分 它的对称轴为． 9分 ‎（3）答：存在 10分 满足条件的点有，，，．‎ 1. ‎（宁德）如图1，在Rt△ABC中，∠C＝90°，BC＝8厘米，点D在AC上，CD＝3厘米．点P、Q分别由A、C两点同时出发，点P沿AC方向向点C匀速移动，速度为每秒k厘米，行完AC全程用时8秒；点Q沿CB方向向点B匀速移动，速度为每秒1厘米．设运动的时间为x秒（0