初中数学竞赛辅导讲义及习题解答 第15讲 统计的思想方法 10页

1 第十五讲 统计的思想方法 20 世纪 90 年代，美国麻省理工学院教授尼葛洛庞帝写过一本畅销全球的《数字化生存》 一书．事实上，我们的生活、工作离不开数据，要做到心中有数、用数据说话是信息社会对 人的基本要求． 统计学是一门研究如何收集、整理、分析数据，并在此基础上作出推断的科学． 随机抽样与统计推断是统计中最重要的思想方法，也是认识客观世界的事物和现象的方 法之一．即用样本的某种特征去估计总体的相应特征，用样本的平均水平、波动情况、分布 规律等特征估计总体的平均水平、波动情况和分布规律． 【例题求解】 【例 1】 现有 A，B 两个班级，每个班级各有 45 名学生参加一次测验．每名参加者可获 得 0，1，2，3，4，5，6，7，8，9 分这几种不同的分值中的一种．测试结果 A 班的成绩如 下表所示，B 班的成绩如图所示． (1)由观察所得， 班的标准差较大； (2)若两班合计共有 60 人及格，问参加者最少获 分才可以及格． A 班 分数 0 1 2 3 4 5 6 7 8 9 人数 1 3 5 7 6 8 6 4 3 2 思路点拨 对于(2)，数一数两班在某一分数以上的人数即可，凭直觉与估计得出答案． 注： 平均数、中位数、众数都是反映一组数据集中趋势的特征数，但是它们描述集中趋势 的侧重点是不同的： (1)平均数易受数据中少数异常值的影响，有时难以真正反映“平均”； (2)若一组数据有数据多次重复出现，则常用众数来刻画这组数据的集中趋势． 【例 2】 已知数据 1x 、 2x 、 3x 的平均数为 a ， 1y 、 2y 、 3y 的平均数为b ，则数据 11 32 yx  、 22 32 yx  、 33 32 yx  的平均数为( ) A．2a+3b B． ba 3 2 C．6a+9b D．2a+b 思路点拨 运用平均数计算公式并结合已知条件导出新数据的平均数． 2 【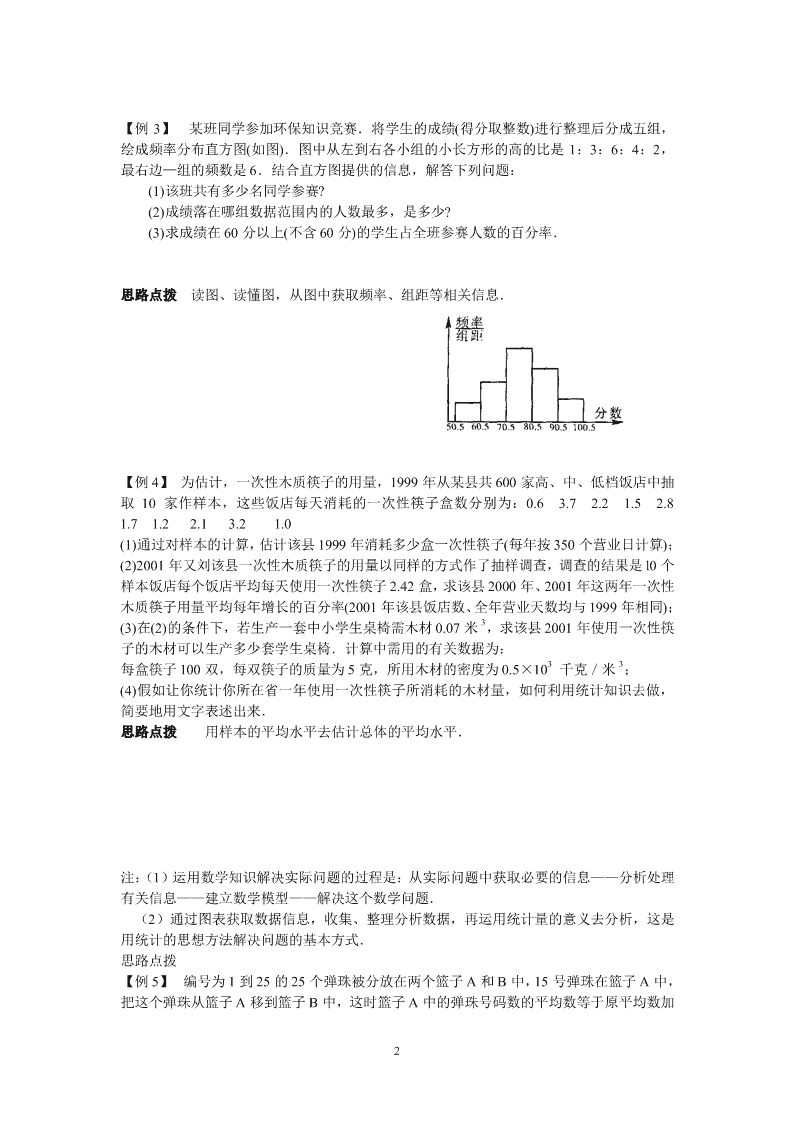例 3】 某班同学参加环保知识竞赛．将学生的成绩(得分取整数)进行整理后分成五组， 绘成频率分布直方图(如图)．图中从左到右各小组的小长方形的高的比是 1：3：6：4：2， 最右边—组的频数是 6．结合直方图提供的信息，解答下列问题： (1)该班共有多少名同学参赛? (2)成绩落在哪组数据范围内的人数最多，是多少? (3)求成绩在 60 分以上(不含 60 分)的学生占全班参赛人数的百分率． 思路点拨 读图、读懂图，从图中获取频率、组距等相关信息． 【例 4】 为估计，一次性木质筷子的用量，1999 年从某县共 600 家高、中、低档饭店中抽 取 10 家作样本，这些饭店每天消耗的一次性筷子盒数分别为：0.6 3.7 2.2 1.5 2.8 1.7 1.2 2.1 3.2 1.0 (1)通过对样本的计算，估计该县 1999 年消耗多少盒一次性筷子(每年按 350 个营业日计算)； (2)2001 年又刘该县一次性木质筷子的用量以同样的方式作了抽样调查，调查的结果是 l0 个 样本饭店每个饭店平均每天使用一次性筷子 2.42 盒，求该县 2000 年、2001 年这两年一次性 木质筷子用量平均每年增长的百分率(2001 年该县饭店数、全年营业天数均与 1999 年相同)； (3)在(2)的条件下，若生产一套中小学生桌椅需木材 0.07 米 3，求该县 2001 年使用一次性筷 子的木材可以生产多少套学生桌椅．计算中需用的有关数据为： 每盒筷子 100 双，每双筷子的质量为 5 克，所用木材的密度为 0.5×103 千克／米 3； (4)假如让你统计你所在省一年使用一次性筷子所消耗的木材量，如何利用统计知识去做， 简要地用文字表述出来． 思路点拨 用样本的平均水平去估计总体的平均水平． 注：（1）运用数学知识解决实际问题的过程是：从实际问题中获取必要的信息——分析处理 有关信息——建立数学模型——解决这个数学问题． （2）通过图表获取数据信息，收集、整理分析数据，再运用统计量的意义去分析，这是 用统计的思想方法解决问题的基本方式． 思路点拨 【例 5】 编号为 1 到 25 的 25 个弹珠被分放在两个篮子 A 和 B 中，15 号弹珠在篮子 A 中， 把这个弹珠从篮子 A 移到篮子 B 中，这时篮子 A 中的弹珠号码数的平均数等于原平均数加 3 4 1 ，B 中弹珠号码数的平均数也等于原平均数加 4 1 ，问原来在篮子 A 中有多少个弹珠? 思路点拨 用字母分别表示篮子 A、B 弹珠数及相应的平均数，运用方程、方程组等知识求 解． 学历训练 1．某校初二年级全体 320 名学生在电脑培训前后各参加了一次水平相同的考试，考分都以 同一标准划分成“不合格”、“合格”、“优秀”三个等级．为了了解电脑培训的效果，用抽签 方式得到其中 32 名学生的两次考试考分等级，所绘制的统计图如图所示．试结合图示信息 回答下列问题： (1)这 32 名学生培训前考分的中位数所在的等级是 ，培训后考分的中位数所在的等 级是 ． (2)这 32 名学生经过培训，考分等级“不合格”的百分比由 下降到 ． (3)估计该校整个初二年级中，培训后考分等级为“合格”与“优秀”的学生共有 名． (4)你认为上述估计合理吗?理由是什么? 答： ，理由 ． 2．某商店 3、4 月份出售同一品牌各种规格的空调销售台数如下表： 根据表中数据回答： (1)商店平均每月销售空调 (台)； (2)商店出售的各种规格的空调中，众数是 (匹)； (3)在研究 6 月份进货时，商店经理决定 (匹)的空调要多进； (匹)的空调要少进． 3．为了了解某中学初三年级 250 名学生升学考试的数学成绩，从中抽取了 50 名学生的数学 成绩进行分析，求得 5.94样本x ．下面是 50 名学生数学成绩的频率分布表： 分 组 频数累计 频数 频率 60．5～70．5 正 3 a 70．5～80．5 正正 6 0．12 80．5～90．5 正正 9 0．18 4 90．5～100．5 正正正正 17 0．34 100．5～110．5 正正 b 0．2 110．5～120．5 正 5 0．1 合 计 50 1 根据题中给出的条件回答下列问题： (1)在这次抽样分析的过程中，样本是 ； (2)频率分布表中的数据 a = ， = ； (3)估计该校初三年级这次升学考试的数学平均成绩约为 分； (4)耷这次升学考试中，该校初三年级数学成绩在 90．5～100．5 范围内的人数约为 人． 4．小明测得一周的体温并登记在下表（单位：℃） 星期 日 一 二 三 四 五 六 周平均体温 体温 36.6 36.7 37.0 37.3 36.9 37.1 36.9 其中星期四的体温被墨迹污染，根据表中数据，可得此日的体温是( ) A．36．?℃ B．36．8℃ C．36．9℃ D．37．0℃ 5．甲、乙两班举行电脑汉字输入速度比赛，参加学生每分钟输入汉字的个数经统计计算后 填入下表： 班级 参加人数 中位数 方差 平均字数 甲 55 149 191 135 乙 55 151 110 135 某同学根据上表分析得出如下结论：①甲、乙两班学生成绩的平均水平相同；②乙班优秀的 人数多于甲班优秀的人数(每分钟输入汉字数≥150 个为优秀)；③甲班的成绩的波动情况比 乙班的成绩的波动大，上述结论正确的是( ) A．①②③ B．①② C．①③ D．②③ 6．今年春季，我国部分地区 SARS 流行，党和政府采取果断措施，防治结合，很快使病情 得到控制．下图是某同学记载的 5 月 1 日至 30 日每天全国的 SARS 新增确诊病例数据图， 将图中记载的数据每 5 天作为一组，从左至右分为第一组至第六组，下列说法：①第一组的 平均数最大，第六组的平均数最小；②第二组的中位数为 138；③第四组的众数为 28；其中 正确的有( ) A．0 个 B．1 个 C．2 个 D．3 个 7．某风景区对 5 个旅游景点的门票价格进行了调整，据统计，调价前后各景点的游客人数 基本不变．有关数据如下表所示： 5 （1）该风景区称调整前后这 5 个景点门票的平均收费不变，平均日总收入持平．问风景区 是怎样计算的？ （2）另一方面，游客认为调整收费后风景区的平均日总收入相对于调价前，实际上增加了 约 9.4%．问游客是怎样计算的？ （3）你认为风景区和游客哪一个的说法较能反映整体实际？ 8．甲、乙两人在相同条件下各射靶 10 次，每次射靶的成绩情况如图所示． （1）请填写下表: 平均数 方差 中位数 命中 9 环以上次数 甲 7 1．2 1 乙 5．4 （2）请从下列四个不同的角度对这次测试结果进行分析. ①从平均数和方差相结合看； ②从平均数和中位数相结合看（分析谁的成绩好些）； ③从平均数和命中 9 环以上次数相结合看（分析谁的成绩好些）； ④从折线图上两人射击命中环数的走势看（分析谁更有潜力）． 9．明湖区一中对初二年级女生仰卧起坐的测试成绩进行统计分析，将数据整理后，画出如 下频率分布直方图，已知图中从左到右的第一、第二、第三、第四、第六小组的频率依次是 0.10、0.15、0.20、0.30、0.05，第五小组的频数是 36，根据所给的图填空： (1)第五小组的频率是 ，请补全这个频率分布图； (2)参加这次测试的女生人数是 ；若次数在24(含24次)以上为达标(此标准为中考 体 育标准)，则该校初二年级女生的达标率为 ． (3)请你用统计知识，以中考体育标准对明湖区十二所中学初二女生仰卧起坐成绩的达标率 作一个估计 ． 6 10．我国于 2000 年 11 月 1 日起进行了第五次全国人口普查的登记工作，据第五次人口普查， 我国每 10 万人中拥有各种受教育程度的人数如下：具有大学程度的为 3611 人；具有高中程 度的为 11146 人；具有初中程度的为 33961 人；具有小学程度的为 35701 人． (1) 根据以上数据填写下表： 受教育程度 每 10 万人中所占百分比( a ％)( a 精确到 0.01) 大学程度 高中程度 初中程度 小学程度 (2)以下各示意图中正确的是( )．(将正确示意图数字代号填在括号内) 11．新华高科技股份有限公司董事会决定今年用 13 亿资金投资发展项目，现有 6 个项目可 供选择(每个项目或者被全部投资，或者不被投资)，各项目所需投资金额和预计年均收益如 下表： 项目 A B C D E F 投资(亿元) 5 2 6 4 6 8 收益(亿元) 0．55 0．4 0．6 0．4 0．9 l 如果要求所有投资的项目的收益总额不得低于 1．6 亿元，那么，当选择的投资项目是 时，投资的收益总额最大． 12．新华社 4 月 3 日发布了一则由国家安全生产监督管理局统计的信息；2003 年 1 月至 2 月全国共发生事故 17 万多起，各类事故发生情况具体统计如下： 事故类型 事故数 量 死亡人数(单 位：人) 死亡人数占各类事故总死亡人数 的百分比 火灾事故(不含森 林草原火灾) 54773 610 铁路路外伤亡事故 1962 1409 工矿企业伤亡事故 1417 1639 道路交通事故 115815 17290 合计 173967 20948 (1)请你计算出各类事故死亡人数占总死亡人数的百分比，填入上表(精确到 0.01)； (2)为了更清楚地表示出问题(1)中的百分比，请你完成下面的扇形统计图； 7 (3)请根据你所学的统计知识提出问题(不需要作解答，也不要解释，但所提的问题应是利用 表中所提供数据能求解的)． 13．将最小的 31 个自然数分成 A、B 两组，10 在 A 组中，如果把 10 从 A 组移到 B 组，则 A 组中各数的算术平均数增加 2 1 ，B 组中各数的算术平均数也增加 2 1 ．问 A 组中原有多少 个数? 14．某次数学竞赛共有 15 道题，下表是对于做对 n ( n =0，1，2…15)道题的人数的一个统 计，如果又知其中做对 4 道题和 4 道以上的学生每人平均做对 6 道题，做对 10 道题和 10 道题以下的学生每人平均做对 4 道题，问这个表至少统计了多少人? n 0 1 2 3 … 12 13 14 15 做对 n 道题的人数 7 8 10 2l … 15 6 3 l 8 参考答案 9 10