2020年秋人教版 九年级数学上册期中复习 试卷（无答案） 7页

九年级上册期中考试 一、选择题 1.若关于 x 的方程 x2-x＋k＝0 没有实数根，则（ ） A.k＜ B.k ＞ C. k≤ D. k≥ 2.把二次函数 y＝－1 4x2－x＋3 用配方法化成 y＝a(x－h)2＋k 的形式(　　) A．y＝－1 4(x－2)2＋2 B．y＝1 4(x－2)2＋4 C．y＝－1 4(x＋2)2＋4 D．y＝(1 2x－1 2)2＋3 3.下列语句中不正确的有（ 　 ） ①相等的圆心角所对的弧相等；②平分弦的直径垂直于弦；③圆是轴对称图形，任何一 条直径都是它的对称轴；④半圆是弧． A．1 个 Ｂ．2 个 C．3 个 Ｄ．4 个 4.若关于 的方程 有实数解，则 得取值范围是____ A. B. C. D. 5. 如图二次函数 y＝2x2＋mx＋8 的图象，则 m 的值是(　　) A．－8 B．8 C．±8 D．6 6.如图，⊙O 的直径 AB=10，CD 是⊙O 的弦，CD⊥AB，垂足为 E，且 BE：AE=1：4，则 4 1 4 1 4 1 x 23( 4)x k− = k 0k > 0k < 0k ≤ 0k ≥ CD 的长为（ ） A．10 B．12 C．8 D．9 7.受非洲猪瘟及其他因素影响，2019 年 9 月份猪肉价格两次大幅度上涨，瘦肉价格由原来 23 元/千克，连续两次上涨 x%后，售价上升到 60 元/千克，则下列方程中正确的是（　　） A．23（1﹣x%）2＝60 B．23（1+x%）2＝60 C．23（1+x2%）＝60 D．23（1+2x%）＝60 8.如图二次函数 y＝ax2＋bx＋c(a≠0)的图象，下列结论正确的是(　　) A．a<0 B．b2－4ac<0 C．当－10 D．－ b 2a＝1 9.如图， 是 的切线，切点分别是 ．若 ，则 的 长是( ) A．2 B．4 C．6 D．8 , ,AB AC BD O , ,P C D 5, 3AC BD= = AB 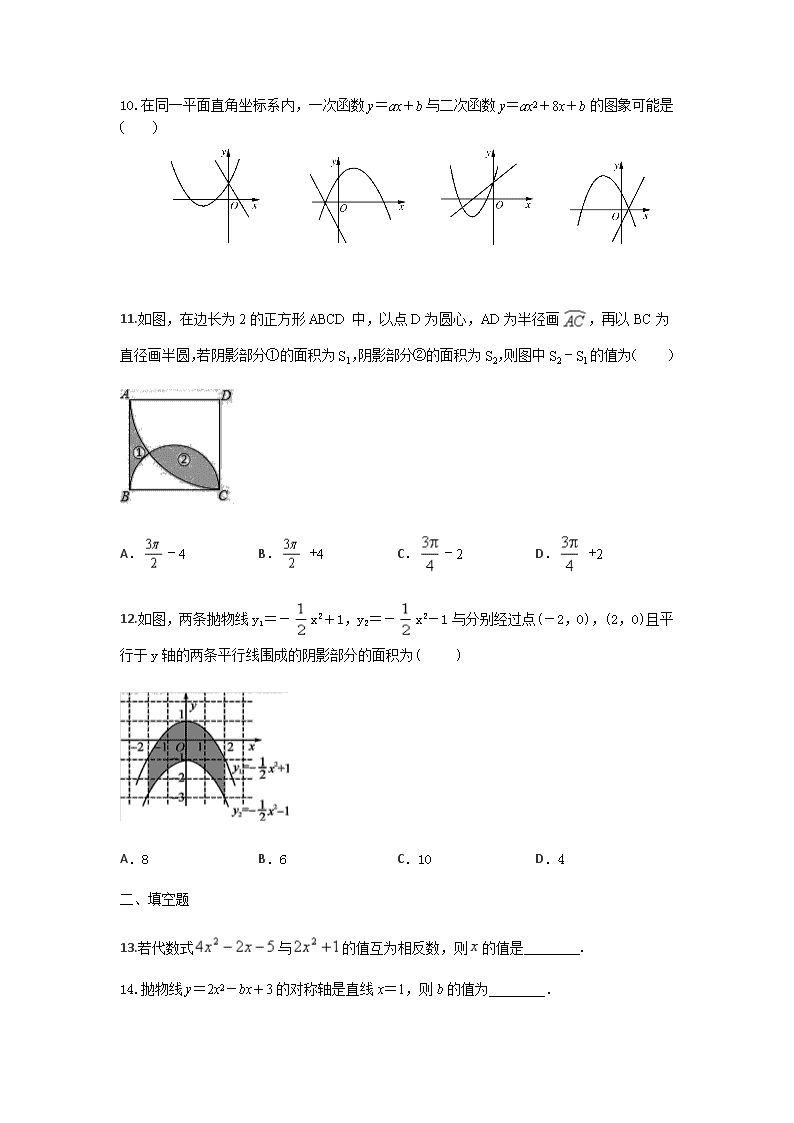10.在同一平面直角坐标系内，一次函数 y＝ax＋b 与二次函数 y＝ax2＋8x＋b 的图象可能是 (　　) 11.如图，在边长为 2 的正方形 ABCD 中，以点 D 为圆心，AD 为半径画 ，再以 BC 为 直径画半圆，若阴影部分①的面积为 S1，阴影部分②的面积为 S2，则图中 S2﹣S1 的值为（　　） A． ﹣4 B． +4 C． ﹣2 D． +2 12.如图，两条抛物线 y1＝－ x2＋1，y2＝－ x2－1 与分别经过点(－2，0)，(2，0)且平 行于 y 轴的两条平行线围成的阴影部分的面积为(　 　) A．8 B．6 C．10 D．4 二、填空题 13.若代数式 与 的值互为相反数，则 的值是 . 14.抛物线 y＝2x2－bx＋3 的对称轴是直线 x＝1，则 b 的值为________． 524 2 −− xx 12 2 +x x AC 3 2 π 3 2 π 3 4 π 3 4 π 1 2 1 2 15.一个点到圆的最小距离为 ，最大距离为 ，则该圆的半径是____________． 16.已知 m 是方程式 x2+x﹣1＝0 的根，则式子 m3+2m2+2019 的值为　 　． 17.如图，已知二次函数 y＝ax2＋bx＋c 的图象与 x 轴交于 A(1,0)，B(3,0)两点，与 y 轴 交于点 C(0,3)，则二次函数的图象的顶点坐标是________． 18.如图，已知 P、Q 分别是⊙O 的内接正六边形 ABCDEF 的边 AB、BC 上的点，AP=BQ， 则∠POQ 的度数为___°． 19.如图，在正方形 ABCD 中，E 为 BC 边上的点，F 为 CD 边上的点，且 AE＝AF，AB ＝4，设 EC＝x，△AEF 的面积为 y，则 y 与 x 之间的函数关系式是__________． 20.如图，在扇形 AOB 中， ，半径 OC 交弦 AB 于点 D，且 ．若 ，则阴影部分的面积为_____． 三、解答题 3cm 8cm 120AOB °∠ = OC OA⊥ 2 3=OA 21.解下列方程: (1)2 x2＋x－6＝0； (2) x2＋4x＝2； (3)5x2－4x－12＝0； (4)4x2＋4x＋10＝1－8x. 22.求经过 A(1,4)，B(－2,1)两点，对称轴为 x＝－1 的抛物线的解析式． 23.已知：如图，在⊙O 中，弦 CD 与直径 AB 相交于点 E，∠BED＝60°，DE＝OE＝4． 求：（1）CE 的长； （2）⊙O 的半径． 24.某中学课外兴趣活动小组准备围建一个矩形苗圃，其中边靠墙，另外三边用长为 30 米的 篱笆围成．已知墙长为 18 米（如图所示），设这个苗圃垂直于墙的一边长为 x 米． （1）若苗圃的面积为 72 平方米，求 x 的值； （2）这个苗圃的面积能否是 120 平方米？请说明理由． 25.如图，△ABC 内接于⊙O，∠B=60°，CD 是⊙O 的直径，点 P 是 CD 延长线上的一点， 且 AP=AC． 试求：（1）求证：PA 是⊙O 的切线； （2）若 PD=3，求⊙O 的直径 26.已知，如图抛物线 y＝ax2＋3ax＋c(a>0)与 y 轴交于点 C，与 x 轴交于 A，B 两点，点 A 在点 B 左侧．点 B 的坐标为(1,0)，OC＝3OB. (1)求抛物线的解析式； (2)若点 D 是线段 AC 下方抛物线上的动点，求四边形 ABCD 面积的最大值； (3)若点 E 在 x 轴上，点 P 在抛物线上．是否存在以 A，C，E，P 为顶点且以 AC 为一 边的平行四边形？若存在，求点 P 的坐标；若不存在，请说明理由．