2019九年级数学上册 第一章 特殊平行四边形 1菱形的性质和判定 6页

菱形的性质和判定 课 题 菱形的性质和判定（三）‎ 课时安排 共（3 ）课时 课程标准 ‎ 课标P34 运用菱形的性质和判定定理解决问题.‎ 学习目标 ‎1.能灵活运用菱形的性质定理及判定定理解决一些相关问题，并掌握菱形面积的求法.‎ ‎2.经历菱形性质定理及判定定理的应用过程，体会数形结合、转化等思想方法.‎ 教学重点 目标1,2‎ 教学难点 目标2‎ 教学方法 支架式教学法，教师引导 教学准备 希沃白板，课件 课前作业 1. 复习回顾菱形的性质和判定定理.‎ 教学过程 教学环节 课堂合作交流 二次备课 ‎（修改人： ）‎ 环 节 一 ‎1.复习回顾 ‎1.在菱形ABCD中，AB=6，请回答下列问题：‎ ‎(1)其余三条边AD、DC、BC的长度分别是多少？‎ ‎(2)对角线AC与BD有什么位置关系？‎ ‎(3)若∠ADC=120°，求AC的长.‎ ‎2.在□ABCD中添加一个条件使其成为菱形：‎ 添加方式1： .‎ 添加方式2： .‎ 通过一些简单题目的设计，帮助学生回顾菱形的相关性质及判定方法，学生从题目入手，不会显得那么古板枯燥，不仅能回顾相关知识而且能激发学生学习兴趣.‎ 6‎ 二、知识应用 例3 如图3，四边形ABCD是边长为‎13cm的菱形，其中对角线BD长为‎10cm.求：(1)对角线AC的长度；‎ ‎(2)菱形ABCD的面积.‎ 解：(1)∵四边形ABCD是菱形，‎ E ‎∴AC⊥BD,即∠AED=90°，‎ DE= BD=5（cm）‎ ‎∴在Rt△ADE中，由勾股定理可得：‎ ‎∴AC=2AE=2×12=24(cm).‎ ‎（2）S菱形ABCD= S△ABD+ S△CBD ‎=2×S△ABD=2××BD×AE ‎= BD×AE=10×12=120(cm2).‎ 通过例3让学生对菱形的相关性质进行灵活应用，同时学生对于具体的问题通过自主思考、小组交流、学生展讲、教师点拨后基本能形成比较好的解题思路.‎ 课中作业 追问(1)菱形的面积和对角线有什么关系？‎ 环 节 二 ‎（1）菱形的面积和对角线有什么关系？‎ ‎ 菱形的面积等于两条对角线乘积的一半.‎ ‎（引起学生的思考，进而突破这一教学难点）‎ ‎(2)拓展：对角线互相垂直的四边形面积等于其两条对角线乘积的一半.‎ ‎（留作课下证明）‎ 变式训练 如上图3，四边形ABCD是菱形，其中对角线BD长为‎12cm，AC长为‎16cm.‎ 6‎ 求：‎ ‎(1)菱形的边长；‎ ‎(2)求菱形一条边上的高.‎ 让学生更加深入地掌握菱形的相关性质，同时对于第二问，学生必须灵活运用菱形的面积等于对角线乘积的一半，这一结论求出面积进而求出一边上的高.‎ 课中作业 方法启迪：‎ 同学们，在我们刚才完成的例题及变式训练中你有什么方法感悟或者经验？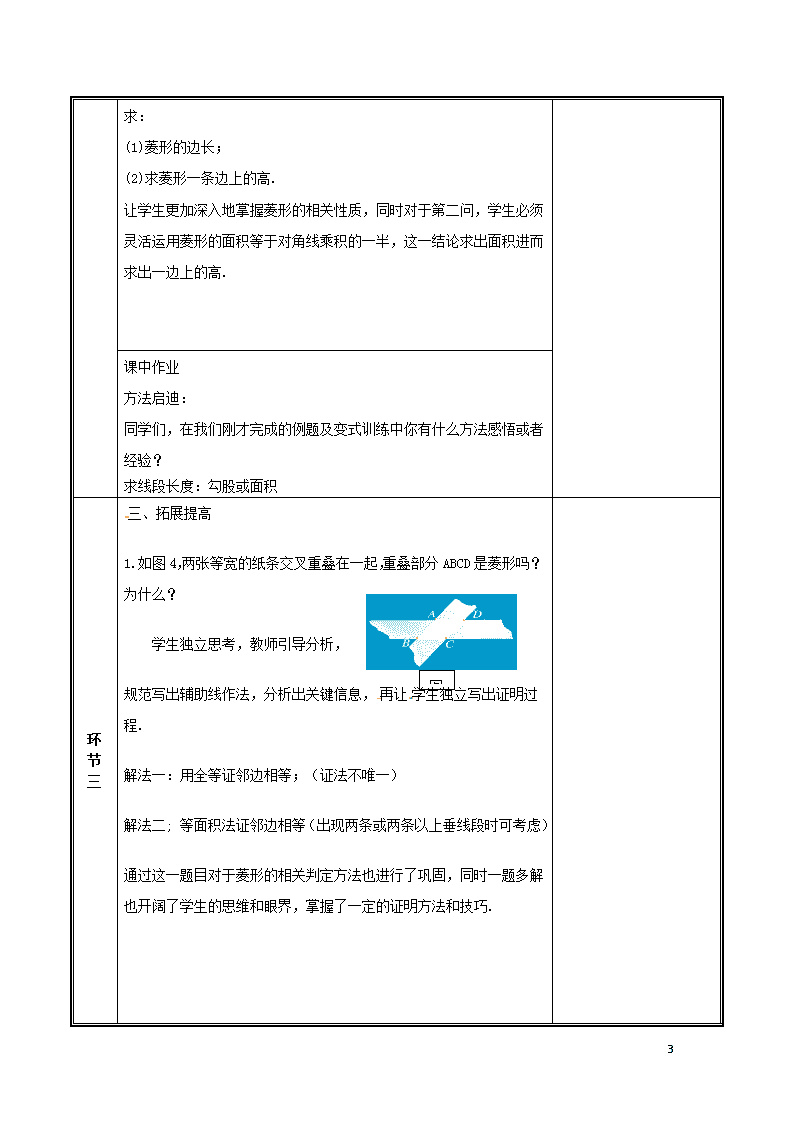‎ 求线段长度：勾股或面积 环 节 三 三、拓展提高 图4‎ ‎1.如图4，两张等宽的纸条交叉重叠在一起，重叠部分ABCD是菱形吗？为什么？‎ ‎ 学生独立思考，教师引导分析，‎ 规范写出辅助线作法，分析出关键信息，再让学生独立写出证明过程.‎ 解法一：用全等证邻边相等；（证法不唯一）‎ 解法二; 等面积法证邻边相等（出现两条或两条以上垂线段时可考虑）‎ 通过这一题目对于菱形的相关判定方法也进行了巩固，同时一题多解也开阔了学生的思维和眼界，掌握了一定的证明方法和技巧.‎ 6‎ ‎ ‎ 四、课堂小结 本节课你学到了什么？‎ 课中作业 自我检测 ‎1.如图1所示，菱形ABCD的周长为‎40cm，它的一条对角线BD长‎10cm，则（1）∠ABC= °，AC= .‎ ‎ （2）菱形ABCD的面积是___________‎ ‎2.已知，如图2，在四边形ABCD中，AD=BC，点E、F、G、H分别是AB、CD、AC、BD的中点，四边形EGFH是（ ）‎ ‎ A.矩形 B.菱形 C.等腰梯形 D.正方形 图1‎ ‎3.如图3， 在四边形ABCD中，AD∥BC，E为BC的中点，BC＝2AD，EA＝ED＝2，AC与ED相交于点F．当AB与AC具有什么位置关系时，四边形AECD是菱形？请说明理由，并求出此时菱形AECD的面积．‎ ‎ ‎ 图3‎ 6‎ ‎           ‎ 课后作业设计： ‎ ‎1.课本P9 习题1.3 1-4题 必做 ‎2.《全品学练考》作业手册 P5 1-7题（必做） ‎ ‎ 其余选做 ‎ ‎（修改人： ）‎ 板书设计：‎ 菱形的性质和判定（三）‎ 一、 菱形的面积等于两条对角线乘积的一半.‎ 菱形的面积等于底*高 二、例题规范解法 教学反思：‎ ‎ 1.重视课本提供资源，有效进行合理整合 ‎ 新教材的编订都是相关专家经过深思熟虑才编写出来的，教师在使用教材时，一定要深入钻研教材的每一个题目、每一句话，不要轻易舍弃，同时也要重视学情，根据实际情况对教材进行合理搭配，比如在本节课中我对典型例题进行了变式训练，这其实是把课后题提前到这一位置，并通过有效追问把本节课学生不易掌握的菱形面积的求法不失时机地进行了夯实，起到了较好的效果.‎ ‎ 2.让每一个学生都能有所收获 6‎ ‎ 本节课是菱形的第三课时，学生的学习差异是非常大的，有些学生不用老师讲解本节课已经掌握差不多了，还有一些学生在前两节课的学习中就积累了很多的问题，本节课要提升就会出现很多的困难，如何解决这一难题呢？在实际教学中我注意了分层教学，设计中有两个环节来体现，一是针对优生的知者加速，一是针对学困生的补读帮困，两个环节的设置兼顾到了每一个层次的学生，让课堂效率进一步得到了提升.‎ ‎ 3.规范答题，重视学生的反思过程 ‎ 学生对于几何题的规范答题是在课堂上需要重点强调的，这也是培养学生严谨细致的数学素养的一个手段，同时在教学中应注意学生解题的反思过程，例如由例题及变式训练完成反思过程后，学生的思维得到了升华，同时对于同类题目的突破方式有了初步的框架，对于以后的学习是一个促进，本质上讲学习就是在学生不断反思中完成的.‎ 6‎