江苏省南京市联合体学校2020-2021学年九年级（上）期中数学试题（有答案） 12页

‎2020～2021学年度第一学期期中学情调研 九年级数学 注意事项:‎ ‎1．本试卷共6页．全卷满分120分．考试时间为120分钟．考生答题全部答在答题卡上，答在本试卷上无效．‎ ‎2．请认真核对监考教师在答题卡上所粘贴条形码的姓名､考试证号是否与本人相符合，再将自己的姓名､准考证号用0.5毫米黑色墨水签字笔填写在答题卡及本试卷上．‎ ‎3．答选择题必须用2B铅笔将答题卡上对应的答案标号涂黑．如需改动，请用橡皮擦干净后，再选涂其他答案．答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡上的指定位置，在其他位置答题一律无效．‎ ‎4．作图必须用2B铅笔作答，并请加黑加粗，描写清楚．‎ 一、选择题(本大题共6小题，每小题2分，共12分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上)‎ ‎1．下列方程中，是关于x的一元二次方程的是 A．2x＋y＝2 B．x＋y2＝0 C．ax2＋bx＋c＝0 D．2x－x2＝1‎ ‎2．若圆弧的半径为3，所对的圆心角为60°，则弧长为 A． π B．π C．π D．3π ‎3．反映一组数据变化范围的是 ‎ A．极差 B．方差 C．众数 D．平均数 ‎4．下列方程中，两个实数根的和为0的是 ‎ A．x2－x＝0 B．x2＋2x＝0 C．x2－1＝0 D．x2－2x＋1＝0‎ ‎5．某校九年级（1）班部分学生上学路上所花的时间如图所示．‎ 设他们上学路上所花时间的平均数为a，中位数为b，众数 为c，则有 A．b＞a＞c B．c＞a＞b C．a＞b＞c D．b＞c＞a ‎ ‎6．如图，AC为半圆的直径，弦AB＝3，∠BAC＝30°，点E、F 分别为AB和AC上的动点，则BF＋EF的最小值为 A． B． ‎ 九年级数学试卷第 12 页 共 6 页 C．3 D．＋ 二、填空题(本大题共10小题，每小题2分，共20分．不需写出解答过程，请把答案直接填写在答题 卡相应位置上)‎ ‎7．方程x2－4＝0的解是 ▲ ．‎ ‎8．若⊙O的半径为3cm，点A与圆心O的距离为4cm，则点A与⊙O的位置关系是 ▲ ．‎ ‎9．若关于x的一元二次方程x2＋4x＋k＝0有两个相等的实数根，则k＝ ▲ ．‎ ‎10．某招聘考试分笔试和面试两项，笔试按60%、面试按40%计算总成绩．若李明笔试成绩为90分，‎ 面试成绩为85分，则李明的总成绩是 ▲ 分．‎ ‎11．将方程x2＋6x－3＝0化为(x＋h)2＝k的形式是 ▲ ．‎ ‎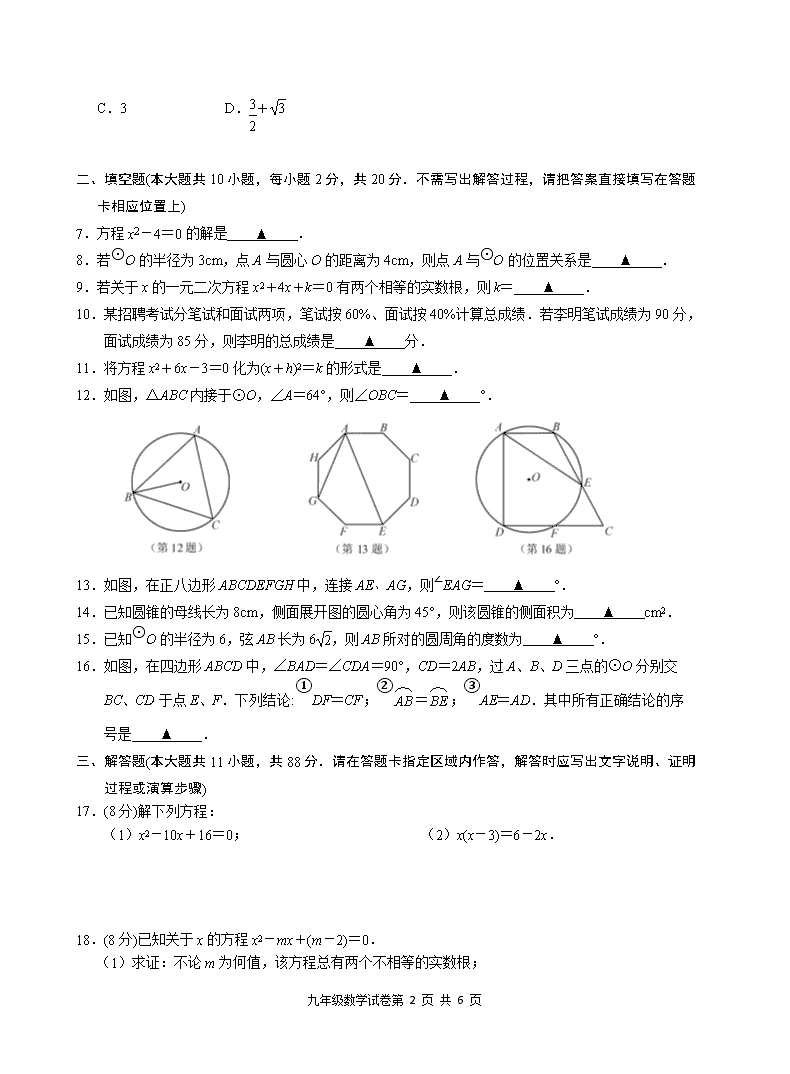12．如图，△ABC内接于⊙O，∠A＝64°，则∠OBC＝ ▲ °．‎ ‎13．如图，在正八边形ABCDEFGH中，连接AE、AG，则∠EAG＝ ▲ °．‎ ‎14．已知圆锥的母线长为8cm，侧面展开图的圆心角为45°，则该圆锥的侧面积为 ▲ cm2．‎ ‎15．已知⊙O的半径为6，弦AB长为6，则AB所对的圆周角的度数为 ▲ °．‎ ‎16．如图，在四边形ABCD中，∠BAD＝∠CDA＝90°，CD＝2AB，过A、B、D三点的⊙O分别交 BC、CD于点E、F．下列结论:①DF＝CF；②＝；③AE＝AD．其中所有正确结论的序 号是 ▲ ．‎ 三、解答题(本大题共11小题，共88分．请在答题卡指定区域内作答，解答时应写出文字说明、证明 过程或演算步骤)‎ ‎17．(8分)解下列方程：‎ ‎（1）x2－10x＋16＝0 ； （2）x(x－3)＝6－2x．‎ ‎18．(8分)已知关于x的方程x2－mx＋(m－2)＝0．‎ ‎（1）求证：不论m为何值，该方程总有两个不相等的实数根；‎ 九年级数学试卷第 12 页 共 6 页 ‎（2）若方程有一个根是2，求m的值以及方程的另一个根．‎ ‎19．(8分)甲、乙两名同学本学期的五次数学测试成绩如下（单位：分）:‎ 第1次 第2次 第3次 第4次 第5次 甲 ‎86‎ ‎83‎ ‎90‎ ‎80‎ ‎86‎ 乙 ‎78‎ ‎82‎ ‎84‎ ‎89‎ ‎92‎ ‎（1）完成下表:‎ 中位数 平均数 方差 甲 ‎ ▲ ‎ ‎85‎ ‎ ▲ ‎ 乙 ‎84‎ ‎85‎ ‎24.8‎ ‎（2）请运用所学的统计知识，从两个不同角度评价甲、乙两人的数学成绩．‎ ‎20．(6分)已知某企业2020年3月份的口罩产量是500万只，4月份的产量比3月份有所增长．5月份 新冠疫情有所好转，口罩产量降为420万只．若两次产量变化的百分率相同，求这个百分率．‎ ‎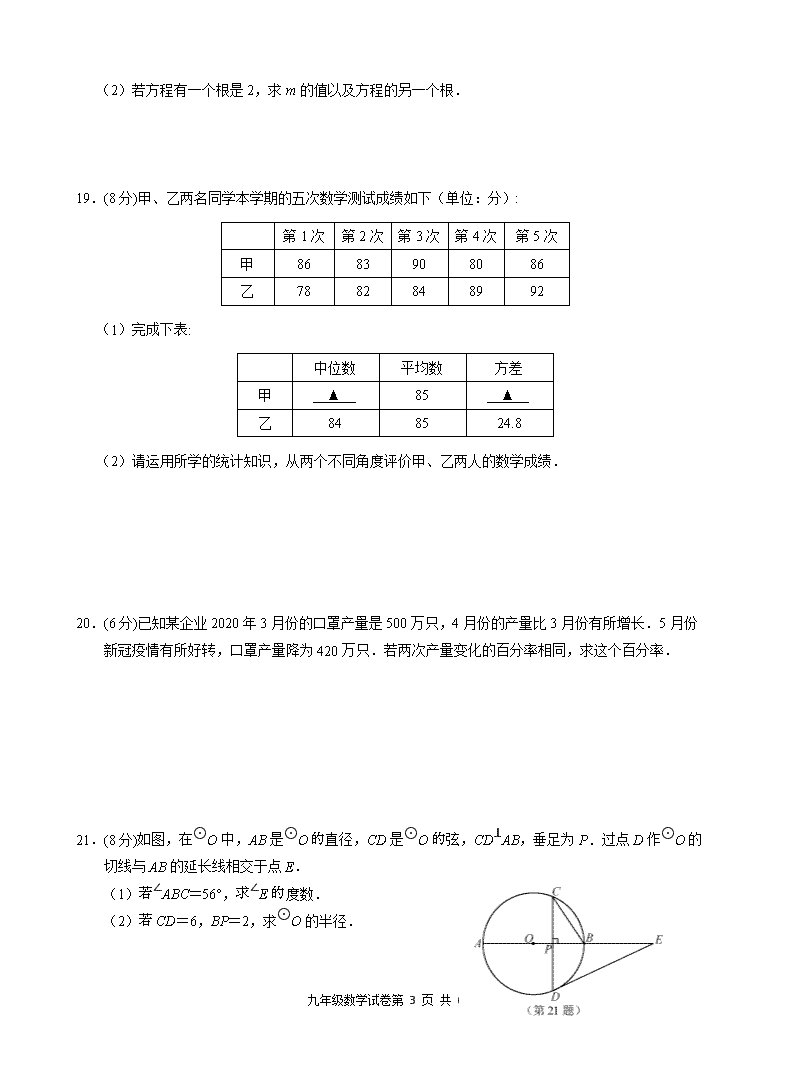21．(8分)如图，在⊙O中，AB是⊙O的直径，CD是⊙O的弦，CD⊥AB，垂足为P．过点D作⊙O的 切线与AB的延长线相交于点E．‎ ‎（1）若∠ABC＝56°，求∠E的度数．‎ ‎（2）若CD＝6，BP＝2，求⊙O的半径．‎ 九年级数学试卷第 12 页 共 6 页 ‎22．(8分)如图，有一道长为10m的墙，计划用总长为54m的篱笆，靠墙围成由六个小长方形组成的 矩形花圃ABCD．若花圃ABCD面积为72m2，求AB的长．‎ ‎23．(6分)如图，在⊙O中，C是的中点，∠C＝∠AOB．‎ 求证：四边形OACB是菱形．‎ ‎24．(8分)如图，PM是⊙O的切线，切点是A．点B、C、D是⊙O上的点，PA＝PB．‎ ‎（1）求证PB是⊙O的切线；‎ ‎（2）若∠C＝92°，∠MAD＝40°，则∠P＝ ▲ °．‎ 九年级数学试卷第 12 页 共 6 页 ‎25．(8分)某商店经销的某种商品，每件成本为30元．经市场调研，售价为40元时，可销售200件；‎ 售价每增加2元，销售量将减少20件．如果这种商品全部销售完，该商店可盈利2250元，那么 该商品每件售价多少元？‎ ‎26．（10分）如图，在矩形ABCD中，AB＝4，BC＝6．点E为CD边上的一个动点（不与C、D重合），‎ ‎⊙O是△BCE的外接圆．‎ ‎（1）若CE＝2，⊙O交AD于点F、G，求FG的长度．‎ ‎（第26题）‎ ‎（2）若CE的长度为m，⊙O与AD的位置关系随着m的值变化而变化，试探索⊙O与AD的位置关系及对应的m的取值范围．‎ 九年级数学试卷第 12 页 共 6 页 ‎27．（10分）‎ ‎（1）如图①，AB是⊙O的直径，点C、D在⊙O上，且BC＝BD，CD＝AD．‎ 求证∠ADC＝2∠BDC．‎ ‎（2）如图②，AB是⊙O的直径，点C在⊙O上．若点D是平面内任意一点，且满足AD＝CD，‎ ‎∠ADC＝2∠BDC ．‎ ①利用直尺和圆规在图②中作出所有满足条件的点D（保留作图痕迹，不写作法）． ‎ ②若AB＝4，BC长度为m（0＜m＜4），点D的个数随着m的值变化而变化，直接写出点D的个数及对应的m的取值范围．‎ 九年级数学试卷第 12 页 共 6 页 九年级数学试卷第 12 页 共 6 页 ‎2020～2021学年度第一学期期中学情分析样题 九年级数学参考答案及评分标准 说明：本评分标准每题给出了一种或几种解法供参考，如果考生的解法与本解答不同，参照本评分标准的精神给分．‎ 一、选择题（每小题2分，共计12分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ 答案 D B A C ‎ A B 二、填空题（每小题2分，共计20分）‎ ‎7．x＝±2‎ ‎8．圆外 ‎9．4‎ ‎10．88‎ ‎11．(x+3)2＝12‎ ‎12．26‎ ‎13．45‎ ‎14．8π ‎15．45或135‎ ‎16．①③‎ 三、解答题（本大题共11小题，共计88分）‎ ‎17．（本题8分）‎ ‎（1）解：x2－10x＋25＝9， 1分 ‎(x－5)2＝9， 2分 ‎ x－5＝±3，‎ ‎ x1＝8，x2＝－2． 4分 ‎（2）解：x（x－3）＝－2（x－3）， ……………………………………………… 5分 x（x－3）＋2（x－3）＝0， ‎ ‎(x－3)( x＋2)＝0， 6分 x1＝3，x2＝－2． 8分 ‎18．（本题8分）‎ ‎（1）证明：∵a=1，b=－m，c= m－2 1分 ‎∴b 2－4ac=(－m )2－4×1×8（m－2）=m 2－4m+8=（m－2）2+4 2分 ‎∵(m－2)2≥0，∴(m－2)2+4＞0 3分 ‎∴不论m为何值，该方程都有两个不相等的实数根． 4分 ‎（2）根据题意：22－2 m+（m－2）＝0，∴m=2． 6分 ‎ 则x2－2x＝0，∴x1＝0，x2＝2．‎ ‎ ∴m的值为2，另一个根为0． 8分 ‎19．（本题8分）‎ ‎（1）85，11.2 4分 ‎（2）数据的集中程度：①从中位数看，甲的中位数略大于乙的中位数，说明甲的数学成绩略好于乙；‎ 数据的离散程度：②从方差看，甲的方差小于乙的方差，且两人的平均成绩相同，说明甲的成绩比乙更稳定；‎ 数据的变化趋势：③从两人成绩的变化趋势看，乙的成绩在逐渐上升，说明乙的成绩进步较大。 8分 ‎（注：写出其中两个即可，其它情况酌情赋分）‎ ‎20．（本题6分）‎ ‎ 解：设这个百分率是x． ‎ 根据题意，得500 (1＋x)(1－x)＝420． 4分 解这个方程，得x1＝0.4，x2＝－0.4（不合题意，舍去）．‎ 答：这个百分率是40%． 6分 九年级数学试卷第 12 页 共 6 页 ‎21．（本题8分）‎ ‎（1）解：连接OD．‎ ‎ ∵ 在⊙O中，弦AB⊥CD，垂足为P，‎ ‎ ∴∠CPB＝90°．‎ ‎∵∠ABC＝56°，‎ ‎∴∠PCB＝90°－56°＝34°， 1分 ‎∴∠EOD＝2∠CPB＝68°． 2分 ‎∵DE是⊙O的切线．‎ ‎∴∠ODE＝90°， 3分 在Rt△ODE中，∠E＝90°－68°＝22°． 4分 ‎（2）∵ 在⊙O中，弦AB⊥CD，垂足为P，‎ ‎∴ CP＝DP＝CD＝3． 5分 ‎ 设⊙O的半径为r．‎ ‎ 在Rt△ODP中，PD2＋OP2＝OD2，‎ ‎ 即32＋(r－2) 2＝r 2． 7分 ‎ 解方程，得r＝．‎ ‎ 所以⊙O的半径为． 8分 ‎22．（本题8分）‎ 解：设AB的长是xm，则BC的长是（18－x)m． ‎ 根据题意，得x (18－x)＝72． 5分 解这个方程，得x1＝6，x2＝12 7分 当x＝6时，18－x＝12>10（不合题意，舍去）．‎ 当x＝12时，18－x＝6符合题意．‎ 答：AB的长是12m． 8分 ‎23．（本题6分）‎ ‎ 证明：如图，连接OC． ‎ ‎∵C是的中点，‎ ‎∴＝，∴ AC＝BC， 1分 ‎∵在△AOC和△BOC中，AC＝BC，OA＝OB，OC＝OC，‎ ‎∴△AOC≌△BOC． 2分 ‎∴∠ACO＝∠BCO＝∠ACB，∠AOC＝∠BOC＝∠AOB．‎ 又∵∠ACB＝∠AOB． ‎ ‎∴∠ACO＝∠BCO＝∠AOC＝∠BOC． 4分 ‎∴AC＝BC＝OC＝OA＝OB， 5分 ‎∴四边形OACB是菱形． 6分 ‎ ‎ 九年级数学试卷第 12 页 共 6 页 ‎24．(本题8分)‎ ‎ （1）证明：如图，连接OA，OB，OP． ‎ ‎∵PM是⊙O的切线 ‎∴∠PAO＝90° 1分 ‎∵在△PBO和△PAO中，PA＝PB，OA＝OB，OP＝OP，‎ ‎∴△PBO≌△PAO． 3分 ‎∴∠PBO＝∠PAO＝90° 4分 ‎∵点B在⊙O上， 5分 ‎∴PB是⊙O的切线． 6分 ‎（2）76 8分 ‎25．(本题8分)‎ 解：设该商品每件售价x元．‎ ‎ 根据题意，得(x－30)[200－10(x－40)]＝2 250． 5分 ‎ 解这个方程，得x1＝x2＝45． 7分 ‎ 答：该商店每件售价45元． 8分 ‎ ‎26．（本题10分）‎ ‎ （1） 解：过点O作OM⊥FG于点M，延长MO交BC于点N，连接OG，‎ A B C D E O G F M N ‎∵四边形ABCD是矩形，‎ ‎∴∠C＝∠D＝90°，‎ ‎∴BE是⊙O的直径． ‎ ‎∵∠C＝∠D＝∠DMN＝90°，‎ ‎∴四边形MNCD是矩形，‎ ‎∴MN⊥BC，MN＝CD＝AB＝4，‎ ‎∴BN＝CN．‎ ‎∵OB＝OE，‎ ‎∴ON是△BCE的中位线，‎ ‎∴ON＝CE＝1， …………………………… 1分 OM＝4－1＝3． …………………………………………………2分 在Rt△BCE中，BE＝＝2，‎ ‎∴OG＝BE＝．………………………………………………………………… 3分 在Rt△OMG中，MG＝＝1 ………… ……………………………… 4分 ‎∴FG＝2MG＝2． ……………………………………………………………… 5分 ‎（2）‎A B C D A B C D E M N O 九年级数学试卷第 12 页 共 6 页 解：如图，当⊙O与AD相切于点M时，连接OM并反向延长交BC于点N．‎ 由（1）易得ON＝CE＝m，OB＝OM＝4－m，BN＝3，‎ 在Rt△BON中，ON2＋BN2＝OB2，即(m)2＋32＝(4－m)2，解得m＝．……… 7分 ‎∴当0＜m＜时，⊙O与AD相离；……………………………………………… 8分 当m＝时，⊙O与AD相切； ……………………………………………… 9分 ‎（1）‎ A B C D O E F 当＜m＜4时，⊙O与AD相交．……………………………………………… 10分 ‎27．(本题10分)‎ ‎（1）证明：连接AC、OC，作直径DE，交AC于点F，‎ ‎∵AD＝CD，OA＝OC，‎ ‎∴点D、O在AC的垂直平分线上，DE⊥AC，‎ ‎∴＝ ……………………………1分 ‎∴∠ADC＝2∠EDC， ……………………………… 2分 ‎∵AB是⊙O的直径，‎ ‎∴∠ACB＝90°，‎ ‎∴∠ACB＝∠AFD＝90°，‎ ‎∴DF∥BC，……………………………………………………………………3分 ‎∴∠EDC＝∠BCD． ‎ ‎∵BC＝BD，‎ 备用图 O m m m m ‎∴∠BDC＝∠BCD，……………………………………………………………………4分∴∠ADC＝2∠BDC．……………………………………………………………………5分 A B C O D D ‎（2）解：①如图（2），两个点D即为所求；（画图2分）‎ ‎（2）‎ ‎②当0＜m＜时，点D的个数为0；………………………………………………8分 当m＝时，点D的个数为1； …………………………………………………9分 九年级数学试卷第 12 页 共 6 页 当＜m＜4时，点D的个数为2．………………………………………………10分 九年级数学试卷第 12 页 共 6 页