2013年中考数学复习专题讲座2：新概念型问题(含答案) 22页

1 2013年中考数学专题讲座二：新概念型问题 一、中考专题诠释 所谓“新概念”型问题，主要是指在问题中概念了中学数学中没有学过的一些概念、新运 算、新符号，要求学生读懂题意并结合已有知识、能力进行理解，根据新概念进行运算、推 理、迁移的一种题型.“新概念”型问题成为近年来中考数学压轴题的新亮点.在复习中应重视 学生应用新的知识解决问题的能力 二、解题策略和解法精讲 “新概念型专题”关键要把握两点：一是掌握问题原型的特点及其问题解决的思想方法； 二是根据问题情景的变化，通过认真思考，合理进行思想方法的迁移． 三、中考典例剖析 考点一：规律题型中的新概念 例 1 （2012•永州）我们把按照一定顺序排列的一列数称为数列，如 1，3，9，19，33，… 就是一个数列，如果一个数列从第二个数起，每一个数与它前一个数的差等于同一个常数， 那么这个数列就叫做等差数列，这个常数叫做这个等差数列的公差．如 2，4，6，8，10 就 是一个等差数列，它的公差为 2．如果一个数列的后一个数与前一个数的差组成的新数列是 等差数列，则称这个数列为二阶等差数列．例如数列 1，3，9，19，33，…，它的后一个数 与前一个数的差组成的新数列是 2，6，10，14，…，这是一个公差为 4 的等差数列，所以， 数列 1，3，9，19，33，…是一个二阶等差数列．那么，请问二阶等差数列 1，3，7，13，… 的第五个数应是 ． 思路分析：由于 3-1=2，7-3=4，13-7=6，…，由此得出相邻两数之差依次大 2，故 13 的后 一个数比 13 大 8． 解答：解：由数字规律可知，第四个数 13，设第五个数为 x， 则 x-13=8，解得 x=21，即第五个数为 21， 故答案为：21． 点评：本题考查了数字变化规律类问题．关键是确定二阶等差数列的公差为 2． 对应训练 1．（ 2012•自贡）若 x 是不等于 1 的实数，我们把 1 1 x 称为 x 的差倒数，如 2 的差倒数是 1 12 =-1，-1 的差倒数为 1 1 ( 1) = 1 2 ，现已知 x1=- 1 3 ，x2 是 x1 的差倒数，x3 是 x2 的差 倒数，x4 是 x3 的差倒数，…，依次类推，则 x2012= ． 考点二：运算题型中的新概念 例 2 （2012•菏泽）将 4 个数 a，b，c，d 排成 2 行、2 列，两边各加一条竖直线记成 ab cd ， 概念 =ad-bc，上述记号就叫做 2 阶行列式．若 11 11 xx xx  =8，则 x= ． 思路分析：根据题中的新概念将所求的方程化为普通方程，整理后即可求出方程的解，即为 x 的值． 解：根据题意化简 =8，得：（x+1）2-（1-x）2=8， 2 整理得：x2+2x+1-（1-2x+x2）-8=0，即 4x=8， 解得：x=2． 故答案为：2 点评：此题考查了整式的混合运算，属于新概念的题型，涉及的知识有：完全平方公式，去 括号、合并同类项法则，根据题意将所求的方程化为普通方程是解本题的关键． 对应训练 2．（ 2012•株洲）若（x1，y1）•（x2，y2）=x1x2+y1y2，则（4，5）•（6，8）= ． 考点三：探索题型中的新概念 例 3 （2012•南京）如图，A、B 是⊙O 上的两个定点，P 是⊙O 上的动点（P 不与 A、B 重合）、我们称∠APB 是⊙O 上关于点 A、B 的滑动角． （1）已知∠APB 是⊙O 上关于点 A、B 的滑动角， ①若 AB 是⊙O 的直径，则∠APB= °； ②若⊙O 的半径是 1，AB= ，求∠APB 的度数； （2）已知 O2 是⊙O1 外一点，以 O2 为圆心作一个圆与⊙O1 相交于 A、B 两点，∠APB 是 ⊙O1 上关于点 A、B 的滑动角，直线 PA、PB 分别交⊙O2 于 M、N（点 M 与点 A、点 N 与 点 B 均不重合），连接 AN，试探索∠APB 与∠MAN、∠ANB 之间的数量关系． 思路分析：（1）①根据直径所对的圆周角等于 90°即可求解； ②根据勾股定理的逆定理可得∠AOB=90°，再分点 P 在优弧 上；点 P 在劣弧 上两种情 况讨论求解； （2）根据点 P 在⊙O1 上的位置分为四种情况得到∠APB 与∠MAN、∠ANB 之间的数量关 系． 解：（1）①若 AB 是⊙O 的直径，则∠APB=90． ②如图，连接 AB、OA、OB． 在△ AOB 中， ∵OA=OB=1．AB= ， ∴OA2+OB2=AB2． ∴∠AOB=90°． 当点 P 在优弧 上时，∠AP1B= ∠AOB=45°； 当点 P 在劣弧 上时，∠AP2B= （360°﹣∠AOB）=135°…6 分 （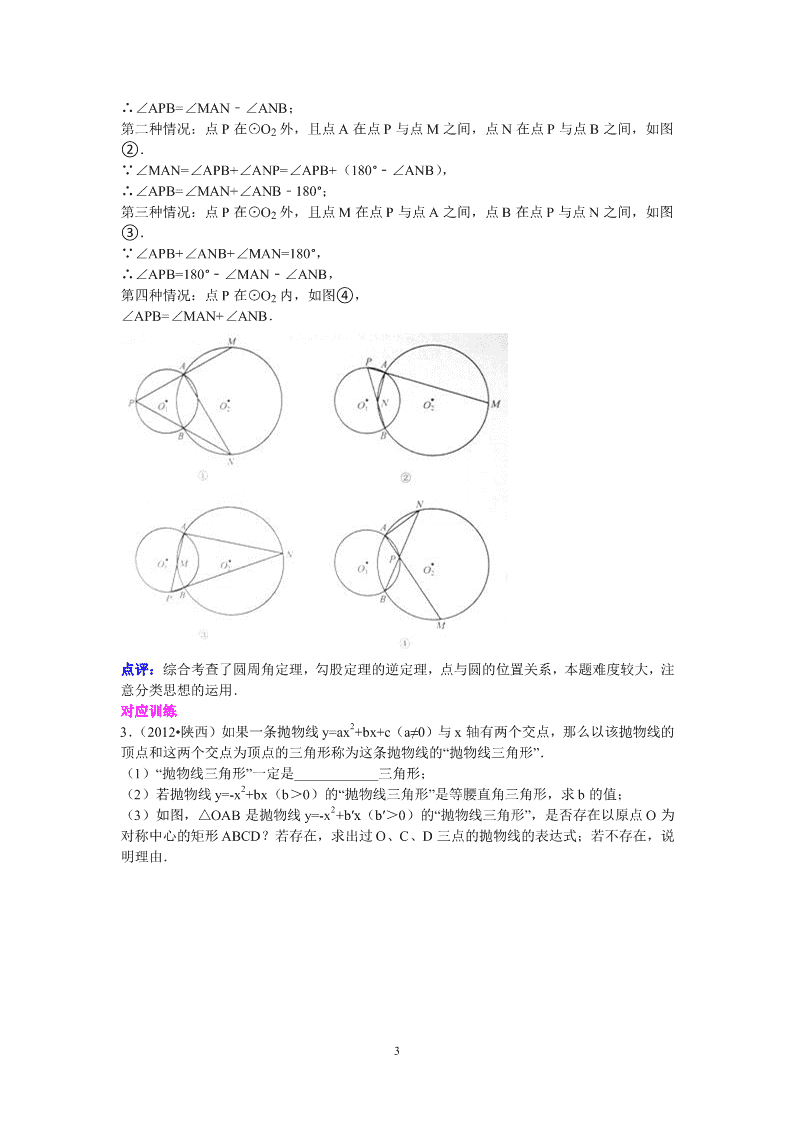2）根据点 P 在⊙O1 上的位置分为以下四种情况． 第一种情况：点 P 在⊙O2 外，且点 A 在点 P 与点 M 之间，点 B 在点 P 与点 N 之间，如图 ① ∵∠MAN=∠APB+∠ANB， 3 ∴∠APB=∠MAN﹣∠ANB； 第二种情况：点 P 在⊙O2 外，且点 A 在点 P 与点 M 之间，点 N 在点 P 与点 B 之间，如图 ②． ∵∠MAN=∠APB+∠ANP=∠APB+（180°﹣∠ANB）， ∴∠APB=∠MAN+∠ANB﹣180°； 第三种情况：点 P 在⊙O2 外，且点 M 在点 P 与点 A 之间，点 B 在点 P 与点 N 之间，如图 ③． ∵∠APB+∠ANB+∠MAN=180°， ∴∠APB=180°﹣∠MAN﹣∠ANB， 第四种情况：点 P 在⊙O2 内，如图④， ∠APB=∠MAN+∠ANB． 点评：综合考查了圆周角定理，勾股定理的逆定理，点与圆的位置关系，本题难度较大，注 意分类思想的运用． 对应训练 3．（ 2012•陕西）如果一条抛物线 y=ax2+bx+c（a≠0）与 x 轴有两个交点，那么以该抛物线的 顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”． （1）“抛物线三角形”一定是 三角形； （2）若抛物线 y=-x2+bx（b＞0）的“抛物线三角形”是等腰直角三角形，求 b 的值； （3）如图，△OAB 是抛物线 y=-x2+b′x（b′＞0）的“抛物线三角形”，是否存在以原点 O 为 对称中心的矩形 ABCD？若存在，求出过 O、C、D 三点的抛物线的表达式；若不存在，说 明理由． 4 考点四：开放题型中的新概念 例 4 （2012•北京）在平面直角坐标系 xOy 中，对于任意两点 P1（x1，y1）与 P2（x2，y2） 的“非常距离”，给出如下概念： 若|x1-x2|≥|y1-y2|，则点 P1 与点 P2 的“非常距离”为|x1-x2|； 若|x1-x2|＜|y1-y2|，则点 P1 与点 P2 的“非常距离”为|y1-y2|． 例如：点 P1（1，2），点 P2（3，5），因为|1-3|＜|2-5|，所以点 P1 与点 P2 的“非常距离”为|2-5|=3， 也就是图 1 中线段 P1Q 与线段 P2Q 长度的较大值（点 Q 为垂直于 y 轴的直线 P1Q 与垂直于 x 轴的直线 P2Q 交点）． （1）已知点 A（- 1 2 ，0）， B 为 y 轴上的一个动点， ①若点 A 与点 B 的“非常距离”为 2，写出一个满足条件的点 B 的坐标； ②直接写出点 A 与点 B 的“非常距离”的最小值； （2）已知 C 是直线 y= 3 4 x+3 上的一个动点， ①如图 2，点 D 的坐标是（0，1），求点 C 与点 D 的“非常距离”的最小值及相应的点 C 的坐 标； ②如图 3，E 是以原点 O 为圆心，1 为半径的圆上的一个动点，求点 C 与点 E 的“非常距离” 的最小值及相应的点 E 与点 C 的坐标． 思路分析：（1）①根据点 B 位于 y 轴上，可以设点 B 的坐标为（0，y）．由“非常距离”的概 念可以确定|0-y|=2，据此可以求得 y 的值； ②设点B的坐标为（0，y）．因为|- -0|≥|0-y|，所以点A与点B的“非常距离”最小值为|- -0|= ； 5 （2）①设点 C 的坐标为（x0， 3 4 x0+3）．根据材料“若|x1-x2|≥|y1-y2|，则点 P1 与点 P2 的“非常 距离”为|x1-x2|”知，C、D 两点的“非常距离”的最小值为-x0= x0+2，据此可以求得点 C 的 坐标； ②当点 E 在过原点且与直线 y= x+3 垂直的直线上时，点 C 与点 E 的“非常距离”最小，即 E（- 3 5 ， 4 5 ）．解答思路同上． 解：（1）①∵B 为 y 轴上的一个动点， ∴设点 B 的坐标为（0，y）． ∵|- 1 2 -0|= ≠2， ∴|0-y|=2， 解得，y=2 或 y=-2； ∴点 B 的坐标是（0，2）或（0，-2）； ②点 A 与点 B 的“非常距离”的最小值为 ； （2）①∵C 是直线 y= 3 4 x+3 上的一个动点， ∴设点 C 的坐标为（x0， x0+3）， ∴-x0= x0+2， 此时，x0=- 8 7 ， ∴点 C 与点 D 的“非常距离”的最小值为： ， 此时 C（- ，15 7 ）； ②E（- 3 5 ， 4 5 ）． - -x0= x0+3- 4 5 ， 6 解得，x0=- 8 5 ， 则点 C 的坐标为（- ， 9 5 ）， 最小值为 1． 点评：本题考查了一次函数综合题．对于信息给予题，一定要弄清楚题干中的已知条件．本 题中的“非常距离”的概念是正确解题的关键． 对应训练 4．（2012•台州）请你规定一种适合任意非零实数 a，b 的新运算“a⊕b”，使得下列算式成立： 1⊕2=2⊕1=3，（ -3）⊕（-4）=（-4）⊕（-3）=- 7 6 ，（ -3）⊕5=5⊕（-3）=- 4 15 ，… 你规定的新运算 a⊕b= （用 a，b 的一个代数式表示）． 考点五：阅读材料题型中的新概念 例 5 （2012•常州）平面上有两条直线 AB、CD 相交于点 O，且∠BOD=150°（如图），现 按如下要求规定此平面上点的“距离坐标”： （1）点 O 的“距离坐标”为（0，0）； （2）在直线 CD 上，且到直线 AB 的距离为 p（p＞0）的点的“距离坐标”为（p，0）；在直 线 AB 上，且到直线 CD 的距离为 q（q＞0）的点的“距离坐标”为（0，q）； （3）到直线 AB、CD 的距离分别为 p，q（p＞0，q＞0）的点的“距离坐标”为（p，q）． 设 M 为此平面上的点，其“距离坐标”为（m，n），根据上述对点的“距离坐标”的规定，解决 下列问题： （1）画出图形（保留画图痕迹）： ①满足 m=1，且 n=0 的点 M 的集合； ②满足 m=n 的点 M 的集合； （2）若点 M 在过点 O 且与直线 CD 垂直的直线 l 上，求 m 与 n 所满足的关系式．（说明： 图中 OI 长为一个单位长） 思路分析：（1）①以 O 为圆心，以 2 为半径作圆，交 CD 于两点，则此两点为所求；②分 别作∠BOC 和∠BOD 的角平分线并且反向延长，即可求出答案； （2）过 M 作 MN⊥AB 于 N，根据已知得出 OM=n，MN=m，求出∠NOM=60°，根据锐角 三角函数得出 sin60°= MN OM = m n ，求出即可． 解：（1）①如图所示： 7 点 M1 和 M2 为所求； ②如图所示： 直线 MN 和直线 EF（O 除外）为所求； （2）如图： 过 M 作 MN⊥AB 于 N， ∵M 的“距离坐标”为（m，n）， ∴OM=n，MN=m， ∵∠BOD=150°，直线 l⊥CD， ∴∠MON=150°-90°=60°， 在 Rt△MON 中，sin60°= MN OM = m n ， 即 m 与 n 所满足的关系式是：m= 3 2 n． 点评：本题考查了锐角三角函数值，角平分线性质，含 30 度角的直角三角形的应用，主要 考查学生的动手操作能力和计算能力，注意：角平分线上的点到角两边的距离相等． 对应训练 5．（ 2012•钦州）在平面直角坐标系中，对于平面内任意一点（x，y），若规定以下两种变换： ①f（x，y）=（y，x）．如 f（2，3）=（3，2）； ②g（x，y）=（-x，-y），如 g（2，3）=（-2，-3）． 按照以上变换有：f（g（2，3）） =f（-2，-3）=（-3，-2），那么 g（f（-6，7））等于（ ） A．（ 7，6） B．（ 7，-6） C．（ -7，6） D．（ -7，-6） 四、中考真题演练 一、选择题 8 1．（ 2012•六盘水）概念：f（a，b）=（b，a）， g（m，n）=（-m，-n）．例如 f（2，3）=（3， 2）， g（-1，-4）=（1，4）．则 g[f（-5，6）]等于（ ） A．（ -6，5） B．（ -5，-6） C．（ 6，-5） D．（ -5，6） 2． （2012•湘潭）文文设计了一个关于实数运算的程序，按此程序，输入一个数后，输出 的数比输入的数的平方小 1，若输入 7 ，则输出的结果为（ ） A．5 B．6 C．7 D．8 点评：本题考查的是实数的运算，根据题意得出输出数的式子是解答此题的关键． 3． （2012•丽水）小明用棋子摆放图形来研究数的规律．图 1 中棋子围城三角形，其棵数 3，6，9，12，…称为三角形数．类似地，图 2 中的 4，8，12，16，…称为正方形数．下列 数中既是三角形数又是正方形数的是（ ） A．2010 B．2012 C．2014 D．2016 二、填空题 4．（ 2012•常德）规定用符号[m]表示一个实数 m 的整数部分，例如：[ ]=0，[3.14]=3．按 此规定[ ]的值为 ． 5．（ 2012•随州）概念：平面内的直线 1l 与 2l 相交于点 O，对于该平面内任意一点 M，点 M 到直线 、 的距离分别为 a、b，则称有序非实数对（a，b）是点 M 的“距离坐标”，根据 上述概念，距离坐标为（2，3）的点的个数是（ ） A．2 B．1 C．4 D．3 6．（ 2012•荆门）新概念：[a，b]为一次函数 y=ax+b（a≠0，a，b 为实数）的“关联数”．若“关 联数”[1，m-2]的一次函数是正比例函数，则关于 x 的方程 1 1x  + 1 m =1 的解为 ． 7．（ 2012•自贡）如图，△ABC 是正三角形，曲线 CDEF 叫做正三角形的渐开线，其中弧 CD、弧 DE、弧 EF 的圆心依次是 A、B、C，如果 AB=1，那么曲线 CDEF 的长是 ． 8． （2012•泉州）在△ABC 中，P 是 AB 上的动点（P 异于 A、B），过点 P 的直线截△ABC， 使截得的三角形与△ABC 相似，我们不妨称这种直线为过点 P 的△ABC 的相似线，简记为 P（lx）（ x 为自然数）． （1）如图①，∠A=90°，∠B=∠C，当 BP=2PA 时，P（l1）、 P（l2）都是过点 P 的△ABC 的相似线（其中 l1⊥BC，l2∥AC），此外，还有 条； 9 （2）如图②，∠C=90°，∠B=30°，当 BP BA = 时，P（lx）截得的三角形面积 为△ABC 面积的 1 4 ． 三、解答题 9．（ 2012•铜仁地区）如图，概念：在直角三角形 ABC 中，锐角 α 的邻边与对边的比叫做角 α 的余切，记作 ctanα，即 ctanα=   角 的邻边 角 的对边 = AC BC ，根据上述角的余切概念，解下列问 题： （1）ctan30°= ； （2）如图，已知 tanA= 3 4 ，其中∠A 为锐角，试求 ctanA 的值． 10．（ 2012•无锡）对于平面直角坐标系中的任意两点 P1（x1，y1），P2（x2，y2），我们把|x1-x2|+|y1-y2| 叫做 P1、P2 两点间的直角距离，记作 d（P1，P2）． （1）已知 O 为坐标原点，动点 P（x，y）满足 d（O，P）=1，请写出 x 与 y 之间满足的关 系式，并在所给的直角坐标系中画出所有符合条件的点 P 所组成的图形； （2）设 P0（x0，y0）是一定点，Q（x，y）是直线 y=ax+b 上的动点，我们把 d（P0，Q）的 最小值叫做 P0 到直线 y=ax+b 的直角距离．试求点 M（2，1）到直线 y=x+2 的直角距离． 11．（2012•厦门）如图，在平面直角坐标系中，已知点 A（2，3）、 B（6，3），连接 AB．如 果点 P 在直线 y=x-1 上，且点 P 到直线 AB 的距离小于 1，那么称点 P 是线段 AB 的“临近点”． （1）判断点 C（ 75,22 ）是否是线段 AB 的“临近点”，并说明理由； 10 （2）若点 Q（m，n）是线段 AB 的“临近点”，求 m 的取值范围． 12．（ 2012•兰州）如图，概念：若双曲线 y= k x （k＞0）与它的其中一条对称轴 y=x 相交于 A、B 两点，则线段 AB 的长度为双曲线 y= （k＞0）的对径． （1）求双曲线 y= 1 x 的对径． （2）若双曲线 y= （k＞0）的对径是 10 2 ，求 k 的值． （3）仿照上述概念，概念双曲线 y= （k＜0）的对径． 13．（ 2012•绍兴）联想三角形外心的概念，我们可引入如下概念． 概念：到三角形的两个顶点距离相等的点，叫做此三角形的准外心． 举例：如图 1，若 PA=PB，则点 P 为△ABC 的准外心． 应用：如图 2，CD 为等边三角形 ABC 的高，准外心 P 在高 CD 上，且 PD= 1 2 AB，求 ∠APB 的度数． 探究：已知△ABC 为直角三角形，斜边 BC=5，AB=3，准外心 P 在 AC 边上，试探究 PA 的长． 11 14．（ 2012•嘉兴）将△ABC 绕点 A 按逆时针方向旋转 θ 度，并使各边长变为原来的 n 倍， 得△AB′C′，即如图①，我们将这种变换记为[θ，n]． （1）如图①，对△ABC 作变换[60°， 3 ]得△AB′C′，则 S△AB′C′：S△ABC= ；直线 BC 与直线 B′C′所夹的锐角为 度； （2）如图②，△ABC 中，∠BAC=30°，∠ACB=90°，对△ABC 作变换[θ，n]得△AB'C'， 使点 B、C、C′在同一直线上，且四边形 ABB'C'为矩形，求 θ 和 n 的值； （3）如图③，△ABC 中，AB=AC，∠BAC=36°，BC=l，对△ABC 作变换[θ，n]得△AB′C′， 使点 B、C、B′在同一直线上，且四边形 ABB'C'为平行四边形，求 θ 和 n 的值． 15．（ 2012•台州）概念：P、Q 分别是两条线段 a 和 b 上任意一点，线段 PQ 长度的最小值 叫做线段 a 与线段 b 的距离． 已知 O（0，0）， A（4，0）， B（m，n）， C（m+4，n）是平面直角坐标系中四点． （1）根据上述概念，当 m=2，n=2 时，如图 1，线段 BC 与线段 OA 的距离是 ； 当 m=5，n=2 时，如图 2，线段 BC 与线段 OA 的距离（即线段 AB 长）为 ； （2）如图 3，若点 B 落在圆心为 A，半径为 2 的圆上，线段 BC 与线段 OA 的距离记为 d， 求 d 关于 m 的函数解析式． （3）当 m 的值变化时，动线段 BC 与线段 OA 的距离始终为 2，线段 BC 的中点为 M， ①求出点 M 随线段 BC 运动所围成的封闭图形的周长； ②点 D 的坐标为（0，2）， m≥0，n≥0，作 MN⊥x 轴，垂足为 H，是否存在 m 的值使以 A、 M、H 为顶点的三角形与△AOD 相似？若存在，求出 m 的值；若不存在，请说明理由． 12 专题讲座二：新概念型问题参考答案 三、中考典例剖析 对应训练 1． 3 4 解：∵x1=- 1 3 ， ∴x2= 1 11 ( )3 = ，x3= 1 31 ( )4 =4，x4= 11 1 4 3 ， ∴差倒数为 3 个循环的数， ∵2012=670×3+2， ∴x2012=x2= ， 故答案为： ． 2．64 解：∵（x1，y1）•（x2，y2）=x1x2+y1y2， ∴（4，5）•（6，8）=4×6+5×8=64， 故答案为 64． 3．解：（1）如图； 根据抛物线的对称性，抛物线的顶点 A 必在 O、B 的垂直平分线上，所以 OA=AB，即：“抛 物线三角形”必为等腰三角形． 故填：等腰． （2）∵抛物线 y=-x2+bx（b＞0）的“抛物线三角形”是等腰直角三角形， ∴该抛物线的顶点（ 2 ,24 bb）满足 2 24 bb （b＞0）． ∴b=2． 13 （3）存在． 如图，作△OCD 与△OAB 关于原点 O 中心对称，则四边形 ABCD 为平行四边形． 当 OA=OB 时，平行四边形 ABCD 是矩形， 又∵AO=AB， ∴△OAB 为等边三角形． 作 AE⊥OB，垂足为 E， ∴AE= 3 OE． ∴ 2 4 b = 3 • 2 b （b′＞0）． ∴b′=2 ． ∴A（ ，3）， B（2 ，0）． ∴C（- ，-3）， D（-2 ，0）． 设过点 O、C、D 的抛物线为 y=mx2+nx，则 12 2 3 0 3 3 3 mn mn      ， 解得 1 23 m n   ． 故所求抛物线的表达式为 y=x2+2 3 x． 4．解：根据题意可得： 1⊕2=2⊕1=3= 22 12 ， （-3）⊕（-4）=（-4）⊕（-3）=- 7 6 = 22 34 ， （-3）⊕5=5⊕（-3）=- 4 15 = 22 35 ， 14 则 a⊕b= 22 ab = 22ab ab  ． 故答案为： ． 5．C 解：∵f（-6，7）=（7，-6）， ∴g（f（-6，7）） =g（7，-6）=（-7，6）． 故选 C． 四、中考真题演练 一、选择题 1．A 2．B． 3．D 解：∵3，6，9，12，…称为三角形数， ∴三角数都是 3 的倍数， ∵4，8，12，16，…称为正方形数， ∴正方形数都是 4 的倍数， ∴既是三角形数又是正方形数的是 12 的倍数， ∵2010÷12=167…6， 2012÷12=167…8， 2014÷12=167…10， 2016÷12=168， ∴2016 既是三角形数又是正方形数． 故选 D． 二、填空题 4．4 解：∵3＜ ＜4， ∴3+1＜ +1＜4+1， ∴4＜ +1＜5， ∴[ +1]=4， 故答案为：4． 5．C 解：如图所示，所求的点有 4 个， 15 故选 C． 6．x=3 解：根据题意可得：y=x+m-2， ∵“关联数”[1，m-2]的一次函数是正比例函数， ∴m-2=0， 解得：m=2， 则关于 x 的方程 1 1x  + 1 m =1 变为 + 1 2 =1， 解得：x=3， 检验：把 x=3 代入最简公分母 2（x-1）=4≠0， 故 x=3 是原分式方程的解， 故答案为：x=3． 7．4π 解：弧 CD 的长是120 1 180   = 2 3  ， 弧 DE 的长是：120 2 180   = 4 3  ， 弧 EF 的长是：120 3 180   =2π， 则曲线 CDEF 的长是： + +2π=4π． 故答案是：4π． 8．（1）1；（ 2） 1 2 或 3 4 或 3 4 解：（1）存在另外 1 条相似线． 如图 1 所示，过点 P 作 l3∥BC 交 AC 于 Q，则△APQ∽△ABC； 故答案为：1； （2）设 P（lx）截得的三角形面积为 S，S= 1 4 S△ABC，则相似比为 1：2． 如图 2 所示，共有 4 条相似线： 16 ①第 1 条 l1，此时 P 为斜边 AB 中点，l1∥AC，∴ BP BA = 1 2 ； ②第 2 条 l2，此时 P 为斜边 AB 中点，l2∥AC，∴ = ； ③第 3 条 l3，此时 BP 与 BC 为对应边，且 BP BC = ，∴ = cos30BP BC = 3 4 ； ④第 4 条 l4，此时 AP 与 AC 为对应边，且 AP AC = ，∴ 1sin30 4 AP AP AB AC， ∴ = 3 4 ． 故答案为： 1 2 或 3 4 或 3 4 ． 三、解答题 9．解：（1）∵Rt△ABC 中，α=30°， ∴BC= 1 2 AB， ∴AC= 22AB BC = 221 4AB AB = 3 2 AB， ∴ctan30°= AC BC = 3 ． 故答案为： ； （2）∵tanA= 3 4 ， ∴设 BC=3，AC=4，则 AB=5， ∴ctanA= = 4 3 ． 10．解：（1）由题意，得|x|+|y|=1， 所有符合条件的点 P 组成的图形如图所示。 17 （2）∵d（M，Q）=|x-2|+|y-1|=|x-2|+|x+2-1|=|x-2|+|x+1|， 又∵x 可取一切实数，|x-2|+|x+1|表示数轴上实数 x 所对应的点到数 2 和-1 所对应的点的距 离之和，其最小值为 3． ∴点 M（2，1）到直线 y=x+2 的直角距离为 3。 11．解：（1）点 C（ 75,22 ）是线段 AB 的“临近点”．理由是： ∵点 P 到直线 AB 的距离小于 1，A、B 的纵坐标都是 3， ∴AB∥x 轴，3-1=2，3+1=4， ∴当纵坐标 y 在 2＜y＜4 范围内时，点是线段 AB 的“临近点”，点 C 的坐标是（ ）， ∴y= 5 2 ＞2，且小于 4， ∵C（ ）在直线 y=x-1 上， ∴点 C（ ）是线段 AB 的“临近点”． （2）由（1）知：线段 AB 的“临近点”的纵坐标的范围是 2＜y＜4， 把 y=2 代入 y=x-1 得：x=3， 把 y=4 代入 y=x-1 得：x=5， ∴3＜x＜5， ∵点 Q（m，n）是线段 AB 的“临近点”， ∴m 的取值范围是 3＜m＜5． 12．解：过 A 点作 AC⊥x 轴于 C，如图， 18 （1）解方程组 1y x yx     ，得 1 1 1 1 x y    ， 2 2 1 1 x y    ， ∴A 点坐标为（1，1）， B 点坐标为（-1，-1）， ∴OC=AC=1， ∴OA= 2 OC= ， ∴AB=2OA=2 ， ∴双曲线 y= 1 x 的对径是 2 ； （2）∵双曲线的对径为 10 ，即 AB=10 ，OA=5 ， ∴OA= OC= AC， ∴OC=AC=5， ∴点 A 坐标为（5，5）， 把 A（5，5）代入双曲线 y= k x （k＞0）得 k=5×5=25， 即 k 的值为 25； （3）若双曲线 y= （k＜0）与它的其中一条对称轴 y=-x 相交于 A、B 两点， 则线段 AB 的长称为双曲线 y= （k＜0）的对径． 13．解：①若 PB=PC，连接 PB，则∠PCB=∠PBC， ∵CD 为等边三角形的高， ∴AD=BD，∠PCB=30°， ∴∠PBD=∠PBC=30°， ∴PD= 3 3 DB= 3 6 AB， 19 与已知 PD= 1 2 AB 矛盾，∴PB≠PC， ②若 PA=PC，连接 PA，同理可得 PA≠PC， ③若 PA=PB，由 PD= AB，得 PD=BD， ∴∠APD=45°， 故∠APB=90°； 探究：解：∵BC=5，AB=3， ∴AC= 22BC AB = 2253 =4， ①若 PB=PC，设 PA=x，则 x2+32=（4-x）2， ∴x= 7 8 ，即 PA= ， ②若 PA=PC，则 PA=2， ③若 PA=PB，由图知，在 Rt△PAB 中，不可能． 故 PA=2 或 ． 14．解：（1）根据题意得：△ABC∽△AB′C′， ∴S△AB′C′：S△ABC=（ AB AB ）2=（ 3 ）2=3，∠B=∠B′， ∵∠ANB=∠B′NM， ∴∠BMB′=∠BAB′=60°； 故答案为：3，60； （2）∵四边形 ABB′C′是矩形， ∴∠BAC′=90°． ∴θ=∠CAC′=∠BAC′-∠BAC=90°-30°=60°． 在 Rt△ABC 中，∠ABB'=90°，∠BAB′=60°， ∴∠AB′B=30°， ∴n= AB AB  =2； （3）∵四边形 ABB′C′是平行四边形， 20 ∴AC′∥BB′， 又∵∠BAC=36°， ∴θ=∠CAC′=∠ACB=72°． ∴∠BB′A=∠BAC=36°，而∠B=∠B， ∴△ABC∽△B′BA， ∴AB：BB′=CB：AB， ∴AB2=CB•BB′=CB（BC+CB′）， 而 CB′=AC=AB=B′C′，BC=1， ∴AB2=1（1+AB）， ∴AB= 51 2 ， ∵AB＞0， ∴n= BC BC = 51 2 ． 15．解：（1）当 m=2，n=2 时， 如题图 1，线段 BC 与线段 OA 的距离等于平行线之间的距离，即为 2； 当 m=5，n=2 时， B 点坐标为（5，2），线段 BC 与线段 OA 的距离，即为线段 AB 的长， 如答图 1，过点 B 作 BN⊥x 轴于点 N，则 AN=1，BN=2， 在 Rt△ABN 中，由勾股定理得：AB= 2 2 2 212AN BN   = 5 ． （2）如答图 2 所示，当点 B 落在⊙A 上时，m 的取值范围为 2≤m≤6： 当 4≤m≤6，显然线段 BC 与线段 OA 的距离等于⊙A 半径，即 d=2； 当 2≤m＜4 时，作 BN⊥x 轴于点 N，线段 BC 与线段 OA 的距离等于 BN 长， ON=m，AN=OA-ON=4-m，在 Rt△ABN 中，由勾股定理得： ∴d= 222 (4 )m = 4 16 8mm   = 2 8 12mm   ． 21 （3）①依题意画出图形，点 M 的运动轨迹如答图 3 中粗体实线所示： 由图可见，封闭图形由上下两段长度为 8 的线段，以及左右两侧半径为 2 的半圆所组成， 其周长为：2×8+2×π×2=16+4π， ∴点 M 随线段 BC 运动所围成的封闭图形的周长为：16+4π． ②结论：存在． ∵m≥0，n≥0，∴点 M 位于第一象限． ∵A（4，0）， D（0，2）， ∴OA=2OD． 如图 4 所示，相似三角形有三种情形： （I）△AM1H1，此时点 M 纵坐标为 2，点 H 在 A 点左侧． 如图，OH1=m+2，M1H1=2，AH1=OA-OH1=2-m， 由相似关系可知，M1H1=2AH1，即 2=2（2-m）， ∴m=1； （II）△AM2H2，此时点 M 纵坐标为 2，点 H 在 A 点右侧． 如图，OH2=m+2，M2H2=2，AH2=OH2-OA=m-2， 22 由相似关系可知，M2H2=2AH2，即 2=2（m-2）， ∴m=3； （III）△AM3H3，此时点 B 落在⊙A 上． 如图，OH3=m+2，AH3=OH3-OA=m-2， 过点 B 作 BN⊥x 轴于点 N，则 BN=M3H3=n，AN=m-4， 由相似关系可知，AH3=2M3H3，即 m-2=2n （1） 在 Rt△ABN 中，由勾股定理得：22=（m-4）2+n2 （2） 由（1）、（2）式解得：m1= 26 5 ，m2=2， 当 m=2 时，点 M 与点 A 横坐标相同，点 H 与点 A 重合，故舍去， ∴m= ． 综上所述，存在 m 的值使以 A、M、H 为顶点的三角形与△AOD 相似，m 的取值为：1、3 或 ．