2008年数学中考试题分类汇编（实验与操作专题） 12页

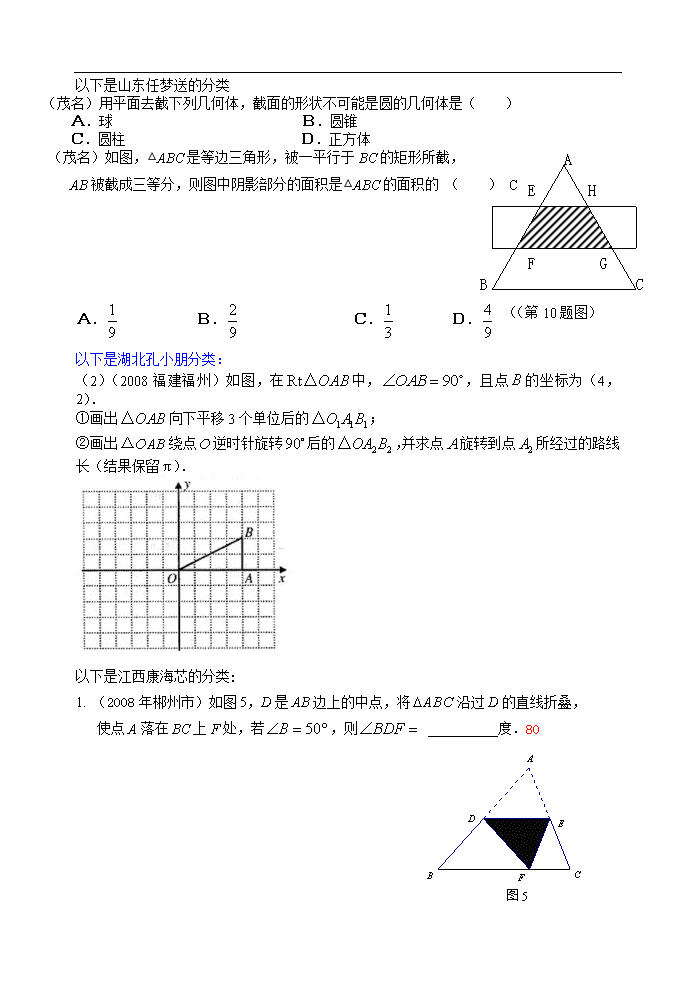
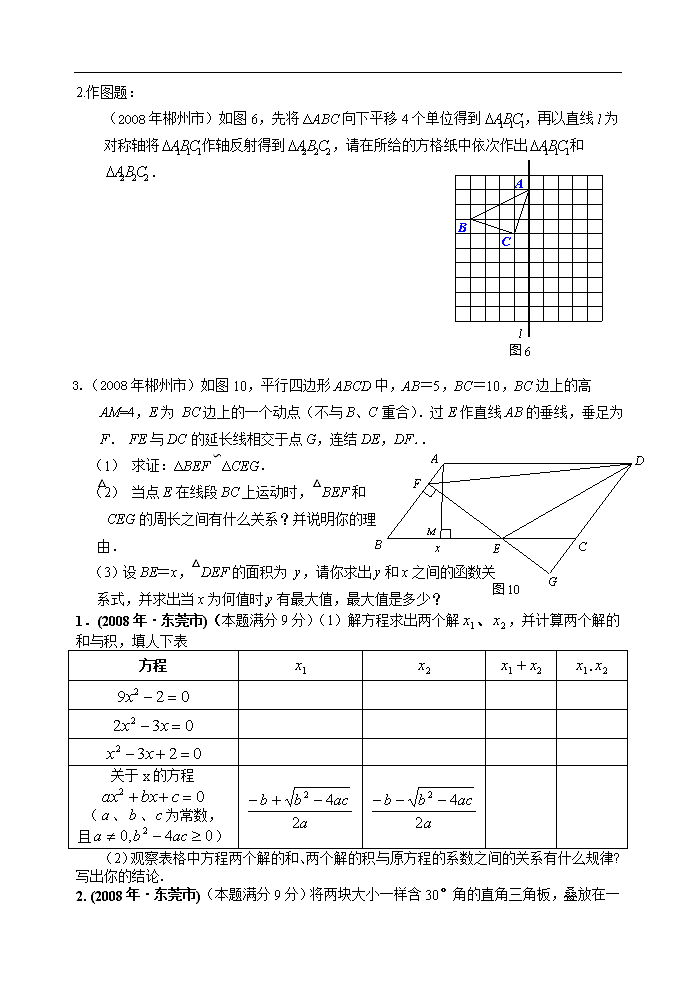
以下是山东任梦送的分类 ‎（茂名）用平面去截下列几何体，截面的形状不可能是圆的几何体是（ ）‎ ‎ Ａ．球 Ｂ．圆锥 ‎ E H F G C B A ‎（（第10题图）‎ ‎ Ｃ．圆柱 Ｄ．正方体 ‎（茂名）如图，△ABC是等边三角形，被一平行于BC的矩形所截，‎ AB被截成三等分，则图中阴影部分的面积是△ABC的面积的 （ ） C ‎ Ａ． Ｂ． Ｃ． Ｄ．‎ 以下是湖北孔小朋分类：‎ ‎（2）（2008福建福州）如图，在中，，且点的坐标为（4，2）．‎ ‎①画出向下平移3个单位后的；‎ ‎②画出绕点逆时针旋转后的，并求点旋转到点所经过的路线长（结果保留）．‎ 以下是江西康海芯的分类:‎ ‎1. （2008年郴州市）如图5，D是AB边上的中点，将沿过D的直线折叠，‎ 使点A落在BC上F处，若，则 __________度．80‎ 图5‎ ‎2.作图题：‎ ‎（2008年郴州市）图6‎ 如图6，先将ΔABC向下平移4个单位得到，再以直线l为对称轴将作轴反射得到，请在所给的方格纸中依次作出和．‎ 图10‎ ‎3.（2008年郴州市）如图10，平行四边形ABCD中，AB＝5，BC＝10，BC边上的高AM=4，E为 BC边上的一个动点（不与B、C重合）．过E作直线AB的垂线，垂足为F． FE与DC的延长线相交于点G，连结DE，DF．．‎ ‎（1） 求证：ΔBEF ∽ΔCEG．‎ ‎（2） 当点E在线段BC上运动时，△BEF和△CEG的周长之间有什么关系？并说明你的理由．‎ ‎（3）设BE＝x，△DEF的面积为 y，请你求出y和x之间的函数关系式，并求出当x为何值时,y有最大值，最大值是多少？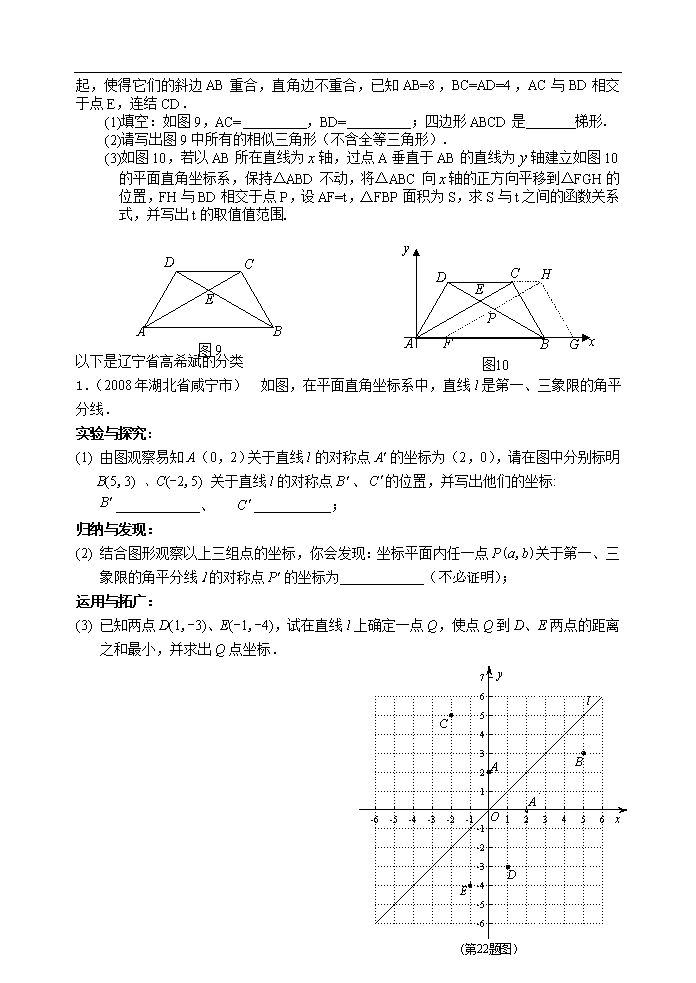 ‎ ‎1．(2008年·东莞市)（本题满分9分）（1）解方程求出两个解、，并计算两个解的和与积，填人下表 方程 ‎.‎ 关于x的方程 ‎（、、为常数，‎ 且）‎ ‎（2）观察表格中方程两个解的和、两个解的积与原方程的系数之间的关系有什么规律?写出你的结论.‎ ‎2. (2008年·东莞市)（本题满分9分）将两块大小一样含30°‎ 角的直角三角板，叠放在一起，使得它们的斜边AB重合，直角边不重合，已知AB=8，BC=AD=4，AC与BD相交于点E，连结CD．‎ ‎(1)填空：如图9，AC= ，BD= ；四边形ABCD是 梯形.‎ ‎(2)请写出图9中所有的相似三角形（不含全等三角形）.‎ ‎(3)如图10，若以AB所在直线为轴，过点A垂直于AB的直线为轴建立如图10的平面直角坐标系，保持ΔABD不动，将ΔABC向轴的正方向平移到ΔFGH的位置，FH与BD相交于点P，设AF=t，ΔFBP面积为S，求S与t之间的函数关系式，并写出t的取值值范围.‎ E D C H F G B A P y x 图10‎ ‎10‎ D C B A E 图9‎ 以下是辽宁省高希斌的分类 ‎1．（2008年湖北省咸宁市） 如图，在平面直角坐标系中，直线l是第一、三象限的角平分线．‎ 实验与探究：‎ (1) 由图观察易知A（0，2）关于直线l的对称点的坐标为（2，0），请在图中分别标明 B(5,3) 、C(-2,5) 关于直线l的对称点、的位置，并写出他们的坐标: ‎ ‎ 、 ；‎ 归纳与发现：‎ (2) 结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点的坐标为 （不必证明）；‎ 运用与拓广：‎ (3) 已知两点D(1,-3)、E(-1,-4)，试在直线l上确定一点Q，使点Q到D、E两点的距离之和最小，并求出Q点坐标．‎ ‎2．（2008年湖北省荆州市）如图，等腰直角三角形纸片ABC中，AC＝BC＝4，∠ACB＝90º，直角边AC在x轴上，B点在第二象限，A（1，0），AB交y轴于E，将纸片过E点折叠使BE与EA所在直线重合，得到折痕EF（F在x轴上），再展开还原沿EF剪开得到四边形BCFE，然后把四边形BCFE从E点开始沿射线EA平移，至B点到达A点停止.设平移时间为t（s），移动速度为每秒1个单位长度，平移中四边形BCFE与△AEF重叠的面积为S.‎ ‎ （1）求折痕EF的长；‎ ‎ （2）是否存在某一时刻t使平移中直角顶点C经过抛物线的顶点？若存在，求出t值；若不存在，请说明理由；‎ O C x A C1‎ F1‎ E1‎ B1‎ B F E y ‎ （3）直接写出S与t的函数关系式及自变量t的取值范围.‎ ‎ ‎ ‎3．（2008年湖北省鞥仙桃市潜江市江汉油田）小华将一张矩形纸片（如图1）沿对角线剪开，得到两张三角形纸片（如图2），其中，然后将这两张三角形纸片按如图3所示的位置摆放，纸片的直角顶点落在纸片的斜边上，直角边落在所在的直线上.‎ （1） 若与相交于点，取的中点，连接、，当纸片沿方向平移时（如图3），请你观察、测量、的长度，猜想并写出与的数量关系，然后证明你的猜想；‎ （2） 在（1）的条件下，求出的大小（用含的式子表示），并说明当°时， 是什么三角形？‎ （3） 在图3的基础上，将纸片绕点逆时针旋转一定的角度（旋转角度小于90°），此时变成，同样取的中点，连接、（如图4），请继续探究与的数量关系和的大小，直接写出你的猜想，不需要证明，并说明为何值时，为等边三角形.‎ 图1‎ 图2‎ 图4‎ 图3‎ ‎ ‎ ．（2008年龙岩市）（12分）如图，在平面直角坐标系中，将四边形ABCD称为“基本图形”，且各点的坐标分别为A（4，4），B（1，3），C（3，3），D（3，1）.‎ ‎（1）画出“基本图形”关于原点O对称的四边形A1B‎1C1D1，并求出A1，B1，C1，D1的坐标.‎ A1( ， )，B1( ， )，C1( ， )，D1( ， ) ；‎ ‎（2）画出“基本图形”关于x轴的对称图形A2B‎2C2D2 ；‎ ‎（3）画出四边形A3B‎3C3D3，使之与前面三个图形组成的图形既是中心对称图形又是轴对称图形.‎ ‎（第22题图）‎ ‎20（2008乌鲁木齐）．如图7，河流两岸互相平行，是河岸上间隔‎50m的两个电线杆．某人在河岸上的处测得，然后沿河岸走了‎100m到达处，测得，求河流的宽度的值（结果精确到个位）．‎ B E D C F a b A 图7‎ ‎． ‎ ‎21．(2008年宁波市)（1）如图1，中，，请用直尺和圆规作一条直线，把分割成两个等腰三角形（不写作法，但须保留作图痕迹）．‎ ‎（2）已知内角度数的两个三角形如图2、图3所示．请你判断，能否分别画一条直线把它们分割成两个等腰三角形？若能，请写出分割成的两个等腰三角形顶角的度数．‎ ‎（第21题）‎ A B C 图1‎ A B C 图2‎ ‎24°‎ ‎24°‎ ‎84°‎ A B C 图3‎ ‎104°‎ ‎52°‎ ‎①标准纸“2开”纸、“4开”纸、“8开”纸、“16开”纸……都是矩形．‎ ‎②本题中所求边长或面积都用含的代数式表示．‎ ‎26．(2008年宁波市)如图1，把一张标准纸一次又一次对开，得到“2开”纸、“4开”纸、“8开”纸、“16开”纸…．已知标准纸的短边长为．‎ ‎（1）如图2，把这张标准纸对开得到的“16开”张纸按如下步骤折叠：‎ 第一步 将矩形的短边与长边对齐折叠，点落在上的点处，铺平后得折痕；‎ 第二步 将长边与折痕对齐折叠，点正好与点重合，铺平后得折痕．‎ 则的值是 ，的长分别是 ， ．‎ ‎（2）“2开”纸、“4开”纸、“8开”纸的长与宽之比是否都相等？若相等，直接写出这个比值；若不相等，请分别计算它们的比值．‎ ‎（3）如图3，由8个大小相等的小正方形构成“”型图案，它的四个顶点分别在“16开”纸的边上，求的长．‎ A B C D B C A D E G H F F E ‎4开 ‎2开 ‎8开 ‎16开 图1‎ 图2‎ 图3‎ ‎（第26题）‎ a ‎（4）已知梯形中，，，，且四个顶点都在“4开”纸的边上，请直接写出2个符合条件且大小不同的直角梯形的面积．‎ ‎(2008年西宁市) 27．某校九年级（2）班在测量校内旗杆高度的数学活动中，第一组的同学设计了两种测量方案，并根据测量结果填写了如下《数学活动报告》中的一部分．‎ 数学活动报告 活动小组：第一组 活动地点：学校操场 活动时间：××××年××月××日年上午9：00 活动小组组长：×××‎ 课题 测量校内旗杆高度 目的 运用所学数学知识及数学方法解决实际问题——测量旗杆高度 方案 B A C D M N 方案一 方案二 方案三 示意图 D A M C N G B 测量工具 皮尺、测角仪 皮尺、测角仪 测量数据：‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ 计算过程（结 果保留根号）‎ 解：‎ 解：‎ 测量结果 ‎2.(2008年益阳) (本题10分)‎ 两个全等的直角三角形ABC和DEF重叠在一起，其中∠A=60°，AC=1. 固定△ABC不动，将△DEF进行如下操作：‎ ‎ (1) 如图11(1)，△DEF沿线段AB向右平移(即D点在线段AB内移动)，连结DC、CF、FB，四边形CDBF的形状在不断的变化，但它的面积不变化，请求出其面积.‎ A B E F C D 图11(1)‎ 温馨提示：由平移性质可得CF∥AD，CF=AD ‎(2)如图11(2)，当D点移到AB的中点时，请你猜想四边形CDBF的形状，并说明理由.‎ A B E F C D 图11(2)‎ ‎(3)如图11(3)，△DEF的D点固定在AB的中点，然后绕D点按顺时针方向旋转△DEF，使DF落在AB边上，此时F点恰好与B点重合，连结AE，请你求出sinα的值.‎ A B ‎(E)‎ ‎(F)‎ C D 图11(3)‎ E ‎(F)‎ α ‎20（2008乌鲁木齐）．如图7，河流两岸互相平行，是河岸上间隔‎50m的两个电线杆．某人在河岸上的处测得，然后沿河岸走了‎100m到达处，测得，求河流的宽度的值（结果精确到个位）．‎ B E D C F a b A 图7‎ ‎．解：过点作，交于 ‎， 2分 四边形是平行四边形 4分 m，m， 6分 又，故，m 8分 在中，m 11分 答：河流的宽度的值为‎43m． 12分 ‎(08河南)‎ ‎18．（9分）复习“全等三角形”的知识时，老师布置了一道作业题：“如图①，已知在△ABC中，AB=AC，P是△ABC内部任意一点，将AP绕A顺时针旋转至AQ，使∠QAP=∠BAC，连接 BQ、CP，则BQ=CP．”‎ 小亮是个爱动脑筋的同学，他通过对图①的分析，证明了△ABQ≌△ACP，从而证得BQ=CP之后，将点P移到等腰三角形ABC之外，原题中的条件不变，发现“BQ=CP”仍然成立，请你就图②给出证明．‎ 图①‎ 图②‎ 以下是安徽省马鞍山市成功中学的汪宗兴老师的分类 ‎20．(2008年·东莞市)（本题满分9分）（1）解方程求出两个解、，并计算两个解的和与积，填人下表 方程 ‎.‎ 关于x的方程 ‎（、、为常数，‎ 且）‎ ‎（2）观察表格中方程两个解的和、两个解的积与原方程的系数之间的关系有什么规律?写出你的结论.‎ ‎22. (2008年·东莞市)（本题满分9分）将两块大小一样含30°角的直角三角板，叠放在一起，使得它们的斜边AB重合，直角边不重合，已知AB=8，BC=AD=4，AC与BD相交于点E，连结CD．‎ ‎(1)填空：如图9，AC= ，BD= ；四边形ABCD是 梯形.‎ ‎(2)请写出图9中所有的相似三角形（不含全等三角形）.‎ ‎(3)如图10，若以AB所在直线为轴，过点A垂直于AB的直线为轴建立如图10的平面直角坐标系，保持ΔABD不动，将ΔABC向轴的正方向平移到ΔFGH的位置，FH与BD相交于点P，设AF=t，ΔFBP面积为S，求S与t之间的函数关系式，并写出t的取值值范围.‎ E D C H F G B A P y x 图10‎ ‎10‎ D C B A E 图9‎ ‎1.（2008年聊城市）把一张正方形纸片按如图所示的方法对折两次后剪去两个角，那么打开以后的形状是（ ）‎ 第9题图 ‎2.（2008年聊城市）随地震波而来的是地底积蓄已久的能量．因为里氏震级并不像摄氏温度一样是等分性的指标，因此每两级地震所释放的能量也相差巨大．根据里克特在1953年提出的公式计算，每一级地震释放的能量都是次一级地震的倍．这意味着，里氏震级每高出0.1级，就会多释放出0.4125倍的能量（如7.8级比7.7级会多释放出0.4125倍的能量）．那么‎5月12日下午2时28分四川汶川地区发生的8.0级大地震与‎5月25日下午4时21分四川青川一带发生的6.4级余震相比，前次所释放的能量约是后次的（ ）‎ A．22倍 B．34倍 C．40倍 D．251倍 ‎1、（2008年宜宾市）将直角边长为‎5cm的等腰直角ΔABC绕点A逆时针旋转15°后,得到ΔAB’C’,则图中阴影部分的面积是 cm2‎ ‎21．(2008年宁波市)（1）如图1，中，，请用直尺和圆规作一条直线，把分割成两个等腰三角形（不写作法，但须保留作图痕迹）．‎ ‎（2）已知内角度数的两个三角形如图2、图3所示．请你判断，能否分别画一条直线把它们分割成两个等腰三角形？若能，请写出分割成的两个等腰三角形顶角的度数．‎ ‎（第21题）‎ A B C 图1‎ A B C 图2‎ ‎24°‎ ‎24°‎ ‎84°‎ A B C 图3‎ ‎104°‎ ‎52°‎ 答案：解：（1）如图，直线即为所求 B C A M C B A M 或 ‎（作图正确，不写结论不扣分）‎ ‎（2）图2能画一条直线分割成两个等腰三角形，‎ 分割成的两个等腰三角形的顶角分别是和．‎ 图3不能分割成两个等腰三角形．‎ ‎①标准纸“2开”纸、“4开”纸、“8开”纸、“16开”纸……都是矩形．‎ ‎②本题中所求边长或面积都用含的代数式表示．‎ ‎26．(2008年宁波市)如图1，把一张标准纸一次又一次对开，得到“2开”纸、“4开”纸、“8开”纸、“16开”纸…．已知标准纸的短边长为．‎ ‎（1）如图2，把这张标准纸对开得到的“16开”张纸按如下步骤折叠：‎ 第一步 将矩形的短边与长边对齐折叠，点落在上的点处，铺平后得折痕；‎ 第二步 将长边与折痕对齐折叠，点正好与点重合，铺平后得折痕．‎ 则的值是 ，的长分别是 ， ．‎ ‎（2）“2开”纸、“4开”纸、“8开”纸的长与宽之比是否都相等？若相等，直接写出这个比值；若不相等，请分别计算它们的比值．‎ ‎（3）如图3，由8个大小相等的小正方形构成“”型图案，它的四个顶点分别在“16开”纸的边上，求的长．‎ A B C D B C A D E G H F F E ‎4开 ‎2开 ‎8开 ‎16开 图1‎ 图2‎ 图3‎ ‎（第26题）‎ a ‎（4）已知梯形中，，，，且四个顶点都在“4开”纸的边上，请直接写出2个符合条件且大小不同的直角梯形的面积．‎