2011年平谷区初三数学一模试题及答案 11页

平谷区2010～2011学年度第二学期初三第一次统一练习 ‎ 数 学 试 卷 （120分钟）2011.4‎ 考生须知 ‎1.试卷分为试题和答题卡两部分，所有试题均在答题卡上作答，在试卷上作答无效。‎ ‎2.答在试卷和答题卡上认真填写学校名称、姓名和准考证好。‎ ‎3.在答题卡上，选择题、作图题用2B铅笔作答，其他试题用黑色字迹签字笔作答。‎ ‎4.修改时，用塑料橡皮擦干净，不得使用涂改液。请保持卡面清洁，不要折叠。‎ 一、选择题（本题共8个小题，每小题4分，共32分）‎ 在下列各题的四个备选答案中，只有一个是正确的．‎ ‎1．的相反数是 A． B． C． D．‎ ‎2．北京市2010年暨“十一五”期间国民经济和社会发展统计公报显示，2010年末，全市共有公共图书馆25个，总藏量44 510 000册．将44 510 000用科学记数法表示应为 A． B． C． D．‎ ‎3．如图，已知AB∥CD，∠C=35°，BC平分∠ABE，则∠ABE的度数是 A．17.5° B．35° C．70° D．105°‎ ‎4．下列运算正确的是 A． B． C． D．‎ ‎5．某男子排球队20名队员的身高如下表：‎ 身高（cm）‎ ‎180‎ ‎186‎ ‎188‎ ‎192‎ ‎208‎ 人数（个）‎ ‎4‎ ‎6‎ ‎5‎ ‎3‎ ‎2‎ 则此男子排球队20名队员的身高的众数和中位数分别是（单位：cm）‎ A．186，186 B．186，‎187 ‎‎ C．208，188 D．188，187‎ ‎6．把多项式分解因式，结果正确的是 蓝 蓝 红 红 红 黄 A． B． C． D．‎ ‎7．如图，一个可以自由转动的转盘被等分成6个扇形区域，并涂上了 相应的颜色，转动转盘，转盘停止后，指针指向红色区域的概率是 Ａ． Ｂ． Ｃ． Ｄ． ‎ ‎8．如图，是的直径，弦，是弦的中点，‎ ‎．若动点以的速度从点出发沿着 方向运动，设运动时间为，连结，‎ 当是直角三角形时，（s）的值为 ‎ ‎ A． B．‎1 ‎‎ C．或1 D．或1 或 ‎ 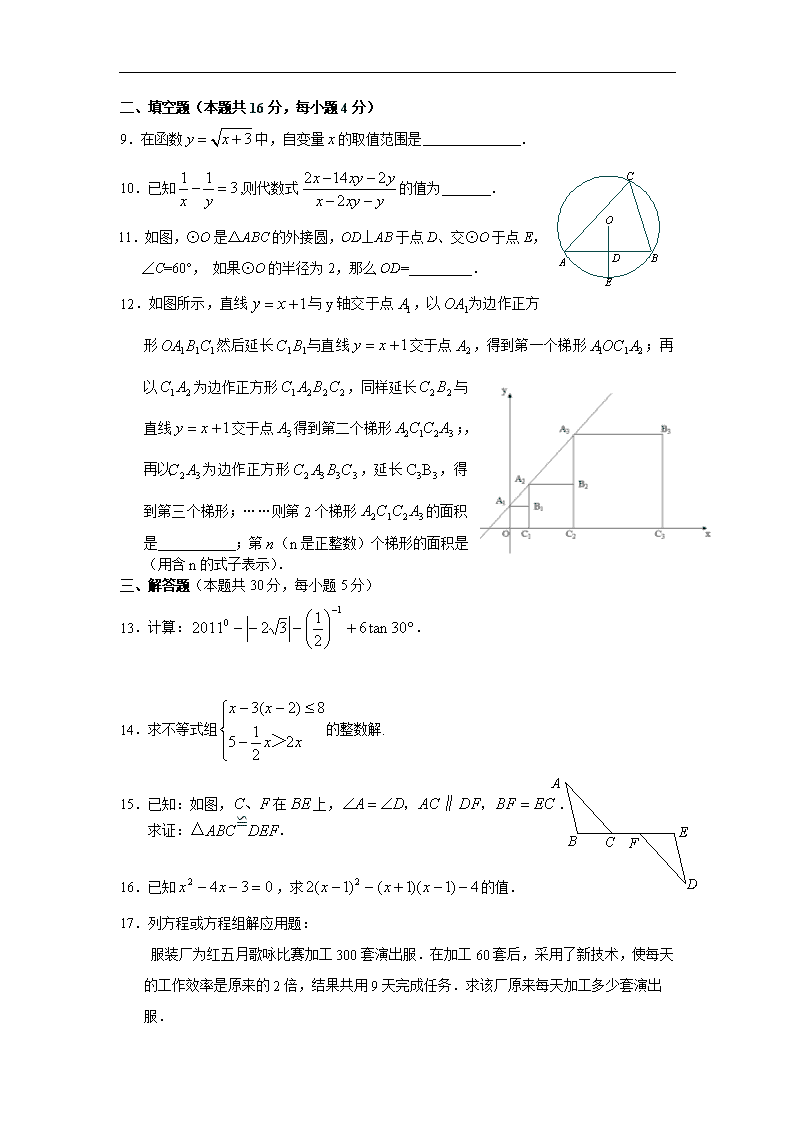二、填空题（本题共16分，每小题4分）‎ ‎9．在函数中，自变量的取值范围是 ．‎ ‎10．已知,则代数式的值为 ．‎ ‎11．如图，⊙O是△ABC的外接圆，OD⊥AB于点D、交⊙O于点E， ∠C=60°， 如果⊙O的半径为2，那么OD= ．‎ ‎12．如图所示，直线与y轴交于点，以为边作正方形然后延长与直线交于点，得到第一个梯形；再以为边作正方形，同样延长与直线交于点得到第二个梯形；，再以为边作正方形，延长，得到第三个梯形；……则第2个梯形的面积是 ；第（n是正整数）个梯形的面积是 （用含n的式子表示）．‎ 三、解答题（本题共30分，每小题5分） ‎ ‎13．计算：．‎ ‎14．求不等式组的整数解.‎ A B C F E D ‎15．已知：如图，在上，．‎ 求证：△ABC≌DEF．‎ ‎16．已知，求的值．‎ ‎17．列方程或方程组解应用题：‎ 服装厂为红五月歌咏比赛加工300套演出服．在加工60套后，采用了新技术，使每天的工作效率是原来的2倍，结果共用9‎ 天完成任务．求该厂原来每天加工多少套演出服．‎ ‎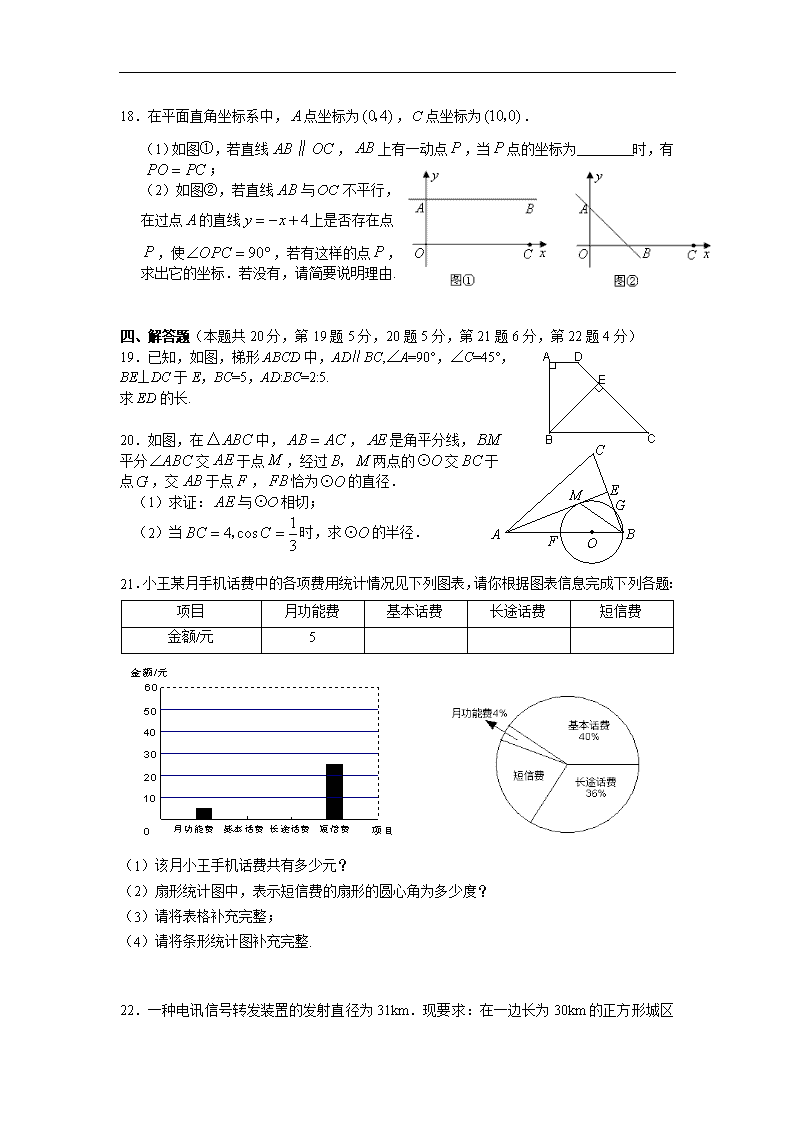18．在平面直角坐标系中，点坐标为，点坐标为．‎ ‎（1）如图①，若直线，上有一动点，当点的坐标为　　　　时，有；‎ ‎（2）如图②，若直线与不平行，‎ 在过点的直线上是否存在点 ‎，使，若有这样的点，‎ 求出它的坐标．若没有，请简要说明理由.‎ 四、解答题（本题共20分，第19题5分，20题5分，第21题6分，第22题4分）‎ ‎19．已知，如图，梯形ABCD中，AD∥BC,∠A=90°，∠C=45°，‎ BE⊥DC于E，BC=5，AD:BC=2:5.‎ 求ED的长.‎ O B G E C M A F ‎20．如图，在中，，是角平分线，‎ 平分交于点，经过两点的交于 点，交于点，恰为的直径．‎ ‎（1）求证：与相切；‎ ‎（2）当时，求的半径．‎ ‎21．小王某月手机话费中的各项费用统计情况见下列图表，请你根据图表信息完成下列各题：‎ 项目 月功能费 基本话费 长途话费 短信费 金额/元 ‎5‎ ‎（1）该月小王手机话费共有多少元？‎ ‎（2）扇形统计图中，表示短信费的扇形的圆心角为多少度？‎ ‎（3）请将表格补充完整；‎ ‎（4）请将条形统计图补充完整.‎ ‎22．一种电讯信号转发装置的发射直径为‎31km．现要求：在一边长为‎30km的正方形城区选择若干个安装点，每个点安装一个这种转发装置，使这些装置转发的信号能完全覆盖这个城市．问：‎ ‎（1）能否找到这样的4个安装点，使得这些点安装了这种转发装置后能达到预设的要求？在图1中画出安装点的示意图，并用大写字母M、N、P、Q表示安装点；‎ ‎（2）能否找到这样的3个安装点，使得在这些点安装了这种转发装置后能达到预设的要求？在图2中画出示意图说明，并用大写字母M、N、P表示安装点，用计算、推理和文字来说明你的理由．‎ 图1‎ A B C D 图2‎ A B C D 图2‎ A B C D 图1‎ A B C D ‎ 五、解答题 （本题共22分，第23题7分，第24题7分，第25题8分） ‎ ‎23．已知二次函数的图象经过点，和，反比例函数（x＞0）的图象经过点（1，2）．‎ ‎（1）求这两个二次函数的解析式，并在给定的直角坐标系中作出这两个函数的图象；‎ ‎（2）若反比例函数（）的图象与二次函数）的图象在第一象限内交于点，落在两个相邻的正整数之间．请你观察图象写出这两个相邻的正整数；‎ ‎（3）若反比例函数（）的图象与二次函数的图象在第一象限内的交点为，点的横坐标满足，试求实数的取值范围．‎ ‎24．已知点A，B分别是两条平行线，上任意两点，C是直线上一点，且 ‎∠ABC=90°，点E在AC的延长线上,BC＝AB (k≠0).‎ ‎（1）当＝1时，在图（1）中，作∠BEF＝∠ABC，EF交直线于点F.，写出线段EF与EB的数量关系，并加以证明；‎ ‎（2）若≠1，如图(2)，∠BEF＝∠ABC，其它条件不变，探究线段EF与EB的数量关系，并说明理由．‎ ‎25．已知：抛物线经过坐标原点．‎ ‎（1）求抛物线的解析式和顶点B的坐标；‎ ‎（2）设点A是抛物线与轴的另一个交点，试在轴上确定一点P，使PA+PB 最短，并求出点P的坐标；‎ ‎（3）过点A作AC∥BP交轴于点C，求到直线AP、AC、CP距离相等的点的坐标．‎ 平谷区2010～2011学年度第二学期初三第一次统一练习 ‎ 数学试卷参考答案及评分参考 2011.4‎ 一、选择题（本题共8个小题，每小题4分，共32分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答案 D B C A B D C D 二、填空题（本题共16分，每小题4分）‎ 题号 ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 ‎4‎ ‎1‎ ‎6（2分）‎ 或 （2分）‎ 三、解答题（本题共30分，每小题5分） ‎ ‎13．解：‎ ‎= …………………………………………………………………….4分 ‎= ………………………………………………………………………………………5分 ‎14．解：由 得，………………………………………………….1 分 由 得，……………………………………………………. 2分 ‎. ……………………………………………………………………4分 ‎ 不等式组的整数解是 . ………….. ……………………………………………5分 ‎15．证明：，‎ A B C F E D ‎.………………………………1分 ‎． …………………………….2分 又，‎ ‎，即．………..3分 在△ABC与△DEF中，‎ ‎ …………………………………………………………………4分 ‎．………………………………………………………………………5分 ‎16．解：‎ ‎= …………………………….…………………………...2分 ‎= …………………………………………….……………………………..4分 ‎∴ 原式==…………………….………………………………5分 ‎17．解：设服装厂原来每天加工套演出服．……………………………………….1分 根据题意，得 ． ………………………………………………….2分 解 得 ．………………………………………………………………………3分 经检验，是原方程的根．………………………………………………………..4分 答：服装厂原来每天加工20套演出服．……………………………………………….5分 ‎18．解：（1）……………………………………………………………………….2分 ‎（2）设，‎ 连接，过作于，‎ 于，……………………………………3分 因为，‎ ‎　　，‎ ‎　　，‎ 所以.‎ ‎　　，‎ ‎　　，．………………………………………………………………….4分 所以坐标或．………………………………………………………....5分 四、解答题（本题共20分，第19题5分，20题5分，第21题6分，第22题4分）‎ ‎19．解：作DF⊥BC于F,EG⊥BC于G. ……………………………………………1分 ‎∵∠A=90°，AD∥BC ‎∴ 四边形ABFD是矩形.‎ ‎∵ BC=5,AD:BC=2:5.‎ ‎∴ AD=BF=2. ………………………………………..2分 ‎∴ FC=3.‎ 在Rt△DFC中，‎ ‎∵ ∠C=45°，‎ ‎∴ DC=.…………………………………………3分 在Rt△BEC中，‎ ‎∴ EC=……………………………………………….……………………………....4分 ‎∴ DE=……………………………………………………………….5分 ‎20．解：（1）证明：连结，则．‎ ‎∴ ．‎ O B G E C M A F ‎1‎ ‎2‎ ‎3‎ ‎∵ 平分．‎ ‎∴ ．‎ ‎∴ ．‎ ‎∴ ．‎ ‎∴ ．…………………………..1分 在中，‎ ‎∵ ，是角平分线，‎ ‎∴ ．………………………………………………………………………..….2分 ‎∴ ．‎ ‎∴ ．‎ ‎∴ ．‎ ‎∴ 与相切．………………………………………………………………………3分 ‎（2）解：在中，，是角平分线，‎ ‎∴．‎ ‎∵，‎ ‎∴,‎ 在中，，‎ ‎∴．………………………………………………………………….4分 设的半径为，则．‎ ‎∵，‎ ‎∴．‎ ‎∴ ．‎ ‎∴ ．‎ 解得．∴ 的半径为 ‎．………………………………………………………….5分 ‎21．解：‎ ‎（1）总话费125元………….1分 ‎（2）72°……………………..2分 ‎（3）基本话费50；………….3分 长途话费45；……………4分 短信费 25………………...5分 ‎（4）……………………………6分 ‎22．解：（1）(2分) （2）（画图正确给1分）‎ A D C B 图1‎ P Q M N ‎（2）‎ 图2‎ ‎（图案设计不唯一）‎ 将原正方形分割成如图2中的3个矩形，使得BE=OD=OC．将每个装置安装在这些矩形的对角线交点处，设，则，．由BE=OD，‎ 得，，，‎ 即如此安装3个这种转发装置，也能达到预设要求． 4分 或：将原正方形分割成如图2中的3个矩形，使得，是的中点，将每个装置安装在这些矩形的对角线交点处，则，，‎ ‎ ∴ ，如此装三个这个转发装置，能达到预设要求．‎ 五、解答题 （本题共22分，第23题7分，第24题7分，第25题8分）‎ ‎23．解：（1）把，和分别代入 解方程组，得 ………………1分 ‎∴ 抛物线解析式为…...2分 ‎∵ 反比例函数的图象经过点（1，2），‎ ‎∴ k=2. ∴ ……………….…...3分 ‎(2)正确的画出二次函数和反比例函数在第一象限内的图象 ……………………….4分 由图象可知，这两个相邻的正整数为1与2. ………………………………………5分 ‎(3)由函数图象或函数性质可知：当2＜x＜3时，对y=，y随着x的增大而增大，对y2=（k＞0），y2随着x的增大而减小.因为A（x0,y0）为二次函数图象与反比例函数图象的交点，所以当x0=2时，由反比例函数图象在二次函数的图象上方，得y2＞y.‎ 即＞，‎ 解得k＞5. …………………………………………………………………………6分 同理，当x0=3时，由二次函数的图象在反比例函数图象上方的，得y＞y2，‎ 即＞，解得k＜18. ‎ 所以k的取值范围为5＜k＜18. ………………………………………………7分 ‎24．解：（1）正确画出图形………………………………………….…………..1分 图（1）‎ ‎． ……………………………………………2分 证明：如图（1），在直线上截取，连结．‎ ‎，，．‎ ‎，.‎ ‎，，．‎ ‎，． 3分 ‎，．……………………………4分 ‎，．‎ ‎．又，‎ ‎．‎ 图(2)‎ A B C M E N m n F ‎.‎ ‎．…………………….………………………………..5分 ‎（2）．‎ 说明：如图(2)，过点作，，垂足为．‎ ‎．‎ ‎，，‎ ‎．‎ 四边形为矩形．‎ ‎，．‎ ‎,‎ ‎．‎ ‎． 6分 ‎．．‎ 在和中，，‎ ‎． ………………………………………………………………………………7分 ‎25．解：（1）∵ 抛物线经过坐标原点,‎ ‎∴ =0. 解得 .‎ ‎∵ ，∴ ∴ …1分 ‎∴ . ………………………….2分 ‎（2）令，得=0，‎ 解得 . ∴ ………..3分 ‎∴点A关于轴的对称点的坐标为.‎ 联结，直线与轴的交点即为所求点P.‎ 可求得直线的解析式：. ∴ ……………………………4分 ‎（3）到直线AP、AC、CP距离相等的点有四个．‎ 如图，由勾股定理得，所以△PAC为等边三角形．‎ 易证轴所在直线平分∠PAC，BP是△PAC的一个外角的平分线．作∠PCA的平分线，交轴于点，交过A点的平行线于y轴的直线于点，作△PAC的∠PCA相邻外角的平分线，交于点，反向延长C交轴于点．可得点就是到直线AP、AC、CP距离相等的点．可证△AP 、△AC、 △PC 均为等边三角形．可求得：①，所以点M1的坐标为；…………5分 ‎②，所以点M2的坐标为；………………………………....6分 ‎③点M3与点M2关于x轴对称，所以点M3的坐标为；………………..…..7分 ‎④点与点A关于y轴对称，所以点的坐标为．‎ 综上所述，到直线AP、AC、CP距离相等的点的坐标分别为,,,．…………………………….. 8分