中考数学全程复习方略第二十三讲直角三角形的边角关系课件 54页

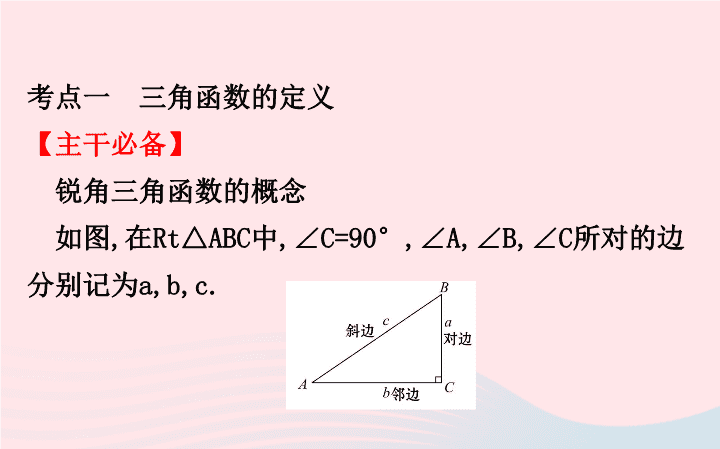
第二十三讲　 直角三角形的边角关系 考点一　三角函数的定义 【 主干必备 】 　锐角三角函数的概念 　如图 , 在 Rt△ABC 中 ,∠C=90°,∠A,∠B,∠C 所对的边分别记为 a,b,c. 1. 正弦 :sin A=            =___.  2. 余弦 :cos A=            =___.  3. 正切 :tan A=            =___.  锐角 A 的正弦、余弦、正切统称∠ A 的锐角三角函数 . 【 微点警示 】 (1) 注意自变量 : 锐角三角函数的自变量是角度 , 其取值范围是 :0°<α<90°. (2) 注意锐角三角函数的值 : 当∠ A 为锐角时 ,00. 【 核心突破 】 例 1(2019· 甘肃中考 ) 在 Rt△ABC 中 ,∠C=90°, tan A= , 则 cos B=___.  【 明 · 技法 】 根据定义求三角函数值的方法 (1) 分清直角三角形中的斜边与直角边 . (2) 正确地表示出直角三角形的三边长 , 常设某条直角边长为 k( 有时也可以设为 1), 在求三角函数值的过程中约去 k. (3) 正确应用勾股定理求第三条边长 . (4) 应用锐角三角函数定义 , 求出三角函数值 . (5) 求一个角的三角函数值时 , 若不易直接求出 , 也可把这个角转化成和它相等且位于直角三角形中的角 . 【 题组过关 】 1.( 概念应用题 ) 如图 , 在 Rt△ABC 中 ,∠ACB=90°,AB⊥CD 于点 D, 下 列各组线段的比不能表示 sin∠BCD 的是 ( 　 　 ) C 2.(2019· 宜昌中考 ) 如图 , 在 5×4 的正 方形网格中 , 每个小正方形的边长都是 1,△ABC 的顶点都在这些小正方形的 顶点上 , 则 sin∠BAC 的值为世纪金榜导学号 ( 　 　 ) D 3.(2019· 眉山中考 ) 如图 , 在 Rt△ABC 中 ,∠B=90°,AB=5,BC=12, 将△ ABC 绕 点 A 逆时针旋转得到△ ADE, 使得点 D 落 在 AC 上 , 则 tan∠ECD 的值为 ___. 世纪金榜导学号  4. 如图 , 在平面直角坐标系中 , 直线 OA 过点 (2,1), 则 tan α 的值是   ___. 世纪金榜导学号  考点二　特殊角的三角函数值 【 主干必备 】 特殊角的三角函数值 α 30° 45° 60° sin α ___ ___ ___ α 30° 45° 60° cos α ___ ___ ___ tan α ___ ___ ___ 1 【 微点警示 】 (1) 互余两角三角函数之间的关系 : 由上表可得 , 当两角互余时 , 一角的正弦值等于另一个角的余弦值 , 即当∠ A+∠B=90° 时 , 则 sin A=cos B,cos A=sin B. (2) 锐角三角函数值的变化规律 : 在锐角范围内 , sin α 、 tan α 的值随 α 的增大而增大 ,cos α 的值随 α 的增大而减小 . 【 核心突破 】 例 2 【 原型题 】 (2018· 青海中考 ) 在△ ABC 中 , 若 =0, 则∠ C 的度数是 ___________.  90° 【 变形题 1】 ( 变换条件 ) 在△ ABC 中 , 若 =0, 则∠ C 的度数是 ___________.  【 变形题 2】 ( 变换结论 ) 在△ ABC 中 , 若 =0, 则 的值为 ________.  90° 1 【 明 · 技法 】 熟记特殊角的三角函数值的两种方法 (1) 按值的变化 :30°,45°,60° 角的正余弦的分母都 是 2, 正弦的分子分别是 1, , , 余弦的分子分别是 , ,1, 正切分别是 ,1, . (2) 特殊值法 : ① 在直角三角形中 , 设 30° 角所对的直角边为 1, 那么三 边长分别为 1, ,2; ② 在直角三角形中 , 设 45° 角所对的直角边为 1, 那么 三边长分别为 1,1, . 【 题组过关 】 1.(2019· 天津中考 )2sin 60° 的值等于 ( 　 　 ) A.1 B. C. D.2 C 2. 当∠ A 为锐角 , 且