鄂尔多斯专版2020中考数学复习方案第四单元三角形第17课时全等三角形课件 32页

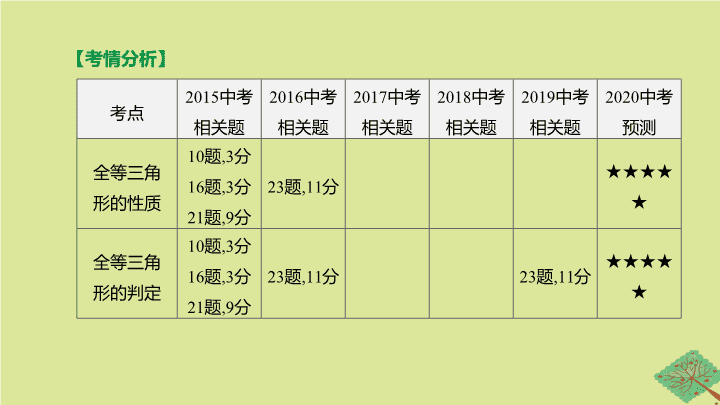
第 17 课时 全等三角形 第四单元　三角形 【 考情分析 】 考点 2015 中考 相关题 2016 中考 相关题 2017 中考 相关题 2018 中考 相关题 2019 中考 相关题 2020 中考 预测 全等三角 形的性质 10 题 ,3 分 16 题 ,3 分 21 题 ,9 分 23 题 ,11 分 ★★★★★ 全等三角 形的判定 10 题 ,3 分 16 题 ,3 分 21 题 ,9 分 23 题 ,11 分 23 题 ,11 分 ★★★★★ 考点一　全等三角形的概念及性质 考点聚焦 1 . 定义 : 能够完全重合的两个三角形叫做全等三角形 . 2 . 性质 : (1) 全等三角形的对应边 ① 　　　　 , 对应角 ② 　　　　 ;(2) 全等三角形的周长 ③ 　　　　 , 面积 ④ 　　　　 ;(3) 全等三角形对应的中线、高线、角平分线、中位线都 ⑤ 　　　　 .  相等 相等 相等 相等 相等 考点二　全等三角形的判定 1. 全等三角形的判定方法 对应相等的元素 三角形是否全等 一 般 三 角 形 两边 一角 两边及其夹角 全等 (SAS) 两边及其中一边的对角 不一定全等 两角 一边 两角及其夹边 全等 (ASA) 两角及其中一角的对边 全等 (AAS) 三角 不一定全等 三边 全等 (SSS) ( 续表 ) 对应相等的元素 三角形是否全等 直角三角形 斜边、直角边 全等 (HL) 总结 　 判定一般三角形全等 , 无论用哪种方法 , 都要有三组元素对应相等 , 且其中最少要有一组对应边相等 题组一　必会题 对点演练 1 . 如图 17-1, 点 D , E 分别在线段 AB , AC 上 , CD 与 BE 相交于点 O , 已知 AB = AC , 再添加以下条件仍不能判定 △ ABE ≌△ ACD 的是 ( 　　 ) A . ∠ B = ∠ C B .AD = AE C .BD = CE D .BE = CD D 图 17-1 2 . 如图 17-2, AE ∥ DF , AE = DF , 要使 △ EAC ≌△ FDB , 需要添加下列选项中的 ( 　　 ) A .AB = CD B .EC = BF C . ∠ A = ∠ D D .AB = BC 图 17-2 A 3 . 如图 17-3,△ ABC ≌△ DEF , 线段 AD =5, DE =3, 则 BD = 　　　　 .  图 17-3 2 题组二　易错题 【 失分点 】 两边和其中一边的对角分别相等的两个三角形不一定全等 . 4 . 不能判定两个三角形全等的是 ( 　　 ) A . 三边对应相等的两个三角形全等 B . 两边及其夹角对应相等的两个三角形全等 C . 两角及其夹边对应相等的两个三角形全等 D . 三个角对应相等的两个三角形全等 D 5 . 如图 17-4, 已知 CD = CA , ∠ 1= ∠ 2, 要使 △ ECD ≌△ BCA , 需添加的条件是 ________ 　 　 ( 只写出一个条件即可 ) .  图 17-4 ( 或∠ D = ∠ A 或∠ E = ∠ B ) CE = CB 考向一　全等三角形的判定和性质 例 1 [2019· 安顺 ] 如图 17-5, 点 B , F , C , E 在一条直线上 , AB ∥ DE , AC ∥ DF , 那么添加下列一个条件后 , 仍无法判断 △ ABC ≌△ DEF 的是 ( 　　 ) A .AB = DE B . ∠ A = ∠ D C .AC = DF D .BF = EC 图 17-5 [ 答案 ] B 　 [ 解析 ] ∵ AB ∥ DE , AC ∥ DF , ∴∠ B = ∠ E , ∠ ACB = ∠ DFE , A . 添加 AB = DE 可利用 AAS 判断 △ ABC ≌△ DEF , 故此选项不合题意 ; B . 添加∠ A = ∠ D 无法判断 △ ABC ≌△ DEF , 故此选项符合题意 ; C . 添加 AC = DF 可利用 AAS 判断 △ ABC ≌△ DEF , 故此选项不合题意 ; D . 添加 BF = EC 可得 BC = EF , 可利用 ASA 判断 △ ABC ≌△ DEF , 故此选项不合题意 . 故选 B . 例 2 [2019· 无锡 ] 如图 17-6, 在 △ ABC 中 , AB = AC , 点 D , E 分别在 AB , AC 上 , BD = CE , BE , CD 相交于点 O. 求证 : (1)△ DBC ≌△ ECB ; (2) OB = OC. 图 17-6 【 方法点析 】 全等三角形的基本模型 一、轴对称型 图 17-7 二、旋转对称型 图 17-8 三、平移型 图 17-9 | 考向精练 | 1 . [2019· 临沂 ] 如图 17-10, D 是 AB 上一点 , DF 交 AC 于点 E , DE = FE , FC ∥ AB. 若 AB = 4, CF =3, 则 BD 的长是 ( 　　 ) A . 0 . 5 B . 1 C . 1 . 5 D . 2 图 17-10 [ 答案 ] B 图 17-11 [ 答案 ] 4 3 . [2019· 黄冈 ] 如图 17-12, 四边形 ABCD 是正方形 , E 是 CD 边上任意一点 , 连接 AE , 作 BF ⊥ AE , DG ⊥ AE , 垂足分别为 F , G. 求证 : BF - DG = FG. 图 17-12 证明 : 在 △ ABF 和 △ DAG 中 , ∵ BF ⊥ AE , DG ⊥ AE , ∴∠ AFB = ∠ DGA =90° . 又∠ DAG + ∠ FAB = ∠ DAG + ∠ ADG =90°, ∴∠ FAB = ∠ GDA. 又 AB = AD , ∴ △ ABF ≌△ DAG. ∴ BF = AG , AF = DG. ∴ BF - DG = AG - AF = FG. 考向二　全等三角形的综合问题 例 3 [2016· 呼和浩特 ] 如图 17-13,△ ACB 和 △ ECD 都是等腰直角三角形 , ∠ ACB = ∠ ECD =90°, D 为 AB 边上一点 . 求证 : (1)△ ACE ≌△ BCD ; (2)2 CD 2 = AD 2 + DB 2 . 图 17-13 例 3 [2016· 呼和浩特 ] 如图 17-13,△ ACB 和 △ ECD 都是等腰直角三角形 , ∠ ACB = ∠ ECD =90°, D 为 AB 边上一点 . 求证 : (2)2 CD 2 = AD 2 + DB 2 . 证明 : (2) ∵ △ ACB 是等腰直角三角形 , ∴∠ B = ∠ BAC =45° . ∵ △ ACE ≌△ BCD , ∴∠ CAE = ∠ B =45°, ∴∠ DAE = ∠ CAE + ∠ BAC =45°+45°=90°, ∴ AD 2 + AE 2 = DE 2 . 由 (1) 知 , AE = DB , ∴ AD 2 + DB 2 = DE 2 , 即 2 CD 2 = AD 2 + DB 2 . 图 17-13 | 考向精练 | 1 . 在 △ ABC 中 , ∠ BAC> 90°, ∠ ACB = ∠ ABC = α , 点 D 为 BC 边上任意一点 , 点 E 在 AD 延长线上 , 且 BC = BE. (1) 当 α =30°, 点 D 恰好为 BC 中点时 , 补全图 17-14 ① , 求∠ BEA 的度数 ; (2) 如图② , 若∠ BAE =2 α , 此时恰好 DB = DE , 连接 CE , 求证 :△ ABE ≌△ CEB. 图 17-14 解 :(1) 补全图① , 如图所示 . ∵∠ ACB = ∠ ABC , ∴ AB = AC , ∵ BD = DC , ∴ AE ⊥ BC , ∴ EB = EC , ∠ ADB =90° . ∵∠ ABC =30°, ∴∠ BAE =60° . ∵ BC = BE , ∴ △ BCE 是等边三角形 , ∠ DEB = ∠ DEC , ∴∠ BEA =30° . 1 . 在 △ ABC 中 , ∠ BAC> 90°, ∠ ACB = ∠ ABC = α , 点 D 为 BC 边上任意一点 , 点 E 在 AD 延长线上 , 且 BC = BE. (2) 如图② , 若∠ BAE =2 α , 此时恰好 DB = DE , 连接 CE , 求证 :△ ABE ≌△ CEB. 图 17-14 2 . [2018· 哈尔滨 ] 在四边形 ABCD 中 , 对角线 AC , BD 相交于点 E , 且 AC ⊥ BD , 作 BF ⊥ CD , 垂足为 F , BF 与 AC 交于点 G , ∠ BGE = ∠ ADE. (1) 如图 17-15 ① , 求证 : AD = CD. (2) 如图② , BH 是 △ ABE 的中线 , 若 AE =2 DE , DE = EG , 在不添加任何辅助线的情况下 , 请直接写出图②中的四个三角形 , 使写出的每个三角形的面积都等于 △ ADE 面积的 2 倍 . 图 17-15 解 :(1) 证明 : ∵∠ BGE = ∠ ADE , ∠ BGE = ∠ CGF , ∴∠ ADE = ∠ CGF. ∵ AC ⊥ BD , BF ⊥ CD , ∴∠ ADE + ∠ DAE = ∠ CGF + ∠ GCF , ∴∠ DAE = ∠ GCF , ∴ AD = CD. 2 . [2018· 哈尔滨 ] 在四边形 ABCD 中 , 对角线 AC , BD 相交于点 E , 且 AC ⊥ BD , 作 BF ⊥ CD , 垂足为 F , BF 与 AC 交于点 G , ∠ BGE = ∠ ADE. (2) 如图② , BH 是 △ ABE 的中线 , 若 AE =2 DE , DE = EG , 在不添加任何辅助线的情况下 , 请直接写出图②中的四个三角形 , 使写出的每个三角形的面积都等于 △ ADE 面积的 2 倍 . 图 17-15