鄂尔多斯专版2020中考数学复习方案第三单元函数及其图象第14课时二次函数的实际应用课件 31页

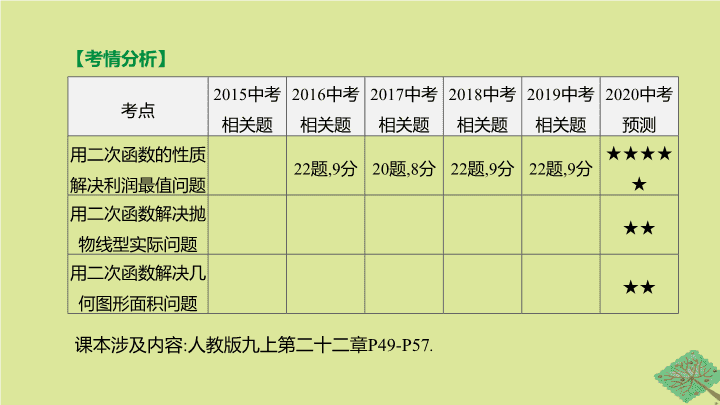
第 14 课时 二次函数的实际应用 第三单元　函数及其图象 【考情分析】 考点 2015中考 相关题 2016中考 相关题 2017中考 相关题 2018中考 相关题 2019中考 相关题 2020中考 预测 用二次函数的性质 解决利润最值问题 22题,9分 20题,8分 22题,9分 22题,9分 ★★★★★ 用二次函数解决抛 物线型实际问题 ★★ 用二次函数解决几 何图形面积问题 ★★ 课本涉及内容:人教版九上第二十二章P49-P57. 基 础 知 识 巩 固 高 频 考 向 探 究 考点一　建立二次函数模型解决问题 考点聚焦 常见类型 关键步骤 抛物线形问题 　建立方便求解析式的平面直角坐标系,找到图象上三点的坐标, 用待定系数法求二次函数的解析式 销售利润问题 　理清各个量之间的关系,找出等量关系求得解析式,根据要求确 定函数的最值或建立方程求解 图形面积问题 　利用几何知识用变量x表示出图形的面积y,根据要求确定函数的 最值或建立方程求解 基 础 知 识 巩 固 高 频 考 向 探 究 【温馨提示】 (1)求函数的最值时,要注意实际问题中自变量的取值限制对最值的影响.若对称 轴的取值不在自变量的取值范围内,则最值在自变量取值的端点处取得. (2)建立平面直角坐标系的原则是易于求二次函数的解析式. 基 础 知 识 巩 固 高 频 考 向 探 究 考点二　图象信息类问题 1.表格类 观察点的特征,验证满足条件的二次函数的解析式及其图象,利用二次函数的性 质求解. 2.图文类 根据图文,借助图形上的关键点,提取信息,建立二次函数模型解题. 基 础 知 识 巩 固 高 频 考 向 探 究 对点演练 题组一　必会题 图14-1 B 基 础 知 识 巩 固 高 频 考 向 探 究 2.如图14-2,一边靠校园围墙(足够长),其他三边用总长为80米的铁栏杆围成一 个矩形花圃,设矩形ABCD的边AB为x米,若要使矩形ABCD的面积最大,则x的长 为 (　　) A.40米 B.30米 C.20米 D.10米 图14-2 C 基 础 知 识 巩 固 高 频 考 向 探 究 4.一个小球向斜上方抛出,它的行进高度y(单位:m)与水平距离x(单位:m)之间的 关系式是y=-x2+4x+1,则小球能到达的最大高度是　　　　m. 5 D 基 础 知 识 巩 固 高 频 考 向 探 究 [答案] 10 基 础 知 识 巩 固 高 频 考 向 探 究 题组二　易错题 【失分点】 求实际问题中的最值时,易忽略自变量取值范围. 6.春节期间,物价局规定某种蔬菜的最低价格为4.1元/千克,最高价格为4.5元/ 千克,小王按4.1元/千克购进,若按购进价出售,则平均每天可卖出200千克,若 价格每上涨0.1元,则每天少卖出20千克.售价定为　　　　元/千克时,每天获 利最大,最大利润为　　　　元.  基 础 知 识 巩 固 高 频 考 向 探 究 [答案] 4.5　48　 [解析] 设售价为x元/千克,则每千克获利(x-4.1)元. ∵价格每上涨0.1元,每天少卖出20千克, ∴每天的销售量为200-20(x-4.1)×10=-200x+1020. 设每天获利W元,则W=(-200x+1020)(x-4.1)=-200x2+1840x-4182=-2(100x2-920x+ 2116)+4232-4182=-2(10x-46)2+50. ∵a=-2<0,∴当x≤4.6时,W随x的增大而增大. ∵物价局规定该种蔬菜的最低价格为4.1元/千克,最高价格为4.5元/千克, ∴4.1≤x≤4.5, ∴当x=4.5时,W有最大值,即获利最大, 最大利润为-2×(10×4.5-46)2+50=-2+50=48(元). 基 础 知 识 巩 固 高 频 考 向 探 究 [答案] 24 基 础 知 识 巩 固 高 频 考 向 探 究 考向一　用二次函数解决抛物线型的实际问题 例1 有一隧道,内设双行线公路,同方向有两个车道(共有四个车道),每个车道宽 为3 m,此隧道的截面由一个长方形和部分抛物线构成.如图14-3,隧道高8 m,宽 16 m,为了保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高 度之差至少为0.25 m,靠近中轴线的车道为快车道,两侧的车道为慢车道,求当车 辆通过隧道时,慢车道的限制高度(用分数表示). 图14-3 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 【方法点析】解决此类问题的关键是选择合理的位置建立直角坐标系,建立直 角坐标系的原则:①所建立的直角坐标系要使求出的二次函数的解析式比较简 单;②使已知点所在的位置适当(如在x轴,y轴,原点,抛物线上等),方便求二次函 数的解析式和进行之后的计算. 基 础 知 识 巩 固 高 频 考 向 探 究 考向二　二次函数在销售、加工等问题中的应用 例2 某衬衣店将进价为30元/件的一种衬衣以40元/件售出,平均每月能售出600 件,调查表明:这种衬衣售价每上涨1元,其销售量将减少10件. (1)写出月销售利润y(单位:元)与售价x(单位:元/件)之间的函数解析式. (2)当销售价定为45元/件时,计算月销售量和销售利润. (3)衬衣店想在月销售量不少于300件的情况下,使月销售利润达到10000元,销 售价应定为多少? (4)当销售价定为多少时会获得最大利润?求出最大利润. 解: (1)由题意可得y=(x-30)[600-10(x-40)]=-10x2+1300x-30000. 基 础 知 识 巩 固 高 频 考 向 探 究 例2 某衬衣店将进价为30元/件的一种衬衣以40元/件售出,平均每月能售出600 件,调查表明:这种衬衣售价每上涨1元,其销售量将减少10件. (2)当销售价定为45元/件时,计算月销售量和销售利润. 解: (2)当x=45时,月销售量为600-10×(45-40)=550(件), 销售利润为y=-10×452+1300×45-30000=8250(元). 基 础 知 识 巩 固 高 频 考 向 探 究 例2 某衬衣店将进价为30元/件的一种衬衣以40元/件售出,平均每月能售出600 件,调查表明:这种衬衣售价每上涨1元,其销售量将减少10件. (3)衬衣店想在月销售量不少于300件的情况下,使月销售利润达到10000元,销 售价应定为多少? 解: (3)当y=10000时,10000=-10x2+1300x-30000, 解得x1=50,x2=80. 当x=80时,600-10×(80-40)=200<300,不合题意,舍去, 当x=50时,600-10×(50-40)=500>300,符合题意. 故销售价应定为50元/件. 基 础 知 识 巩 固 高 频 考 向 探 究 例2 某衬衣店将进价为30元/件的一种衬衣以40元/件售出,平均每月能售出600 件,调查表明:这种衬衣售价每上涨1元,其销售量将减少10件. (4)当销售价定为多少时会获得最大利润?求出最大利润. 解: (4) y=-10x2+1300x-30000=-10(x-65)2+12250, 故当销售价定为65元/件时,会获得最大利润,最大利润为12250元. 基 础 知 识 巩 固 高 频 考 向 探 究 【方法点析】解决此类问题的关键:①列出二次函数的解析式,并根据自变量 的实际意义确定自变量的取值范围.②配方或利用公式求顶点.③检查顶点横 坐标是否在自变量的取值范围内.若在,则函数在顶点处取得最大值或最小值; 若不在,则在自变量的取值范围内的两端点处,根据函数增减性确定最值. 基 础 知 识 巩 固 高 频 考 向 探 究 | 考向精练 | 1.[2018·鄂尔多斯22题]牧民巴特尔在生产和销售某种奶食品时,采取客户先网 上订购,然后由巴特尔付费选择甲或乙快递公司送货上门的销售方式.甲快递公 司运送2千克,乙快递公司运送3千克共需运费42元;甲快递公司运送5千克,乙快 递公司运送4千克共需运费70元. (1)求甲、乙两个快递公司每千克的运费分别是多少元. 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 1.[2018·鄂尔多斯22题]牧民巴特尔在生产和销售某种奶食品时,采取客户先网 上订购,然后由巴特尔付费选择甲或乙快递公司送货上门的销售方式.甲快递公 司运送2千克,乙快递公司运送3千克共需运费42元;甲快递公司运送5千克,乙快 递公司运送4千克共需运费70元. 基 础 知 识 巩 固 高 频 考 向 探 究 解: (2) ∵6<10,∴选择甲快递公司,且费用为每千克6元. 设获得利润w元. 当0192,∴巴特尔每天生产量为7千克时获得利润最大,最大利润为196元. 基 础 知 识 巩 固 高 频 考 向 探 究 2.[2017·鄂尔多斯20题]某商场试销A,B两种型号的台灯,下表是两次进货情况 统计: (1)求A,B两种型号台灯的进价分别为多少元. (2)经试销发现,A型号台灯售价x(元/盏)与销售数量y(盏)满足关系式2x+y=140. 此商场决定两种型号台灯共进货100盏,并一周内全部售出,若B型号台灯的售 价定为20元/盏,求A型号台灯的售价定为多少时,商场可获得最大利润,并通过 计算说明商场获得最大利润时的进货方案. 　 进货情况 进货次数　 进货数量/盏 进货资金/元 A B 第一次 5 3 230 第二次 10 4 440 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 2.[2017·鄂尔多斯20题]某商场试销A,B两种型号的台灯,下表是两次进货情况 统计: (2)经试销发现,A型号台灯售价x(元/盏)与销售数量y(盏)满足关系式2x+y=140. 此商场决定两种型号台灯共进货100盏,并一周内全部售出,若B型号台灯的售 价定为20元/盏,求A型号台灯的售价定为多少时,商场可获得最大利润,并通过 计算说明商场获得最大利润时的进货方案. 　 进货情况 进货次数　 进货数量/盏 进货资金/元 A B 第一次 5 3 230 第二次 10 4 440 基 础 知 识 巩 固 高 频 考 向 探 究 解: (2)设商场获得的利润为W元.根据题意,得 W=(x-40)·y+(20-10)·(100-y) =(x-40)(140-2x)+(20-10)[100-(140-2x)] =-2x2+240x-6000 =-2(x-60)2+1200, ∴当x=60时,W取得最大值. 把x=60代入2x+y=140,得y=20(符合题意), 100-20=80(盏). 答:当A型号台灯的售价定为60元/盏时,商场可获得最大利润,此时进货方案为 商场进A型号台灯20盏,B型号台灯80盏. 基 础 知 识 巩 固 高 频 考 向 探 究 考向三　二次函数在几何图形中的应用 例3 某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外 三边由长为30米的篱笆围成.已知墙长为18米(如图14-4),设这个苗圃园垂直于 墙的一边长为x米. (1)若苗圃园的面积为72平方米,求x; (2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗? 如果有,求出最大值和最小值;如果没有,请说明理由. 图14-4 解: (1)根据题意,得(30-2x)x=72, 解得x=3或x=12. ∵30-2x≤18,∴x≥6,∴x=12. 基 础 知 识 巩 固 高 频 考 向 探 究 例3 某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外 三边由长为30米的篱笆围成.已知墙长为18米(如图14-4),设这个苗圃园垂直于 墙的一边长为x米. (2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗? 如果有,求出最大值和最小值;如果没有,请说明理由. 图14-4 基 础 知 识 巩 固 高 频 考 向 探 究