2019湖南省怀化市中考数学试卷 解析版 18页

‎2019年湖南省怀化市中考数学试卷 一、选择题（每小题4分，共40分；每小題的四个选项中只有一项是正确的，请将正确选项的代号填涂在答题卡的相应位置上）‎ ‎1．（4分）下列实数中，哪个数是负数（　　）‎ A．0 B．3 C． D．﹣1‎ ‎2．（4分）单项式﹣5ab的系数是（　　）‎ A．5 B．﹣5 C．2 D．﹣2‎ ‎3．（4分）怀化位于湖南西南部，区域面积约为27600平方公里，将27600用科学记数法表示为（　　）‎ A．27.6×103 B．2.76×103 C．2.76×104 D．2.76×105‎ ‎4．（4分）抽样调查某班10名同学身高（单位：厘米）如下：160，152，165，152，160，160，170，160，165，159．则这组数据的众数是（　　）‎ A．152 B．160 C．165 D．170‎ ‎5．（4分）与30°的角互为余角的角的度数是（　　）‎ A．30° B．60° C．70° D．90°‎ ‎6．（4分）一元一次方程x﹣2＝0的解是（　　）‎ A．x＝2 B．x＝﹣2 C．x＝0 D．x＝1‎ ‎7．（4分）怀化是一个多民族聚居的地区，民俗文化丰富多彩．下面是几幅具有浓厚民族特色的图案，其中既是轴对称图形又是中心对称图形的是（　　）‎ A． B． ‎ C． D．‎ ‎8．（4分）已知∠α为锐角，且sinα＝，则∠α＝（　　）‎ A．30° B．45° C．60° D．90°‎ ‎9．（4分）一元二次方程x2+2x+1＝0的解是（　　）‎ A．x1＝1，x2＝﹣1 B．x1＝x2＝1 C．x1＝x2＝﹣1 D．x1＝﹣1，x2＝2‎ ‎10．（4分）为了落实精准扶贫政策，某单位针对某山区贫困村的实际情况，特向该村提供优质种羊若干只．在准备配发的过程中发现：公羊刚好每户1只；若每户发放母羊5只，则多出17只母羊，若每户发放母羊7只，则有一户可分得母羊但不足3只．这批种羊共（　　）只．‎ A．55 B．72 C．83 D．89‎ 二、填空题（每小题4分，共24分；请将答案直接填写在答题卡的相应位置上）‎ ‎11．（4分）合并同类项：4a2+6a2﹣a2＝　 　．‎ ‎12．（4分）因式分解：a2﹣b2＝　 　．‎ ‎13．（4分）计算：﹣＝　 　．‎ ‎14．（4分）若等腰三角形的一个底角为72°，则这个等腰三角形的顶角为　 　．‎ ‎15．（4分）当a＝﹣1，b＝3时，代数式2a﹣b的值等于　 　．‎ ‎16．（4分）探索与发现：下面是用分数（数字表示面积）砌成的“分数墙”，则整面“分数墙”的总面积是　 　．‎ 三、解答题（本大题共7小题，共86分）‎ ‎17．（8分）计算：（π﹣2019）0+4sin60°﹣+|﹣3|‎ ‎18．（8分）解二元一次方组：‎ ‎19．（10分）已知：如图，在▱ABCD中，AE⊥BC，CF⊥AD，E，F分别为垂足．‎ ‎（1）求证：△ABE≌△CDF；‎ ‎（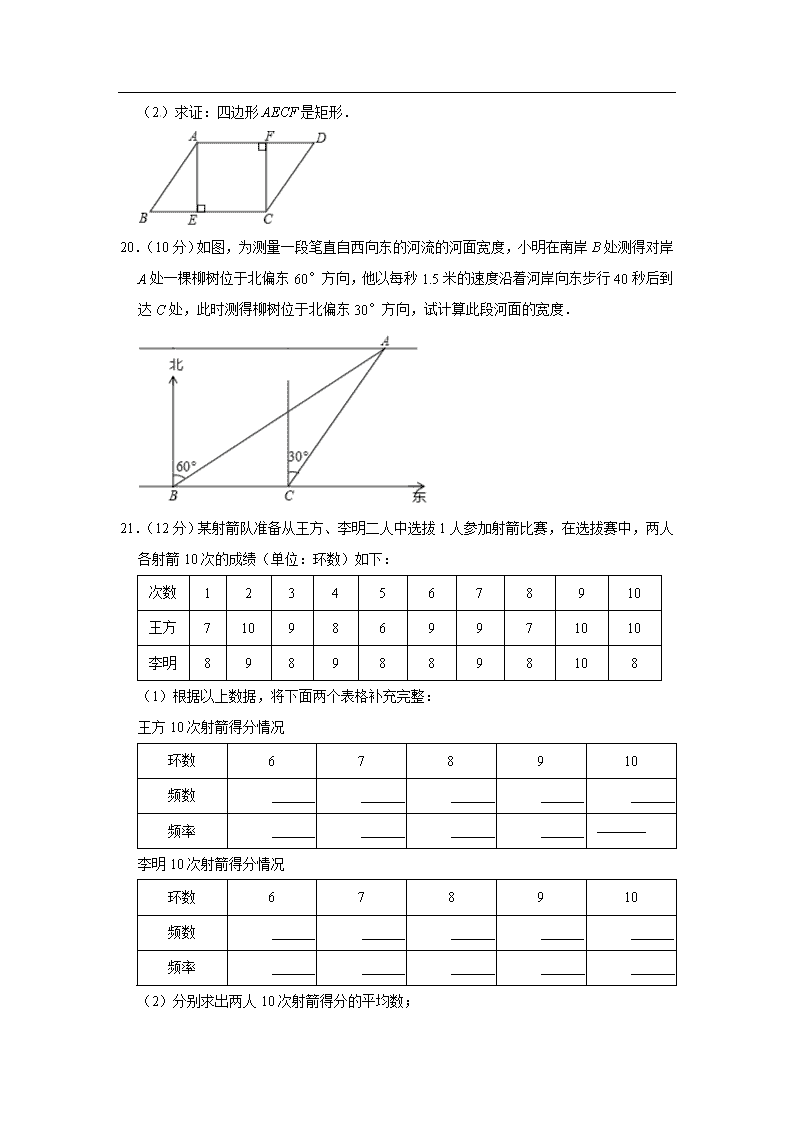2）求证：四边形AECF是矩形．‎ ‎20．（10分）如图，为测量一段笔直自西向东的河流的河面宽度，小明在南岸B处测得对岸A处一棵柳树位于北偏东60°方向，他以每秒1.5米的速度沿着河岸向东步行40秒后到达C处，此时测得柳树位于北偏东30°方向，试计算此段河面的宽度．‎ ‎21．（12分）某射箭队准备从王方、李明二人中选拔1人参加射箭比赛，在选拔赛中，两人各射箭10次的成绩（单位：环数）如下：‎ 次数 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 王方 ‎7‎ ‎10‎ ‎9‎ ‎8‎ ‎6‎ ‎9‎ ‎9‎ ‎7‎ ‎10‎ ‎10‎ 李明 ‎8‎ ‎9‎ ‎8‎ ‎9‎ ‎8‎ ‎8‎ ‎9‎ ‎8‎ ‎10‎ ‎8‎ ‎（1）根据以上数据，将下面两个表格补充完整：‎ 王方10次射箭得分情况 ‎ 环数 ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 频数 ‎　 　‎ ‎　 　‎ ‎　 　‎ ‎　 　‎ ‎　 　‎ 频率 ‎　 　‎ ‎　 　‎ ‎　 　‎ ‎　 　‎ ‎　 　[来源:Zxxk.Com]‎ 李明10次射箭得分情况 ‎ 环数 ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 频数 ‎　 　‎ ‎　 　‎ ‎　 　‎ ‎　 　‎ ‎　 　‎ 频率 ‎　 　‎ ‎　 　‎ ‎　 　‎ ‎　 　‎ ‎　 　‎ ‎（2）分别求出两人10次射箭得分的平均数；‎ ‎（3）从两人成绩的稳定性角度分析，应选派谁参加比赛合适．‎ ‎22．（12分）如图，A、B、C、D、E是⊙O上的5等分点，连接AC、CE、EB、BD、DA，得到一个五角星图形和五边形MNFGH．‎ ‎（1）计算∠CAD的度数；‎ ‎（2）连接AE，证明：AE＝ME；‎ ‎（3）求证：ME2＝BM•BE．‎ ‎[来源:Z.xx.k.Com][来源:学#科#网]‎ ‎23．（14分）如图，在直角坐标系中有Rt△AOB，O为坐标原点，OB＝1，tan∠ABO＝3，将此三角形绕原点O顺时针旋转90°，得到Rt△COD，二次函数y＝﹣x2+bx+c的图象刚好经过A，B，C三点．‎ ‎（1）求二次函数的解析式及顶点P的坐标；‎ ‎（2）过定点Q的直线l：y＝kx﹣k+3与二次函数图象相交于M，N两点．‎ ‎①若S△PMN＝2，求k的值；‎ ‎②证明：无论k为何值，△PMN恒为直角三角形；‎ ‎③当直线l绕着定点Q旋转时，△PMN外接圆圆心在一条抛物线上运动，直接写出该抛物线的表达式．‎ ‎2019年湖南省怀化市中考数学试卷 参考答案与试题解析 一、选择题（每小题4分，共40分；每小題的四个选项中只有一项是正确的，请将正确选项的代号填涂在答题卡的相应位置上）‎ ‎1．（4分）下列实数中，哪个数是负数（　　）‎ A．0 B．3 C． D．﹣1‎ ‎【分析】根据小于零的数是负数，可得答案．‎ ‎【解答】解：A、0既不是正数也不是负数，故A错误；‎ B、3是正实数，故B错误；‎ C、是正实数，故C错误；‎ D、﹣1是负实数，故D正确；‎ 故选：D．‎ ‎【点评】本题考查了实数，小于零的数是负数，属于基础题型．‎ ‎2．（4分）单项式﹣5ab的系数是（　　）‎ A．5 B．﹣5 C．2 D．﹣2‎ ‎【分析】根据单项式系数的定义来选择，单项式中数字因数叫做单项式的系数，单项式中，所有字母的指数和叫做这个单项式的次数，可得答案 ‎【解答】解：单项式﹣5ab的系数是﹣5，‎ 故选：B．‎ ‎【点评】本题考查单项式，注意单项式中数字因数叫做单项式的系数，所有字母的指数和叫做这个单项式的次数．‎ ‎3．（4分）怀化位于湖南西南部，区域面积约为27600平方公里，将27600用科学记数法表示为（　　）‎ A．27.6×103 B．2.76×103 C．2.76×104 D．2.76×105‎ ‎【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．‎ ‎【解答】解：将27600用科学记数法表示为：2.76×105．‎ 故选：D．‎ ‎【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．‎ ‎4．（4分）抽样调查某班10名同学身高（单位：厘米）如下：160，152，165，152，160，160，170，160，165，159．则这组数据的众数是（　　）‎ A．152 B．160 C．165 D．170‎ ‎【分析】根据众数定义：一组数据中出现次数最多的数据叫众数，可知160出现的次数最多．‎ ‎【解答】解：数据160出现了4次为最多，‎ 故众数是160，‎ 故选：B．‎ ‎【点评】此题主要考查了众数，关键是把握众数定义，难度较小．‎ ‎5．（4分）与30°的角互为余角的角的度数是（　　）‎ A．30° B．60° C．70° D．90°‎ ‎【分析】直接利用互为余角的定义分析得出答案．‎ ‎【解答】解：与30°的角互为余角的角的度数是：60°．‎ 故选：B．‎ ‎【点评】此题主要考查了互为余角的定义，正确把握互为余角的定义是解题关键．‎ ‎6．（4分）一元一次方程x﹣2＝0的解是（　　）‎ A．x＝2 B．x＝﹣2 C．x＝0 D．x＝1‎ ‎【分析】直接利用一元一次方程的解法得出答案．‎ ‎【解答】解：x﹣2＝0，‎ 解得：x＝2．‎ 故选：A．‎ ‎【点评】此题主要考查了一元一次方程的解法，正确掌握基本解题方法是解题关键．‎ ‎7．（4分）怀化是一个多民族聚居的地区，民俗文化丰富多彩．下面是几幅具有浓厚民族特色的图案，其中既是轴对称图形又是中心对称图形的是（　　）‎ A． B． ‎ C． D．‎ ‎【分析】直接利用轴对称图形和中心对称图形的概念求解．‎ ‎【解答】解：A、是轴对称图形，不是中心对称图形，故此选项错误；‎ B、是轴对称图形，不是中心对称图形，故此选项错误；[来源:学科网]‎ C、既是中心对称图形也是轴对称图形，故此选项正确；‎ D、是轴对称图形，但不是中心对称图形，故此选项错误．‎ 故选：C．‎ ‎【点评】此题主要考查了中心对称与轴对称的概念：轴对称的关键是寻找对称轴，两边图象折叠后可重合，中心对称是要寻找对称中心，旋转180°后与原图重合．‎ ‎8．（4分）已知∠α为锐角，且sinα＝，则∠α＝（　　）‎ A．30° B．45° C．60° D．90°‎ ‎【分析】根据特殊角的三角函数值解答．‎ ‎【解答】解：∵∠α为锐角，且sinα＝，‎ ‎∴∠α＝30°．‎ 故选：A．‎ ‎【点评】此题考查的是特殊角的三角函数值，属较简单题目．‎ ‎9．（4分）一元二次方程x2+2x+1＝0的解是（　　）‎ A．x1＝1，x2＝﹣1 B．x1＝x2＝1 C．x1＝x2＝﹣1 D．x1＝﹣1，x2＝2‎ ‎【分析】利用完全平方公式变形，从而得出方程的解．‎ ‎【解答】解：∵x2+2x+1＝0，‎ ‎∴（x+1）2＝0，‎ 则x+1＝0，‎ 解得x1＝x2＝﹣1，‎ 故选：C．‎ ‎【点评】本题主要考查解一元二次方程的能力，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．‎ ‎10．（4分）为了落实精准扶贫政策，某单位针对某山区贫困村的实际情况，特向该村提供优质种羊若干只．在准备配发的过程中发现：公羊刚好每户1只；若每户发放母羊5只，则多出17只母羊，若每户发放母羊7只，则有一户可分得母羊但不足3只．这批种羊共（　　）只．‎ A．55 B．72 C．83 D．89‎ ‎【分析】设该村共有x户，则母羊共有（5x+17）只，根据“每户发放母羊7只时有一户可分得母羊但不足3只”列出关于x的不等式组，解之求得整数x的值，再进一步计算可得．‎ ‎【解答】解：设该村共有x户，则母羊共有（5x+17）只，‎ 由题意知，‎ 解得：＜x＜12，‎ ‎∵x为整数，‎ ‎∴x＝11，‎ 则这批种羊共有11+5×11+17＝83（只），‎ 故选：C．‎ ‎【点评】本题主要考查一元一次不等式组的应用，解题的关键是理解题意找到题目蕴含的不等关系，并据此得出不等式组．‎ 二、填空题（每小题4分，共24分；请将答案直接填写在答题卡的相应位置上）‎ ‎11．（4分）合并同类项：4a2+6a2﹣a2＝　9a2　．‎ ‎【分析】根据合并同类项法则计算可得．‎ ‎【解答】解：原式＝（4+6﹣1）a2＝9a2，‎ 故答案为：9a2．‎ ‎【点评】本题考查合并同类项，合并同类项时要注意以下三点：‎ ‎①‎ 要掌握同类项的概念，会辨别同类项，并准确地掌握判断同类项的两条标准：带有相同系数的代数项；字母和字母指数；‎ ‎②明确合并同类项的含义是把多项式中的同类项合并成一项，经过合并同类项，式的项数会减少，达到化简多项式的目的；‎ ‎③“合并”是指同类项的系数的相加，并把得到的结果作为新的系数，要保持同类项的字母和字母的指数不变．‎ ‎12．（4分）因式分解：a2﹣b2＝　（a+b）（a﹣b）　．‎ ‎【分析】利用平方差公式直接分解即可求得答案．‎ ‎【解答】解：a2﹣b2＝（a+b）（a﹣b）．‎ 故答案为：（a+b）（a﹣b）．‎ ‎【点评】此题考查了平方差公式的应用．解题的关键是熟记公式．‎ ‎13．（4分）计算：﹣＝　1　．‎ ‎【分析】由于两分式的分母相同，分子不同，故根据同分母的分式相加减的法则进行计算即可．‎ ‎【解答】解：原式＝‎ ‎＝1．‎ 故答案为：1．‎ ‎【点评】本题考查的是分式的加减法，即同分母的分式想加减，分母不变，把分子相加减．‎ ‎14．（4分）若等腰三角形的一个底角为72°，则这个等腰三角形的顶角为　36°　．‎ ‎【分析】根据等腰三角形的性质和三角形的内角和即可得到结论．‎ ‎【解答】解：∵等腰三角形的一个底角为72°，‎ ‎∴等腰三角形的顶角＝180°﹣72°﹣72°＝36°，‎ 故答案为：36°．‎ ‎【点评】本题考查了等腰三角形的性质，熟练掌握等腰三角形的性质是解题的关键．‎ ‎15．（4分）当a＝﹣1，b＝3时，代数式2a﹣b的值等于　﹣5　．‎ ‎【分析】把a、b的值代入代数式，即可求出答案即可．‎ ‎【解答】解：当a＝﹣1，b＝3时，2a﹣b＝2×（﹣1）﹣3＝﹣5，‎ 故答案为：﹣5．‎ ‎【点评】‎ 本题考查了求代数式的值的应用，能正确进行有理数的混合运算是解此题的关键．‎ ‎16．（4分）探索与发现：下面是用分数（数字表示面积）砌成的“分数墙”，则整面“分数墙”的总面积是　n﹣1　．‎ ‎【分析】由题意“分数墙”的总面积＝2×+3×+4×+…+n×＝n﹣1．‎ ‎【解答】解：由题意“分数墙”的总面积＝2×+3×+4×+…+n×＝n﹣1，‎ 故答案为n﹣1．‎ ‎【点评】本题考查规律型问题，有理数的混合运算等知识，解题的关键是理解题意，灵活运用所学知识解决问题．‎ 三、解答题（本大题共7小题，共86分）‎ ‎17．（8分）计算：（π﹣2019）0+4sin60°﹣+|﹣3|‎ ‎【分析】先计算零指数幂、代入三角函数值、化简二次根式、取绝对值符号，再计算乘法，最后计算加减可得．‎ ‎【解答】解：原式＝1+4×﹣2+3‎ ‎＝1+2﹣2+3‎ ‎＝4．‎ ‎【点评】本题主要考查实数的运算，解题的关键是掌握零指数幂的规定、熟记特殊锐角三角函数值及二次根式与绝对值的性质．‎ ‎18．（8分）解二元一次方组：‎ ‎【分析】直接利用加减消元法进而解方程组即可．‎ ‎【解答】解：，‎ ‎①+②得：‎ ‎2x＝8，‎ 解得：x＝4，‎ 则4﹣3y＝1，‎ 解得：y＝1，‎ 故方程组的解为：．‎ ‎【点评】此题主要考查了解二元一次方程组，正确掌握解题方法是解题关键．‎ ‎19．（10分）已知：如图，在▱ABCD中，AE⊥BC，CF⊥AD，E，F分别为垂足．‎ ‎（1）求证：△ABE≌△CDF；‎ ‎（2）求证：四边形AECF是矩形．‎ ‎【分析】（1）由平行四边形的性质得出∠B＝∠D，AB＝CD，AD∥BC，由已知得出∠AEB＝∠AEC＝∠CFD＝∠AFC＝90°，由AAS证明△ABE≌△CDF即可；‎ ‎（2）证出∠EAF＝∠AEC＝∠AFC＝90°，即可得出结论．‎ ‎【解答】（1）证明：∵四边形ABCD是平行四边形，‎ ‎∴∠B＝∠D，AB＝CD，AD∥BC，‎ ‎∵AE⊥BC，CF⊥AD，‎ ‎∴∠AEB＝∠AEC＝∠CFD＝∠AFC＝90°，‎ 在△ABE和△CDF中，，‎ ‎∴△ABE≌△CDF（AAS）；‎ ‎（2）证明：∵AD∥BC，‎ ‎∴∠EAF＝∠AEB＝90°，‎ ‎∴∠EAF＝∠AEC＝∠AFC＝90°，‎ ‎∴四边形AECF是矩形．‎ ‎【点评】本题考查了矩形的判定、平行四边形的性质、全等三角形的判定与性质；熟练掌握平行四边形的性质和矩形的判定是解题的关键．‎ ‎20．（10分）如图，为测量一段笔直自西向东的河流的河面宽度，小明在南岸B处测得对岸A处一棵柳树位于北偏东60°方向，他以每秒1.5米的速度沿着河岸向东步行40秒后到达C处，此时测得柳树位于北偏东30°方向，试计算此段河面的宽度．‎ ‎【分析】如图，作AD⊥于BC于D．由题意得到BC＝1.5×40＝60米，∠ABD＝30°，∠ACD＝60°，根据三角形的外角的性质得到∠BAC＝∠ACD﹣∠ABC＝30°，求得∠ABC＝∠BAC，得到BC＝AC＝60米．在Rt△ACD中，根据三角函数的定义即可得到结论．‎ ‎【解答】解：如图，作AD⊥于BC于D．‎ 由题意可知：BC＝1.5×40＝60米，∠ABD＝30°，∠ACD＝60°，‎ ‎∴∠BAC＝∠ACD﹣∠ABC＝30°，‎ ‎∴∠ABC＝∠BAC，[来源:Zxxk.Com]‎ ‎∴BC＝AC＝60米．‎ 在Rt△ACD中，AD＝AC•sin60°＝60×＝30（米）．‎ 答：这条河的宽度为30米．‎ ‎【点评】此题主要考查了解直角三角形﹣方向角问题，解题时首先正确理解题意，然后作出辅助线构造直角三角形解决问题．‎ ‎21．（12分）某射箭队准备从王方、李明二人中选拔1人参加射箭比赛，在选拔赛中，两人各射箭10次的成绩（单位：环数）如下：‎ 次数 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 王方 ‎7‎ ‎10‎ ‎9‎ ‎8‎ ‎6‎ ‎9‎ ‎9‎ ‎7‎ ‎10‎ ‎10‎ 李明 ‎8‎ ‎9‎ ‎8‎ ‎9‎ ‎8‎ ‎8‎ ‎9‎ ‎8‎ ‎10‎ ‎8‎ ‎（1）根据以上数据，将下面两个表格补充完整：‎ 王方10次射箭得分情况 ‎ 环数 ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 频数 ‎　1　‎ ‎　2　‎ ‎　1　‎ ‎　3　‎ ‎　3　‎ 频率 ‎　0.1　‎ ‎　0.2　‎ ‎　0.1　‎ ‎　0.3　‎ ‎　0.3　‎ 李明10次射箭得分情况 ‎ 环数 ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 频数 ‎　0　‎ ‎　0　‎ ‎　6　‎ ‎　3　‎ ‎　1　‎ 频率 ‎　0　‎ ‎　0　‎ ‎　0.6　‎ ‎　0.3　‎ ‎　0.1　‎ ‎（2）分别求出两人10次射箭得分的平均数；‎ ‎（3）从两人成绩的稳定性角度分析，应选派谁参加比赛合适．‎ ‎【分析】（1）根据各组的频数除以10即可得到结论；‎ ‎（2）根据加权平均数的定义即可得到结论；‎ ‎（3）根据方差公式即可得到结论．‎ ‎【解答】解：（1）‎ 环数 ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 频数 ‎1‎ ‎2‎ ‎1‎ ‎3‎ ‎3‎ 频率 ‎0.1‎ ‎0.2‎ ‎0.1‎ ‎0.3‎ ‎0.3‎ 李明10次射箭得分情况 ‎ 环数 ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 频数 ‎0‎ ‎0‎ ‎6‎ ‎3‎ ‎1‎ 频率 ‎0‎ ‎0‎ ‎0.6‎ ‎0.3‎ ‎0.1‎ ‎（2）王方的平均数＝（6+14+8+27+30）＝8.5；李明的平均数＝（48+27+10）＝8.5；‎ ‎（3）∵S＝[（6﹣8.5）2+2（7﹣8.5）2+（8﹣8.5）2+3（9﹣8.5）2+3（10﹣8.5）2]＝1.85；‎ S＝[6（8﹣8.5）2+3（9﹣8.5）2+（10﹣8.5）2＝0.35；‎ ‎∵S＞S，‎ ‎∴应选派李明参加比赛合适．‎ ‎【点评】本题考查方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．‎ ‎22．（12分）如图，A、B、C、D、E是⊙O上的5等分点，连接AC、CE、EB、BD、DA，得到一个五角星图形和五边形MNFGH．‎ ‎（1）计算∠CAD的度数；‎ ‎（2）连接AE，证明：AE＝ME；‎ ‎（3）求证：ME2＝BM•BE．‎ ‎【分析】（1）由题意可得∠COD＝70°，由圆周角的定理可得∠CAD＝36°；‎ ‎（2）由圆周角的定理可得∠CAD＝∠DAE＝∠AEB＝36°，可求∠AME＝∠CAE＝72°，可得AE＝ME；‎ ‎（3）通过证明△AEN∽△BEA，可得，可得ME2＝BE•NE，通过证明BM＝NE，即可得结论．‎ ‎【解答】解：（1）∵A、B、C、D、E是⊙O上的5等分点，‎ ‎∴的度数＝＝72°‎ ‎∴∠COD＝70°‎ ‎∵∠COD＝2∠CAD ‎∴∠CAD＝36°‎ ‎（2）连接AE ‎∵A、B、C、D、E是⊙O上的5等分点，‎ ‎∴‎ ‎∴∠CAD＝∠DAE＝∠AEB＝36°‎ ‎∴∠CAE＝72°，且∠AEB＝36°‎ ‎∴∠AME＝72°‎ ‎∴∠AME＝∠CAE ‎∴AE＝ME ‎（3）连接AB ‎∵‎ ‎∴∠ABE＝∠DAE，且∠AEB＝∠AEB ‎∴△AEN∽△BEA ‎∴‎ ‎∴AE2＝BE•NE，且AE＝ME ‎∴ME2＝BE•NE ‎∵‎ ‎∴AE＝AB，∠CAB＝∠CAD＝∠DAE＝∠BEA＝∠ABE＝36°‎ ‎∴∠BAD＝∠BNA＝72°‎ ‎∴BA＝BN，且AE＝ME ‎∴BN＝ME ‎∴BM＝NE ‎∴ME2＝BE•NE＝BM•BE ‎【点评】本题是圆的综合题，考查了圆的有关知识，相似三角形的性质和判定，证明△AEN∽△BEA是本题的关键．‎ ‎23．（14分）如图，在直角坐标系中有Rt△AOB，O为坐标原点，OB＝1，tan∠ABO＝3，将此三角形绕原点O顺时针旋转90°，得到Rt△COD，二次函数y＝﹣x2+bx+c的图象刚好经过A，B，C三点．‎ ‎（1）求二次函数的解析式及顶点P的坐标；‎ ‎（2）过定点Q的直线l：y＝kx﹣k+3与二次函数图象相交于M，N两点．‎ ‎①若S△PMN＝2，求k的值；‎ ‎②证明：无论k为何值，△PMN恒为直角三角形；‎ ‎③当直线l绕着定点Q旋转时，△PMN外接圆圆心在一条抛物线上运动，直接写出该抛物线的表达式．‎ ‎【分析】（1）求出点A、B、C的坐标分别为（0，3）、（﹣1，0）、（3，0），即可求解；‎ ‎（2）①S△PMN＝PQ×（x2﹣x1），则x2﹣x1＝4，即可求解；②k1k2＝＝＝﹣1，即可求解；③取MN的中点H，则点H是△PMN外接圆圆心，即可求解．‎ ‎【解答】解：（1）OB＝1，tan∠ABO＝3，则OA＝3，OC＝3，‎ 即点A、B、C的坐标分别为（0，3）、（﹣1，0）、（3，0），‎ 则二次函数表达式为：y＝a（x﹣3）（x+1）＝a（x2﹣2x﹣3），‎ 即：﹣3a＝3，解得：a＝﹣1，‎ 故函数表达式为：y＝﹣x2+2x+3，‎ 点P（1，4）；‎ ‎（2）将二次函数与直线l的表达式联立并整理得：‎ x2﹣（2﹣k）x﹣k＝0，‎ 设点M、N的坐标为（x1，y1）、（x2，y2），‎ 则x1+x2＝2﹣k，x1x2＝﹣k，‎ 则：y1+y2＝k（x1+x2）﹣2k+6＝6﹣k2，‎ 同理：y1y2＝9﹣4k2，‎ ‎①y＝kx﹣k+3，当x＝1时，y＝3，即点Q（1，3），‎ S△PMN＝2＝PQ×（x2﹣x1），则x2﹣x1＝4，‎ ‎|x2﹣x1|＝，‎ 解得：k＝±2；‎ ‎②点M、N的坐标为（x1，y1）、（x2，y2）、点P（1，4），‎ 则直线PM表达式中的k1值为：，直线PN表达式中的k2值为：，‎ 为：k1k2＝＝＝﹣1，‎ 故PM⊥PN，‎ 即：△PMN恒为直角三角形；‎ ‎③取MN的中点H，则点H是△PMN外接圆圆心，‎ 设点H坐标为（x，y），‎ 则x＝＝1﹣k，‎ y＝（y1+y2）＝（6﹣k2），‎ 整理得：y＝﹣2x2+4x+1，‎ 即：该抛物线的表达式为：y＝﹣2x2+4x+1．‎ ‎【点评】本题考查的是二次函数综合运用，涉及到一次函数、圆的基本知识等，其中，用韦达定理处理复杂数据，是本题解题的关键．‎