2009年北京市宣武区中考数学二模试卷 12页

‎13 2009年北京市宣武区中考数学二模试卷 第Ⅰ卷(机读卷 共32分)‎ 一、选择题(共8个小题，每小题4分，共32分)‎ 下列各题均有四个选项，其中只有一个是符合题意的．用铅笔把“机读答题卡”上对应题目答案的相应字母处涂黑．‎ ‎1．－3的立方是( )‎ A．－27 B．－‎9 ‎C．9 D．27‎ ‎2．据统计，2008年中国某小商品批发市场全年成交额约为348.4亿元．近似数348.4亿元的有效数字的个数是( )‎ A．6个 B．5个 C．4个 D．11个 ‎3．正方形网格中，∠AOB如图放置，则cos∠AOB的值为( )‎ 第3题图 A． B．‎2 ‎C． D．‎ ‎4．已知甲、乙两组数据的平均数分别是甲＝80，乙＝90，方差分别是＝10，＝5，比较这两组数据，下列说法正确的是( )‎ A．乙组数据的波动较小 B．乙组数据较好 C．甲组数据的极差较大 D．甲组数据较好 ‎5．若等腰三角形的两条边长分别为‎3cm和‎6cm，则它的周长为( )‎ A．‎9cm B．‎12cm C．‎15cm D．‎12cm或‎15cm ‎6．下列四个三角形中，与左图中的三角形相似的是( )‎ 第6题图 ‎7．函数y＝6－x与函数的图象交于A、B两点，设点A的坐标为(x1，y1)，则边长分别为x1、y1的矩形面积和周长分别为( )‎ A．4，12 B．4，‎6 ‎C．8，12 D．8，6‎ ‎8．如图，在Rt△ABC中，AB＝AC，D、E是斜边BC上两点，且∠DAE＝45°，将△ADC绕点A顺时针旋转90°后，得到△AFB，连结EF，下列结论：‎ ‎①△AED≌△AEF； ②△ABE～△ACD；‎ ‎③BE＋DC＝DE； ④BE2＋DC2＝DE2．‎ 其中一定正确的是( )‎ A．②④ B．①③ C．②③ D．①④‎ 第8题图 第Ⅱ卷(非机读卷 共88分)‎ 二、填空题(共4道小题，每小题4分，共16分)‎ ‎9．分解因式y3－4y2＋4y＝________．‎ ‎10．函数中，自变量x的取值范围是________．‎ ‎11．一个口袋里有4个白球，5个红球，6个黄球，每个球除颜色外都相同，搅匀后随机从袋中摸出一个球，这个球是白球的概率是________．‎ ‎12．如图，OA＝OB，A点坐标是(－,0)，OB与x轴正方向夹角为45°，则B点坐标是________．AB与y轴交于点C，若以OC为轴，将△OBC沿OC翻折，B点落在第二象限内B’处，则BB’的长度为________．‎ 第12题图 三、解答题(共13道小题，共72分)‎ ‎13．(本小题满分5分)‎ 计算：．‎ ‎14．(本小题满分5分)‎ 解方程：．‎ ‎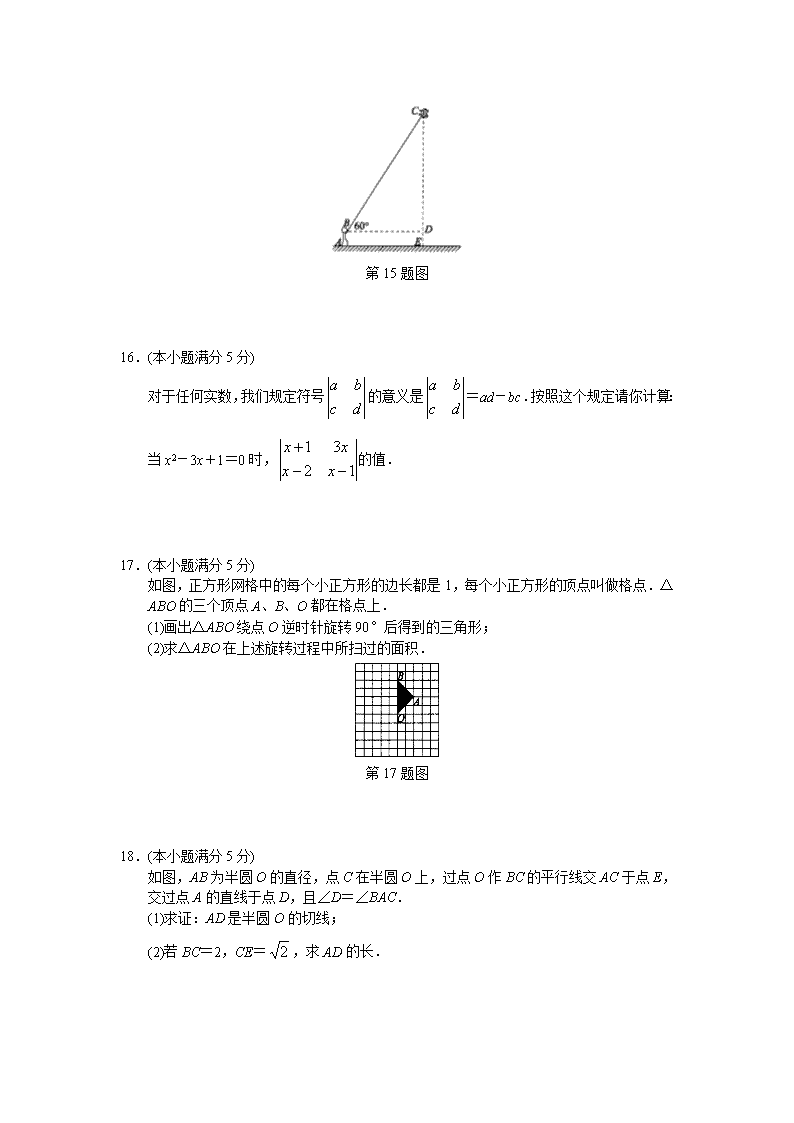15．(本小题满分5分)‎ 小明站在A处放风筝，风筝飞到C处时的线长为‎20m，这时测得∠CBD＝60°，若牵引底端B离地面‎1.5m，求此时风筝离地面高度．(计算结果精确到‎0.1m，≈1.732)‎ 第15题图 ‎16．(本小题满分5分)‎ 对于任何实数，我们规定符号的意义是＝ad－bc．按照这个规定请你计算：当x2－3x＋1＝0时，的值．‎ ‎17．(本小题满分5分)‎ 如图，正方形网格中的每个小正方形的边长都是1，每个小正方形的顶点叫做格点．△ABO的三个顶点A、B、O都在格点上．‎ ‎(1)画出△ABO绕点O逆时针旋转90°后得到的三角形；‎ ‎(2)求△ABO在上述旋转过程中所扫过的面积．‎ 第17题图 ‎18．(本小题满分5分)‎ 如图，AB为半圆O的直径，点C在半圆O上，过点O作BC的平行线交AC于点E，交过点A的直线于点D，且∠D＝∠BAC．‎ ‎(1)求证：AD是半圆O的切线；‎ ‎(2)若BC＝2，CE＝，求AD的长．‎ 第18题图 ‎19．(本小题满分5分)‎ 如图，在△ABC中，∠CAB、∠ABC的平分线交于点D，DE∥AC交BC于点E，DF∥BC交AC于点F．‎ 求证：四边形DECF为菱形．‎ 第19题图 ‎20．(本小题满分5分)‎ 某校为了了解九年级学生体育测试成绩情况，以九年级(1)班学生的体育测试成绩为样本，按A、B、C、D四个等级进行统计，并将统计结果绘制成以下两幅统计图，请你结合图中所给信息解答下列问题：(A级：90分～100分；B级：75分～89分；C级：60分～74分；D级：60分以下)‎ ‎(1)D级学生的人数占全班人数的百分比为________；‎ ‎(2)扇形统计图中C级所在扇形圆心角度数为________；‎ ‎(3)该班学生体育测试成绩的中位数落在等级________内；‎ ‎(4)若该校九年级学生共有500人，请你估计这次考试中A级和B级的学生共有多少人．‎ 第20题图 ‎21．(本小题满分5分)‎ 一辆经营长途运输的货车在高速公路上的A处加满油后匀速行驶，下表记录的是货车一次加满油后油箱内余油量y(L)与行驶时间x(h)之间的关系：‎ 行驶时间x(h)‎ ‎0‎ ‎1‎ ‎2‎ ‎2.5‎ 余油量y(L)‎ ‎100‎ ‎80‎ ‎60‎ ‎50‎ ‎(1)请你认真分析上表中所给的数据，用你学过的一次函数、反比例函数和二次函数中的一种来表示y与x之间的变化规律，说明选择这种函数的理由，并求出它的函数表达式；(不要求写出自变量的取值范围)‎ ‎(2)按照(1)中的变化规律，货车从A处出发行驶4.2 h到达B处，求此时油箱内余油多少升．‎ ‎22．(本小题满分5分)‎ 定义[p，q]为一次函数y＝px＋q的特征数．‎ ‎(1)若特征数是[2，k－2]的一次函数为正比例函数，求k的值；‎ ‎(2)设点A、B分别为抛物线y＝(x＋m)(x－2)与x轴、y轴的交点，其中m＞0，且△OAB的面积为4，O为坐标原点，求图象过A、B两点的一次函数的特征数．‎ ‎23．(本小题满分7分)‎ 已知二次函数y＝ax2＋4ax＋‎4a－1的图象是C1．‎ ‎(1)求C1关于点R(1，0)中心对称的图象C2的函数解析式；‎ ‎(2)在(1)的条件下，设抛物线C1、C2与y轴的交点分别为A、B，当AB＝18时，求a的值．‎ ‎24．(本小题满分7分)‎ ‎(1)如图①，△ABC是⊙O的内接正三角形，点P为上一动点，‎ 求证：PA＝PB＋PC；‎ ‎(2)如图②，四边形ABCD是⊙O的内接正方形，点P为上一动点，求证：‎ PA＝PC＋PB；‎ ‎(3)如图③，六边形ABCDEF是⊙O的内接正六边形，点P为上一动点，请探究PA、PB、PC三者之间有何数量关系，并给予证明．‎ 第24题图 ‎25．(本小题满分8分)‎ 如图，菱形OABC的顶点O在坐标原点，顶点B在x轴的正半轴上，OA边在直线y＝上，AB边在直线y＝－x＋2上．‎ ‎(1)直接写出O、A、B、C的坐标．‎ ‎(2)在OB上有一动点P，以O为圆心、OP为半径画弧，分别交边OA、OC于M、N(M、N可以与A、C重合)，作⊙Q与边AB、BC和都相切，⊙Q分别与边AB、BC相切于点D、E，设⊙Q的半径为r，OP的长为y，求y与r之间的函数关系式，并写出自变量r的取值范围．‎ ‎(3)以O为圆心、OA为半径作扇形OAC，请问在菱形OABC中，除去扇形OAC后剩余部分内，是否可以截下一个圆，使得它与扇形OAC刚好围成一个圆锥?若可以，求出这个圆的面积；若不可以，说明理由．‎ 第25题图 答 案 ‎13．2009年北京市宣武区中考数学二模试卷 一、选择题 ‎1．A 2．C 3．D 4．A 5．C 6．B 7．A 8．D 二、填空题 ‎9．y(y－2)2 10．x≠3 11． 12．(1，1) 2‎ 三、解答题 ‎13．解：原式＝4－3＋1＋3‎ ‎＝5．‎ ‎14．解：方程两边同乘(x－1)(x＋1)，得 ‎2(x－1)－x＝0．‎ 解这个方程，得 x＝2．‎ 检验：当x＝2时，(x－1)(x＋1)≠0．‎ 所以x＝2是原方程的解．‎ ‎15．解：在Rt△BCD中，CD＝BC×sin60°．‎ 又∵DE＝AB＝1.5，‎ ‎∴CE＝CD＋DE＝10＋1.5≈17.32＋1.5≈‎18.8m．‎ 答：此时风筝离地面的高度约是‎18.8m．‎ ‎16．解：‎ ‎＝x2－1－3x2＋6x ‎＝－2x2＋6x－1．‎ ‎∵x2－3x＋1＝0，‎ ‎∴x2－3x＝－1．‎ ‎∴原式＝－2(x2－3x)－1＝2－1＝1．‎ ‎17．解：(1)如图．‎ 第17题答图 ‎(2)△ABC所扫过的面积是：‎ ‎＝4p ＋4．‎ ‎18．(1)证明：∵AB为半圆O的直径，‎ ‎∴∠BCA＝90°．‎ 又∵BC∥OD，∴OE⊥AC，‎ ‎∴∠D＋∠DAE＝90°．‎ ‎∵∠D＝∠BAC，∴∠BAC＋∠DAE＝90°．‎ ‎∴半径OA⊥AD于点A，∴AD是半圆O的切线．‎ ‎(2)解：∵在⊙O中，OE⊥AC于E，∴AC＝2CE＝2．‎ 在Rt△ABC中，，．‎ ‎∵∠D＝∠BAC，∠OAD＝∠C，‎ ‎∴△DOA∽△ABC，‎ ‎，‎ ‎，‎ ‎∴AD＝．‎ ‎19．证明：方法一：连结CD．‎ ‎①‎ ‎∵DE∥AC，DF∥BC，‎ ‎∴四边形DECF为平行四边形，‎ ‎∵∠CAB、∠ABC平分线交于点D，‎ ‎∴点D是△ABC的内心，‎ ‎∴CD平分∠ACB，即∠FCD＝∠ECD．‎ ‎∵FD∥BC，∴∠FDC＝∠ECD，∴∠FCD＝∠FDC．‎ ‎∴FC＝FD，‎ ‎∴□DECF为菱形．‎ 方法二：过D分别作DG⊥AB于G，DH⊥BC于H，DI⊥AC于I．‎ ‎∵AD、BD分别平分∠CAB、∠ABC，‎ ‎∴DI＝DG，DG＝DH．‎ ‎∴DH＝DI．‎ ‎∵DE∥AC，DF∥BC，‎ ‎∴四边形DECF为平行四边形，‎ ‎∴S□DECF＝CE·DH＝CF·DI,‎ ‎∴CE＝CF．‎ ‎∴□DECF为菱形．‎ ‎②‎ 第19题答图 ‎20．解：(1)4%．(2)72°．(3)B级 ‎(4)由题意可知，A级和B级学生的人数和占总人数的76％，‎ ‎∴500×76％＝380．‎ ‎∴估计这次考试中A级和B级的学生共有380人．‎ ‎21.解：(1)设y与x之间的关系为一次函数，其函数表达式为y＝kx＋b．‎ 将(0，100)，(1，80)代入上式，得 解得 ‎∴y＝－20x＋100．‎ 验证：当x＝2时，y＝－20×2＋100＝60，符合一次函数y＝－20x＋100；‎ 当x＝2.5时，y＝－20×2.5＋100＝50，也符合一次函数y＝－20x＋100．‎ ‎∴可用一次函数y＝－20x＋100表示其变化规律，而不用反比例函数、二次函数表示其变化规律．‎ ‎∴y与x之间的关系是一次函数，其函数表达式为y＝－20x＋100．‎ ‎(2)当x＝4.2时，由y＝－20x＋100可得y＝16．‎ 即货车行驶到B处时油箱内余油‎16L．‎ ‎22．解：(1)特征数为[2，k－2]的一次函数为y＝2x＋k－2，‎ ‎∴k－2＝0，‎ ‎∴k＝2．‎ ‎(2)抛物线与x轴的交点为A1(－m,0)、A2(2，0)，与y轴的交点为B(0，－‎2m)．‎ 若，则，，(舍)；‎ 若，则，．‎ 综上，m＝2．‎ ‎∴抛物线为y＝(x＋2)(x－2)，它与x轴的交点为(－2，0)、(2，0)，与y轴的交点为(0，－4)，‎ ‎∴所求一次函数为y＝－2x－4或y＝2x－4，‎ ‎∴特征数为[－2，－4]或[2，－4]．‎ ‎23．解：(1)由y＝a(x＋2)2－1，可知抛物线C1的顶点为M(－2，－1)．由图知点M(－2，－1)关于点R(1，0)中心对称的点为N(4，1)，以N(4，1)为顶点，与抛物线C1关于点R(1，0)中心对称的图象C2也是抛物线，且C1与C2的开口方向相反，故抛物线C2的函数解析式为y＝－a(x－4)2＋1，‎ 即y＝－ax2＋8ax－‎16a＋1．‎ 第23题答图 ‎(2)令x＝0，得抛物线C1、C2与y轴的交点A、B的纵坐标分别为‎4a－1和－‎16a＋1，‎ ‎∴AB＝｜(‎4a－1)－(－‎16a＋1)｜＝｜‎20a－2｜．‎ ‎∴｜‎20a－2｜＝18．‎ 当时，有‎20a－2＝18，得a＝1；‎ 当时，有2－‎20a＝18，得．‎ ‎24．(1)证明：延长BP至E，使PE＝PC，连结CE．‎ ‎∵∠1＝∠2＝60°，∠3＝∠4＝60°，‎ ‎∴∠CPE＝60°，‎ ‎∴△PCE是等边三角形．‎ ‎∴CE＝PC，∠E＝∠3＝60°．‎ 又∵∠EBC＝∠PAC，‎ ‎∴△BEC≌△APC，∴PA＝BE＝PB＋PC．‎ ‎(2)证明：过点B作BE⊥PB交PA于E．‎ ‎∵∠1＋∠2＝∠2＋∠3＝90°，∴∠1＝∠3．‎ 又∵∠APB＝45°，‎ ‎∴BP＝BE，∴PE＝PB．‎ 又∵AB＝BC，∴△ABE≌△CBP，∴PC＝AE．‎ ‎∴PA＝AE＋PE＝PC＋PB．‎ ‎(3)PA＝PC＋PB．‎ 证明：在AP上截取AQ＝PC，连结BQ．‎ ‎∵∠BAP＝∠BCP，AB＝BC，‎ ‎∴△ABQ≌△CBP，∴BQ＝BP．‎ 又∵∠APB＝30°，∴PQ＝PB．‎ ‎∴PA＝PQ＋AQ＝PB＋PC．‎ ‎①‎ ‎②‎ ‎③‎ 第24题答图 ‎25．解：(1)O(0，0)，A(，1)，B(2，0)，C(，－1)．‎ ‎(2)连结QD、QE，则QD⊥AB，QE⊥BC．‎ ‎∵QD＝QE，∴点Q在∠ABC的平分线上．‎ 又∵OABC是菱形，∴点Q在OB上．‎ ‎∴⊙Q与弧MN相切于点P．‎ 在Rt△QDB中，∠QBD＝30°，‎ ‎∴QB＝2QD＝2r．∴y＋3r ‎＝2，y＝2－3r．‎ 其中．‎ ‎(3)可以．理由：弧AC的长为．‎ 设截下的⊙G符合条件，其半径为R，则2p R＝．．‎ 由(2)知，此时OA＝y＝2，则⊙Q的半径，‎ ‎∴能截下一个圆，使得它与扇形OAC刚好围成一个圆锥，‎ 此圆的面积为．‎ 第25题答图