2020-2021学年山西临汾九年级上数学月考试卷 10页

‎2020-2021学年山西临汾九年级上数学月考试卷 一、选择题 ‎ ‎ ‎1. 下列式子中，一定属于二次根式的是(        ) ‎ A.‎−5‎ B.x+2‎ C.‎3‎‎7‎ D.‎‎3‎ ‎ ‎ ‎2. 若一元二次方程x‎2‎‎+kx=0‎的一个根为x=−1‎，则k的值为(        ) ‎ A.‎−1‎ B.‎1‎ C.‎0‎ D.‎‎−2‎ ‎ ‎ ‎3. 下列运算中，正确的是(        ) ‎ A.‎9‎‎=±3‎ B.‎−3‎‎2‎‎=9‎ C.‎5‎‎2‎‎=5‎ D.‎‎−‎‎2‎‎2‎‎=−2‎ ‎ ‎ ‎4. 利用配方法解方程x‎2‎‎+2x=1‎时，方程可变形为(        ) ‎ A.x+1‎‎2‎‎=2‎ B.x−1‎‎2‎‎=2‎ C.x+1‎‎2‎‎=0‎ D.‎x−1‎‎2‎‎=0‎ ‎ ‎ ‎5. 下列二次根式能与‎3‎合并的是(         ) ‎ A.‎6‎ B.‎12‎ C.‎2‎‎3‎ D.‎‎24‎ ‎ ‎ ‎6. 一元二次方程x‎2‎‎+3x+4=0‎的根的情况是(        ) ‎ A.有两个不相等的实数根 B.没有实数根 C.有两个相等的实数根 D.有且只有一个实数根 ‎ ‎ ‎ ‎7. 如图所示的是一幅正方形风景画，现从大正方形风景画中剪去两个面积分别为‎4dm‎2‎和‎8dm‎2‎的小正方形风景画，则余下风景画的面积为(        ) ‎ A.‎4+6‎‎2‎dm‎2‎ B.‎8‎2‎dm‎2‎ C.‎4+12‎‎2‎dm‎2‎ D.‎‎6‎2‎dm‎2‎ ‎ ‎ ‎8. 我们规定：如果一个方程的两个实数根的比值与另一个方程的两个实数根的比值相等，我们称这两个方程为“像方程”，例如方程x−2‎x−8‎‎=0‎的两个实数根为‎2‎和‎8‎，方程x‎2‎‎−5x+4=0‎的两个实数根为‎1‎和‎4‎，∵ ‎2:8=1:4‎，∴ 方程x−2‎x−8‎‎=0‎与x‎2‎‎−5x+4=0‎是“像方程”．下列方程中与方程‎2x−1‎‎2‎‎=‎x−5‎‎2‎是“像方程”的是(        ) ‎ A.x−2‎‎2‎‎=2‎x−2‎ B.x‎2‎‎−4x+4=0‎ C.x+1‎x+3‎‎=0‎ D.‎x‎2‎‎+3x=18‎ ‎ ‎ ‎9. 下列卡片上有关二次根式的化简过程，正确的有(        ) ①‎−20‎‎−5‎‎=‎−20‎‎−5‎=‎2‎‎−5‎‎−5‎=2‎；②‎2‎3‎‎3‎‎−1‎=6−2‎‎3‎ ；③‎2‎‎−3‎‎3+‎‎2‎‎=9−2=7‎. ‎ A.①② B.②③ C.①③ D.②‎ ‎ ‎ ‎10. 欧几里得是古希腊的著名数学家，在他的《几何原本》中，形如x‎2‎‎+ax=‎b‎2‎的方程的图解法如下：如图，以a‎2‎和b为两直角边作Rt△ABC，并在斜边上截取BD=‎a‎2‎，则方程的一个正根是(        ) ‎ A.BC的长 B.CD的长 C.AD的长 D.AC的长 二、填空题 ‎ ‎ ‎ 要使二次根式x−3‎有意义，则实数x的取值范围是________． ‎ ‎ ‎ ‎ 设a，b是方程x‎2‎‎−2x−2020=0‎的两个实数根，则ab=‎________. ‎ ‎ ‎ ‎ 若一个三角形的一边长为‎4−2‎‎2‎，这边上的高为‎2‎‎−1‎，则这个三角形的面积为________. ‎ ‎ ‎ ‎ 若等腰‎△ABC的两边长恰好为一元二次方程x‎2‎‎−10x+21=0‎的两个实数根，则‎△ABC的周长为________. ‎ ‎ ‎ 第17页 共20页 ◎ 第18页 共20页 ‎ 我们把对角线互相垂直的四边形称为“垂美四边形”，如图，在“垂美四边形”ABCD中，对角线AC，BD相交于点O，AD=‎‎5‎，BC=‎‎17‎，AB‎2‎+CD‎2‎=a.为了让大家了解“垂美四边形”，小魏写了一篇倡议书，决定用微博转发的方式传播．他设计了如下的传播规则：将倡议书发表在自己的微博上，再邀请n个好友，每个好友转发之后，各自又邀请互不相同的n个好友再转发．已知经过两轮转发后，共有‎5a+1‎个人参与了宣传活动，则n的值为________. ‎ 三、解答题 ‎ ‎ ‎   ‎ ‎(1)‎计算：‎1‎‎5‎‎×‎20‎‎−‎‎5‎+|−2|‎；‎ ‎ ‎ ‎(2)‎下面是小兵同学解方程的过程，请你认真阅读，并完成相应的任务： 解方程：‎3x‎2‎−4=‎‎1‎‎2‎‎2x−8‎. 解：去括号，得‎3x‎2‎−4=x−4‎ ，‎⋯⋯‎第一步 两边都加上‎4‎，得‎3x‎2‎=x，‎⋯⋯‎第二步 两边都除以x，得‎3x=1‎，‎⋯⋯‎第三步 两边都除以‎3‎，得x=‎‎1‎‎3‎ .‎⋯⋯‎第四步 任务：①第一步去括号的依据是________律，第四步两边都除以‎3‎的依据是________，第三步开始出现错误，这一步错误的原因是________； ②请直接写出解方程的正确结果．‎ ‎ ‎ ‎ 由于‎2020‎年疫情爆发，市场对口罩的需求量大增，某口罩厂‎1‎月份日产量为‎18000‎个，为了满足市场需求，工厂从‎2‎月份起扩大生产，‎3‎月份日产量达到‎21780‎个，求口罩日产量的月平均增长率． ‎ ‎ ‎ ‎ 在‎△ABC中，AD是‎△ABC的中线，AC=‎‎20‎，AB=‎‎15‎，BC=‎‎45‎. ‎ ‎(1)‎判断AB，AC，BC的长中哪些是最简二次根式，并把不是最简二次根式的化为最简二次根式；‎ ‎ ‎ ‎(2)‎求CD+AC的长．‎ ‎ ‎ ‎ 已知关于x的一元二次方程x‎2‎‎−‎2k+1‎x+k‎2‎+k=0‎. ‎ ‎(1)‎若该方程的解为x=−2‎，求k的值；‎ ‎ ‎ ‎(2)‎求证：无论k取何值，这个方程总有两个不相等的实数根．‎ ‎ ‎ ‎ 小杨给出三条线段p，q，m的长度如下： p=‎‎14‎‎×‎‎2‎‎7‎，q=‎5‎+10‎1‎‎5‎−‎‎1‎‎2‎‎20‎，m=(‎3‎+1‎)‎‎2‎−‎3‎(‎3‎+2)‎. ‎ ‎(1)‎请你化简p，q，m；‎ ‎ ‎ ‎(2)‎某居民小区要在一块一边靠墙（墙长为‎8‎米）的空地上建一个矩形花园ABCD，花园一边靠墙，另三边用总长为pm+‎5‎q+4‎米的栅栏围成，如图所示．若AB的长为x米，当x取何值时，花园的面积为‎30‎平方米？ ‎ ‎ ‎ ‎ 阅读以上材料并思考下列问题： 已知实数a，b满足b=‎a−2‎‎+‎2−a−4‎a−1‎. ‎ ‎(1)‎求‎2ab的平方根；‎ ‎ ‎ ‎(2)‎判断以a，b+1‎，ab−1‎为边能否构成三角形，若能构成三角形，此三角形是什么形状的三角形？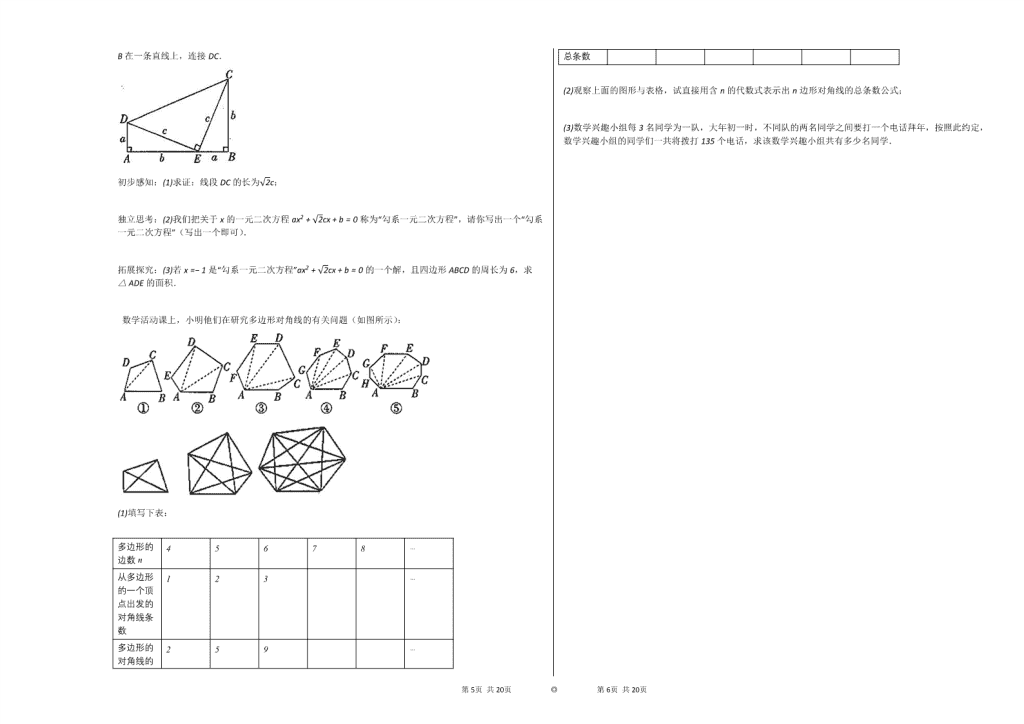并求出此三角形的面积；若不能，请说明理由．‎ ‎ ‎ 第17页 共20页 ◎ 第18页 共20页 ‎ 问题情境：勾股定理是人类最伟大的十大科学发现之一，西方称之为毕达哥拉斯定理．到目前为止，人们已经找到了‎400‎多种证明勾股定理的方法．如图所示的是美国第二十任总统加菲尔德的“总统证法”示意图，a，b，c都是Rt△ADE和Rt△BEC的三条边长，该图形由Rt△ADE和Rt△BEC拼合而成，其中，点A，E，B在一条直线上，连接DC． ‎ 初步感知：‎(1)‎求证：线段DC的长为‎2‎c；‎ ‎ ‎ 独立思考：‎(2)‎我们把关于x的一元二次方程ax‎2‎+‎2‎cx+b=0‎称为“勾系一元二次方程”，请你写出一个“勾系一元二次方程”（写出一个即可）．‎ ‎ ‎ 拓展探究：‎(3)‎若x=−1‎是“勾系一元二次方程”ax‎2‎+‎2‎cx+b=0‎的一个解，且四边形ABCD的周长为‎6‎，求‎△ADE的面积．‎ ‎ ‎ ‎ 数学活动课上，小明他们在研究多边形对角线的有关问题（如图所示）： ‎ ‎(1)‎填写下表： ‎ 多边形的边数n ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎⋯‎‎ ‎ 从多边形的一个顶点出发的对角线条数 ‎1‎ ‎2‎ ‎3‎ ‎    ‎ ‎   ‎ ‎⋯‎ 多边形的对角线的总条数 ‎2‎ ‎5‎ ‎9‎ ‎   ‎ ‎  ‎ ‎⋯‎ ‎ ‎ ‎(2)‎观察上面的图形与表格，试直接用含n的代数式表示出n边形对角线的总条数公式；‎ ‎ ‎ ‎(3)‎数学兴趣小组每‎3‎名同学为一队，大年初一时，不同队的两名同学之间要打一个电话拜年，按照此约定，数学兴趣小组的同学们一共将拨打‎135‎个电话，求该数学兴趣小组共有多少名同学．‎ 第17页 共20页 ◎ 第18页 共20页 参考答案与试题解析 ‎2020-2021学年山西临汾九年级上数学月考试卷 一、选择题 ‎1.‎ ‎【答案】‎ D ‎【考点】‎ 二次根式的定义及识别 ‎【解析】‎ 依据二次根式的定义回答即可．‎ ‎【解答】‎ 解：二次根式的定义：一般地，我们把形如aa≥0‎的式子叫做二次根式． A，‎−5‎的被开方数是‎−5‎，‎−5<0‎， 则‎−5‎无意义，故本选项不符合题意； B，当x+2<0‎时，它无意义，故本选项不符合题意； C，‎3‎‎7‎属于三次根式，故本选项不符合题意； D，‎3‎符合二次根式的定义，故本选项符合题意． 故选D．‎ ‎2.‎ ‎【答案】‎ B ‎【考点】‎ 一元二次方程的解 ‎【解析】‎ 把x=−1‎代入方程x‎2‎‎+kx=0‎得到关于k的方程，然后解关于k的方程即可．‎ ‎【解答】‎ 解：把x=−1‎代入方程x‎2‎‎+kx=0‎得‎1−k=0‎， 解得：k=1‎． 故选B．‎ ‎3.‎ ‎【答案】‎ C ‎【考点】‎ 算术平方根 ‎【解析】‎ 根据算术平方根的定义和算术平方根的性质进行解答即可得出结论.‎ ‎【解答】‎ 解：A，‎9‎‎=3≠±3‎，故此选项不符合题意； B，‎−3‎‎2‎‎=‎9‎=3≠9‎，故此选项不符合题意； C，‎5‎‎2‎‎=5‎，故此选项符合题意； D，‎−‎‎2‎‎2‎‎=2≠−2‎，故此选项不符合题意. 故选C.‎ ‎4.‎ ‎【答案】‎ A ‎【考点】‎ 解一元二次方程-配方法 ‎【解析】‎ 根据配方法即可求出答案．‎ ‎【解答】‎ 解：∵ x‎2‎‎+2x=1‎， ∴ x‎2‎‎+2x+1=2‎， ∴ x+1‎‎2‎‎=2‎. 故选A．‎ ‎5.‎ ‎【答案】‎ B ‎【考点】‎ 同类二次根式 ‎【解析】‎ 根据二次根式的性质画简各个根式，看看是否是同类二次根式，即可得出答案．‎ ‎【解答】‎ 解：A，‎6‎和‎3‎不是同类二次根式，不能合并， 故本选项不符合题意； B，‎12‎‎=2‎‎3‎和‎3‎是同类二次根式，能合并， 故本选项符合题意； C，‎2‎‎3‎‎=‎‎6‎‎3‎和‎3‎不是同类二次根式，不能合并， 故本选项不符合题意； D，‎24‎‎=2‎‎6‎和‎3‎不是同类二次根式，不能合并， 故本选项不符合题意． 故选B．‎ ‎6.‎ ‎【答案】‎ B ‎【考点】‎ 根的判别式 ‎【解析】‎ 掌握求根公式是解答本题的根本，需要知道根的判别式‎△=b‎2‎−4ac，这里可以分为‎3‎种情况：‎1‎、当‎△>0‎时，一元二次方程有‎2‎个不相等的实数根‎2‎、当‎△=0‎时，一元二次方程有‎2‎个相同的实数根‎3‎、当‎△<0‎时，一元二次方程没有实数根．‎ ‎【解答】‎ 解：利用一元二次方程的根的判别式与‎0‎的关系来判断根的情况． ∵ a=1‎，b=3‎，c=4‎， ∴ Δ=9−4×1×4‎ ‎=−7<0‎， ∴ 方程没有实数根． 故选B.‎ ‎7.‎ 第17页 共20页 ◎ 第18页 共20页 ‎【答案】‎ B ‎【考点】‎ 算术平方根在实际问题中的应用 面积作差问题 二次根式的应用 ‎【解析】‎ 根据已知的两个正方形的面积求出边长，计算大正方形的边长，然后计算面积，最后根据剩余部分的面积等于大正方形的面积减去两个小正方形的面积可得结果.‎ ‎【解答】‎ 解：两个小正方形的面积分别为‎4dm‎2‎和‎8dm‎2‎， 则这两个小正方形的边长分别是 ‎4‎‎=2(dm)‎，‎8‎‎=2‎2‎(dm)‎. 则大正方形的边长为‎2+2‎‎2‎dm. 则大正方形的面积为： ‎2+2‎‎2‎‎2‎‎=4+8‎2‎+8‎ ‎=12+8‎2‎(dm‎2‎)‎, 则余下风景画的面积为： ‎12+8‎2‎−4−8‎ ‎=8‎‎2‎dm‎2‎. 故选B.‎ ‎8.‎ ‎【答案】‎ D ‎【考点】‎ 解一元二次方程-因式分解法 ‎【解析】‎ 分别求出选项中两个方程的解，再结合“像方程”的定义即可确定结论．‎ ‎【解答】‎ 解：‎2x−1‎‎2‎‎=‎x−5‎‎2‎, ‎2x−1=x−5‎或‎2x−1=−‎x−5‎, x‎1‎‎=−4‎，x‎2‎‎=2‎. 则x‎1‎x‎2‎‎=‎−4‎‎2‎=−2‎. A，x−2‎‎2‎‎=2‎x−2‎， x−2‎x−2−2‎‎=0‎， x‎1‎‎=4 ‎，x‎2‎‎=2‎. x‎1‎x‎2‎‎=2‎，则A不符合题意； B，x‎2‎‎−4x+4=0‎， x‎1‎‎=x‎2‎=2‎， x‎1‎x‎2‎‎=1‎，则 B不符合题意； C，x+1‎x+3‎‎=0‎， x‎1‎‎=−3‎，x‎2‎‎=−1‎， x‎1‎x‎2‎‎=3‎，则C不符合题意; D，x‎2‎‎+3x=18‎， x‎2‎‎+3x−18=0‎， x‎1‎‎=−6 ‎，x‎2‎‎=3‎， x‎1‎x‎2‎‎=−2‎，则D符合题意. 故选D.‎ ‎9.‎ ‎【答案】‎ D ‎【考点】‎ 二次根式的混合运算 分母有理化 ‎【解析】‎ 根据二次根式除法法则，二次根式混合运算的法则，依次计算，即可解答.‎ ‎【解答】‎ 解：‎−20‎‎−5‎‎=‎4‎=2‎；则①错误； ‎2‎3‎‎3‎‎−1‎=2‎3‎×‎3‎−2‎‎3‎‎=6−2‎‎3‎；则②正确； ‎2‎‎−3‎‎3+‎‎2‎‎=‎2‎‎2‎−‎3‎‎2‎=2−9‎‎=−7‎；则③错误. 故选D.‎ ‎10.‎ ‎【答案】‎ C ‎【考点】‎ 一元二次方程的解 勾股定理 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：根据题意得， 设AD=x， 根据勾股定理得：‎(x+a‎2‎‎)‎‎2‎=b‎2‎+(‎a‎2‎‎)‎‎2‎， 整理得：x‎2‎‎+ax=‎b‎2‎， 则该方程的一个正根是AD的长. 故选C.‎ 二、填空题 ‎【答案】‎ x≥3‎ ‎【考点】‎ 二次根式有意义的条件 ‎【解析】‎ 直接利用二次根式的定义得出答案．‎ 第17页 共20页 ◎ 第18页 共20页 ‎【解答】‎ 解：二次根式x−3‎有意义，故x−3≥0‎， 则x的取值范围是：x≥3‎． 故答案为：x≥3‎.‎ ‎【答案】‎ ‎−2020‎ ‎【考点】‎ 根与系数的关系 ‎【解析】‎ 利用根与系数的关系求解即可．‎ ‎【解答】‎ 解：∵ a，b是方程x‎2‎‎−2x−2020=0‎的两个实数根， ∴ ab=‎−2020‎‎1‎=−2020‎． 故答案为：‎−2020‎．‎ ‎【答案】‎ ‎3‎2‎−4‎ ‎【考点】‎ 二次根式的乘法 三角形的面积 ‎【解析】‎ 直接利用三角形的面积=‎1‎‎2‎‎×‎一边的长×这边上的高，计算面积．‎ ‎【解答】‎ 解：这个三角形的面积为: ‎1‎‎2‎‎×‎4−2‎‎2‎×‎‎2‎‎−1‎ ‎=‎1‎‎2‎×2×‎‎2−‎‎2‎‎2‎‎−1‎ ‎=‎‎2−‎‎2‎‎2‎‎−1‎ ‎=3‎2‎−4‎. 故答案为：‎3‎2‎−4‎.‎ ‎【答案】‎ ‎17‎ ‎【考点】‎ 三角形三边关系 解一元二次方程-因式分解法 等腰三角形的性质 ‎【解析】‎ 用因式分解法求出方程的两个根分别是‎3‎和‎7‎，有三角形的三边关系，‎3‎为底，‎7‎为腰，可以求出三角形的周长．‎ ‎【解答】‎ 解：由题知：x‎2‎‎−10x+21=0‎, 即‎(x−3)(x−7)‎‎=0‎, 解得x‎1‎‎=3‎，x‎2‎‎=7‎. ∵ 三角形是等腰三角形，必须满足三角形三边的关系， ∴ 腰长是‎7‎，底边是‎3‎， 故周长为：‎7+7+3‎‎=17‎． 故答案为：‎17‎.‎ ‎【答案】‎ ‎10‎ ‎【考点】‎ 勾股定理的综合与创新 由实际问题抽象出一元二次方程 解一元二次方程-配方法 勾股定理 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：根据勾股定理，得： AB‎2‎+CD‎2‎‎=AO‎2‎+BO‎2‎+OC‎2‎+OD‎2‎， AD‎2‎+BC‎2‎‎=AO‎2‎+DO‎2‎+OC‎2‎+OB‎2‎， ∴ AB‎2‎+CD‎2‎=AD‎2‎+BC‎2‎， ∵ AD=‎‎5‎ ，BC=‎‎17‎， ∴ AB‎2‎+CD‎2‎=a ‎=(‎5‎‎)‎‎2‎+(‎‎17‎‎)‎‎2‎ ‎=5+17=22‎， ∴ ‎5a+1=5×22+1=111‎，根据题意， 得‎1+n+n‎2‎=111‎． ∴ n‎2‎‎+n−110=0‎． ∴ n‎1‎‎=10‎，n‎2‎‎=−11‎（舍去）， ∴ n=10‎. 故答案为：‎10‎．‎ 三、解答题 ‎【答案】‎ 解：‎(1)‎原式‎=‎1‎‎5‎‎×20‎−‎1‎‎5‎‎×5‎+2‎ ‎=‎4‎−‎1‎+2‎ ‎=2−1+2‎ ‎=3‎.‎ ‎(2)‎‎①乘法分配； 等式的性质‎2‎； 两边除以一个可能为‎0‎的式子. ②由题知：‎3x‎2‎−x=0‎， 即x(3x−1)=0‎， 解得x‎1‎‎=0‎，x‎2‎‎=‎‎1‎‎3‎.‎ ‎【考点】‎ 解一元二次方程-配方法 二次根式的化简求值 第17页 共20页 ◎ 第18页 共20页 解一元一次方程 绝对值 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：‎(1)‎原式‎=‎1‎‎5‎‎×20‎−‎1‎‎5‎‎×5‎+2‎ ‎=‎4‎−‎1‎+2‎ ‎=2−1+2‎ ‎=3‎.‎ ‎(2)‎‎①乘法分配； 等式的性质‎2‎； 两边除以一个可能为‎0‎的式子. ②由题知：‎3x‎2‎−x=0‎， 即x(3x−1)=0‎， 解得x‎1‎‎=0‎，x‎2‎‎=‎‎1‎‎3‎.‎ ‎【答案】‎ 解：设口罩日产量的月平均增长率为x， 根据题意，得‎18000(1+x‎)‎‎2‎=21780‎， 即‎(1+x‎)‎‎2‎=1.21‎， 解得：x‎1‎‎=0.1‎，x‎2‎‎=−2.1‎（舍去）. 答：口罩日产量的月平均增长率为‎10%‎.‎ ‎【考点】‎ 一元二次方程的应用--增长率问题 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：设口罩日产量的月平均增长率为x， 根据题意，得‎18000(1+x‎)‎‎2‎=21780‎， 即‎(1+x‎)‎‎2‎=1.21‎， 解得：x‎1‎‎=0.1‎，x‎2‎‎=−2.1‎（舍去）. 答：口罩日产量的月平均增长率为‎10%‎.‎ ‎【答案】‎ 解：‎(1)‎AB的长是最简二次根式， AC和BC的长不是最简二次根式. AC=‎‎20‎‎=‎‎4×5‎‎=2‎‎5‎， BC=‎‎45‎‎=‎‎5×9‎‎=3‎‎5‎.‎ ‎(2)‎‎∵ AD是‎△ABC的中线， ∴ CD=‎1‎‎2‎BC， ∴ CD+AC   ‎=‎1‎‎2‎×3‎5‎+2‎‎5‎  ‎=‎‎7‎‎5‎‎2‎.‎ ‎【考点】‎ 三角形的中线 二次根式的混合运算 最简二次根式 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：‎(1)‎AB的长是最简二次根式， AC和BC的长不是最简二次根式. AC=‎‎20‎‎=‎‎4×5‎‎=2‎‎5‎， BC=‎‎45‎‎=‎‎5×9‎‎=3‎‎5‎.‎ ‎(2)‎‎∵ AD是‎△ABC的中线， ∴ CD=‎1‎‎2‎BC， ∴ CD+AC   ‎=‎1‎‎2‎×3‎5‎+2‎‎5‎  ‎=‎‎7‎‎5‎‎2‎.‎ ‎【答案】‎ ‎(1)‎解：将x=−2‎代入得： ‎(−2‎)‎‎2‎−(2k+1)×(−2)+k‎2‎+k=0‎， ∴ ‎4+4k+2+k‎2‎+k=0‎， 即k‎2‎‎+5k+6=0‎， ∴ ‎(k+2)(k+3)=0‎， ∴ k‎1‎‎=−2‎，k‎2‎‎=−3‎.‎ ‎(2)‎证明：∵ Δ=b‎2‎−4ac ‎=(2k+1‎)‎‎2‎−4×1×(k‎2‎+k)‎ ‎=4k‎2‎+4k+1−4k‎2‎−4k‎=1>0‎， ∴ 这个方程总有两个不相等的实数根.‎ ‎【考点】‎ 根的判别式 一元二次方程的解 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ ‎(1)‎解：将x=−2‎代入得： ‎(−2‎)‎‎2‎−(2k+1)×(−2)+k‎2‎+k=0‎， ∴ ‎4+4k+2+k‎2‎+k=0‎， 即k‎2‎‎+5k+6=0‎， ∴ ‎(k+2)(k+3)=0‎， ∴ k‎1‎‎=−2‎，k‎2‎‎=−3‎.‎ 第17页 共20页 ◎ 第18页 共20页 ‎(2)‎证明：∵ Δ=b‎2‎−4ac ‎=(2k+1‎)‎‎2‎−4×1×(k‎2‎+k)‎ ‎=4k‎2‎+4k+1−4k‎2‎−4k‎=1>0‎， ∴ 这个方程总有两个不相等的实数根.‎ ‎【答案】‎ 解：‎(1)‎p=‎‎14‎‎×‎‎2‎‎7‎‎=‎14×2‎‎7‎=‎4‎=2‎， q=‎5‎+10‎1‎‎5‎−‎‎1‎‎2‎‎20‎ ‎=‎5‎+2‎5‎−‎5‎=2‎‎5‎， m=(‎3‎+1‎)‎‎2‎−‎3‎(‎3‎+2)‎ ‎=3+2‎3‎+1−3−2‎3‎=1‎.‎ ‎(2)‎由‎(1)‎知p=2‎，q=2‎‎5‎，m=1‎， ∴ pm+‎5‎q+4‎ ‎=2×1+‎5‎×2‎5‎+4‎ ‎=2+10+4=16‎. ∵ AB+BC+CD=16‎，AB=CD，AB=x， ∴ BC=16−2x， ∴ x(16−2x)=30‎， 即x‎2‎‎−8x+15=0‎， 解得：x=5‎或x=3‎. 当x=5‎时，BC=16−2×5=6<8‎，符合题意； 当x=3‎时，BC=16−2×3=10>8‎，不符合题意，舍去. ∴ x的值为‎5‎，即AB=5‎米.‎ ‎【考点】‎ 解一元二次方程-因式分解法 二次根式的化简求值 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：‎(1)‎p=‎‎14‎‎×‎‎2‎‎7‎‎=‎14×2‎‎7‎=‎4‎=2‎， q=‎5‎+10‎1‎‎5‎−‎‎1‎‎2‎‎20‎ ‎=‎5‎+2‎5‎−‎5‎=2‎‎5‎， m=(‎3‎+1‎)‎‎2‎−‎3‎(‎3‎+2)‎ ‎=3+2‎3‎+1−3−2‎3‎=1‎.‎ ‎(2)‎由‎(1)‎知p=2‎，q=2‎‎5‎，m=1‎， ∴ pm+‎5‎q+4‎ ‎=2×1+‎5‎×2‎5‎+4‎ ‎=2+10+4=16‎. ∵ AB+BC+CD=16‎，AB=CD，AB=x， ∴ BC=16−2x， ∴ x(16−2x)=30‎， 即x‎2‎‎−8x+15=0‎， 解得：x=5‎或x=3‎. 当x=5‎时，BC=16−2×5=6<8‎，符合题意； 当x=3‎时，BC=16−2×3=10>8‎，不符合题意，舍去. ∴ x的值为‎5‎，即AB=5‎米.‎ ‎【答案】‎ 解：‎(1)‎∵ a−2≥0,‎‎2−a≥0,‎ ∴ a≥2,‎a≤2,‎ ∴ a=2‎，b=4‎. ∴ ‎2ab‎=‎‎2×2×4‎‎=4‎， ∴ ‎2ab的平方根为‎2‎．‎ ‎(2)‎由‎(1)‎知：a‎=‎‎2‎，b+1‎‎=‎‎4+1‎‎=‎‎5‎,  ab−1‎‎=‎‎2×4−1‎‎=‎‎7‎， ‎∵‎2‎+‎5‎>‎‎7‎， ∴ 以a，b+1‎，ab−1‎为边能构成三角形． ∵ ‎(a‎)‎‎2‎+(b+1‎‎)‎‎2‎=2+5=7‎，‎(ab−1‎‎)‎‎2‎=7‎， ∴ ‎(a‎)‎‎2‎+(b+1‎‎)‎‎2‎=(‎ab−1‎‎)‎‎2‎． ∴ 能构成直角三角形， ∴ 此三角形的面积为： ‎1‎‎2‎‎×a×‎b+1‎ ‎=‎1‎‎2‎×‎2‎×‎‎5‎ ‎=‎‎10‎‎2‎．‎ ‎【考点】‎ 三角形三边关系 三角形的面积 二次根式的混合运算 勾股定理的逆定理 非负数的性质：算术平方根 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：‎(1)‎∵ a−2≥0,‎‎2−a≥0,‎ ∴ a≥2,‎a≤2,‎ ∴ a=2‎，b=4‎. ∴ ‎2ab‎=‎‎2×2×4‎‎=4‎， ∴ ‎2ab的平方根为‎2‎．‎ ‎(2)‎由‎(1)‎知：a‎=‎‎2‎，b+1‎‎=‎‎4+1‎‎=‎‎5‎,  ab−1‎‎=‎‎2×4−1‎‎=‎‎7‎， ‎∵‎2‎+‎5‎>‎‎7‎， ∴ 以a，‎ 第17页 共20页 ◎ 第18页 共20页 b+1‎‎，ab−1‎为边能构成三角形． ∵ ‎(a‎)‎‎2‎+(b+1‎‎)‎‎2‎=2+5=7‎，‎(ab−1‎‎)‎‎2‎=7‎， ∴ ‎(a‎)‎‎2‎+(b+1‎‎)‎‎2‎=(‎ab−1‎‎)‎‎2‎． ∴ 能构成直角三角形， ∴ 此三角形的面积为： ‎1‎‎2‎‎×a×‎b+1‎ ‎=‎1‎‎2‎×‎2‎×‎‎5‎ ‎=‎‎10‎‎2‎．‎ ‎【答案】‎ ‎(1)‎证明：∵ ‎∠DEC=‎‎90‎‎∘‎， ∴ 根据勾股定理可得： DC=‎DE‎2‎‎+CE‎2‎ ‎=‎c‎2‎‎+‎c‎2‎ ‎=‎2‎c‎2‎=‎2‎c．‎ ‎(2)‎解：答案不唯一，如取a=1‎，b=3‎， 根据勾股定理，得c=‎1‎‎2‎‎+‎‎3‎‎2‎=‎‎10‎， ∴ “勾系一元二次方程”为x‎2‎‎+‎10‎×‎2‎x+3=0‎， 即x‎2‎‎+2‎5‎x+3=0‎．‎ ‎(3)‎解：当x=−1‎时， “勾系一元二次方程”为a‎−1‎‎2‎+‎2‎c×‎−1‎+b=0‎， 即a−‎2‎c+b=0‎， ∴ a+b=‎2‎c． ∵ 四边形ABCD的周长为‎6‎， ∴ ‎2a+2b+‎2‎c=6‎， ∴ ‎2‎2‎c+‎2‎c=6‎， ∴ ‎3‎2‎c=6‎，∴ c=‎‎2‎． ∴ a‎2‎‎+b‎2‎=c‎2‎=2‎，a+b=2‎， ∵ a+b‎2‎‎=a‎2‎+b‎2‎+2ab， ∴ ‎2ab=‎2‎‎2‎−2=2‎，∴ ab=1‎. ∴ ‎△ADE的面积为‎1‎‎2‎ab=‎1‎‎2‎×1=‎‎1‎‎2‎．‎ ‎【考点】‎ 三角形的面积 一元二次方程的解 勾股定理 ‎【解析】‎ ‎（‎1‎）证明：∵ ‎∠DEC=‎‎90‎‎∘‎，∴ 根据勾股定理可得DC=DE‎2‎‎+CE‎2‎=c‎2‎‎+‎c‎2‎=‎2‎c‎2‎=‎2‎c．‎ ‎ ‎ ‎【解答】‎ ‎(1)‎证明：∵ ‎∠DEC=‎‎90‎‎∘‎， ∴ 根据勾股定理可得： DC=‎DE‎2‎‎+CE‎2‎ ‎=‎c‎2‎‎+‎c‎2‎ ‎=‎2‎c‎2‎=‎2‎c．‎ ‎(2)‎解：答案不唯一，如取a=1‎，b=3‎， 根据勾股定理，得c=‎1‎‎2‎‎+‎‎3‎‎2‎=‎‎10‎， ∴ “勾系一元二次方程”为x‎2‎‎+‎10‎×‎2‎x+3=0‎， 即x‎2‎‎+2‎5‎x+3=0‎．‎ ‎(3)‎解：当x=−1‎时， “勾系一元二次方程”为a‎−1‎‎2‎+‎2‎c×‎−1‎+b=0‎， 即a−‎2‎c+b=0‎， ∴ a+b=‎2‎c． ∵ 四边形ABCD的周长为‎6‎， ∴ ‎2a+2b+‎2‎c=6‎， ∴ ‎2‎2‎c+‎2‎c=6‎， ∴ ‎3‎2‎c=6‎，∴ c=‎‎2‎． ∴ a‎2‎‎+b‎2‎=c‎2‎=2‎，a+b=2‎， ∵ a+b‎2‎‎=a‎2‎+b‎2‎+2ab， ∴ ‎2ab=‎2‎‎2‎−2=2‎，∴ ab=1‎. ∴ ‎△ADE的面积为‎1‎‎2‎ab=‎1‎‎2‎×1=‎‎1‎‎2‎．‎ ‎【答案】‎ 解：‎(1)‎由题得： ‎ 多边形的边数n ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎⋯‎ 从多边形的一个顶点出发的对角线条数 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎⋯‎ 多边形的对角线的总条数 ‎2‎ ‎5‎ ‎9‎ ‎14‎ ‎20‎ ‎⋯‎ ‎(2)‎由题知：‎1‎‎2‎n(n−3)‎.‎ ‎(3)‎设该数学兴趣小组有x名同学， 根据题意，‎1‎‎2‎xx−3‎=135‎， 即x‎2‎‎−3x−270=0‎， 解得x=−15‎（不合题意，舍去）或x=18‎. 答：该数学兴趣小组共有‎18‎名同学．‎ ‎【考点】‎ 多边形的对角线 多边形 由实际问题抽象出一元二次方程 ‎【解析】‎ ‎ ‎ ‎ ‎ 第17页 共20页 ◎ 第18页 共20页 ‎ ‎ ‎【解答】‎ 解：‎(1)‎由题得： ‎ 多边形的边数n ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎⋯‎ 从多边形的一个顶点出发的对角线条数 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎⋯‎ 多边形的对角线的总条数 ‎2‎ ‎5‎ ‎9‎ ‎14‎ ‎20‎ ‎⋯‎ ‎(2)‎由题知：‎1‎‎2‎n(n−3)‎.‎ ‎(3)‎设该数学兴趣小组有x名同学， 根据题意，‎1‎‎2‎xx−3‎=135‎， 即x‎2‎‎−3x−270=0‎， 解得x=−15‎（不合题意，舍去）或x=18‎. 答：该数学兴趣小组共有‎18‎名同学．‎ 第17页 共20页 ◎ 第18页 共20页