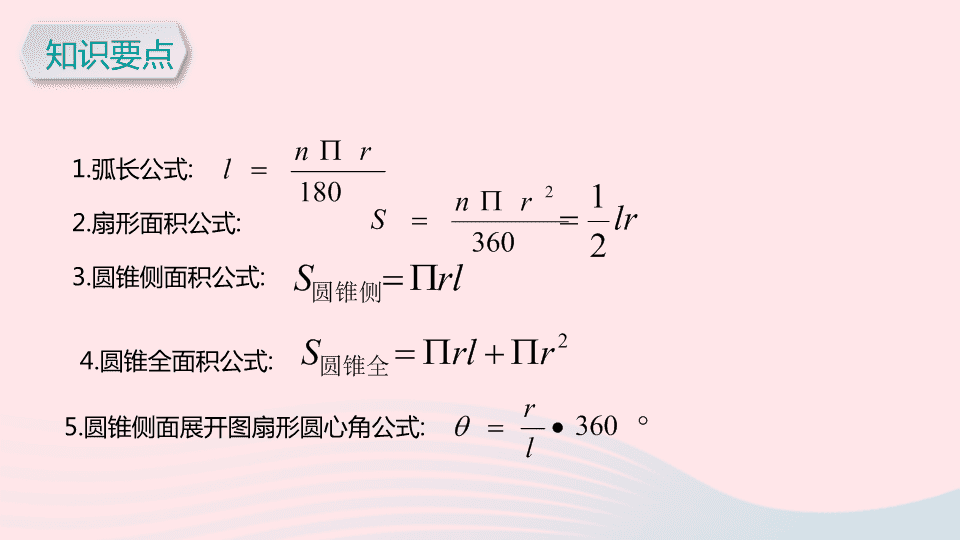九年级数学上册第二十四章圆24-3圆与多边形4弧长扇形面积圆锥表面积计算教学课件新版 人教版 15页

第 24 章 弧长、扇形面积、圆锥表面积计算 24.3圆与多边形（4） 1. 弧长公式 : 2. 扇形面积公式 : 3. 圆锥侧面积公式 : 4. 圆锥全面积公式 : 5. 圆锥侧面展开图扇形圆心角公式 : 知识要点 1. 已知弧长为 4∏cm, 它所对的圆心角为 120°, 那么它所对的弦长为 ( ) 2. 在⊙ O 中 , 所对的圆心角为 60°, 且弦 AB=5cm, 则 的长为 ( ) C A 基础训练 3. 如果扇形的半径是 6 ，所含的弧长是 5π ，那么扇形的面积是 ( ) A. ５ π B. １０ π C. １５ π D. ３０ π C 4. 如图，正方形的边长为 a ，分别以两个对角顶点为圆心， a 为半径画弧，则图中阴影部分的面积为 ( ) B A.4-2π B.2π －４ C.π － 2 D. ２（４－ π ） 课前热身 5. 一个形如圆锥的冰淇淋纸筒，其底面直径为６ cm, 母线长５ cm, 则它的侧面积是（　　　　） Ａ .66∏ Ｂ .30∏ Ｃ .28∏ Ｄ .15∏ 6. 在半径为 6cm 的圆中， 120° 的圆心角所对的弧长为 . 7. 扇形半径为 12, 面积为 9∏, 它的圆心角等于 度 D 4∏cm 22.5 8. 已知扇形的面积为 24∏ , 弧长为８∏ cm, 则扇形的半径是 　　　 cm, 圆心角是 　　　　 度 9. 已知扇形的面积是 12 , 半径是 8cm, 则扇形周长是 　　 ． 10. 圆锥的底面半径是 1cm, 母线是 2cm, 则高是 cm, 侧面积是 ，全面积是 , 　 6 240 19 2∏ 3∏ 例 1 ：已知一个圆锥的轴截面△ ABC 是等边三角形，它 的表面积为 75π , 求这个圆锥的底面半径和母线的长。 A B C O 做一做 生活中的圆锥侧面积计算 已知圆锥的底面半径为 8cm, 母线长 20cm, 求它的侧面展开图的圆心角和表面积 . 练习： 一个圆锥的侧面展开图是半径为 18cm ，圆心角为 240 0 的扇形，求这个圆锥的高。 例 2: 如图 , 水平放置的圆柱形排水管的截面半径为 12cm, 截面中有水部分弓形的高为 6cm, 求截面中有水部分弓形的面积 . O A B 6cm 【 例 3】 圆心角都是 90° 的扇形 OAB 与扇形 OCD 如图所示那样叠放在一起，连结 AC 、 BD (1) 求证：△ AOC≌△BOD ； (2) 若 OA=3 cm ， OC=1 cm ，求阴影部分的面积 . 典型例题解析 S 阴 =S 扇 AOB -S 扇 COD = π(OA 2 -OC 2 )= π(9-1)= ２ π 【 解析 】(1) 同圆中的半径相等，即 OA=OB ， OC=OD. 再由∠ AOB=∠COD=90° 得∠ 1=∠2 ，所以△ AOC≌△BOD (2) 阴影部分一般都是不规则的图形，不能直接用面积公式求解，通常有两条思路，一是转化成规则图形面积的和、差；二是进行图形的割补 . 此题是利用图形的割补，把图形△ OAC 放到△ OBD 的位置 ( 因为△ AOC≌△BOD) ，则阴影部分的面积为圆环的面积 【 例 4 一块等边三角形的木板，边长为 1 ，现将木板沿水平线翻滚 ( 如图 ) ，那么 B 点从开始至结束所走过的路径长度为 ( ) A. B. C. ４ D. ２＋ B 典型例题解析 故选 B. 【 解析 】 这个题目有些同学一看，认为没有选项，他说从 B 到 B ，长度为 3. 其实不然，从 BBB 这是一个两次旋转的过程，相当于以 C 为中心， B 绕点 C 旋转 120° ，再绕点 A 同方向旋转 120° ，因此 B 所走过的路径长是两段圆弧长，即 l= A B C 思考题 : 、如图，圆锥的底面半径为 1 ，母线长为 3 ，一只蚂蚁要从底面圆周上一点 B 出发，沿圆锥侧面爬到过母线 AB 的轴截面上另一母线 AC 上，问它爬行的最短路线是多少？