鄂尔多斯专版2020中考数学复习方案题型突破08类比拓展应用型问题课件 159页

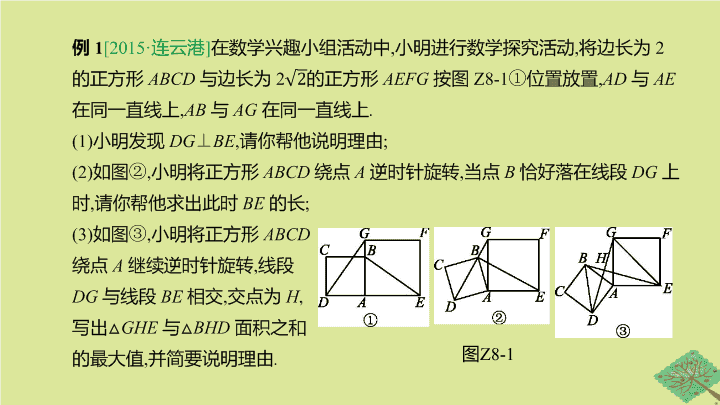
题型突破（八） 类比拓展应用型问题 类型一　旋转结构 　　 解决此类问题时 , 需仔细观察图形旋转前后相关的线段之间的数量关系、位置关系 , 相关的角的变化及角与角之间的关系 , 从中提炼出基本图形和常用模型 , 如旋转产生的等腰三角形等 , 进而借助全等 ( 相似 ) 三角形转化 , 结合勾股定理、基本图形的性质等其他知识求解 . 图 Z8-1 【 分层分析 】 (1) 由四边形 ABCD 与四边形 AEFG 为正方形 , 利用正方形的性质得到两邻边相等 , 且夹角相等 , ∠ DAG = ∠ BAE =90°, 可得 :△ 　　　　 ≌△ 　　　　 , 利用全等三角形的对应角相等得∠ 　　　　 = ∠ 　　　　 , 延长 EB 交 DG 于点 H , 利用等角的余角相等得到∠ 　　　　 =90°, 利用垂直的定义即可得 DG ⊥ BE ;  图 Z8-1 【 分层分析 】 (2) 同 (1) 可得 :△ 　　　 ≌△ 　 　　 , 利用全等三角形的对应边相等得到 　　 　 = 　　　　 , 过点 A 作 AM ⊥ DG 于点 M , 则∠ AMD = ∠ AMG =90°, 在 Rt△ AMD 中 , 求出 DM 的长 , 根据勾股定理求出 GM 的长 , 进而确定出 DG 的长 , 即为 BE 的长 ;  图 Z8-1 【 分层分析 】 (3) 对于 △ EGH , 点 H 在以 EG 为直径的圆上 , 即当点 H 与点 A 重合时 ,△ EGH 的高最大 , 即面积最大 ; 对于 △ BDH , 点 H 在以 BD 为直径的圆上 , 即当点 H 与点 A 重合时 ,△ BDH 的高最大 , 即面积最大 , 即可确定出面积和的最大值 . 解 :(3)△ GHE 与 △ BHD 面积之和的最大值为 6 . 理由 : 对于 △ EGH , 点 H 在以 EG 为直径的圆上 , ∴当点 H 与点 A 重合时 ,△ EGH 的高最大 , 即面积最大 ; 对于 △ BDH , 点 H 在以 BD 为直径的圆上 , ∴当点 H 与点 A 重合时 ,△ BDH 的高最大 , 即面积最大 , 则 △ GHE 与 △ BHD 面积之和的最大值为 2+4=6 . 【 方法点析 】 旋转变换多用在等腰三角形、正三角形、正方形等规则的图形上 , 其功能是利用旋转变换可以使图形发生重组 , 使分散的条件得以集中 , 并运用旋转的 “ 不变性 ” 使一些问题迎刃而解 , 常用的辅助线作法有 : (1) 图形中出现等边三角形时 , 通常旋转 60°; 出现等腰直角三角形、正方形时 , 通常旋转 90° . (2) 图形中有线段的中点 , 通常旋转 180° . (3) 图形中出现有公共端点的线段 , 通常旋转夹角的度数 . (4) 共端点或共线的三条线段若想要转化到同一个三角形里 , 通常考虑旋转 . 1 . 在 △ ABC 中 , ∠ C =90°, AC = BC = a , 将一块三角板的直角顶点放在斜边 AB 的中点 P 处 , 将三角板绕点 P 旋转 , 三角板与两直角边分别交于 D , E 两点 . (1) 图 Z8-2 ①中 , 线段 PD 与 PE 的数量关系是 　　　　　　 .  (2) 如图② , 在旋转过程中 , 判断 △ PDE 的形状 , 并给予证明 . (3) 在旋转过程中 , 四边形 PDCE 的面积是否发生变化 ? 若不变 , 求出面积的值 ( 用含 a 的式子表示 ); 若改变 , 请说明理由 . | 题型精练 | 图 Z8-2 PD = PE 1 . 在 △ ABC 中 , ∠ C =90°, AC = BC = a , 将一块三角板的直角顶点放在斜边 AB 的中点 P 处 , 将三角板绕点 P 旋转 , 三角板与两直角边分别交于 D , E 两点 . (2) 如图② , 在旋转过程中 , 判断 △ PDE 的形状 , 并给予证明 . 图 Z8-2 1 . 在 △ ABC 中 , ∠ C =90°, AC = BC = a , 将一块三角板的直角顶点放在斜边 AB 的中点 P 处 , 将三角板绕点 P 旋转 , 三角板与两直角边分别交于 D , E 两点 . (3) 在旋转过程中 , 四边形 PDCE 的面积是否发生变化 ? 若不变 , 求出面积的值 ( 用含 a 的式子表示 ); 若改变 , 请说明理由 . 图 Z8-2 2 . [2018· 益阳 ] 如图 Z8-3 ① , 在矩形 ABCD 中 , E 是 AD 的中点 , 以点 E 为直角顶点的直角三角形 EFG 的两边 EF , EG 分别过点 B , C , ∠ F =30° . (1) 求证 : BE = CE ; (2) 将 △ EFG 绕点 E 按顺时针方向旋转 , 当旋转到 EF 与 AD 重合时停止转动 , 若 EF , EG 分别与 AB , BC 相交于点 M , N ( 如图② ) . ①求证 :△ BEM ≌△ CEN ; ②若 AB =2, 求 △ BMN 面 积的最大值 ; ③当旋转停止时 , 点 B 恰 好在 FG 上 ( 如图③ ), 求 sin ∠ EBG 的值 . 图 Z8-3 解 :(1) 证明 : ∵四边形 ABCD 为矩形 , ∴∠ A = ∠ D =90°, AB = DC. ∵ E 为 AD 中点 , ∴ AE = DE , ∴ △ ABE ≌△ DCE , ∴ BE = CE. 2 . [2018· 益阳 ] 如图 Z8-3 ① , 在矩形 ABCD 中 , E 是 AD 的中点 , 以点 E 为直角顶点的直角三角形 EFG 的两边 EF , EG 分别过点 B , C , ∠ F =30° . (2) 将 △ EFG 绕点 E 按顺时针方向旋转 , 当旋转到 EF 与 AD 重合时停止转动 , 若 EF , EG 分别与 AB , BC 相交于点 M , N ( 如图② ) . ①求证 :△ BEM ≌△ CEN ; ②若 AB =2, 求 △ BMN 面 积的最大值 ; ③当旋转停止时 , 点 B 恰 好在 FG 上 ( 如图③ ), 求 sin ∠ EBG 的值 . 图 Z8-3 类型二　折叠结构 　　 折叠即轴对称 , 解决此类问题要抓住折叠的本质 , 充分利用轴对称的相关性质 , 利用好折痕的双线作用 : ①对应线段夹角的角平分线 ; ②对应点连线的垂直平分线 . 求解时注意从中提炼基本图形 , 如折叠会产生角平分线 , 角平分线 + 平行线可得等腰三角形等 , 进而结合图形本身的性质借助边角关系、相似等寻找解题途径 . 图 Z8-4 解 :(1) 证明 : 由折叠可得 : AE = A'E = GE , BC = CH , ∵四边形 ABCD 是矩形 , ∴ A'E = BC , ∴ EG = CH. 图 Z8-4 1 . [2017· 济宁 ] 实验探究 : (1) 如图 Z8-5 ① , 对折矩形纸片 ABCD , 使 AD 与 BC 重合 , 得到折痕 EF , 把纸片展开 ; 再一次折叠纸片 , 使点 A 落在 EF 上 , 并使折痕经过点 B , 得到折痕 BM , 同时得到线段 BN , MN. 请你观察图① , 猜想∠ MBN 的度数是多少 , 并证明你的结论 . (2) 将图①中的三角形纸片 BMN 剪下 , 如图② . 折叠该纸片 , 探究 MN 与 BM 的数量关系 . 写出折叠方案 , 并结合方案证明你的结论 . | 题型精练 | 图 Z8-5 1 . [2017· 济宁 ] 实验探究 : (2) 将图①中的三角形纸片 BMN 剪下 , 如图② . 折叠该纸片 , 探究 MN 与 BM 的数量关系 . 写出折叠方案 , 并结合方案证明你的结论 . 图 Z8-5 2 . [2016· 十堰 ] 如图 Z8-6, 将矩形纸片 ABCD ( AD>AB ) 折叠 , 使点 C 刚好落在线段 AD 上 , 且折痕分别与边 BC , AD 相交 , 设折叠后点 C , D 的对应点分别为点 G , H , 折痕分别与边 BC , AD 相交于点 E , F. (1) 判断四边形 CEGF 的形状 , 并证明你的结论 ; (2) 若 AB =3, BC =9, 求线段 CE 的取值范围 . 图 Z8-6 解 :(1) 四边形 CEGF 为菱形 . 证明 : ∵四边形 ABCD 是矩形 , ∴ AD ∥ BC , ∴∠ GFE = ∠ FEC , ∵图形翻折后点 C 与点 G 重合 , EF 为折痕 , ∴∠ GEF = ∠ FEC , ∴∠ GFE = ∠ GEF , ∴ GF = GE , ∵图形翻折后 EC 与 GE 完全重合 , ∴ GE = EC , ∴ GF = EC , ∴四边形 CEGF 为平行四边形 , ∴四边形 CEGF 为菱形 . 2 . [2016· 十堰 ] 如图 Z8-6, 将矩形纸片 ABCD ( AD>AB ) 折叠 , 使点 C 刚好落在线段 AD 上 , 且折痕分别与边 BC , AD 相交 , 设折叠后点 C , D 的对应点分别为点 G , H , 折痕分别与边 BC , AD 相交于点 E , F. (2) 若 AB =3, BC =9, 求线段 CE 的取值范围 . 图 Z8-6 解 :(2) 如图① , 当 F 与 D 重合时 , CE 取最小值 , 由 (1) 得四边形 CEGF 是菱形 , ∴ CE = CD = AB =3; 如图② , 当 G 与 A 重合时 , CE 取最大值 , 由折叠的性质得 AE = CE , ∵∠ B =90°, ∴ AE 2 = AB 2 + BE 2 , 即 CE 2 =3 2 +(9- CE ) 2 , ∴ CE =5, ∴线段 CE 的取值范围为 3≤ CE ≤5 . 类型三　一线三等角模型 　　 一线三等角模型是全等与相似的基本模型 , 解决这类题目的关键是寻找到问题中的全等或相似的基本图形 , 从而建立边角之间的数量关系来解决问题 . 例 3 [2017·岳阳] 问题背景:已知∠ EDF 的顶点 D 在△ ABC 的边 AB 所在直线上(不与 A , B 重合), DE 交 AC 所在直线于点 M , DF 交 BC 所在直线于点 N ,记△ ADM 的面积为 S 1 ,△ BND 的面积为 S 2 . (1) 【 初步尝试 】 如图 Z8-7 ① , 当 △ ABC 是等边三角形 , AB =6, ∠ EDF = ∠ A , 且 DE ∥ BC , AD =2 时 , 则 S 1 · S 2 = 　　　　 ;  图 Z8-7 (2) 【 类比探究 】 在 (1) 的条件下 , 先将点 D 沿 AB 平移 , 使 AD =4, 再将∠ EDF 绕点 D 旋转至如图②所示位置 , 求 S 1 · S 2 的值 ; 图 Z8-7 (3) 【 延伸拓展 】 当 △ ABC 是等腰三角形时 , 设∠ B = ∠ A = ∠ EDF = α. ①如图③ , 当点 D 在线段 AB 上运动时 , 设 AD = a , BD = b , 求 S 1 · S 2 的表达式 ( 结果用 a , b 和 α 的三角函数表示 ) . ②如图④ , 当点 D 在 BA 的延长线上运动时 , 设 AD = a , BD = b , 直接写出 S 1 · S 2 的表达式 , 不必写出解答过程 . 图 Z8-7 【 分层分析 】 (1) 首先证明 △ ADM ,△ BDN 都是等边三角形 , 可得 S 1 = 　　　　 , S 2 = 　　　　 , 由此即可解决问题 ;  解 :(1)12 例 3 [2017·岳阳] 问题背景:已知∠ EDF 的顶点 D 在△ ABC 的边 AB 所在直线上(不与 A , B 重合), DE 交 AC 所在直线于点 M , DF 交 BC 所在直线于点 N ,记△ ADM 的面积为 S 1 ,△ BND 的面积为 S 2 . (2) 【 类比探究 】 在 (1) 的条件下 , 先将点 D 沿 AB 平移 , 使 AD =4, 再将∠ EDF 绕点 D 旋转至如图②所示位置 , 求 S 1 · S 2 的值 ; 图 Z8-7 例 3 [2017·岳阳] 问题背景:已知∠ EDF 的顶点 D 在△ ABC 的边 AB 所在直线上(不与 A , B 重合), DE 交 AC 所在直线于点 M , DF 交 BC 所在直线于点 N ,记△ ADM 的面积为 S 1 ,△ BND 的面积为 S 2 . (3) 【 延伸拓展 】 当 △ ABC 是等腰三角形时 , 设∠ B = ∠ A = ∠ EDF = α. ①如图③ , 当点 D 在线段 AB 上运动时 , 设 AD = a , BD = b , 求 S 1 · S 2 的表达式 ( 结果用 a , b 和 α 的三角函数表示 ) . ②如图④ , 当点 D 在 BA 的延长线上运动时 , 设 AD = a , BD = b , 直接写出 S 1 · S 2 的表达式 , 不必写出解答过程 . 图 Z8-7 【 方法点析 】 在直线 AB 上有一点 P , 以 A , B , P 为顶点的∠ 1, ∠ 2, ∠ 3 相等 , ∠ 1, ∠ 2 的一条边在直线 AB 上 , 另一条边在 AB 同侧 , ∠ 3 两边所在的直线分别交∠ 1, ∠ 2 非公共边所在的直线于点 C , D. 1 . 当点 P 在线段 AB 上 , 且∠ 3 两边在 AB 同侧时 . (1) 如图 Z8-8, 若∠ 1 为直角 , 则 △ ACP ∽△ BPD. 图 Z8-8 (2) 如图 Z8-9, 若∠ 1 为锐角 , 则 △ ACP ∽△ BPD. 图 Z8-9 (3) 如图 Z8-10, 若∠ 1 为钝角 , 则 △ ACP ∽△ BPD. 图 Z8-10 2 . 当点 P 在 AB 或 BA 的延长线上 , 且∠ 3 两边在 AB 同侧时 . 如图 Z8-11, 则 △ ACP ∽△ BPD. 图 Z8-11 3 . 当点 P 在 AB 或 BA 的延长线上 , 且∠ 3 两边在 AB 异侧时 . 如图 Z8-12, 则 △ ACP ∽△ BPD. 图 Z8-12 | 题型精练 | 图 Z8-13 [ 答案 ] D 　 图 Z8-14 图 Z8-14 3 . [2019· 兰州 ] 通过对下面数学模型的研究学习 , 解决下面的问题 . 【 模型呈现 】 如图 Z8-15, 在 Rt△ ABC 中 , ∠ ACB =90°, 将斜边 AB 绕点 A 顺时针旋转 90° 得到 AD , 过点 D 作 DE ⊥ AC 于点 E , 可以推理得到 △ ABC ≌△ DAE , 进而得到 AC = DE , BC = AE , 我们把这个数学模型称为 “K 型 ” . 图 Z8-15 推理过程如下 : 图 Z8-16 【 模型应用 】 如图 Z8-17,Rt△ ABC 内接于☉ O , ∠ ACB =90°, BC =2, 将斜边 AB 绕点 A 顺时针旋转一定角度得到 AD , 过点 D 作 DE ⊥ AC 于点 E , ∠ DAE = ∠ ABC , DE =1, 连接 DO 交☉ O 于点 F. (1) 求证 : AD 是☉ O 的切线 ; (2) 连接 FC 交 AB 于点 G , 连接 FB. 求证 : FG 2 = GO · GB. 图 Z8-17 证明 :(1) ∵☉ O 为 Rt△ ABC 的外接圆 , ∴ O 为斜边 AB 的中点 , AB 为直径 . ∵∠ ACB =90°, ∴∠ ABC + ∠ BAC =90° . ∵∠ DAE = ∠ ABC , ∴∠ DAE + ∠ BAC =90°, ∴∠ BAD =180°-( ∠ DAE + ∠ BAC )=90°, ∴ AD ⊥ AB , ∴ AD 是☉ O 的切线 . 3 . [2019· 兰州 ] 通过对下面数学模型的研究学习 , 解决下面的问题 . 【 模型呈现 】 如图 Z8-15, 在 Rt△ ABC 中 , ∠ ACB =90°, 将斜边 AB 绕点 A 顺时针旋转 90° 得到 AD , 过点 D 作 DE ⊥ AC 于点 E , 可以推理得到 △ ABC ≌△ DAE , 进而得到 AC = DE , BC = AE , 我们把这个数学模型称为 “K 型 ” . 图 Z8-15 推理过程如下 : 图 Z8-16 【 模型应用 】 如图 Z8-17,Rt△ ABC 内接于☉ O , ∠ ACB =90°, BC =2, 将斜边 AB 绕点 A 顺时针旋转一定角度得到 AD , 过点 D 作 DE ⊥ AC 于点 E , ∠ DAE = ∠ ABC , DE =1, 连接 DO 交☉ O 于点 F. (2) 连接 FC 交 AB 于点 G , 连接 FB. 求证 : FG 2 = GO · GB. 图 Z8-17 4 . 如图 Z8-18 ① , 在四边形 ABCD 的边 AB 上任取一点 E ( 点 E 不与 A , B 重合 ), 分别连接 ED , EC. 可以把四边形 ABCD 分成三个三角形 , 如果其中有两个三角形相似 , 我们就把 E 叫做四边形 ABCD 的边 AB 上的 “ 相似点 ”; 如果这三个三角形都相似 , 我们就把 E 叫做四边形 ABCD 的边 AB 上的 “ 强相似点 ” . 【 试题再现 】 如图② , 在 △ ABC 中 , ∠ ACB =90°, 直角顶点 C 在直线 DE 上 , 分别过点 A , B 作 AD ⊥ DE 于点 D , BE ⊥ DE 于点 E. 求证 :△ ADC ∽△ CEB. 图 Z8-18 【 问题探究 】 在图①中 , 若∠ A = ∠ B = ∠ DEC =40°, 试判断点 E 是否是四边形 ABCD 的边 AB 上的相似点 , 并说明理由 . 【 深入探究 】 如图③ , AD ∥ BC , DP 平分∠ ADC , CP 平分∠ BCD 交 DP 于点 P , 过点 P 作 AB ⊥ AD 于点 A , 交 BC 于点 B. (1) 请证明点 P 是四边形 ABCD 的边 AB 上的一个强相似点 ; (2) 若 AD =3, BC =5, 试求 AB 的长 . 图 Z8-18 解 : 【 试题再现 】 证明 : ∵∠ ACB =90°, ∴∠ ACD + ∠ BCE =90°, ∵ AD ⊥ DE , ∴∠ ACD + ∠ CAD =90°, ∴∠ BCE = ∠ CAD , ∵∠ ADC = ∠ CEB =90°, ∴ △ ADC ∽△ CEB. 4 . 如图 Z8-18 ① , 在四边形 ABCD 的边 AB 上任取一点 E ( 点 E 不与 A , B 重合 ), 分别连接 ED , EC. 可以把四边形 ABCD 分成三个三角形 , 如果其中有两个三角形相似 , 我们就把 E 叫做四边形 ABCD 的边 AB 上的 “ 相似点 ”; 如果这三个三角形都相似 , 我们就把 E 叫做四边形 ABCD 的边 AB 上的 “ 强相似点 ” . 【 问题探究 】 在图①中 , 若∠ A = ∠ B = ∠ DEC =40°, 试判断点 E 是否是四边形 ABCD 的边 AB 上的相似点 , 并说明理由 . 图 Z8-18 解 : 【 问题探究 】 点 E 是四边形 ABCD 的边 AB 上的相似点 . 理由如下 : ∵∠ DEC =40°, ∴∠ DEA + ∠ CEB =140°, ∵∠ A =40°, ∴∠ ADE + ∠ AED =140°, ∴∠ ADE = ∠ CEB , ∴ △ ADE ∽△ BEC , ∴点 E 是四边形 ABCD 的边 AB 上的相似点 . 4 . 如图 Z8-18 ① , 在四边形 ABCD 的边 AB 上任取一点 E ( 点 E 不与 A , B 重合 ), 分别连接 ED , EC. 可以把四边形 ABCD 分成三个三角形 , 如果其中有两个三角形相似 , 我们就把 E 叫做四边形 ABCD 的边 AB 上的 “ 相似点 ”; 如果这三个三角形都相似 , 我们就把 E 叫做四边形 ABCD 的边 AB 上的 “ 强相似点 ” . 【 深入探究 】 如图③ , AD ∥ BC , DP 平分∠ ADC , CP 平分∠ BCD 交 DP 于点 P , 过点 P 作 AB ⊥ AD 于点 A , 交 BC 于点 B. (1) 请证明点 P 是四边形 ABCD 的边 AB 上的一个强相似点 ; 图 Z8-18 4 . 如图 Z8-18 ① , 在四边形 ABCD 的边 AB 上任取一点 E ( 点 E 不与 A , B 重合 ), 分别连接 ED , EC. 可以把四边形 ABCD 分成三个三角形 , 如果其中有两个三角形相似 , 我们就把 E 叫做四边形 ABCD 的边 AB 上的 “ 相似点 ”; 如果这三个三角形都相似 , 我们就把 E 叫做四边形 ABCD 的边 AB 上的 “ 强相似点 ” . 【 深入探究 】 如图③ , AD ∥ BC , DP 平分∠ ADC , CP 平分∠ BCD 交 DP 于点 P , 过点 P 作 AB ⊥ AD 于点 A , 交 BC 于点 B. (2) 若 AD =3, BC =5, 试求 AB 的长 . 图 Z8-18 类型四　角含半角模型 例 4 问题:如图Z8-19①,在Rt△ ACB 中,∠ ACB =90°, AC = CB ,∠ DCE =45°,试探究 AD , DE , EB 满足的等量关系 . 【 探究发现 】 小聪同学利用图形变换 , 将 △ CAD 绕点 C 逆时针旋转 90° 得到 △ CBH , 连接 EH , 由已知条件易得∠ EBH =90°, ∠ ECH = ∠ ECB + ∠ BCH = ∠ ECB + ∠ ACD =45° . 根据 “ 边角边 ”, 可证 △ CEH ≌ 　　　　 , 得 EH = ED.  在 Rt△ HBE 中 , 由 　　　 定理 , 可得 BH 2 + EB 2 = EH 2 , 由 BH = AD , 可得 AD , DE , EB 之间的等量关系是 　　　 　 .  图Z8-19 △ CED 勾股 AD 2 + EB 2 = DE 2 【 实践运用 】 (1) 如图② , 在正方形 ABCD 中 ,△ AEF 的顶点 E , F 分别在 BC , CD 边上 , 高 AG 与正方形的边长相等 , 求∠ EAF 的度数 ; (2) 在 (1) 的条件下 , 连接 BD , 分别交 AE , AF 于点 M , N , 若 BE =2, DF =3, BM =, 运用小聪同学探究的结论 , 求正方形的边长及 MN 的长 . 图Z8-19 例 4 问题:如图Z8-19①,在Rt△ ACB 中,∠ ACB =90°, AC = CB ,∠ DCE =45°,试探究 AD , DE , EB 满足的等量关系 . 【 实践运用 】 (1) 如图② , 在正方形 ABCD 中 ,△ AEF 的顶点 E , F 分别在 BC , CD 边上 , 高 AG 与正方形的边长相等 , 求∠ EAF 的度数 ; 图Z8-19 例 4 问题:如图Z8-19①,在Rt△ ACB 中,∠ ACB =90°, AC = CB ,∠ DCE =45°,试探究 AD , DE , EB 满足的等量关系 . 【 实践运用 】 (2) 在 (1) 的条件下 , 连接 BD , 分别交 AE , AF 于点 M , N , 若 BE =2, DF =3, BM =, 运用小聪同学探究的结论 , 求正方形的边长及 MN 的长 . 图Z8-19 【 方法点析 】 1 . 等腰直角三角形角含半角 如图 Z8-20, 在 △ ABC 中 , AB = AC , ∠ BAC =90°, 点 D , E 在 BC 上 , 且∠ DAE =45°, 则 : (1)△ BAE ∽△ ADE ∽△ CDA ; (2) BD 2 + CE 2 = DE 2 . 图 Z8-20 【 拓展 】 (1) 如图 Z8-21, 在 △ ABC 中 , AB = AC , ∠ BAC =90°, 点 D 在 BC 上 , 点 E 在 BC 的延长线上 , 且∠ DAE =45°, 则 BD 2 + CE 2 = DE 2 . 图 Z8-21 可以通过旋转、翻折的方法来证明 , 如图 Z8-22 . 图 Z8-22 图 Z8-23 可以通过旋转、翻折的方法将 BD , DE , EC 转移到一个三角形中 , 如图 Z8-24 . 图 Z8-24 2 . 正方形角含半角 如图 Z8-25, 在正方形 ABCD 中 , 点 E , F 分别在 BC , CD 上 , ∠ EAF =45°, 连接 EF , 则 :   (1) EF = BE + DF ; (2) 如图② , 过点 A 作 AG ⊥ EF 于点 G , 则 AG = AD ; (3) 如图③ , 连接 BD 交 AE 于点 H , 连接 FH , 则 FH ⊥ AE. 图 Z8-25 【 拓展 】 (1) 如图 Z8-26, 在正方形 ABCD 中 , 点 E , F 分别在 CB , DC 的延长线上 , ∠ EAF =45°, 连接 EF , 则 EF = DF - BE. 可以通过旋转的方法来证明 , 如图 Z8-27 . 图 Z8-26 图 Z8-27 图 Z8-28 图 Z8-29 [2013· 达州 ] 通过类比联想、引申拓展研究典型题目 , 可达到解一题知一类的目的 . 下面是一个案例 , 请补充完整 . 原题 : 如图 Z8-30, 点 E , F 分别在正方形 ABCD 的边 BC , CD 上 , ∠ EAF =45°, 连接 EF , 则 EF = BE + DF , 试说明理由 . | 题型精练 | 图 Z8-30 (1) 思路梳理 ∵ AB = AD , ∴把 △ ABE 绕点 A 逆时针旋转 90° 至 △ ADG , 可使 AB 与 AD 重合 . ∵∠ ADC = ∠ B =90°, ∴∠ FDG =180°, 点 F , D , G 共线 . 根据 　　　　 , 易证 △ AFG ≌ 　　　　 , 得 EF = BE + DF.  图 Z8-30 (2) 类比引申 如图② , 四边形 ABCD 中 , AB = AD , ∠ BAD =90° . 点 E , F 分别在边 BC , CD 上 , ∠ EAF = 45° . 若∠ B , ∠ D 都不是直角 , 则当∠ B 与∠ D 满足等量关系 　　　　 时 , 仍有 EF = BE + DF.  图 Z8-30 (3) 联想拓展 如图③ , 在 △ ABC 中 , ∠ BAC =90°, AB = AC , 点 D , E 均在边 BC 上 , 且∠ DAE =45° . 猜想 BD , DE , EC 应满足的等量关系 , 并写出推理过程 . 图 Z8-30 [ 答案 ] (1)SAS 　 △ AFE 　 [2013· 达州 ] 通过类比联想、引申拓展研究典型题目 , 可达到解一题知一类的目的 . 下面是一个案例 , 请补充完整 . 原题 : 如图 Z8-30, 点 E , F 分别在正方形 ABCD 的边 BC , CD 上 , ∠ EAF =45°, 连接 EF , 则 EF = BE + DF , 试说明理由 . 图 Z8-30 (2) 类比引申 如图② , 四边形 ABCD 中 , AB = AD , ∠ BAD =90° . 点 E , F 分别在边 BC , CD 上 , ∠ EAF = 45° . 若∠ B , ∠ D 都不是直角 , 则当∠ B 与∠ D 满足等量关系 　　　　 时 , 仍有 EF = BE + DF.  图 Z8-30 [ 答案 ] (2) ∠ B + ∠ D =180° 　 [2013· 达州 ] 通过类比联想、引申拓展研究典型题目 , 可达到解一题知一类的目的 . 下面是一个案例 , 请补充完整 . 原题 : 如图 Z8-30, 点 E , F 分别在正方形 ABCD 的边 BC , CD 上 , ∠ EAF =45°, 连接 EF , 则 EF = BE + DF , 试说明理由 . 图 Z8-30 (3) 联想拓展 如图③ , 在 △ ABC 中 , ∠ BAC =90°, AB = AC , 点 D , E 均在边 BC 上 , 且∠ DAE =45° . 猜想 BD , DE , EC 应满足的等量关系 , 并写出推理过程 . 图 Z8-30 1 . [2018· 岳阳 ] 已知在 Rt△ ABC 中 , ∠ BAC =90°, CD 为∠ ACB 的平分线 , 将∠ ACB 沿 CD 所在的直线对折 , 使点 B 落在点 B' 处 , 连接 AB' , BB' , 延长 CD 交 BB' 于点 E , 设∠ ABC =2 α (0° <α< 45°) . (1) 如图 Z8-31 ① , 若 AB = AC , 求证 : CD =2 BE ; (2) 如图② , 若 AB ≠ AC , 试求 CD 与 BE 的数量关系 ( 用含 α 的式子表示 ); 综合提升训练 图 Z8-31 图 Z8-31 解 :(1) 证明 : ∵ B , B' 关于 EC 对称 , ∴ BB' ⊥ EC , BE = EB' , ∴∠ DEB = ∠ DAC =90°, ∵∠ EDB = ∠ ADC , ∴∠ DBE = ∠ ACD , ∵ AB = AC , ∠ BAB' = ∠ DAC =90°, ∴ △ BAB' ≌△ CAD , ∴ CD = BB' =2 BE. 1 . [2018· 岳阳 ] 已知在 Rt△ ABC 中 , ∠ BAC =90°, CD 为∠ ACB 的平分线 , 将∠ ACB 沿 CD 所在的直线对折 , 使点 B 落在点 B' 处 , 连接 AB' , BB' , 延长 CD 交 BB' 于点 E , 设∠ ABC =2 α (0° <α< 45°) . (2) 如图② , 若 AB ≠ AC , 试求 CD 与 BE 的数量关系 ( 用含 α 的式子表示 ); 图 Z8-31 图 Z8-31 2 . [2016· 自贡 ] 已知矩形 ABCD 的一条边 AD =8, 将矩形 ABCD 折叠 , 使得顶点 B 落在 CD 边上的 P 点处 . (1) 如图 Z8-32 ① , 已知折痕与边 BC 交于点 O , 连接 AP , OP , OA. 若 △ OCP 与 △ PDA 的面积比为 1 ∶ 4, 求边 CD 的长 . (2) 如图 Z8-32 ② , 在 (1) 的条件下 , 擦去折痕 AO , 线段 OP , 连接 BP. 动点 M 在线段 AP 上 ( 点 M 与点 P , A 不重合 ), 动点 N 在线段 AB 的延长线上 , 且 BN = PM , 连接 MN 交 PB 于点 F , 作 ME ⊥ BP 于点 E. 试问当动点 M , N 在 移动的过程中 , 线段 EF 的长度是否发生 变化 ? 若变化 , 说明变化规律 . 若不变 , 求 出线段 EF 的长度 . 图 Z8-32 2 . [2016· 自贡 ] 已知矩形 ABCD 的一条边 AD =8, 将矩形 ABCD 折叠 , 使得顶点 B 落在 CD 边上的 P 点处 . (2) 如图 Z8-32 ② , 在 (1) 的条件下 , 擦去折痕 AO , 线段 OP , 连接 BP. 动点 M 在线段 AP 上 ( 点 M 与点 P , A 不重合 ), 动点 N 在线段 AB 的延长线上 , 且 BN = PM , 连接 MN 交 PB 于点 F , 作 ME ⊥ BP 于点 E. 试问当动点 M , N 在移动的过程中 , 线段 EF 的长度是否发生 变化 ? 若变化 , 说明变化规律 . 若不变 , 求出线段 EF 的长度 . 图 Z8-32 图 Z8-33 图 Z8-33 图 Z8-33 图 Z8-33 解 :(3) 延长 GP 到点 H , 使得 PH = GP , 连接 CH , DG , DH , 延长 DC 交 EA 的延长线于点 M , 如图③所示 : ∵ GP = PH , ∠ GPF = ∠ HPC , FP = PC , ∴ △ PFG ≌△ PCH , ∴∠ GFC = ∠ HCF , FG = CH , ∴ FG ∥ CH , ∵ FG ∥ AE , ∴ CH ∥ EM , ∴∠ DCH = ∠ M. ∵ CD ∥ AB , ∴∠ M = ∠ MAB , ∴∠ DCH = ∠ MAB , ∵∠ BAD = ∠ AEF =180°-2 α , ∴∠ EAG = ∠ ADC =2 α , ∴∠ GAM =180°-2 α , ∴∠ GAD = ∠ BAM , ∴∠ GAD = ∠ DCH , 4 . [2019· 鄂尔多斯 23 题 ] (1) 【 探究发现 】 如图 Z8-34 ① , ∠ EOF 的顶点 O 在正方形 ABCD 两条对角线的交点处 , ∠ EOF =90°, 将∠ EOF 绕点 O 旋转 , 旋转过程中 , ∠ EOF 的两边分别与正方形 ABCD 的边 BC 和 CD 交于点 E 和点 F ( 点 F 与点 C , D 不重合 ) . 则 CE , CF , BC 之间满足的数量关系是 　　　　 .  图 Z8-34 (2) 【 类比应用 】 如图② , 若将 (1) 中的 “ 正方形 ABCD ” 改为 “ ∠ BCD =120° 的菱形 ABCD ”, 其他条件不变 , 当∠ EOF =60° 时 , 上述结论是否仍然成立 ? 若成立 , 请给出证明 ; 若不成立 , 请猜想结论并说明理由 . 图 Z8-34 图 Z8-34 解 :(1) CE + CF = BC [ 解析 ] ∵四边形 ABCD 是正方形 , ∴ AC ⊥ BD , OB = OC , ∠ OBE = ∠ OCF =45°, ∵∠ EOF = ∠ BOC =90°, ∴∠ BOE = ∠ COF , ∴ △ BOE ≌△ COF (ASA), ∴ BE = CF , ∴ CE + CF = CE + BE = BC. 故答案为 CE + CF = BC. 4 . [2019· 鄂尔多斯 23 题 ] (2) 【 类比应用 】 如图② , 若将 (1) 中的 “ 正方形 ABCD ” 改为 “ ∠ BCD =120° 的菱形 ABCD ”, 其他条件不变 , 当∠ EOF =60° 时 , 上述结论是否仍然成立 ? 若成立 , 请给出证明 ; 若不成立 , 请猜想结论并说明理由 . 图 Z8-34 图 Z8-34 5 . [2017· 临沂 ] 数学课上 , 张老师出示了问题 : 如图 Z8-35 ① , AC , BD 是四边形 ABCD 的对角线 , 若∠ ACB = ∠ ACD = ∠ ABD = ∠ ADB =60°, 则线段 BC , CD , AC 三者之间有何等量关系 ? 经过思考 , 小明展示了一种正确的思路 : 如图② , 延长 CB 到 E , 使 BE = CD , 连接 AE , 证得 △ ABE ≌△ ADC , 从而容易证明 △ ACE 是等边三角形 , 故 AC = CE , 所以 AC = BC + CD. 小亮展示了另一种正确的思路 : 如图③ , 将 △ ABC 绕着点 A 逆时 针旋转 60°, 使 AB 与 AD 重合 , 从 而容易证明 △ ACF 是等边三角 形 , 故 AC = CF , 所以 AC = BC + CD. 在此基础上 , 同学们作了进一步的研究 : 图 Z8-35 (1) 小颖提出 : 如图④ , 如果把 “ ∠ ACB = ∠ ACD = ∠ ABD = ∠ ADB =60°” 改为 “ ∠ ACB = ∠ ACD = ∠ ABD = ∠ ADB =45°”, 其他条件不变 , 那么线段 BC , CD , AC 三者之间有何等量关系 ? 针对小颖提出的问题 , 请你写出结论 , 并给出证明 . (2) 小华提出 : 如图⑤ , 如果把 “ ∠ ACB = ∠ ACD = ∠ ABD = ∠ ADB =60°” 改为 “ ∠ ACB = ∠ ACD = ∠ ABD = ∠ ADB = α ”, 其他条件不变 , 那么线段 BC , CD , AC 三者之间有何等量关系 ? 针对小华提出的问题 , 请你写出结论 , 不用证明 . 图 Z8-35 5 . [2017· 临沂 ] 数学课上 , 张老师出示了问题 : 如图 Z8-35 ① , AC , BD 是四边形 ABCD 的对角线 , 若∠ ACB = ∠ ACD = ∠ ABD = ∠ ADB =60°, 则线段 BC , CD , AC 三者之间有何等量关系 ? 经过思考 , 小明展示了一种正确的思路 : 如图② , 延长 CB 到 E , 使 BE = CD , 连接 AE , 证得 △ ABE ≌△ ADC , 从而容易证明 △ ACE 是等边三角形 , 故 AC = CE , 所以 AC = BC + CD. 小亮展示了另一种正确的思路 : 如图③ , 将 △ ABC 绕着点 A 逆时 针旋转 60°, 使 AB 与 AD 重合 , 从 而容易证明 △ ACF 是等边三角 形 , 故 AC = CF , 所以 AC = BC + CD. 在此基础上 , 同学们作了进一步的研究 : 图 Z8-35 (2) 小华提出 : 如图⑤ , 如果把 “ ∠ ACB = ∠ ACD = ∠ ABD = ∠ ADB =60°” 改为 “ ∠ ACB = ∠ ACD = ∠ ABD = ∠ ADB = α ”, 其他条件不变 , 那么线段 BC , CD , AC 三者之间有何等量关系 ? 针对小华提出的问题 , 请你写出结论 , 不用证明 . 图 Z8-35 6 . [2016· 湖州 ] 数学活动课上 , 某学习小组对有一内角为 120° 的平行四边形 ABCD ( ∠ BAD =120°) 进行探究 : 将一块含 60° 角的直角三角板如图 Z8-36 ①放置在平行四边形 ABCD 所在平面内旋转 , 且 60° 角的顶点始终与点 C 重合 , 较短的直角边和斜边所在的两直线分别交线段 AB , AD 于点 E , F ( 不包括线段的端点 ) . 图 Z8-36 图 Z8-36 6 . [2016· 湖州 ] 数学活动课上 , 某学习小组对有一内角为 120° 的平行四边形 ABCD ( ∠ BAD =120°) 进行探究 : 将一块含 60° 角的直角三角板如图 Z8-36 ①放置在平行四边形 ABCD 所在平面内旋转 , 且 60° 角的顶点始终与点 C 重合 , 较短的直角边和斜边所在的两直线分别交线段 AB , AD 于点 E , F ( 不包括线段的端点 ) . (2) 类比发现 如图② , 若 AD =2 AB , 过点 C 作 CH ⊥ AD 于点 H , 求证 : AE =2 FH ; 图 Z8-36 图 Z8-36 图 Z8-37 (1) 【 类比探究 】 如图 Z8-38, 在▱ ABCD 中 , 点 E , F 分别在 AD , CD 上 , 且 AF = CE , 并相交于点 O , 连接 BE , BF , 求证 : OB 平分∠ AOC. 图 Z8-38 (2) 【 探究延伸 】 如图 Z8-39, 已知直线 m ∥ n , 点 A , C 是直线 m 上两点 , 点 B , D 是直线 n 上两点 , 点 P 是线段 CD 的中点 , 且∠ APB =90°, 两平行线 m , n 间的距离为 4 . 求证 : PA · PB =2 AB. 图 Z8-39 图 Z8-40 图 Z8-37 (2) 【 探究延伸 】 如图 Z8-39, 已知直线 m ∥ n , 点 A , C 是直线 m 上两点 , 点 B , D 是直线 n 上两点 , 点 P 是线段 CD 的中点 , 且∠ APB =90°, 两平行线 m , n 间的距离为 4 . 求证 : PA · PB =2 AB. 图 Z8-39 图 Z8-37 图 Z8-40 8 . [2018· 鄂尔多斯 24 题 ] (1) 【 操作发现 】 如图 Z8-41 ① , 将 △ ABC 绕点 A 顺时针旋转 60° 得到 △ ADE , 连接 BD , 则∠ ABD = 　 度 . (2) 【 类比探究 】 如图② , 在等边三角形 ABC 内任取一点 P , 连接 PA , PB , PC. 求证 : 以 PA , PB , PC 的长为三边必能组成三角形 . 图 Z8-41 ① 图 Z8-41 ② 60 图 Z8-41 ③ (4) 【 拓展应用 】 如图④是 A , B , C 三个村子位置的平面图 , 经测量 AC =4, BC =5, ∠ ACB =30°, P 为 △ ABC 内的一个动点 , 连接 PA , PB , PC. 求 PA + PB + PC 的最小值 . 图 Z8-41 ④ 8 . [2018· 鄂尔多斯 24 题 ] (2) 【 类比探究 】 如图② , 在等边三角形 ABC 内任取一点 P , 连接 PA , PB , PC. 求证 : 以 PA , PB , PC 的长为三边必能组成三角形 . 图 Z8-41 ② 解 : (2) 证明 : 如图 , 将 △ APC 绕点 A 顺时针旋转 60° 得到 △ AQB , 连接 PQ , 则 PC = BQ , AQ = AP , ∠ PAQ =60° . ∴ △ AQP 为等边三角形 . ∴ AP = PQ. ∵ BP , BQ , QP 能组成三角形 , ∴以 PA , PB , PC 的长为三边必能组成三角形 . 图 Z8-41 ③ 8 . [2018· 鄂尔多斯 24 题 ] (4) 【 拓展应用 】 如图④是 A , B , C 三个村子位置的平面图 , 经测量 AC =4, BC =5, ∠ ACB =30°, P 为 △ ABC 内的一个动点 , 连接 PA , PB , PC. 求 PA + PB + PC 的最小值 . 图 Z8-41 ④