2019九年级数学上册 第24章 解直角三角形 24锐角三角函数 4页

‎24.3.1 锐角三角函数 ‎【学习目标】‎ ‎1.掌握锐角三角函数的概念。‎ ‎2.通过学习，培养学生学数学、用数学的意识与能力 ‎【学习重难点】‎ 掌握锐角三角函数的概念 ‎【学习过程】‎ 一、课前准备 如图，已知B1C1⊥AC2，B2C2⊥AC2，求证：＝‎ 二、学习新知 自主学习：‎ 我们曾经使用两种方法求出操场旗杆的高度，其中都出现了两个相似的直角三角形，即 ‎△ABC∽△A′B′C′．‎ 按的比例，就一定有，就是它们的相似比．‎ 当然也有．‎ 我们已经知道，直角三角形ABC可以简记为Rt△ABC，直角∠C所对的边AB称为斜边，用c表示，另两条直角边分别为∠A的对边与邻边，用a、b表示（如图25．2．1）．‎ 前面的结论告诉我们，在Rt△ABC中，只要一个锐角的大小不变（如∠A＝34°），那么不管这个直角三角形大小如何，该锐角的对边与邻边的比值是一个固定的值．‎ 思考 4‎ 一般情况下，在Rt△ABC中，当锐角A取其他固定值时，∠A的对边与邻边的比值还会是一个固定值吗？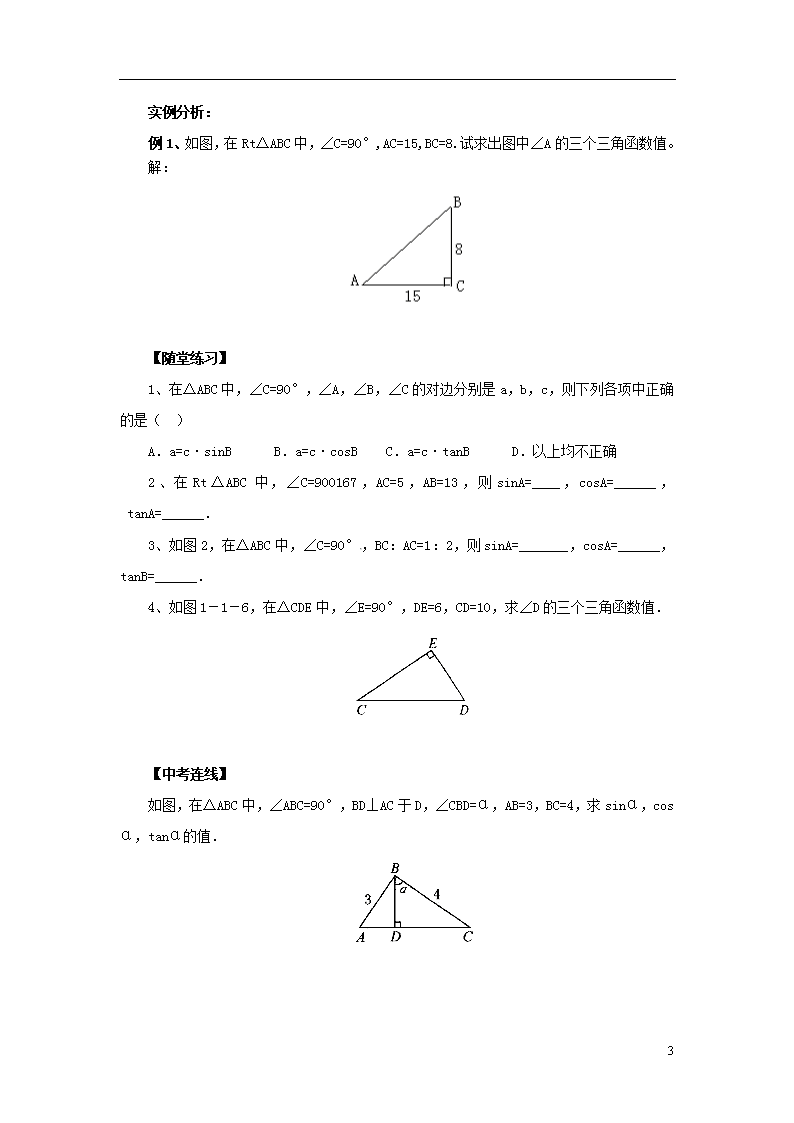‎ 观察图25．2．2中的Rt△、Rt△和Rt△，易知 Rt△∽Rt△_________∽Rt△________，‎ 所以＝_________＝____________．‎ 可见，在Rt△ABC中，对于锐角A的每一个确定的值，其对边与邻边的比值是唯一确定的．‎ 我们同样可以发现，对于锐角A的每一个确定的值，其对边与斜边、邻边与斜边、邻边与对边的比值也是唯一确定的．‎ 因此这几个比值都是锐角A的函数，记作sinA、cosA、tanA，即 sinA＝，cosA＝，‎ tanA＝．‎ 分别叫做锐角∠A的正弦、余弦、正切，统称为锐角∠A的三角函数．‎ 显然，锐角三角函数值都是正实数，并且 ‎0＜sinA＜1，0＜cosA＜1．‎ 根据三角函数的定义，我们还可得出 ‎＝1‎ 4‎ 实例分析：‎ 例1、如图，在Rt△ABC中，∠C=90°,AC=15,BC=8.试求出图中∠A的三个三角函数值。‎ 解：‎ ‎【随堂练习】‎ ‎1、在△ABC中，∠C=90°，∠A，∠B，∠C的对边分别是a，b，c，则下列各项中正确的是（ ）‎ A．a=c·sinB B．a=c·cosB C．a=c·tanB D．以上均不正确 ‎2、在Rt△ABC中，∠C=900167，AC=5，AB=13，则sinA=____，cosA=______，tanA=______．‎ ‎3、如图2，在△ABC中，∠C=90°，BC：AC=1：2，则sinA=_______，cosA=______，tanB=______．‎ ‎4、如图1－1－6，在△CDE中，∠E=90°，DE=6，CD=10，求∠D的三个三角函数值．‎ ‎【中考连线】‎ 如图，在△ABC中，∠ABC=90°，BD⊥AC于D，∠CBD=α，AB=3，BC=4，求sinα，cosα，tanα的值．‎ 4‎ ‎【参考答案】‎ 随堂练习 ‎ 1、B 2、，， 3、，，2 4、sinD=，cosD=，tanD=‎ 中考连线 sinα=，cosα=，tanα= ‎ 4‎