鄂尔多斯专版2020中考数学复习方案第四单元三角形第16课时三角形及其性质课件 34页

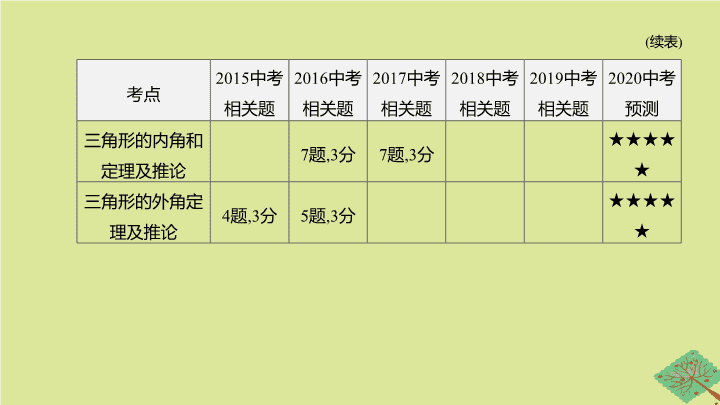
第 16 课时 三角形及其性质 第四单元　三角形 【 考情分析 】 考点 2015 中考 相关题 2016 中考 相关题 2017 中考 相关题 2018 中考 相关题 2019 中考 相关题 2020 中考预测 三角形的概 念及分类 ★★ 三角形中的 重要线段 6 题 ,3 分 14 题 ,3 分 21 题 ,9 分 24 题 ,12 分 16 题 ,3 分 ★★★★★ 三角形的三边关系 9 题 ,3 分 ★★★ 考点 2015 中考 相关题 2016 中考 相关题 2017 中考 相关题 2018 中考 相关题 2019 中考 相关题 2020 中考预测 三角形的内角和 定理及推论 7 题 ,3 分 7 题 ,3 分 ★★★★★ 三角形的外角定 理及推论 4 题 ,3 分 5 题 ,3 分 ★★★★★ ( 续表 ) 考点一　三角形的分类 考点聚焦 考点二　三角形边和角的性质 1 . 三边关系 : 三角形两边之和 ① 　　　 第三边 , 两边之差 ② 　　　 第三边 .  大于 小于 【 温馨提示 】 判断给定的三条线段能否组成三角形 , 只要判断两条较短线段的和是否大于最长线段即可 . 2 . 三角形内角、外角 (1) 内角和定理 : 三角形三个内角的和等于 ③ 　　 　 .  (2) 内外角关系 :a . 三角形的外角等于与它不相邻的两个内角的 ④ 　　　　 ;  b . 三角形的一个外角大于任何一个与它不相邻的内角 . 3 . 边角关系 : 在同一个三角形中 , 等边对等角 , 等角对等边 , 大边对大角 , 小边对小角 . 180° 和 考点三　与三角形有关的重要线段或直线 名称 图形 性质 重要结论 中 线 　 BD = ⑤ 　　　 = ⑥ 　　　 BC  　 三角形的三条中线的交点在三角形的 ⑦ 　　　 部 , 中线将三角形分成两个面积相等的三角形   角 平 分 线 　 三角形的三条角平分线的交点在三角形的 ⑨ 　　　 部 , 这个点称为内心   DC 内 ∠2 内 名称 图形 性质 重要结论 高 线 　 AD ⊥ ⑩ 　 　 , 即 ∠ ADB = ⑪ 　 = 90 °  ⑫ 　　　　 三角形的三条高的交点在三角形的内部 ; ⑬ 　　　　 三角形的三条高的交点是直角顶点 ; ⑭ 　　　　 三角形的三条高所在直线的交点 在三角形 的外部 , 这个点称为 垂心 ( 续表 ) 锐角 BC ∠ ADC 直角 钝角 名称 图形 性质 重要结论 中 位 线 ⑮ 　 ∥ BC 且 DE = ⑯ 　 　 BC  　 中位线所截得的三角形与原三角形相似 , 其相似比为 1 ∶ 2, 面积比为 1 ∶ 4 ( 续表 ) DE 题组一　必会题 对点演练 1 . 下列长度的三根小木棒能构成三角形的是 ( 　　 ) A . 2 cm,3 cm,5 cm B . 7 cm,4 cm,2 cm C . 3 cm,4 cm,8 cm D . 3 cm,3 cm,4 cm D 2 . 在 △ ABC 中 , 已知∠ A =40°, ∠ B =50°, 则此三角形是 ( 　　 ) A . 锐角三角形 B . 直角三角形 C . 钝角三角形 D . 无法判断 B 3 . [2018· 广西 ] 如图 16-1, ∠ ACD 是 △ ABC 的外角 , CE 平分∠ ACD , 若∠ A =60°, ∠ B = 40°, 则∠ ECD 等于 ( 　　 ) A . 40° B . 45° C . 50° D . 55° C 图 16-1 题组二　易错题 【 失分点 】 忽视三角形三边关系的特殊性 ; 不能正确地判断三角形中的重要线段 . 4 . 下列四个图形中 , 线段 BE 是 △ ABC 的高的是 ( 　　 )   图 16-2 D 5 . [2018· 泰州 ] 已知三角形两边的长分别为 1,5, 第三边长为整数 , 则第三边的长为 　　　　 .  [ 答案 ] 5 　 [ 解析 ] 根据三角形的三边关系 , 得 6 > 第三边的长 > 4 . 因为第三条边的长为整数 , 所以第三边的长是 5 . 6 . 从 △ ABC 顶点 A 作高线 AD 和角平分线 AE , 若 AD 与 AE 的夹角为 15°, 且∠ B =50°, 则∠ C = 　　　　 .  [ 答案 ] 20° 或 80° 　 [ 解析 ] 当∠ B> ∠ C 时 , 如图① , ∵ AD ⊥ BC , ∴∠ ADB =90° . ∵∠ B =50°, ∴∠ BAD =40° . ∵∠ DAE =15°, ∴∠ BAE =55°, ∴∠ BAC =110°, ∴∠ C =180°- ∠ B - ∠ BAC =180°-50°-110°=20° . 当∠ B< ∠ C 时 , 如图② , ∵ AD ⊥ BC , ∴∠ ADB =90°, ∵∠ B =50°, ∴∠ BAD =40°, ∵∠ DAE =15°, ∴∠ BAE = ∠ EAC =25°, ∴∠ DAC =10°, ∴∠ C =90°- ∠ DAC =80° . 综上所述 , ∠ C =20° 或 80° . 考向一　三角形三边的关系 例 1 现有 3 cm,4 cm,7 cm,9 cm 长的四根木棒 , 任取其中三根组成一个三角形 , 那么可以组成的三角形的个数是 ( 　　 ) A . 1 B . 2 C . 3 D . 4 [ 答案 ] B 　 [ 解析 ] 四根木棒的所有组合 :3 cm, 4 cm,7 cm 和 3 cm,4 cm,9 cm 和 3 cm, 7 cm,9 cm 和 4 cm,7 cm,9 cm, 只有长度分别为 3 cm,7 cm,9 cm 和 4 cm,7 cm,9 cm 的三根能组成三角形 . 故选 B . | 考向精练 | 1 . [2019· 金华 ] 若长度分别为 a ,3,5 的三条线段能组成一个三角形 , 则 a 的值可以是 ( 　　 ) A . 1 B . 2 C . 3 D . 8 C 2 . [2019· 扬州 ] 已知 n 是正整数 , 若一个三角形的三边长分别是 n +2, n +8,3 n , 则满足条件的 n 的值有 ( 　　 ) A . 4 个 B . 5 个 C . 6 个 D . 7 个 [ 答案 ] D 　 考向二　三角形内角与外角的运用 例 2 (1) 在 △ ABC 中 , ∠ ABC , ∠ ACB 的平分线 BE , CD 相交于点 F , ∠ ABC =42°, ∠ A = 60°, 则∠ BFC = 　　　　 .  (2) 在 △ ABC 中 , ∠ ABC 的平分线 BE 与∠ ACB 的外角平分线 CD 相交于点 F , ∠ ABC = 42°, ∠ A =60°, 则∠ BFC = 　　　　 .  (3) 在 △ ABC 中 , ∠ ABC 的外角平分线 BE 与∠ ACB 的外角平分线 CD 相交于点 F , ∠ ABC =42°, ∠ A =60°, 则∠ BFC = 　　　　 .  [ 答案 ] (1)120° 例 2 (2) 在 △ ABC 中 , ∠ ABC 的平分线 BE 与∠ ACB 的外角平分线 CD 相交于点 F , ∠ ABC =42°, ∠ A =60°, 则∠ BFC = 　　　　 .  [ 答案 ] (2)30° 例 2 (3) 在 △ ABC 中 , ∠ ABC 的外角平分线 BE 与∠ ACB 的外角平分线 CD 相交于点 F , ∠ ABC =42°, ∠ A =60°, 则∠ BFC = 　　　　 .  [ 答案 ] (3)60° 【 方法点析 】 求较复杂图形中的角度时 , 经常把需要求的角度与已知角度通过等量代换等方法转化为同一个三角形的内角或外角 , 再利用三角形的内角和定理及推论解决问题 . | 考向精练 | 1 . [2019· 凉山州 ] 如图 16-3, BD ∥ EF , AE 与 BD 交于点 C , ∠ B =30°, ∠ A =75°, 则∠ E 的度数为 ( 　　 ) A . 135° B . 125° C . 115° D . 105° 图 16-3 [ 答案 ] D 　 [ 解析 ] ∵∠ ACD = ∠ A + ∠ B =30°+75°=105°, BD ∥ EF , ∴∠ E = ∠ ACD =105°, 故选 D . 2 . [2018· 昆明 ] 在 △ AOC 中 , OB 交 AC 于点 D , 量角器的摆放如图 16-4, 则∠ CDO 的度数为 ( 　　 ) A . 90° B . 95° C . 100° D . 120° [ 答案 ] B 　 [ 解析 ] ∵ CO = AO , ∠ AOC =130°, ∴∠ CAO =25° . 又∵∠ AOB =70°, ∴∠ CDO = ∠ CAO + ∠ AOB =25°+70°=95° . 故选 B . 图 16-4 考向三　三角形中的重要线段 例 3 如图 16-5, 在 △ ABC 中 , AB =5, AC =3, AD , AE 分别为 △ ABC 的中线和角平分线 , 过点 C 作 CH ⊥ AE 于点 H , 并延长交 AB 于点 F , 连接 DH , 则线段 DH 的长为 　　　 .  图 16-5 [ 答案 ] 1 | 考向精练 | 1 . [2019· 长沙 ] 如图 16-6, 要测量池塘两岸相对的 A , B 两点间的距离 , 可以在池塘外选一点 C , 连接 AC , BC , 分别取 AC , BC 的中点 D , E , 测得 DE =50 m, 则 AB 的长是 　　　　 m .  图 16-6 100 2 . [2018· 黄石 ] 如图 16-7, 在 △ ABC 中 , AD 是 BC 边上的高 , AE , BF 分别是∠ BAC , ∠ ABC 的平分线 , ∠ BAC =50°, ∠ ABC =60°, 则∠ EAD + ∠ ACD = ( 　　 ) A . 75° 　　　　　 B . 80° C . 85° 　　　　　 D . 90° 图 16-7 [ 答案 ] A 　 [ 解析 ] ∵ AD 是 BC 边上的高 , ∠ ABC =60°, ∴∠ BAD =30° . ∵∠ BAC =50°, AE 平分∠ BAC , ∴∠ BAE =25°, ∴∠ DAE =30°-25°=5° . ∵在 △ ABC 中 , ∠ C =180°- ∠ ABC - ∠ BAC =70°, ∴∠ EAD + ∠ ACD =5°+70°=75° . 故选 A .