2020年中考物理总复习尖子生必刷题特训07计算题20题含解析 20页

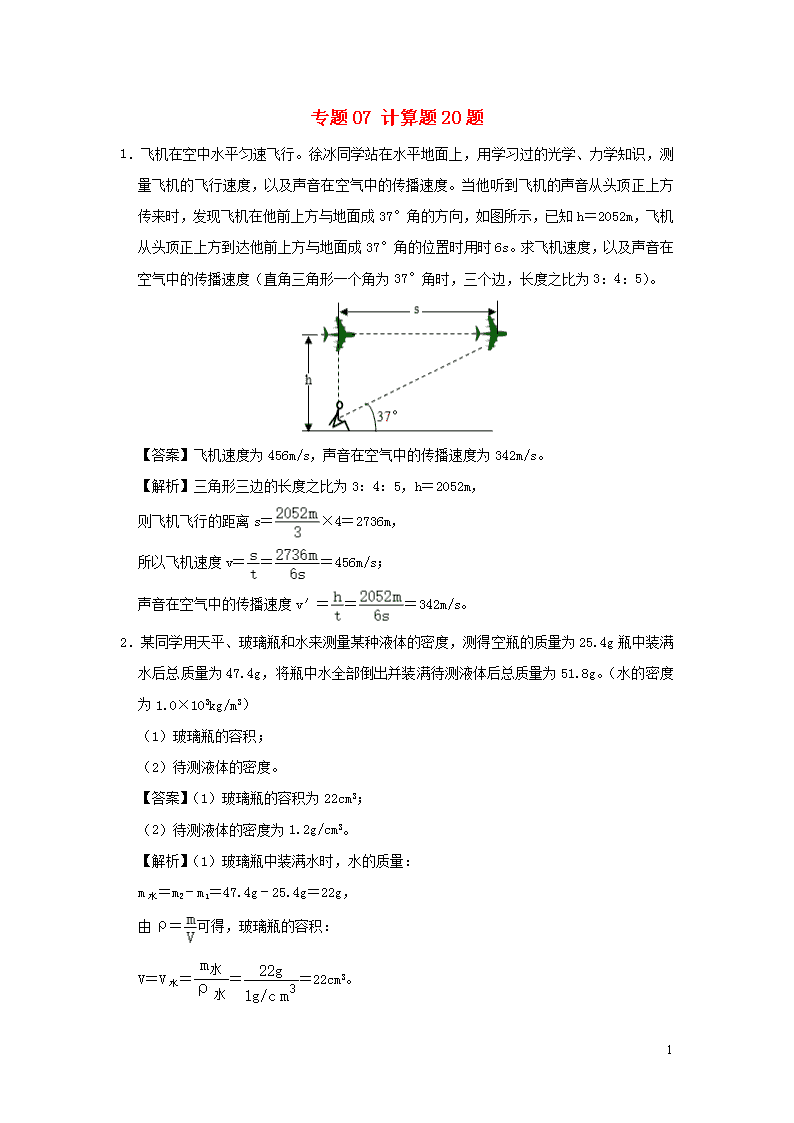
专题07 计算题20题 ‎1．飞机在空中水平匀速飞行。徐冰同学站在水平地面上，用学习过的光学、力学知识，测量飞机的飞行速度，以及声音在空气中的传播速度。当他听到飞机的声音从头顶正上方传来时，发现飞机在他前上方与地面成37°角的方向，如图所示，已知h＝2052m，飞机从头顶正上方到达他前上方与地面成37°角的位置时用时6s。求飞机速度，以及声音在空气中的传播速度（直角三角形一个角为37°角时，三个边，长度之比为3：4：5）。‎ ‎【答案】飞机速度为456m/s，声音在空气中的传播速度为342m/s。‎ ‎【解析】三角形三边的长度之比为3：4：5，h＝2052m，‎ 则飞机飞行的距离s＝×4＝2736m，‎ 所以飞机速度v＝＝＝456m/s；‎ 声音在空气中的传播速度v′＝＝＝342m/s。‎ ‎2．某同学用天平、玻璃瓶和水来测量某种液体的密度，测得空瓶的质量为25.4g瓶中装满水后总质量为47.4g，将瓶中水全部倒出并装满待测液体后总质量为51.8g。（水的密度为1.0×103kg/m3）‎ ‎（1）玻璃瓶的容积；‎ ‎（2）待测液体的密度。‎ ‎【答案】（1）玻璃瓶的容积为22cm3；‎ ‎（2）待测液体的密度为1.2g/cm3。‎ ‎【解析】（1）玻璃瓶中装满水时，水的质量：‎ m水＝m2﹣m1＝47.4g﹣25.4g＝22g，‎ 由ρ＝可得，玻璃瓶的容积：‎ V＝V水＝＝＝22cm3。‎ 20‎ ‎（2）玻璃瓶中装满待测液体时，待测液体的质量：‎ m液＝m3﹣m1＝51.8g﹣25.4g＝26.4g，‎ 待测液体的体积：‎ V液＝V瓶＝22cm3，‎ 待测液体的密度：‎ ρ液＝＝＝1.2g/cm3。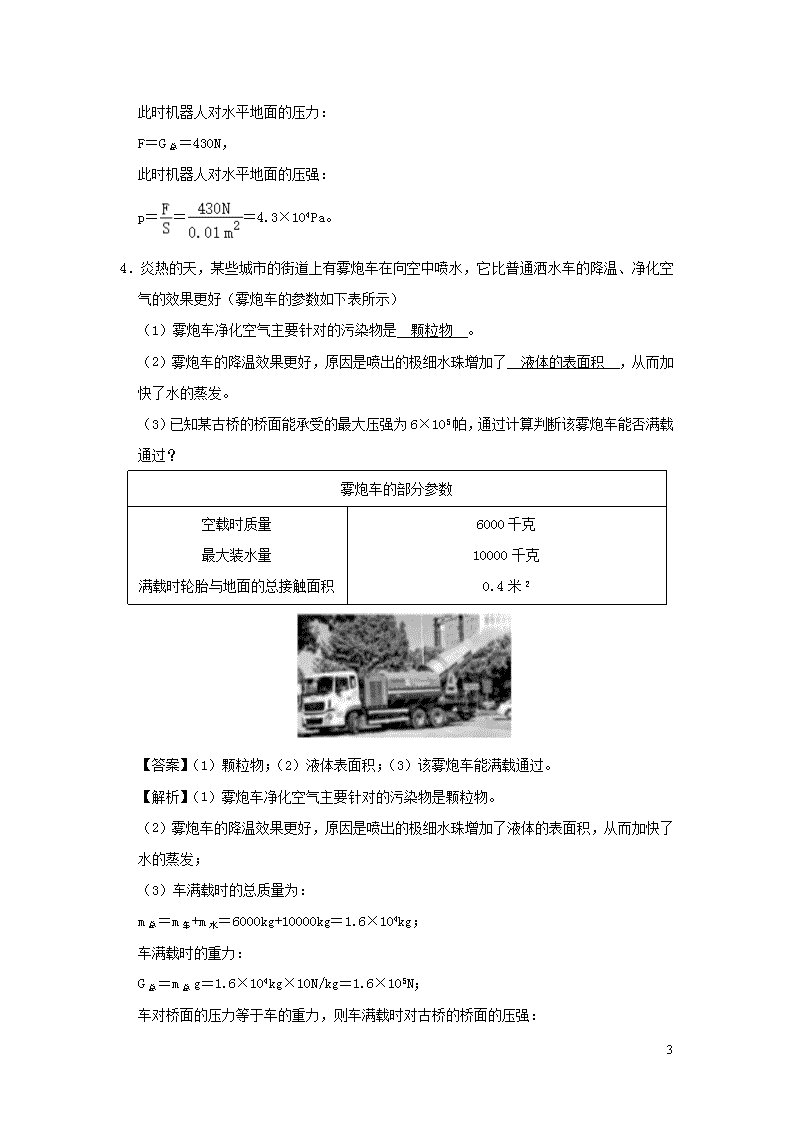‎ ‎3．人工智能逐渐融入我们的生活。如图所示，某餐厅的送餐机器人的质量为40kg，它与地面的接触面积为0.01m2。‎ ‎（1）求送餐机器人的重力；‎ ‎（2）送餐机器人的外壳是由玻璃钢材料制作的。有一小块玻璃钢材料的质量为90g，体积为50cm3，求该材料的密度；‎ ‎（3）若送餐机器人托着3kg的物体，求此时机器人对水平地面的压强。‎ ‎【答案】（1）送餐机器人的重力为400N；‎ ‎（2）该材料的密度为1.8g/cm3；‎ ‎（3）此时机器人对水平地面的压强为4.3×104Pa。‎ ‎【解析】（1）送餐机器人的重力：‎ G＝mg＝40kg×10N/kg＝400N；‎ ‎（2）该材料的密度：‎ ρ＝＝＝1.8g/cm3；‎ ‎（3）送餐机器人托着3kg的物体，总质量：‎ m总＝3kg+40kg＝43kg，‎ 总重力：‎ G总＝m总g＝43kg×10N/kg＝430N，‎ 20‎ 此时机器人对水平地面的压力：‎ F＝G总＝430N，‎ 此时机器人对水平地面的压强：‎ p＝＝＝4.3×104Pa。‎ ‎4．炎热的天，某些城市的街道上有雾炮车在向空中喷水，它比普通洒水车的降温、净化空气的效果更好（雾炮车的参数如下表所示）‎ ‎（1）雾炮车净化空气主要针对的污染物是　颗粒物　。‎ ‎（2）雾炮车的降温效果更好，原因是喷出的极细水珠增加了　液体的表面积　，从而加快了水的蒸发。‎ ‎（3）已知某古桥的桥面能承受的最大压强为6×105帕，通过计算判断该雾炮车能否满载通过？‎ 雾炮车的部分参数 空载时质量 最大装水量 满载时轮胎与地面的总接触面积 ‎6000千克 ‎10000千克 ‎0.4米2‎ ‎【答案】（1）颗粒物；（2）液体表面积；（3）该雾炮车能满载通过。‎ ‎【解析】（1）雾炮车净化空气主要针对的污染物是颗粒物。‎ ‎（2）雾炮车的降温效果更好，原因是喷出的极细水珠增加了液体的表面积，从而加快了水的蒸发；‎ ‎（3）车满载时的总质量为：‎ m总＝m车+m水＝6000kg+10000kg＝1.6×104kg；‎ 车满载时的重力：‎ G总＝m总g＝1.6×104kg×10N/kg＝1.6×105N；‎ 车对桥面的压力等于车的重力，则车满载时对古桥的桥面的压强：‎ 20‎ p＝＝＝4×105Pa＜6×105Pa。‎ 故该雾炮车能满载通过。‎ ‎5．2019年，我国航天事业取得了世界瞩目的又一项成就﹣“玉兔二号”月球车成功 登陆月球背面。图示为科技馆展厅内“玉兔二号”月球车的模型，质量为36kg。‎ ‎（1）模型车静止在水平地面上时，它对地面的压力为多少牛？（g取10N/kg）‎ ‎（2）若车轮与地面的总接触面积为400cm2，则车对地面的压强为多少帕？‎ ‎【答案】（1）模型车静止在水平地面上时，它对地面的压力为360N；‎ ‎（2）若车轮与地面的总接触面积为400cm2，则车对地面的压强9×103Pa。‎ ‎【解析】（1）模型车静止在水平地面上时，它对地面的压力：‎ F＝G＝mg＝36kg×10N/kg＝360N。‎ ‎（2）车对地面的压强：‎ p＝＝＝9×103Pa。‎ ‎6．如图甲所示，均匀圆柱体A和薄璧圆柱形容器B置于水平地面上。容器B的底面积为2×10﹣2m2，其内部盛有0.2m深的水，g＝10N/kg。求：‎ ‎（1）容器中水的重力。‎ ‎（2）水对容器底部的压强。‎ ‎（3）现将A浸没在容器B的水中（水未溢出），如图乙所示。水对容器底部压强的增加量为1000Pa，容器B对水平地面压强的增加量为1500Pa．求A静止后在水中受到的浮力和容器底部对它的支持力。‎ ‎【答案】（1）容器中水的重力为40N；‎ 20‎ ‎（2）水对容器底部的压强为2000Pa；‎ ‎（3）A静止后在水中受到的浮力为20N，容器底部对它的支持力为10N。‎ ‎【解析】（1）容器内水的体积：‎ V水＝S容h水＝2×10﹣2m2×0.2m＝4×10﹣3m3，‎ 由ρ＝可得，容器中水的质量：‎ m水＝ρ水V水＝1.0×103kg/m3×4×10﹣3m3＝4kg，‎ 则容器中水的重力：‎ G水＝m水g＝4kg×10N/kg＝40N；‎ ‎（2）水对容器底部的压强：‎ p水＝ρ水gh水＝1.0×103kg/m3×10N/kg×0.2m＝2000Pa；‎ ‎（3）将A浸没在容器B的水中时，水面上升的高度：‎ ‎△h＝＝＝0.1m，‎ 则A排开水的体积：‎ V排＝S容△h＝2×10﹣2m2×0.1m＝2×10﹣3m3，‎ A静止后在水中受到的浮力：‎ F浮＝ρ水gV排＝1.0×103kg/m3×10N/kg×2×10﹣3m3＝20N；‎ 因水平面上物体的压力和自身的重力相等，‎ 所以，由p＝可得，容器对地面压力的增加量即A的重力：‎ GA＝△F容＝△p容S容＝1500Pa×2×10﹣2m2＝30N，‎ 又因A受到竖直向上的支持力、浮力和竖直向下的重力作用而处于平衡状态，‎ 所以，容器底部对A的支持力：‎ F支＝GA﹣F浮＝30N﹣20N＝10N。‎ ‎7．如图甲所示，拉力F通过滑轮组，将正方体金属块从水中匀速拉出至水面上方一定高度处。图乙是拉力F随时间t变化的关系图象。不计动滑轮的重力、摩擦及水和空气对金属块的阻力，g＝10N/kg，求：‎ ‎（1）金属块完全浸没在水中时受到的浮力大小；‎ ‎（2）金属块的密度；‎ ‎（3）如果直接将金属块平放在水平地面上，它对地面的压强大小。‎ 20‎ ‎【答案】（1）金属块完全浸没在水中时受到的浮力80N；‎ ‎（2）金属块的密度2.7×103kg/m3；‎ ‎（3）如果直接将金属块平放在水平地面上，它对地面的压强5.4×103Pa。‎ ‎【解析】（1）由甲图可知，n＝2，不计动滑轮的重力、摩擦及水和空气对金属块的阻力，F＝G，‎ 当金属块完全露出液面后，金属块不受浮力，此时拉力等于重力，即为图中的t2﹣t3时刻，‎ 从乙图可知，该金属块重力为：G＝2F＝2×108N＝216N，‎ 当金属块未露出液面时，即为图中的0﹣t1时刻，‎ 则2F′+F浮＝G，‎ 所以金属块完全浸没在水中时受到的浮力：F浮＝G﹣2F′＝216N﹣2×68N＝80N；‎ ‎（2）根据F浮＝ρgV排可得，金属块排开水的体积：V排＝＝＝8×10﹣3m3，‎ 金属块完全浸没在水中，则金属块的体积V＝V排＝8×10﹣3m3，‎ 则根据G＝mg、ρ＝可得，金属块的密度为：ρ金＝＝＝2.7×103kg/m3。‎ ‎（3）金属块的边长a＝＝＝0.2m，‎ 20‎ 则受力面积S＝a2＝（0.2m）2＝0.04m2，‎ 金属块平放在水平地面时对地面的压强：p＝＝＝＝5.4×103Pa。‎ ‎8．用弹簧测力计悬挂一实心物块，物块下表面与水面刚好接触，如图甲所示。由此处匀速下放物块，直至浸没于水中并继续匀速下放（物块始终未与容器接触）。物块下放过程中，弹簧测力计示数F与物块下表面浸入水中的深度h的关系如图乙所示。求：‎ ‎（1）物块完全浸没在水中受到的浮力；‎ ‎（2）物块的密度；‎ ‎（3）从物块刚好浸没水中到h＝10cm过程中，水对物块下表面的压强变化了多少Pa？‎ ‎【答案】（1）物块完全浸没在水中受到的浮力为4N；‎ ‎（2）物块的密度2×103kg/m3；‎ ‎（3）从物块刚好浸没水中到h＝10cm过程中，水对物块下表面的压强变化了600Pa。‎ ‎【解析】（1）由图象可知，弹簧测力计的最大示数F最大＝8N，此时物块未浸入水中，则物块重力G＝F最大＝8N；‎ 物块全浸入时弹簧测力计的示数F示＝4N，‎ 受到的浮力：‎ F浮＝G﹣F示＝8N﹣4N＝4N；‎ ‎（2）由F浮＝ρ水gV排得物块的体积：‎ V＝V排＝＝＝4×10﹣4m3，‎ 物块的质量：‎ m＝＝＝0.8kg，‎ 20‎ ρ物＝＝＝2×103kg/m3；‎ ‎（3）由图乙可知，h1＝4cm时物块刚好浸没水中，从物块刚好浸没水中到h2＝10cm过程中，‎ 物块下表面变化的深度△h＝h2﹣h1＝10cm﹣4cm＝6cm＝0.06m，‎ 水对物块下表面的压强变化：‎ ‎△p＝ρ水g△h＝1×103kg/m3×10N/kg×0.06m＝600Pa。‎ ‎9．某容器放在水平桌面上，盛有足量的水。现将体积为1.25×10﹣4m3、质量为0.4kg的实心正方体放入水中，正方体不断下沉，直到沉底，如图所示。（已知ρ水＝1.0×103kg/m3，g＝10N/kg）求：‎ ‎（1）正方体受到的重力的大小；‎ ‎（2）正方体浸没在水中受到的浮力的大小F浮；‎ ‎（3）容器底部对正方体的支持力的大小和正方体对容器底部的压强。‎ ‎【答案】（1）正方体受到的重力的大小为4N；‎ ‎（2）正方体浸没在水中受到的浮力的大小F浮＝1.25N；‎ ‎（3）容器底部对正方体的支持力的大小为2.75N，正方体对容器底部的压强为1.1×103Pa。‎ ‎【解析】（1）正方体的重力G＝mg＝0.4kg×10N/kg＝4N；‎ ‎（2）正方体浸没在水中，V排＝V＝1.25×10﹣4m3，‎ 则F浮＝ρ水gV排＝1.0×103kg/m3×10N/kg×1.25×10﹣4m3＝1.25N；‎ ‎（3）正方体沉在底部，由于处于静止状态，则受力平衡，即G＝N+F浮，‎ 所以，N＝G﹣F浮＝4N﹣1.25N＝2.75N；‎ 由于支持力与压力是一对相互作用力，则可知正方体对容器底部的压力F＝N＝2.75N，‎ 正方体的边长L＝＝＝0.05m，‎ 则正方体对容器底部的压强p＝＝＝1.1×103Pa。‎ 20‎ ‎10．如图所示，质量为2.5t的汽车在平直的公路上匀速行驶，在其前方有一固定的测速仪向汽车发出两次短促的超声波信号，第一次发出信号到接收到信号用时0.6s，第二次发出信号到接收到信号用时0.4s，测出汽车的速度为34m/s。已知汽车在公路上匀速行驶时受到的阻力是车重的0.02倍，超声波的速度为340m/s。（g取10N/kg）求：‎ ‎（1）汽车匀速行驶时受到的牵引力；‎ ‎（2）汽车匀速行驶10s内牵引力做的功；‎ ‎（3）测速仪两次发出信号的时间间隔。‎ ‎【答案】（1）汽车匀速行驶时受到的牵引力500N；‎ ‎（2）汽车匀速行驶10s内牵引力做的功1.7×105J；‎ ‎（3）测速仪两次发出信号的时间间隔1.1s。‎ ‎【解析】（1）汽车的重力：G＝mg＝2.5×103kg×10N/kg＝2.5×104N 汽车受到的阻力：F阻＝0.02G＝0.02×2.5×104N＝500N 汽车匀速直线行驶时，汽车受到的阻力和牵引力是平衡力：F＝F阻＝500N ‎（2）汽车10s内行驶的距离：s＝v车t＝34m/s×10s＝340m 牵引力做功：W＝Fs＝500N×340m＝1.7×105J ‎（3）由v＝得：汽车接收到第一次信号时，汽车距测速仪：s1＝v声t1＝340m/s×＝102m 则汽车接收到第二次信号时，汽车距测速仪：s2＝v声t2＝340m/s×＝68m 因此汽车在两次信号的间隔过程中行驶：s′＝s1﹣s2＝102m﹣68m＝34m 设测速器发出两次信号时间差为△t，汽车行驶34m共用时间：t′＝△t﹣t1+t2＝△t﹣+＝△t﹣0.1s 汽车的车速：v′＝＝＝34m/s 解得测速仪两次发出信号的时间间隔：△t＝1.1s ‎11．如图，为迎宾路高架桥的部分路段示意图，水平路面AB＝200m、斜坡BC＝120m、坡高CD＝6m。搭载乘客后总重为G＝1.5×105N的公交车，轮胎与水平路面总接触面积为0.4m2．当它以恒定功率P1匀速通过AB段时，用时t1＝20s；以恒定功率P2匀速通过BC 20‎ 段时，用时t2＝16s。公交车在AB段和BC段行驶时受到的阻力始终是车总重的0.01倍。请完成下列问题：‎ ‎（1）求出公交车静止在水平地面时对地面的压强，以及通过BC段时的速度。‎ ‎（2）公交车通过AB段时，牵引力的功率P1是多少瓦特？‎ ‎（3）公交车通过BC段时，牵引力的大小为多少牛顿？‎ ‎【答案】（1）公交车静止在水平地面时对地面的压强为3.75×105Pa；通过BC段时的速度为7.5m/s；‎ ‎（2）公交车通过AB段时，牵引力的功率P为1.5×104W；‎ ‎（3）公交车通过BC段时，牵引力的大小为9×103N。‎ ‎【解析】（1）公交车静止在水平地面时对地面的压力F＝G＝1.5×105N，已知轮胎与水平路面总接触面积S＝0.4m2。‎ 公交车静止在水平地面时对地面的压强：‎ p＝＝＝3.75×105Pa；‎ BC段时的速度vBC＝＝＝7.5m/s；‎ ‎（2）AB段时的速度vAB＝＝＝10m/s；‎ 公交车在AB段行驶时受到的阻力f＝0.01G＝0.01×1.5×105N＝1.5×103N，‎ 因为匀速行驶，所以牵引力F1＝F2＝f＝1.5×103N，‎ 则牵引力F1的功率：‎ P1＝＝＝F1vAB＝1.5×103N×10m/s＝1.5×104W；‎ 牵引力F2的功率：P2＝＝＝F2vBC＝1.5×103N×7.5m/s＝1.125×104W；‎ ‎（3）由题知，公交车在AB段和BC段行驶时受到的阻力相等，‎ 公交车通过BC段时，克服阻力做的额外功：‎ W额外＝fSBC＝1.5×103N×120m＝1.8×105J；‎ 克服重力做的有用功：‎ 20‎ W有用＝GhCD＝1.5×105N×6m＝9×105J；‎ 公交车通过BC段时牵引力做的功：‎ WBC＝W有用+W额外＝9×105J+1.8×105J＝1.08×106J。‎ 由W＝Fs可得，‎ 牵引力F＝＝＝9×103N；‎ ‎12．如图所示，在水平路面上行驶的汽车通过滑轮组拉着重G＝9×104N的货物A沿斜面向上匀速运动。货物A的速度为v＝2m/s，经过t＝10s，货物A竖直升高h＝10m。已知汽车对绳的拉力F的功率P＝120kW，不计绳、滑轮的质量和摩擦，求：‎ ‎（1）t时间内汽车对绳的拉力所做的功；‎ ‎（2）汽车对绳的拉力大小；‎ ‎（3）斜面的机械效率。‎ ‎【答案】（1）t时间内汽车对绳的拉力所做的功为1.2×106J；‎ ‎（2）汽车对绳的拉力大小为20000N；‎ ‎（3）斜面的机械效率为75%。‎ ‎【解析】（1）由P＝可得t时间内汽车对绳的拉力所做的功：‎ W＝Pt＝1.2×105W×10s＝1.2×106J；‎ ‎（2）10s内货物移动的距离：s物＝vt＝2m/s×10s＝20m，‎ 由图知，n＝3，拉力端移动距离：s＝3s物＝3×20m＝60m，‎ 由W＝Fs可得汽车对绳的拉力大小：‎ F＝＝＝20000N；‎ ‎（3）不计绳、滑轮的质量和摩擦，滑轮组对重物的拉力：‎ F拉＝3F＝3×20000N＝60000N，‎ 斜面的机械效率：‎ 20‎ η＝＝＝×100%＝75%。‎ ‎13．在一次车辆故障处置过程中，拖车所用装置简化为如图所示的滑轮组。为了尽快疏通道路，交警指挥拖车只用了30s时间，将水平路面上质量是1.5t的故障车匀速拖离了现场。若故障车被拖离的速度是5m/s，绳子自由端的拉力F是500N，地面对故障车的摩擦力为车重力的0.08倍。求：‎ ‎（1）拉力F在30s内所做的功；‎ ‎（2）整个装置的机械效率。‎ ‎【答案】（1）拉力F在30s内所做的功为2.25×105J；‎ ‎（2）整个装置的机械效率为80%。‎ ‎【解析】（1）由v＝可得故障车在30s内通过的路程：‎ s车＝v车t＝5m/s×30s＝150m，‎ 由图知，n＝3，拉力端移动距离：‎ s＝3s车＝3×150m＝450m，‎ 拉力F在30s内所做的功：‎ W总＝Fs＝500N×450m＝2.25×105J；‎ ‎（2）地面对故障车的摩擦力：‎ f＝0.08G＝0.08mg＝0.08×1500kg×10N/kg＝1200N；‎ 滑轮组克服故障车摩擦力做的有用功：‎ W有用＝fs车＝1200N×150m＝1.8×105J，‎ 整个装置的机械效率：‎ η＝＝×100%＝80%。‎ ‎14．一定气压下，某种晶体熔化成同温度液体时所吸收的热量与其质量之比叫该晶体的熔化热，用字母λ表示。在标准大气压下，用一个热效率为40%的酒精炉为热源，将50g初温为0℃的冰全部熔化为0℃的水，共燃烧了14g酒精，酒精的热值为3×107J/kg。求：‎ ‎（1）冰熔化过程中吸收的热量；‎ 20‎ ‎（2）在标准大气压下，冰的熔化热λ冰。‎ ‎【答案】（1）冰熔化过程中吸收的热量为1.68×l05J；‎ ‎（2）在标准大气压下，冰的熔化热λ冰为3.36×106J/kg。‎ ‎【解析】（1）14g酒精完全燃烧放出的热量：‎ Q放＝qm′＝3×107J/kg×0.014kg＝4.2×l05J，‎ 由η＝可得，冰熔化成水共吸收热量：‎ Q吸＝Q放×η＝4.2×l05J×40%＝1.68×l05J；‎ ‎（2）则冰的熔化热：‎ λ冰＝＝＝3.36×106J/kg。‎ ‎15．已知天然气的热值为3.8×107J/m3，水的比热容为4.2×103J/（kg•℃）。求：‎ ‎（1）完全燃烧1.4×10﹣2m3天然气放出多少热量？‎ ‎（2）若某天然气灶的效率为60%，则这些天然气可将质量为3.8kg，初温为25℃的水加热到多少℃？（当地的大气压强为1标准大气压）‎ ‎【答案】（1）天然气放出的热量为5.32×105J；‎ ‎（2）这些天然气可将初温为25℃的水加热到45℃。‎ ‎【解析】（1）完全燃烧1.4×10﹣2m3天然气放出的热量：‎ Q放＝Vq＝1.4×10﹣2m3×3.8×107J/m3＝5.32×105J；‎ ‎（2）由η＝可得，水吸收的热量：‎ Q吸＝ηQ放＝60%×5.32×105J＝3.192×105J；‎ 由Q吸＝cm△t可得，水升高的温度：‎ ‎△t＝＝＝20℃，‎ 则水的末温度为：t＝t0+△t＝25℃+20℃＝45℃。‎ ‎16．如图所示，电源电压保持不变，电流表的量程为0～0.6A，电压表的量程为0～15V，R1＝20Ω，滑动变阻器R2的规格为“100Ω 1A”。‎ ‎（1）闭合开关S1，断开开关S2、S3，电流表示数为0.4A，求电源电压；‎ ‎（2）闭合开关S3，断开开关S1、S2，滑动变阻器滑片置于中点位置时，电压表的示数为 20‎ ‎4V，求R3的阻值；‎ ‎（3）闭合开关S1、S2和S3，在不损坏电流表、电压表的情况下，求滑动变阻器R2的阻值取值范围。‎ ‎【答案】（1）闭合开关S1，断开开关S2、S3，电流表示数为0.4A，电源电压为8V；‎ ‎（2）闭合开关S3，断开开关S1、S2，滑动变阻器滑片置于中点位置时，电压表的示数为4V，R3的阻值为50Ω；‎ ‎（3）闭合开关S1、S2和S3，在不损坏电流表、电压表的情况下，滑动变阻器R2的阻值取值范围为40Ω～100Ω。‎ ‎【解析】（1）闭合开关S1，断开开关S2、S3，为R1的简单电路，电流表示数为0.4A，‎ 根据欧姆定律可得，电源电压：‎ U＝I1R1＝0.4A×20Ω＝8V；‎ ‎（2）闭合开关S3，断开开关S1、S2，R2、R3串联，滑动变阻器滑片置于中点位置时，电压表（测变阻器的电压）的示数为4V，则电路中的电流：‎ I2＝＝＝0.08A，‎ 根据串联电路的规律和欧姆定律可得，R3的阻值：‎ R3＝＝＝50Ω；‎ ‎（3）闭合开关S1、S2和S3，R1、R2并联，电压表测电源电压，电流表测干路电流，‎ 根据并联电路各支路互不影响，通过R1的电流为0.4A不变，‎ 电流表的量程为0～0.6A，则干路电流最大为0.6A，‎ 由并联电路电流的规律，通过变阻器的最大电流：‎ I变大＝I总大﹣I1＝0.6A﹣0.4A＝0.2A，‎ 由欧姆定律可得，变阻器连入电路的最小电阻：‎ 20‎ R滑小＝＝＝40Ω；‎ 当变阻器滑片移动最左端时，变阻器接入阻值最大，总电流最小，没有超过电流表量程，故变阻器的最大电阻为100Ω，‎ 在不损坏电流表、电压表的情况下，滑动变阻器R2的阻值取值范围为40Ω～100Ω。‎ ‎17．空气质量指数是环境监测的重要指标，下表的空气质量等级是按照空气质量指数A划分的。某兴趣小组自制的空气质量监测仪，用电压表显示空气质量指数，工作原理电路图如图。已知电源电压U＝18V，电压表量程为0～15V，定值电阻R0的阻值为100Ω，气敏电阻阻值R与A的关系为R＝×103Ω 空气质量指数A ‎0〜50‎ ‎51〜100‎ ‎101〜150‎ ‎151〜200‎ ‎201〜300‎ ‎＞300‎ 空气质量等级 优 良 轻度污染 中度污染 重度污染 严重污染 ‎（1）通过计算，判断电压表示数为10V时对应的空气质量等级。‎ ‎（2）更换定值电阻R0可改变监测仪的测量范围，若要使电压表满偏时对应的空气质量指数A＝400，则更换后的定值电阻R′0的阻值应为多大？‎ ‎【答案】（1）电压表示数为10V时对应的空气质量等级为良；‎ ‎（2）更换后的定值电阻的阻值应为75Ω。‎ ‎【解析】由电路图可知，R0与R串联，电压表测R0两端的电压。‎ ‎（1）因串联电路中各处的电流相等，‎ 所以，当电压表示数为10V时，电路中的电流：‎ I＝＝＝0.1A，‎ 因串联电路中总电压等于各分电压之和，‎ 所以，气敏电阻R两端的电压：‎ UR＝U﹣U0＝18V﹣10V＝8V，‎ 则此时气敏电阻的阻值：‎ 20‎ R＝＝＝80Ω，‎ 此时的空气质量指数：A＝×103Ω＝75，‎ 由51＜75＜100可知，此时空气质量等级为良；‎ ‎（2）空气质量指数A＝400时，气敏电阻的阻值：‎ R′＝×103Ω＝15Ω，‎ 由题意可知，此时电压表的示数U0′＝15V，则气敏电阻两端的电压：‎ UR′＝U﹣U0′＝18V﹣15V＝3V，‎ 此时电路中的电流：‎ I′＝＝＝0.2A，‎ 则更换后的定值电阻的阻值：‎ R0′＝＝＝75Ω。‎ ‎18．甜甜要制作一个电动航模，需要电动机作为动力源，她找来电吹风，研究了电吹风的工作原理。如图甲，电吹风工作时，可以分别吹出热风和冷风，为了防止温度过高，用一个PTC电阻R0与电阻为50Ω的电热丝R串联，R0的阻值随温度的变化如图乙所示，请回答下列问题：‎ ‎（1）PTC电阻是由　半导体　材料制成的；电动机的工作原理是　通电导体在磁场中受到力的作用　。‎ ‎（2）电吹风吹热风时，求电热丝的最大发热功率。‎ ‎（3）电吹风吹冷风时，通过电动机的电流为1A，工作20s，电动机的机械效率为90%，求电动机线圈电阻。（不计机械摩擦损耗的能量）‎ ‎【答案】（1）半导体；通电导体在磁场中受到力的作用；‎ 20‎ ‎（2）电吹风吹热风时，电热丝的最大发热功率为672.2W；‎ ‎（3）电动机线圈电阻为22Ω。‎ ‎【解析】（1）由图乙可知，PTC电阻R0的阻值随温度的变化而变化，是由半导体材料制成的；‎ 电动机的工作原理是：通电导体在磁场中受到力的作用；‎ ‎（2）由图乙可知，R0的最小阻值为10Ω，此时电热丝支路的总电阻最小，该支路中的电流最大，电热丝的发热功率最大，‎ 因串联电路中总电阻等于各分电阻之和，‎ 所以，电热丝支路中的电流：‎ I大＝＝＝A，‎ 则电热丝的最大发热功率：‎ P热＝I大2R＝（A）2×50Ω≈672.2W ‎（3）电吹风吹冷风时，通过电动机的电流为1A，工作20s，消耗的电能：‎ W电＝UIt＝220V×1A×20s＝4400J，‎ 由η＝×100%可得，输出的机械能：‎ W机械＝W电η＝4400J×90%＝3960J，‎ 电动机线圈电阻产生的热量：‎ Q＝W电﹣W机械＝4400J﹣3960J＝440J，‎ 由Q＝I2Rt可得，电动机线圈的电阻：‎ R线圈＝＝＝22Ω。‎ ‎19．如图所示电路，电源电压为5V不变，定值电阻R0阻值为5Ω，滑动变阻器R上标有“20Ω 1A”字样，灯L标有“3V 1.2W”，电压表量程为0～3V．（不考虑灯丝电阻的变化，且保证各元件均安全）求：‎ ‎（1）当S1闭合、S2接b，灯泡正常发光时，滑动变阻器接入电路的阻值是多少？‎ ‎（2）保持滑动变阻器滑片位置不动，当S1闭合、S2接a时，R0的电功率是多少？‎ ‎（3）当S1闭合、S2接a时，R0的最小电功率是多少？‎ 20‎ ‎【答案】（1）当S1闭合、S2接b，灯泡正常发光时，滑动变阻器接入电路的阻值是5Ω；‎ ‎（2）保持滑动变阻器滑片位置不动，当S1闭合、S2接a时，R0的电功率是1.25W；‎ ‎（3）当S1闭合、S2接a时，R0的最小电功率是0.8W。‎ ‎【解析】（1）当S1闭合、S2接b时，灯泡L与变阻器R串联，电压表测R两端的电压，‎ 因串联电路中各处的电流相等，且灯泡正常发光，‎ 所以，由P＝UI可得，电路中的电流：‎ I＝＝＝0.4A，‎ 因串联电路中总电压等于各分电压之和，‎ 所以，滑动变阻器两端的电压：‎ UR＝U﹣UL＝5V﹣3V＝2V，‎ 由I＝可得，滑动变阻器接入电路的阻值：‎ R＝＝＝5Ω；‎ ‎（2）保持滑动变阻器滑片位置不动，当S1闭合、S2接a时，定值电阻R0与变阻器R串联，‎ 因串联电路中总电阻等于各分电压之和，‎ 所以，电路中的电流：‎ I′＝＝＝0.5A，‎ 则R0的电功率：‎ P0＝（I′）2R0＝（0.5A）2×5Ω＝1.25W；‎ ‎（3）当S1闭合、S2接a时，定值电阻R0与变阻器R串联，电压表测R两端的电压，电流表测电路中的电流，‎ 当电压表的示数UR′＝3V时，R0两端的电压：‎ 20‎ U0＝U﹣UR′＝5V﹣3V＝2V，‎ 此时电路中的电流：‎ I″＝＝＝0.4A，‎ 此时变阻器接入电路中的电阻：‎ R′＝＝＝7.5Ω，‎ 所以，电路中的最小电流为0.4A，此时R0的电功率最小，则 P0小＝（I″）2R0＝（0.4A）2×5Ω＝0.8W。‎ ‎20．如图所示，某品牌智能电火锅的铭牌，（不计温度对电阻的影响）。求：‎ ‎（1）该电火锅锅正常加热30分钟时所消耗的电能为多少kW•h？‎ ‎（2）某天用电高峰期，只使用电火锅加热10min，家用电能表（1200r/kW．h）的转盘转了200转，此时电火锅的实际功率是多少？‎ ‎（3）如图乙所示是电火锅的简化电路图，其中R1、R2均为发热电阻，S2为加热保温自动切换开关，求R2的电阻是多少？‎ XX牌智能电火锅 型号 ZDF﹣215‎ 额定电压 ‎220V 加热功率 ‎1210W 保温功率 ‎484W 频率 ‎50Hz ‎【答案】（1）该电火锅锅正常加热30分钟时所消耗的电能为0.605kW•h；（2）此时电火锅的实际功率是1000W；（3）R2的电阻是60Ω。‎ ‎【解析】（1）由P＝可得，电火锅正常工作时间为30min消耗的电能：‎ W总＝Pt总＝1.21kW×0.5h＝0.605kW•h；‎ 20‎ ‎（2）转200转消耗的电能：‎ W＝×200r＝kW•h，‎ 此时消耗的实际功率：‎ P实＝＝＝1kW＝1000W；‎ ‎（3）由图知，当S1闭合、S2接a时，电路中只有R1，电路中电阻最小，由P＝可知此时电功率最大，处于加热状态；‎ 由P＝得电火锅正常加热时的电阻：‎ R1＝＝＝40Ω；‎ 由图知，当S1闭合、S2接b时，电路中R1和R2串联，电路中电阻最大，由P＝可知此时电功率最小，处于保温状态；‎ 由P＝得串联总电阻：‎ R串＝R1+R2＝＝＝100Ω，‎ R2的电阻：‎ R2＝R串﹣R1＝100Ω﹣40Ω＝60Ω；‎ 20‎