2008年北京市宣武区中考数学二模试卷 13页

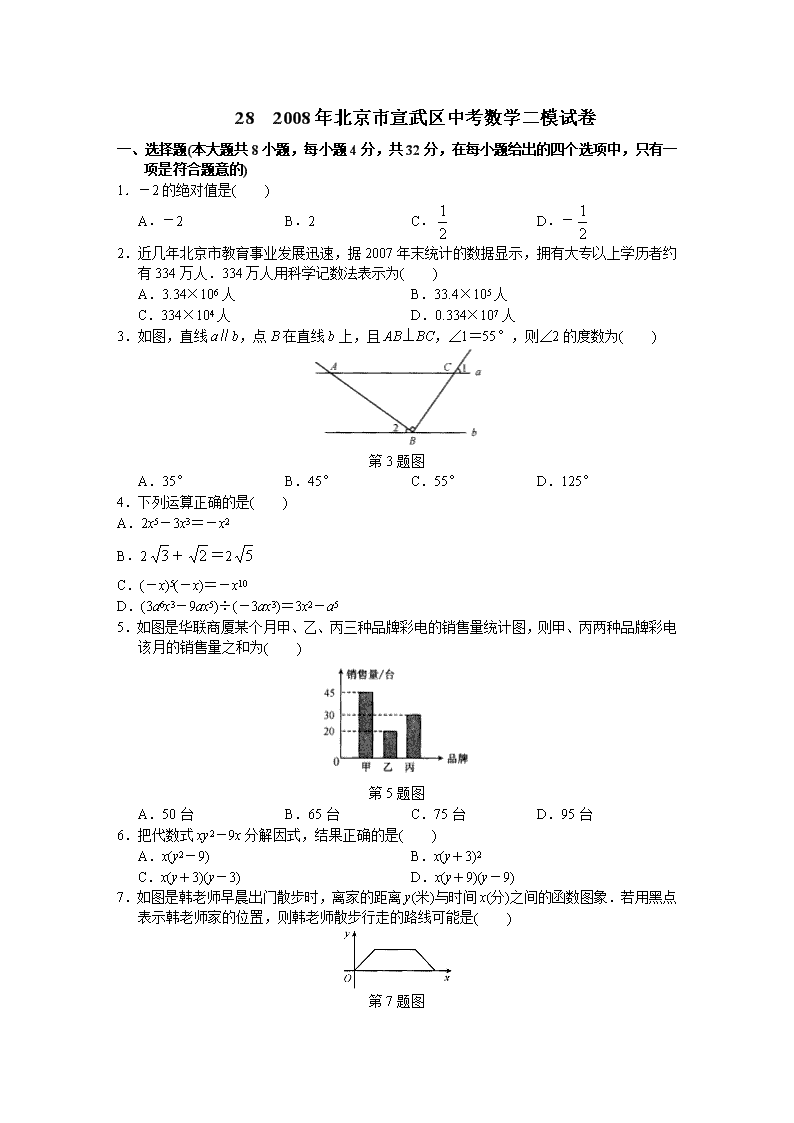
‎28 2008年北京市宣武区中考数学二模试卷 一、选择题(本大题共8小题，每小题4分，共32分，在每小题给出的四个选项中，只有一项是符合题意的)‎ ‎1．－2的绝对值是( )‎ A．－2 B．‎2 ‎C． D．－‎ ‎2．近几年北京市教育事业发展迅速，据2007年末统计的数据显示，拥有大专以上学历者约有334万人．334万人用科学记数法表示为( )‎ A．3.34×106人 B．33.4×105人 C．334×104人 D．0.334×107人 ‎3．如图，直线a∥b，点B在直线b上，且AB⊥BC，∠1＝55°，则∠2的度数为( )‎ 第3题图 A．35° B．45° C．55° D．125°‎ ‎4．下列运算正确的是( )‎ A．2x5－3x3＝－x2‎ B．2＋＝2‎ C．(－x)5(－x)＝－x10‎ D．(‎3a6x3－9ax5)÷(－3ax3)＝3x2－a5‎ ‎5．如图是华联商厦某个月甲、乙、丙三种品牌彩电的销售量统计图，则甲、丙两种品牌彩电该月的销售量之和为( )‎ 第5题图 A．50台 B．65台 C．75台 D．95台 ‎6．把代数式xy2－9x分解因式，结果正确的是( )‎ A．x(y2－9) B．x(y＋3)2‎ C．x(y＋3)(y－3) D．x(y＋9)(y－9)‎ ‎7．如图是韩老师早晨出门散步时，离家的距离y(米)与时间x(分)之间的函数图象．若用黑点表示韩老师家的位置，则韩老师散步行走的路线可能是( )‎ 第7题图 ‎8．将边长为‎8cm的正方形ABCD的四边沿直线l向右滚动(不滑动)，当正方形滚动两周时，正方形的顶点A所经过的路线的长是( )‎ 第8题图 A．(4p ＋8p )cm B．(8p ＋16p )cm C．(8p ＋8p )cm D．(4＋16p )cm 二、填空题(本大题共4小题，每小题4分，共16分，把答案写在题中横线上)‎ ‎9．函数的自变量x的取值范围是________．‎ ‎10．数据12，10，13，8，17，10，21的中位数是________．‎ ‎11．如图，在菱形ABCD中，∠B＝60°，点E、F分别从点B、D出发以同样的速度沿边BC、DC向点C运动．给出以下四个结论：①AE＝AF；②∠CEF＝∠CFE；③当点E、F分别为边BC、DC的中点时，△AEF是等边三角形；④当点E、F分别为边BC、DC的中点时，△AEF的面积最大．上述结论中正确的有________．(把你认为正确的结论的序号都填上)‎ ‎ ‎ 第11题图 第12题图 ‎12．如图，已知A1(1，0)，A2(1，1)，A3(－1，1)，A4(－1，－1)，A5(2，－1)，则点A2008的坐标为________．‎ 三、解答题(共13个小题，共72分)‎ ‎13．(5分)已知a＝sin60°，b＝cos45°，c＝，d＝－1，从a、b、c、d这4个数中任意选取3个数求和．‎ ‎14．(5分)用配方法解方程：2x2－x－1＝0．‎ ‎15．(5分)化简：．‎ ‎16．(5分)已知a＝，b＝2，求代数式(a＋b)2－‎2a(b＋1)－a2b÷b的值．‎ ‎17．(5分)已知：如图，在△ABC中，D为AB边上一点，AC＝BC，AC2＝AB·AD．求证：△ADC是等腰三角形．‎ 第17题图 ‎18．(5分)如图，已知：AD＝AE，AB＝AC．‎ ‎(1)求证：∠B＝∠C；‎ ‎(2)若∠A＝50°，问△ADC经过怎样的变换能与△AEB重合．‎ 第18题图 ‎19．(5分)如图，已知点O为Rt△ABC斜边AB上一点，以O为圆心，OA为半径的圆与BC相切于点D，与AB相交于点E，与AC相交于点F．试判断AD是否平分∠BAC．并说明理由．‎ 第19题图 ‎20．(6分)“石头、剪刀、布”是广为流传的游戏．游戏时甲、乙双方每次出“石头”“剪刀”“布”三种手势中的一种，规定“石头”胜“剪刀”、“剪刀”胜“布”、“布”胜“石头”，同种手势不分胜负．假定甲、乙两人每次都是等可能地出这三种手势，用画树状图或列表的方法分别求出一次游戏中两人出同种手势的概率和甲获胜的概率．(提示：为书写方便，解答时可以用S表示“石头”，用J表示“剪刀”，用B表示“布”)‎ ‎21．(5分)2008年北京奥运会的比赛部分门票已接受公众预订．下表为北京奥运会官方票务网站公布的几种球类比赛的门票价格，某同学一家准备用8 000元预订10张下表中比赛项目的门票．‎ ‎(1)若全部资金用来预订男篮门票和乒乓球门票，问可以订男篮门票和乒乓球门票各多少张．‎ ‎(2)若在现有资金8 000元允许的范围内和总票数不变的前提下，想预订下表中三种球类门票，其中男篮门票数与足球门票数相同，且乒乓球门票的费用不超过男篮门票的费用，求这个家庭能预订三种球类门票各多少张.‎ 比赛项目 票价(元／场)‎ 男篮 ‎1000‎ 足球 ‎800‎ 乒乓球 ‎500‎ ‎22．(4分)如图，已知直线l1经过点A(－1，0)与点B(2，3)，另一条直线l2经过点B，且与x轴相交于点P(m，0)．‎ ‎(1)求直线l1的解析式；‎ ‎(2)若△APB的面积为3，求m的值．‎ 第22题图 ‎23．(7分)在四边形ABCD中，对角线AC平分∠DAB．‎ ‎(1)如图①，当∠DAB＝120°，∠B＝∠D＝90°时，求证：AB＋AD＝AC．‎ ‎(2)如图②，当∠DAB＝120°，∠B与∠D互补时，线段AB、AD、AC有怎样的数量关系?写出你的猜想，并给予证明．‎ ‎(3)如图③，当∠DAB＝90°，∠B与∠D互补时，线段AB、AD、AC有怎样的数量关系?写出你的猜想，并给予证明．‎ 第23题图 ‎24．(7分)已知二次函数图象的对称轴为直线x＝2，图象经过两点(0，3)和(－1，8)，并与x轴的交点为B、C(点C在点B左边)，其顶点为点P．‎ ‎(1)求此二次函数的解析式．‎ ‎(2)如果直线y＝x向上或向下平移经过点P，求证：平移后的直线一定经过点B．‎ ‎(3)在(2)的条件下，能否在直线y＝x上找一点D，使四边形OPBD是等腰梯形?若能，请求出点D的坐标；若不能，请简要说明你的理由．‎ ‎25．(8分)已知正方形ABCD和等腰Rt△BEF，BE＝EF，∠BEF＝90°，按图①放置，使点F在BC上，取DF的中点G，连结EG、CG．‎ ‎(1)探索EG、CG的数量关系和位置关系并证明；‎ ‎(2)将图①中△BEF绕B点顺时针旋转45°，再连结DF，取DF中点G(如图②)，问(1)中的结论是否仍然成立．证明你的结论；‎ ‎(3)将图①中△BEF绕B点转动任意角度(旋转角在0°到90°之间)，再连结DF，取DF的中点G(如图③)，问(1)中的结论是否仍然成立，证明你的结论．‎ 第25题图 答 案 ‎28．2008年北京市宣武区中考数学二模试卷 一、选择题 ‎1．B 2．A 3．A 4．D 5．C 6．C 7．D 8．B 二、填空题 ‎9．x≠5 10．12 11．①②③ 12．(－502，－502)‎ 三、解答题 ‎13．解：由已知得，，，．‎ ‎．‎ 其他情况如下：‎ ‎．‎ ‎．‎ ‎．‎ ‎14．解：两边都除以2，得移项，得．‎ 配方，得，．‎ 或．，．‎ ‎15．解法一：原式．‎ 解法二：原式 ‎．‎ 解法三：原式．‎ ‎16．解：原式＝a2＋2ab＋b2－2ab－‎2a－a2＝b2－‎2a．‎ 当，b＝2时，原式．‎ ‎17．证明：在△ABC中，AC＝BC，∠B＝∠A．∵AC2＝AB·AD，‎ 又∵∠A＝∠A，∴△ABC∽△ACD．∴∠B＝∠ACD，‎ ‎∴∠ACD＝∠A，∴△ADC是等腰三角形．‎ ‎18．(1)证明：在△AEB与△ADC中，AB＝AC，∠A＝∠A，AE＝AD，‎ ‎∴△AEB≌△ADC．∴∠B＝∠C．‎ ‎(2)解：先将△ADC绕点A逆时针旋转50°，再将旋转后的三角形沿直线AE对折，即可得△ADC与△AEB重合．或先将△ADC绕点A顺时针旋转50°，再将旋转后的三角形沿直线AB对折，即可得△ADC与△AEB重合．(答案不唯一)‎ ‎19．解：AD平分∠BAC．‎ 证明如下：连结OD．∵BC切⊙O于D，‎ ‎∴OD⊥BC．‎ ‎∵△ABC为直角三角形，且∠C＝90°，‎ ‎∴AC⊥BC．∴OD∥AC，∴∠1＝∠2，‎ 又∵OA＝OD，∴∠3＝∠2，‎ ‎∴∠1＝∠3．故AD平分∠BAC．‎ 第19题答图 ‎20．解法一：一次游戏，甲、乙两人随机出手势的所有可能的结果如图所示：‎ 第20题答图 所有可能出现的结果为(S，S)、(S，J)、(S，B)、‎ ‎(J，S)、(J，J)、(J，B)、(B，S)、(B，J)、(B，B)．从上面树状图可以看出，一次游戏可能出现的结果共有9种，而且每种结果出现的可能性相同．所以，P(出同种手势)＝；P(甲获胜)＝．‎ 解法二：一次游戏，甲、乙两人随机出手势的所有可能的结果如下表所示：‎ ‎ 乙出的手势 甲出的手势 S J B S ‎(S，S)‎ ‎(S，J)‎ ‎(S，B)‎ J ‎(J，S)‎ ‎(J，J)‎ ‎(J，B)‎ B ‎(B，S)‎ ‎(B，J)‎ ‎(B，B)‎ 以下同解法一．‎ ‎21．(1)解：设预订男篮门票x张，则预订乒乓球门票(10－x)张．‎ 由题意，得1000x＋500(10－x)＝8000．解得x＝6．∴10－x＝4．‎ 答：可预订男篮门票6张，乒乓球门票4张．‎ ‎(2)解法一：设男篮门票与足球门票都预订a张，则预订乒乓球门票(10－‎2a)张．‎ ‎1000a‎＋‎800a＋500(10－‎2a)≤8000，‎ 由题意，得500(10－‎2a)≤‎1000a．‎ 解得．由a为正整数可得a＝3．∴10－‎2a＝4．‎ 答：这个家庭能预订男篮门票3张，足球门票3张，乒乓球门票4张．‎ 解法二：设男篮门票与足球门票都预订a张，则预订乒乓球门票(10－‎2a)张．‎ ‎500(10－‎2a)≤‎1000a，由题意，得 解得．由a为正整数可得a＝3或a＝4．‎ 当a＝3时，总费用为3×1000＋3×800＋4×500＝7400(元)＜8000(元)，‎ 当a＝4时，总费用为4×1000＋4×800＋2×500＝8200(元)＞8000(元)，不合题意，舍去．‎ 答：这个家庭能预订男篮门票3张，足球门票3张，乒乓球门票4张．‎ ‎22．解：(1)设直线l1的解析式为y＝kx＋b，由题意，得 解得所以，直线l1的解析式为y＝x＋1．‎ ‎(2)当点P在点A的右侧时，AP＝m－(－1)＝m＋1，有×3＝3，解得m＝1，此时点P的坐标为(1，0)；‎ 当点P在点A的左侧时，AP＝－1－m，有，解得m＝－3，此时，点P的坐标为(－3，0)．‎ 综上所述，m的值为1或－3．‎ ‎23．解：(1)在四边形ABCD中，∵AC平分∠DAB，∠DAB＝120°，‎ ‎∴∠CAB＝∠CAD＝60°．又∵∠B＝∠D＝90°，‎ ‎∴∠ACB＝∠ACD＝30°．，即AB＋AD＝AC．‎ ‎(2)AB＋AD＝AC．‎ 证明如下：如图①，过C点分别作AD和AB延长线的垂线段，垂足分别为E、F．‎ ‎∵AC平分∠DAB，‎ ‎∴CE＝CF．‎ ‎∵∠ABC＋∠D＝180°，‎ ‎∠ABC＋∠CBF＝180°，‎ ‎∴∠CBF＝∠D．‎ 又∵∠CED＝∠CFB＝90°，‎ ‎∴△CED≌△CFB．∴ED＝BF．‎ ‎∴AD＋AB＝AE＋ED＋AB＝AE＋BF＋AB＝AE＋AF．‎ 由(1)知AE＋AF＝AC．‎ ‎∴AB＋AD＝AC．‎ 第23题答图①‎ 第23题答图②‎ ‎(3)AB＋AD＝AC．‎ 证明如下：如图②，过C点分别作AB和AD延长线的垂线段，垂足分别是E、F．‎ ‎∵AC平分∠DAB，∴CE＝CF．‎ ‎∵∠ABC＋∠ADC＝180°，‎ ‎∠ADC＋∠FDC＝180°，‎ ‎∴∠ABC＝∠FDC．‎ 又∵∠CEB＝∠CFD＝90°．‎ ‎∴△CEB≌△CFD．∴CB＝CD．‎ 延长AB至G，使BG＝AD，连结CG．‎ ‎∵∠ABC＋∠ADC＝180°，∠ABC＋∠CBG＝180°，‎ ‎∴∠CBG＝∠ADC．∴△GBC≌△ADC．‎ ‎∴∠G＝∠DAC＝∠CAB＝45°．∴∠ACG＝90°．‎ ‎．‎ ‎．‎ ‎24．解：(1)设二次函数的解析式为y＝a(x－2)2＋m，‎ ‎∵抛物线经过点(0，3)和(－1，8)，‎ 解得 ‎∴二次函数的解析式为y＝(x－2)2－1＝x2－4x＋3．‎ ‎(2)抛物线y＝x2－4x＋3与戈轴的交点为B(3，0)、C(1，0)，顶点为P(2，－1)．‎ 由题意，设平移后直线为y＝x＋b．‎ 由已知得，－1＝2＋b，解得b＝－3．‎ ‎∴直线y＝x平移后经过点P的直线为y＝x－3．‎ 当x＝3时，y＝0．‎ ‎∴直线y＝x－3经过点B(3，0)．‎ ‎(3)能，点D的坐标为(2，2)，理由如下：如图，过点D作DM⊥x轴于点肘，过点P作PN⊥x轴于点N．‎ 在Rt△ONP中，OP2＝ON 2＋PN2＝5．‎ ‎∵点D在直线y＝x上，∴设点D的坐标为(x，x)．‎ 在Rt△BDM中，‎ BD2＝BM2＋DM2＝(3－x)2＋x2．‎ 由OP2＝BD2得(3－x)2＋x2＝5．‎ 解得x1＝2，x2＝1．当x＝1时，四边形OPBD为平行四边形，舍去．‎ ‎∴x＝2．∴点D的坐标为(2，2)．‎ 第24题答图 ‎25．解：(1)EG＝CG且EG⊥CG．‎ 证明如下：如图①，连结BD．‎ ‎∵正方形ABCD和等腰Rt△BEF，‎ ‎∴∠EBF＝∠DBC＝45°．∴B、E、D三点共线．‎ ‎∵∠DEF＝90°，G为DF的中点，∠DCB＝90°，‎ ‎∴EG＝DG＝GF＝CG．‎ ‎∴∠EGF＝2∠EDG，∠CGF＝2∠CDG．‎ ‎∴∠EGF＋∠CGF＝2∠EDC＝90°，‎ 即∠EGC＝90°，∴EG⊥CG．‎ ‎(2)仍然成立，‎ 证明如下：如图②，延长EC交CD于点H．‎ ‎∵BE⊥EF，∴EF∥CD，∴∠1＝∠2．‎ 又∵∠3＝∠4，FG＝DG，‎ ‎∴△FEG≌△DHG，‎ ‎∴EF＝DH，EG＝GH．‎ ‎∵△BEF为等腰直角三角形，‎ ‎∴BE＝EF，∴BE＝DH．‎ ‎∵CD＝BC,∴CE＝CH．‎ ‎∴△ECH为等腰直角三角形．‎ 又∵EG＝GH，‎ ‎∴EG＝CG且EG⊥CG．‎ ‎(3)仍然成立．‎ 证明如下：如图③，延长CG至H，使GH＝CG，连结HF交BC于M，连结EH、EC．‎ ‎∵GF＝GD，∠HGF＝∠CGD，HG＝CG，‎ ‎∴△HFG≌△CDG，‎ ‎∴HF＝CD，∠GHF＝∠GCD，‎ ‎∴HF//CD．∵正方形ABCD，‎ ‎∴HF＝BC，HF⊥BC．‎ ‎∵△BEF是等腰直角三角形，‎ ‎∴BE＝EF，∠EBC＝∠HFE，‎ ‎∴△BEC≌△FEH，∴HE＝EC，∠BEC＝∠FEH，‎ ‎∴∠BEF＝∠HEC＝90°，∴△ECH为等腰直角三角形．又∵CG＝GH，∴EG＝CG且EG⊥CG．‎ 第25题答图①‎ 第25题答图②‎ 第25题答图③‎