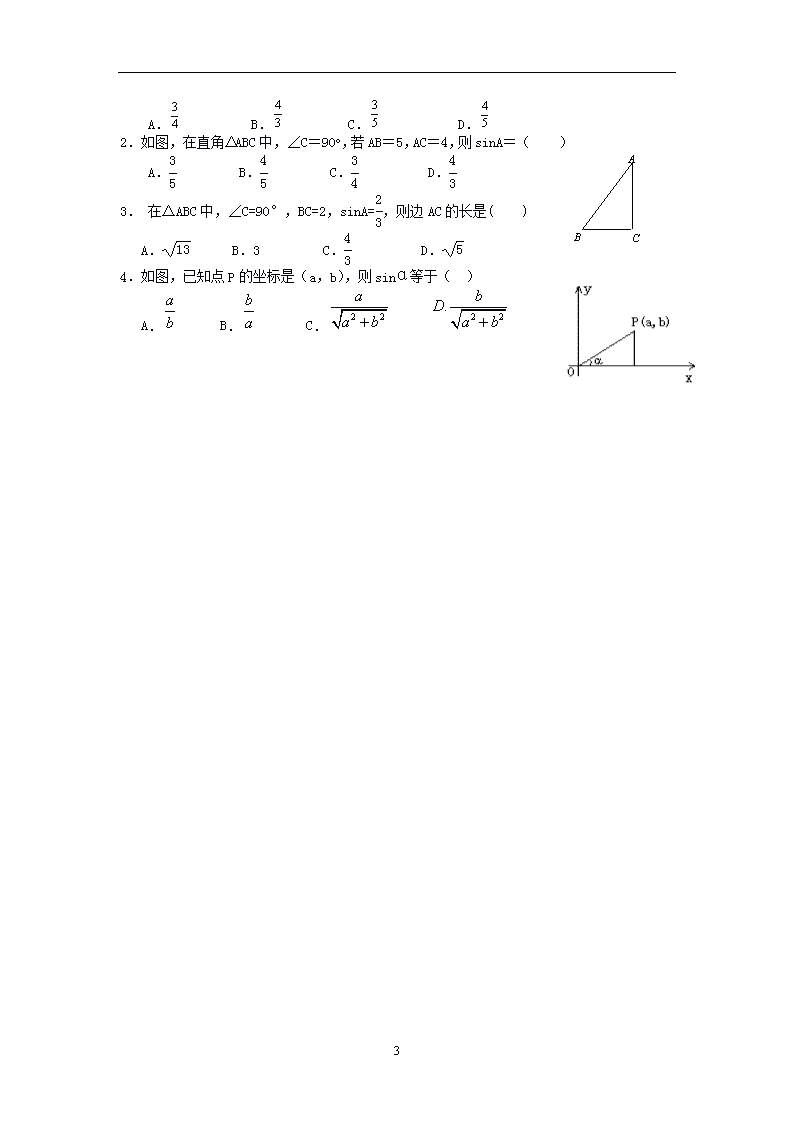锐角三角函数：正弦4 3页

‎ ‎ ‎ 锐角三角函数 第一课时 ‎28．1．1锐角三角函数（1） ——正弦 ‎【学习目标】‎ ‎⑴: 经历当直角三角形的锐角固定时，它的对边与斜边的比值都固定（即正弦值不变）这一事实。 ‎ ‎⑵: 能根据正弦概念正确进行计算 ‎【学习重点】‎ 理解正弦（sinA）概念，知道当直角三角形的锐角固定时，它的对边与斜边的比值是固定值这一事实．‎ ‎【学习难点】‎ 当直角三角形的锐角固定时，，它的对边与斜边的比值是固定值的事实。‎ ‎【导学过程】‎ 一、自学提纲：‎ ‎1、如图在Rt△ABC中，∠C=90°，∠A=30°，BC=10m，求AB ‎2、如图在Rt△ABC中，∠C=90°，∠A=30°，AB=20m，求BC 二、合作交流：‎ 问题： 为了绿化荒山，某地打算从位于山脚下的机井房沿着山坡铺设水管，在山坡上修建一座扬水站，对坡面的绿地进行喷灌．现测得斜坡与水平面所成角的度数是30°，为使出水口的高度为35m，那么需要准备多长的水管？‎ 思考1：如果使出水口的高度为50m，那么需要准备多长的水管？ ； 如果使出水口的高度为a m，那么需要准备多长的水管？ ；‎ 结论：直角三角形中，30°角的对边与斜边的比值 ‎ 思考2：在Rt△ABC中，∠C=90°，∠A=45°，∠A对边与斜边的比值是一个定值吗？如果是，是多少？‎ 结论：直角三角形中，45°角的对边与斜边的比值 ‎ ‎ ‎ 三、教师点拨：‎ 从上面这两个问题的结论中可知，在一个Rt△ABC中，∠C=90°，当∠A=30°时，∠A的对边与斜边的比都等于，是一个固定值；当∠A=45°时，∠A 3‎ ‎ ‎ 的对边与斜边的比都等于，也是一个固定值．这就引发我们产生这样一个疑问：当∠A取其他一定度数的锐角时，它的对边与斜边的比是否也是一个固定值？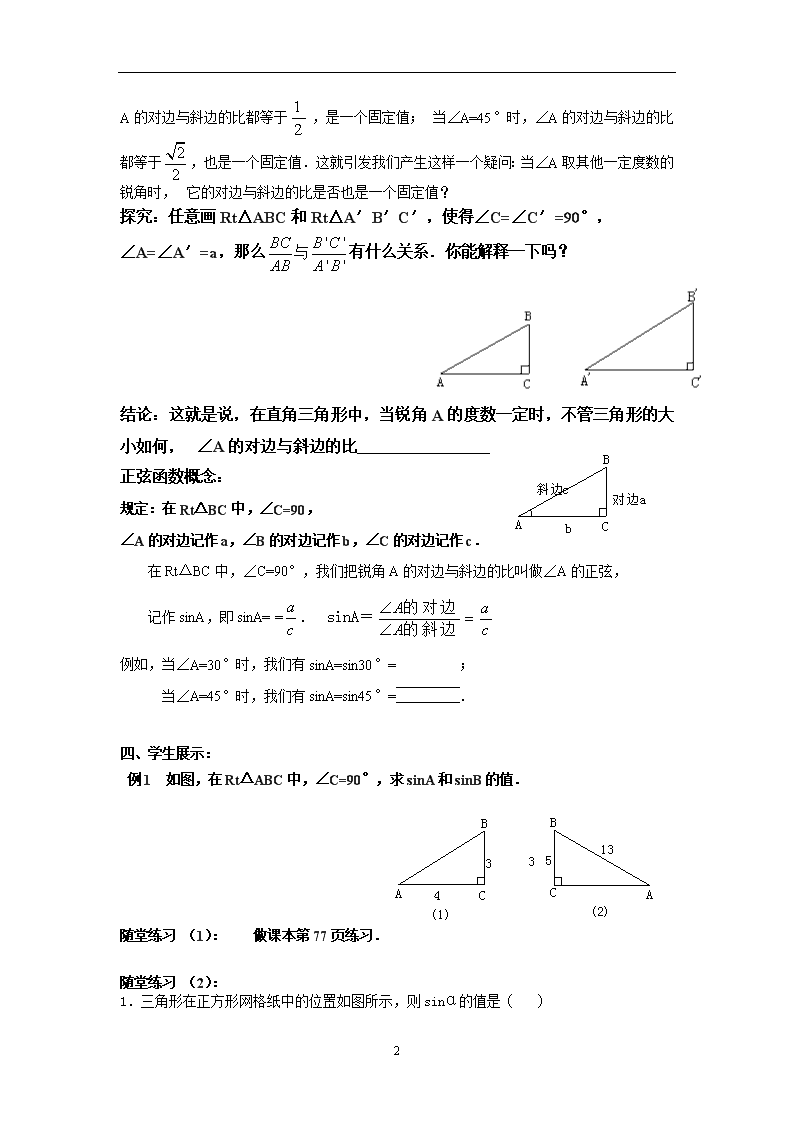‎ 探究：任意画Rt△ABC和Rt△A′B′C′，使得∠C=∠C′=90°，‎ ‎∠A=∠A′=a，那么有什么关系．你能解释一下吗？‎ ‎ ‎ 结论：这就是说，在直角三角形中，当锐角A的度数一定时，不管三角形的大小如何，∠A的对边与斜边的比 ‎ 正弦函数概念：‎ 规定：在Rt△BC中，∠C=90，‎ ‎∠A的对边记作a，∠B的对边记作b，∠C的对边记作c．‎ 在Rt△BC中，∠C=90°，我们把锐角A的对边与斜边的比叫做∠A的正弦，‎ 记作sinA，即sinA= =． sinA＝‎ 例如，当∠A=30°时，我们有sinA=sin30°= ；‎ 当∠A=45°时，我们有sinA=sin45°= ．‎ 四、学生展示：‎ 例1 如图，在Rt△ABC中，∠C=90°，求sinA和sinB的值．‎ ‎ ‎ 随堂练习 （1）： 做课本第77页练习．‎ 随堂练习 （2）：‎ ‎1．三角形在正方形网格纸中的位置如图所示，则sinα的值是﹙ ﹚‎ ‎ A． B． C． D．‎ ‎2．如图，在直角△ABC中，∠C＝90o，若AB＝5，AC＝4，则sinA＝（ ）‎ 3‎ ‎ ‎ A． 　B． C． 　D． ‎3． 在△ABC中，∠C=90°，BC=2，sinA=，则边AC的长是( )‎ A． B．3 C． D． ‎ ‎4．如图，已知点P的坐标是（a，b），则sinα等于（ ）‎ A． B． C．‎ 3‎