2020九年级数学上册 第二十四章 圆 24 2页

第2课时 圆锥的侧面积和全面积 ‎※教学目标※‎ ‎【知识与技能】‎ ‎ 掌握圆锥的特征，弄清圆锥侧面展开图中各元素与圆锥中各元素之间的对应关系；会推导、计算圆锥的侧面积和全面积.‎ ‎【过程与方法】‎ ‎ 通过对圆锥侧面积的推导，体会空间图形平面化的数学方法；发展类比和转化的数学思想；进一步培养空间观念.‎ ‎【情感态度】‎ 通过对实际问题的分析，体会数学的实用价值；在小组活动中培养合作交流能力和探究精神.‎ ‎【教学重点】‎ ‎ 1.理解圆锥侧面积和全面积的公式及其有关计算.‎ ‎ 2.培养学生空间观念及空间图形与平面图形相互转化的思想.‎ ‎【教学难点】‎ ‎1.利用圆锥的侧面积和全面积的公式解决实际问题.‎ ‎2.圆锥侧面展开图（扇形）中各元素与圆锥各元素之间的关系.‎ ‎※教学过程※‎ 一、情境导入 ‎（课件出示生活中常见的圆锥的图片）圆锥可以看作是一个直角三角形绕它的一条直角边旋转一周所成的图形.你知道圆锥各部分的名称吗？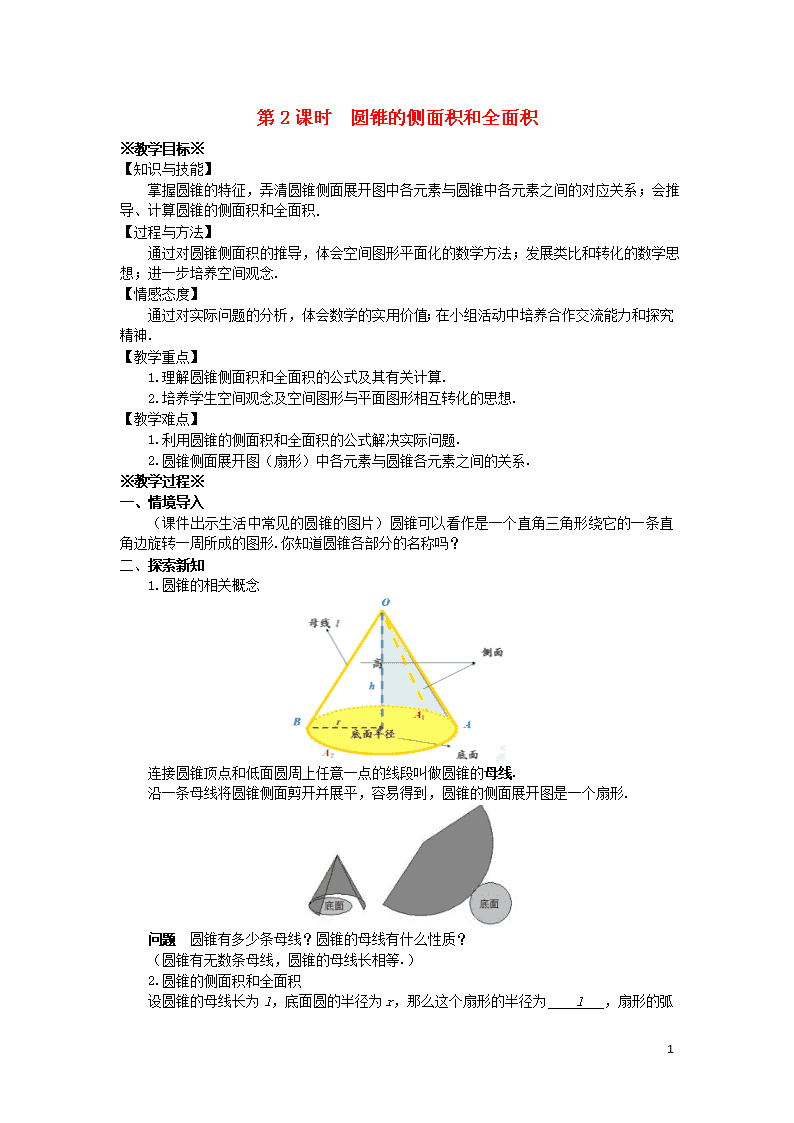‎ 二、探索新知 ‎1.圆锥的相关概念 ‎ 连接圆锥顶点和低面圆周上任意一点的线段叫做圆锥的母线.‎ 沿一条母线将圆锥侧面剪开并展平，容易得到，圆锥的侧面展开图是一个扇形.‎ 问题 圆锥有多少条母线？圆锥的母线有什么性质？‎ ‎（圆锥有无数条母线，圆锥的母线长相等.）‎ 2. 圆锥的侧面积和全面积 ‎ 设圆锥的母线长为l，底面圆的半径为r，那么这个扇形的半径为 l ‎ 2‎ ‎，扇形的弧长为 2πr ，因此圆锥的侧面积为 ，圆锥的全面积为 .‎ 三、 掌握新知 ‎ 例 蒙古包可以近似地看作由圆锥和圆柱组成.如果想用毛毡搭建20个底面积为‎12m2‎，高为‎3.2m，外围高‎1.8m的蒙古包，至少需要多少平方米的毛毡 (π取3.142，结果取整数) ？‎ 解：如图是一个蒙古包的示意图.‎ 根据题意，下部圆柱的底面积为‎12m2‎，高h2=‎1.8m；上部圆锥的高h1=3.2-1.8=1.4(m）.圆柱的底面半径r=≈1.954(m），侧面积为2π×1.954×1.8≈22.10(m2）.圆锥的母线长l=≈2.404(m），侧面展开扇形的弧长为2π×1.954≈12.28(m2），圆锥的侧面积为×2.404×12.28≈14.76(m2）.因此，搭建20个这样的蒙古包至少需要毛毡20×(22.10+14.76)≈738(m2）.‎ 四、巩固练习 ‎ 1.已知圆锥的高是‎30cm,母线长是‎50cm，则圆锥的侧面积是 .‎ ‎2.已知圆锥的底面半径为‎4cm，高为‎3cm，则这个圆锥的侧面积为 cm2.‎ ‎3.圆锥的底面直径为‎80cm.母线长为‎90cm，它的全面积为 .‎ ‎ 4.扇形的半径为30,圆心角为120°用它做一个圆锥模型的侧面,这个圆锥的底面半径为 ，高为 .‎ ‎ 答案：1.2000πcm2 2.20π 3.520πcm2 4.10，20 ‎ 五、归纳小结 ‎ 本节课你学到了什么知识？你有什么认识？‎ ‎※布置作业※‎ ‎ 从教材习题21.3中选取．‎ ‎※教学反思※‎ ‎1.在本节课从观察圆锥模型开始，通过猜想侧面展开图的形状，然后由老师具体操作验证结论的正确性，并能运用所学知识推导出圆锥的侧面积和全面积公式，培养了学生观察、猜想、探索等方面的能力.‎ ‎2.本小节教材是复习圆周长公式推出弧长公式，复习圆面积公式推出扇形面积公式，是在小学基础知识上的提升，圆柱和圆锥的侧面积计算，是将立体图形转化为平面图形，通过具体操作，学生可以获得直观的感受，对于学习高中立体几何有很大的帮助.‎ ‎ ‎ 2‎