鄂尔多斯专版2020中考数学复习方案第二单元方程组与不等式组第06课时一元二次方程及其应用课件 31页

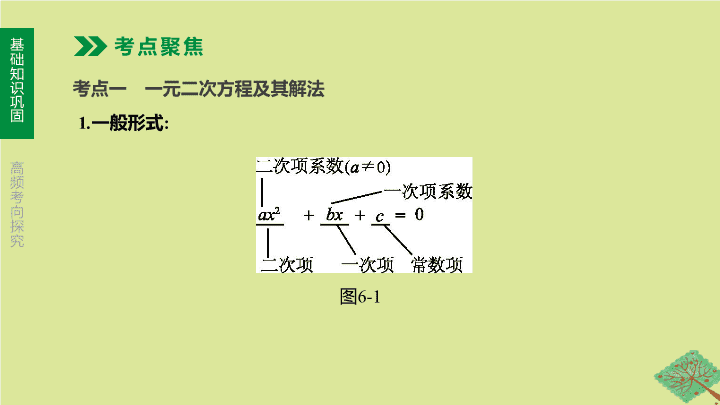
第 6 课时 一元二次方程及其应用 第二单元　方程 ( 组 ) 与不等式 ( 组 ) 【 考情分析 】 考点 2015 中考 相关题 2016 中考 相关题 2017 中考 相关题 2018 中考 相关题 2019 中考 相关题 2020 中考预测 一元二次方程的概念 ★★ 一元二次方程的解法 14 题 ,3 分 ★★★★★ 一元二次方程根的 判别式及根的情况 8 题 ,3 分 ★★★★ 一元二次方程的 根与系数的关系 一元二次方程的 应用 22 题 ,9 分 ★★★★★ 课本涉及内容 : 人教版九上第二十一章 P1-P26 . 考点一　一元二次方程及其解法 考点聚焦 1 . 一般形式 : 图 6-1 2 . 一元二次方程的解法 方法 解题流程 注意事项 直接开 平方法 (1) ax 2 + c =0 ⇒ x = ① 　　 　 ( 其中 ac< 0);  (2) a ( x + n ) 2 = b ⇒ x = ② 　　 ( 其中 ab> 0)  　 开方后取正负两个值 配方法 　 配方过程中 , 注意加上一个数的同时减去这个数 ( 续表 ) 方法 解题流程 注意事项 公式法 　 当 b 2 -4 ac ≥0 时 , 由求根公式可得 ax 2 + bx + c =0( a ≠0) 的解为 x = ③ 　 　　   　 前提条件 : ① 判别式 Δ ≥0; ② 等号的右边为 0 因式 分解法 　 ax 2 + bx + c =0( a ≠0) ( m 1 x + n 1 )·( m 2 x + n 2 )=0 ⇒ m 1 x + n 1 =0 或 m 2 x + n 2 =0, 求得 x 的值 　 当等号两边有相同的因式时 , 不能约去 , 以免漏解 考点二　一元二次方程根的判别式、根与系数的关系 1 . 判别式与根的关系 (1) b 2 -4 ac> 0⇔ 方程有 ④ 　 　 的实数根 ;(2) b 2 -4 ac =0⇔ 方程有 ⑤ 　　 　　 的实数根 ;  (3) b 2 -4 ac< 0⇔ 方程 ⑥ 　　　　 实数根 .  2 . 根与系数的关系 ( 选学 ) 若关于 x 的一元二次方程 ax 2 + bx + c =0( a ≠0) 的两根分别为 x 1 , x 2 , 则 x 1 + x 2 = ⑦ , x 1 x 2 = ⑧ 　　　　 .  两个不相等 两个相等 没有 考点三　一元二次方程的实际应用 应用类型 等量关系 增长率 问题 (1) 增长率 = 增量 ÷ 基础量 ; (2) 设 a 为原来的量 , m 为平均增长率 , n 为增长次数 , b 为增长后的量 , 则 a (1+ m ) n = b 销售利 润问题 (1) 纯利润 = 售出价 - 进货价 - 其他费用 ; (2) 利润率 = 利润 ÷ 进货价 ×100%; (3) 总利润 =( 售价 - 成本 )× 数量 ( 续表 ) 应用类型 等量关系 面积问题 AB + BC + CD = a S 阴影 = ⑨ 　   S 阴影 = ⑩ 　   S 阴影 = ⑪   ( a -2 x )( b -2 x ) ( a - x )( b - x ) 题组一　必会题 对点演练 1 . 若关于 x 的方程 ( m -1) x 2 + mx -1=0 是一元二次方程 , 则 m 的取值范围是 ( 　　 ) A .m ≠1 B .m =1 C .m ≥1 D .m ≠0 2 . 一元二次方程 x 2 -16=0 的根是 ( 　　 ) A .x =2 B .x =4 C .x 1 =2, x 2 =-2 D .x 1 =4, x 2 =-4 A D 3 . 用配方法解一元二次方程 x 2 -6 x -10=0 时 , 下列变形正确的是 ( 　　 ) A . ( x +3) 2 =1 B . ( x -3) 2 =1 C . ( x +3) 2 =19 D . ( x -3) 2 =19 4 . 方程 x 2 -2 x +3=0 的根的情况是 ( 　　 ) A . 有两个相等的实数根 B . 有两个不相等的实数根 C . 没有实数根 D . 无法确定 5 . 某公司 9 月份的利润为 100 万元 , 若要使 11 月份的利润达到 144 万元 , 则平均每月增长的百分率为 ( 　　 ) A . 10% B . 20% C . 22% D . 25% D C B 题组二　易错题 m ≤3 且 m ≠2 【 失分点 】 有关一元二次方程最易失分的地方一是解方程时 “ 丢根 ”, 二是运用根的判别式时忘记考虑二次项系数不为 0 的条件 . 6 . 一元二次方程 2 x ( x +1)=3( x +1) 的解是 　　　 　 .  7 . 若关于 x 的一元二次方程 ( m -2) x 2 +2 x +1=0 有实数根 , 则 m 的取值范围是 　　　 . 考向一　一元二次方程的解法 例 1 分别用公式法、配方法、分解因式法解一元二次方程 : x 2 -12 x +27=0 . 解法二 ( 配方法 ): 原方程为 x 2 -12 x +27=0, x 2 -12 x =-27, x 2 -12 x +6 2 =-27+6 2 , ( x -6) 2 =9, x -6=±3, ∴ x 1 =3, x 2 =9 . 解法三 ( 分解因式法 ): 原方程为 x 2 -12 x +27=0, ( x -3)( x -9)=0 . ∴ x -3=0 或 x -9=0 . ∴ x 1 =3, x 2 =9 . | 考向精练 | 1 . [2015· 鄂尔多斯 14 题 ] 小奇设计了一个魔术盒 , 当任意实数对 ( a , b ) 进入其中时 , 会得到一个新的实数 a 2 -3 b -5 . 例如 , 把 (1,-2) 放入其中 , 就会得到 1 2 -3×(-2)-5=2 . 现 将实数对 ( m ,3 m ) 放入其中 , 得到实数 5, 则 m = 　　 　　 .  10 或 -1 2 . [2017· 鄂尔多斯 17(1) 题节选 ] 解方程 : x ( x -1)=2 x -2 . 解 : x ( x -1)=2 x -2, x ( x -1)=2( x -1), x ( x -1)-2( x -1)=0,( x -1)( x -2)=0, ∴ x 1 =1, x 2 =2 . 考向二　一元二次方程根的判别式 例 2 已知关于 x 的一元二次方程 ( m -1) x 2 -(2 m +1) x + m =0 . (1) 当 m 取何值时 , 方程有两个不相等的实数根 ? (2) 当 m 取何值时 , 方程有两个相等的实数根 , 请求出根 . (3) 当 m 取何值时 , 方程没有实数根 ? 例 2 已知关于 x 的一元二次方程 ( m -1) x 2 -(2 m +1) x + m =0 . (2) 当 m 取何值时 , 方程有两个相等的实数根 , 请求出根 . 例 2 已知关于 x 的一元二次方程 ( m -1) x 2 -(2 m +1) x + m =0 . (3) 当 m 取何值时 , 方程没有实数根 ? | 考向精练 | D [ 答案 ] D 考向三　一元二次方程的应用 例 3 [2019· 东营 ] 为加快新旧动能转换 , 提高公司经济效益 , 某公司决定对近期研发出的一种电子产品进行降价促销 , 使生产的电子产品能够及时售出 , 根据市场调查 : 这种电子产品销售单价定为 200 元时 , 每天可售出 300 个 ; 若销售单价每降低 1 元 , 则每天可多售出 5 个 . 已知每个电子产品的固定成本为 100 元 , 问这种电子产品降价后的销售单价为多少元时 , 公司每天可获利 32000 元 ? 解 : 设降价后的销售单价为 x 元 , 根据题意得 : ( x -100)[300+5(200- x )]=32000 . 整理得 :( x -100)(1300-5 x )=32000, 即 x 2 -360 x +32400=0, 解得 x 1 = x 2 =180, x =180 < 200, 符合题意 . 答 : 这种电子产品降价后的销售单价为 180 元时 , 公司每天可获利 32000 元 . | 考向精练 | 1 . [2019· 邵阳 ] 2019 年 1 月 14 日 , 国新办举行新闻发布会 , 海关总署新闻发言人李魁文在会上指出 : 在 2018 年 , 我国进出口规模创历史新高 , 全年外贸进出口总值为 30 万亿元人民币 , 有望继续保持全球货物贸易第一大国地位 . 预计 2020 年我国外贸进出口总值将达 36 . 3 万亿元人民币 . 求这两年我国外贸进出口总值的年平均增长率 . 解 : 设这两年我国外贸进出口总值的年平均增长率为 x , 根据题意列方程得 30(1+ x ) 2 =36 . 3, 解得 x 1 =0 . 1=10%, x 2 =-2 . 1( 舍 ), 答 : 我国外贸进出口总值的年平均增长率为 10% . 2 . [2019· 南京 ] 某地计划对矩形广场进行扩建改造 . 如图 6-2, 原广场长 50 m, 宽 40 m, 要求扩充后的矩形广场长与宽的比为 3 ∶ 2 . 扩充区域的扩建费用为每平方米 30 元 , 扩建后在原广场和扩充区域都铺设地砖 , 铺设地砖费用为每平方米 100 元 . 如果计划总费用为 642000 元 , 扩充后广场的长和宽应分别是多少米 ? 图 6-2 解 : 设扩充后广场的长为 3 x m, 宽为 2 x m, 依题意得 :3 x ·2 x ·100+30(3 x ·2 x -50×40)=642000, 解得 x 1 =30, x 2 =-30( 舍去 ) . 所以 3 x =90,2 x =60, 答 : 扩充后广场的长为 90 m, 宽为 60 m . 考向四　创新题型 例 4 [2018· 黔西南州 ] “ 分块计数法 ”: 对有规律的图形进行计数时 , 有些题可以采用 “ 分块计数 ” 的方法 . 例如 , 图 6-3 ①有 6 个点 , 图②有 12 个点 , 图③有 18 个点 ,……, 按此规律 , 求图⑩ , 图 有多少个点 ? 我们将每个图形分成完全相同的 6 块 , 每块黑点的个数相同 ( 如图 6-4), 这样图①中黑点个数是 6×1=6 个 ; 图②中黑点个数是 6×2=12 个 ; 图③中黑点个数是 6×3=18 个 ;… 所以容易求出图⑩ , 图 中黑点的个数分别是 　　 　　 , 　　 .  图 6-3 图 6-4 请你参考以上 “ 分块计数法 ”, 先将下面的点阵进行分块 , 再完成以下问题 : (1) 第 5 个点阵中有 　　　　 个圆圈 ; 第 n 个点阵中有 　　　　 个圆圈 .  (2) 小圆圈的个数会等于 271 吗 ? 如果会 , 请求出是第几个点阵 . 图 6-5 解 : 图⑩中黑点个数是 6×10=60; 图 n ○ 中黑点个数是 6 n , 故答案为 60;6 n. 分块如下 ( 不唯一 ): (1) 如图 , 第 1 个点阵中有 1 个圆圈 , 第 2 个点阵中有 2×3+1=7( 个 ) 圆圈 , 第 3 个点阵中有 3×6+1=19( 个 ) 圆圈 , 第 4 个点阵中有 4×9+1=37( 个 ) 圆圈 , 第 5 个点阵中有 5×12+1=61( 个 ) 圆圈 ,…, 第 n 个点阵中有 n ×3( n -1)+1=3 n 2 -3 n +1( 个 ) 圆圈 , 故答案为 61;3 n 2 -3 n +1 . 例 4 [2018· 黔西南州 ] “ 分块计数法 ”: 对有规律的图形进行计数时 , 有些题可以采用 “ 分块计数 ” 的方法 . 例如 , 图 6-3 ①有 6 个点 , 图②有 12 个点 , 图③有 18 个点 ,……, 按此规律 , 求图⑩ , 图 有多少个点 ? 我们将每个图形分成完全相同的 6 块 , 每块黑点的个数相同 ( 如图 6-4), 这样图①中黑点个数是 6×1=6 个 ; 图②中黑点个数是 6×2=12 个 ; 图③中黑点个数是 6×3=18 个 ;… 所以容易求出图⑩ , 图 中黑点的个数分别是 　　 　　 , 　　 .  图 6-3 图 6-4 请你参考以上 “ 分块计数法 ”, 先将下面的点阵进行分块 , 再完成以下问题 : (2) 小圆圈的个数会等于 271 吗 ? 如果会 , 请求出是第几个点阵 . 图 6-5 解 : 图⑩中黑点个数是 6×10=60; 图 n ○ 中黑点个数是 6 n , 故答案为 60;6 n. 分块如下 ( 不唯一 ): (2) 会 . 3 n 2 -3 n +1=271, n 2 - n -90=0,( n -10)( n +9)=0, n 1 =10, n 2 =-9( 舍去 ), ∴小圆圈的个数会等于 271, 它是第 10 个点阵 .