中考数学复习专题十二：方程观点解几何计算题 8页

中考数学复习专题12 方程观点解几何计算题 概述： 含有未知数的等式便是方程，代数方面的应用题，几何方面的计算题便是求某些未知数的值，都可用方程的观点去解决，一般一个未知数列一个方程，两个未知数列两个方程． 典型例题精析 ‎ 例1．有一块直角三角形纸片，两直角边AC=‎6cm，BC=‎8cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，求CD长． ‎ 分析：Rt△ABC，∠C=90°，AC=6，BC=8 AB=10．由题意知 △ ACD≌△AED∠DEB=90°，DECD，AC=AE=6， ‎ 设CD=x，则DE=x，而EB=4， ‎ 一个未知数，需要一个方程，从何而来，图中有直角，用勾股定理，有等式，有方程． ‎ ∴在Rt△DEB中，（8-x）2=x2+42， ‎ 64-16x+x2=x2+16， ‎ 16x=48， x=3（cm）． ‎ 例2．已知⊙O中，两弦AB、CD相交于E，若E为AB中点，且CE：ED=1：4，AB=4，求CD长． ‎ 解：∵CE：ED=1：4， ‎ ∴设CE=x，则ED=4x，由相交弦定理得 ‎ CE·ED=AE·EB， ‎ 即x·4x=2×2， ‎ 4x2=4， x=1． ‎ ∴CD=x+4x=5x=5． ‎ 例3．如图，AB为⊙O的直径，P点在AB延长线上，PM切⊙O于M点，若OA=a，PM=a，求△PMB的周长． ‎ 分析：条件符合切割线定理，设BP=x，则由PM2=PB·PA（方程出来了） ‎ 得（a）2=x（x+‎2a）， ‎ x2+2ax‎-3a2=0， ‎ （x+‎3a）（x-a）=0， ‎ ∴x1=a，x2=‎-3a（舍去） ‎ ∴x=a，即BP=a，连结MO（常作辅助线） ‎ 则∠OMP=90°，∵OB=BP=a，则MB为Rt△OMP的斜边上的中线，∴MB=OP=a． ‎∴△MBP的周长为2a+a． ‎ 例4．如图，圆心在Rt△ABC斜边AB上的半圆切直角边AC、BC于M、N，其中AC=6，BC=8，求半圆的半径． ‎ ‎ ‎ 分析：设半径为R，（一个未知数建立一个方程即可），连OM、ON、OC， ‎ 则OM=ON=R，用面积，S△AOC+S△BOC=S△ABC， ‎ 得6R+8R=6×8（一元一次方程） ‎ 14R=48， R=． 中考样题训练: ‎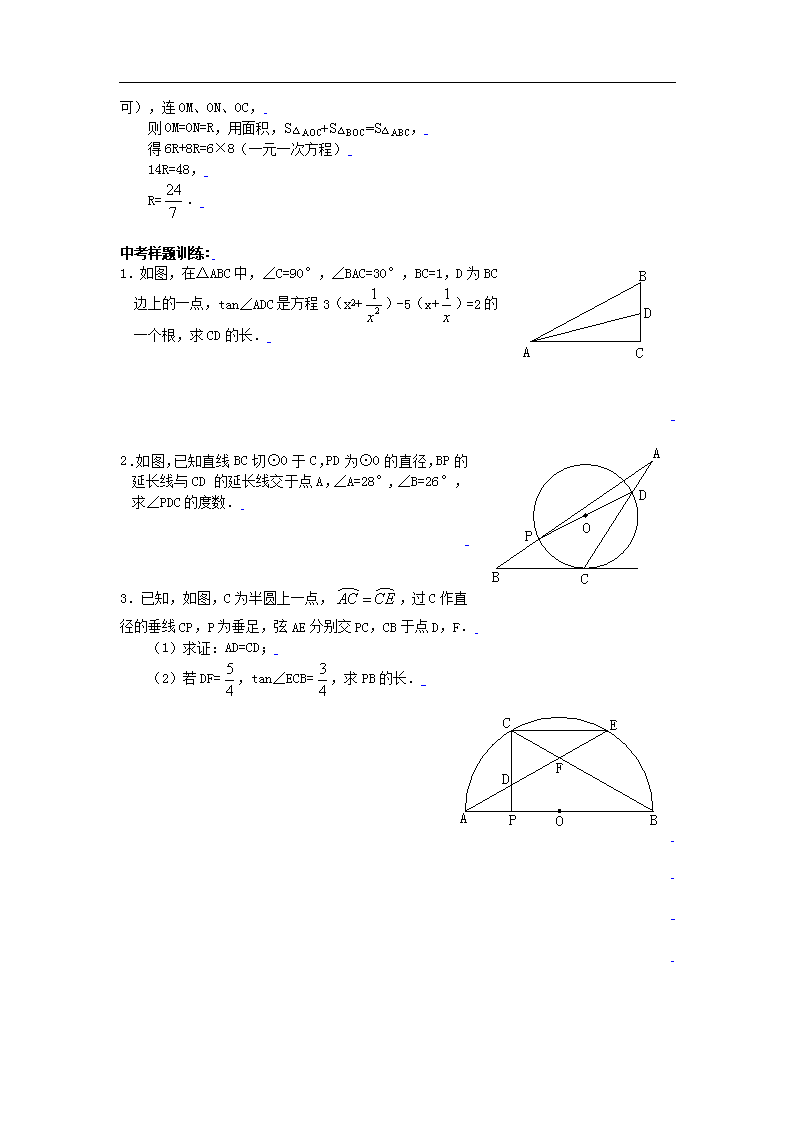1．如图，在△ABC中，∠C=90°，∠BAC=30°，BC=1，D为BC边上的一点，tan∠ADC是方程3（x2+）-5（x+）=2的一个根，求CD的长． ‎2．如图，已知直线BC切⊙O于C，PD为⊙O的直径，BP的延长线与CD的延长线交于点A，∠A=28°,∠B=26°，求∠PDC的度数． ‎3．已知，如图，C为半圆上一点，，过C作直径的垂线CP，P为垂足，弦AE分别交PC，CB于点D，F． ‎ （1）求证：AD=CD； ‎（2）若DF=，tan∠ECB=，求PB的长． ‎ 4．已知关于x的方程x2-（k+1）x+k2+1=0的两根是一个矩形两邻边的长． ‎ （1）k取何值时，方程有两个实数根； ‎（2）当矩形的对角线长为时，求k的值． ‎ 5．如图所示，AB是⊙O的直径，BC是⊙O的弦，⊙O的割线PDE垂直AB于点F，交BC于点G，连结PC，∠BAC=∠BCP，求解下列问题： ‎ （1）求证：CP是⊙O的切线； ‎ （2）当∠ABC=30°，BG=2，CG=4时，求以PD、PE的长为两根的一元二次方程． ‎（3）若（1）的条件不变，当点C在劣弧AD上运动时，应再具备什么条件可使结论BG2=BF·DO成立？试写出你的猜想，并说明理由．‎ ‎ 6．已知：如图所示，BC为⊙O的直径，AD⊥BC，垂足为D，弦BF和AD交于E，且AE=BE．‎ ‎ （1）试猜想：与有何大小关系？并证明你的猜想；‎ ‎ （2）若BD、CD的长是关于x的方程x2-kx+16=0的两个根，求BF的长；‎ ‎ （3）在（2）的条件下，若k为整数，且满足，求sin2∠A的值．‎ 考前热身训练 ‎1．要用圆形铁片截出边长为‎4cm的正方形铁片，求选用的圆形铁片的直径的最小值．‎ ‎2．圆内两条弦AB和CD相交于P点，AB长为7，AB把CD分成两部分的线段长为2和6，求AP的长．‎ ‎3．如图，PA切⊙O于点A，PBC交⊙O于B、C，若PB、PC的长是关于x的方程x2-（m-2）x+（m+2）=0的两个根，且BC=4，求m的值及PA的长．‎ ‎4．如图，D是△ABC的边AC上一点，CD=2AD，AE⊥BC，交BC于点E，若BD=8，sin∠CBD=，求AE的长．‎ ‎5．如图，在△ABC中，∠CAD=∠B，若AD=7，AB=8，AC=6，求DC的长．‎ ‎6．已知，如图，以△ABC的边BC为直径的半圆交AB于D，交AC于E，过E点作EF⊥BC，垂足为F，且BF：FC=5：1，AB=8，AE=2，求EC的长．‎ 答案:‎ 中考样题看台 ‎1．解：3（x+）2-5（x+）-8=0，‎ ‎ x+=或x+=-1，‎ ‎ 由x+=得x=．‎ ‎ x+=-1得x2+x+1=0无解．‎ ‎ ∴tan∠ADC=，‎ ‎ 在Rt△ABC中，AC==．‎ ‎ 在Rt△ADC中，CD==．‎ ‎ ∵CD<1，∴CD=．‎ ‎2．∠PDC=36°‎ ‎3．（1）证明：连结AC，∵，∴∠CEA=∠CAE．‎ ‎∵∠CEA=∠CBA，∴∠CBA=∠CAE，‎ ‎∵AB是直径，∴∠ACB=90°，‎ ‎∵CP⊥AB，∴∠CBA=∠ACP，‎ ‎∴∠CAE=∠ACP，∴AD=CD．‎ ‎ （2）解：∵∠ACB=90°，∠CAE=∠ACP，‎ ‎∴∠DCF=∠CFD，∴AD=CD=DF=，‎ ‎∵∠ECB=∠DAP，tan∠ECB=，∴tan∠DAP==，‎ ‎∵PD2+PA2=DA2，∴DP=，PA=1，∴CP=2，‎ ‎∵∠ACB=90°，CP⊥AB，∴△APC∽△CPB，∴，∴PB=4．‎ ‎4．（1）要使方程有两个实数根，必须△≥0，‎ ‎ 即[-（k+1）]2-4（k2+1）≥0，‎ ‎ 化简得：2k-3≥0，解之得：k≥．‎ ‎ （2） 解之得：k1=2，k2=-6‎ ‎ 由（1）可知，k=-6时，方程无实数根，所以，只能取k=2．‎ ‎5．（1）连结OC，证∠OCP=90°即可．‎ ‎ （2）∵∠B=30°，∠A=∠BCP=60°，‎ ‎ ∴∠BCP=∠CGP=60°，∴△CPG是正三角形．‎ ‎ ∴PG=CP=4，∴PC切⊙O于C．‎ ‎ ∴PC2=PD·PE=（4）2=48，‎ ‎ 又∵BC=6，∴AB=6，FD=3，EG=，‎ ‎ ∴PD=2，∴PD+PE=2+8=10．‎ ‎ ∴以PD、PE为两根的一元二次方程为x2-48x+10=0．‎ ‎ （3）当G为BC中点，OG⊥BC，OG∥AC或∠BOG=∠BAC…时，结论BG2=BF·BO成立．要让此结论成立，只证明△BFG∽△BGO即可，凡是能使△BFG∽△BGO的条件都可以．‎ ‎6．可以猜想到．‎ ‎ 证明：延工AD交⊙O于点G．‎ ‎ ∵BC是⊙O的直径，AD⊥BC，‎ ‎ ∴． ∵AE=BE，‎ ‎ ∴∠ABE=∠BAE，∴，∴．‎ ‎ （2）∵，∴，BF=AG．‎ ‎ ∵AD⊥BC，BC是⊙O直径，‎ ‎ ∴AG=2AD， ∴BF=2AD，‎ ‎ ∵BD、CD的长是方程x-kx+16=0的两个根，‎ ‎ ∴BD·CD=16．‎ ‎ 又AD2=BD·CD，∴AD2=16，AD=4，∴BF=8．‎ ‎ （3）连结CF解不等式组得：9