2019九年级数学上册 第22章 一元二次方程 22几何问题与行程问题与一元二次方程 7页

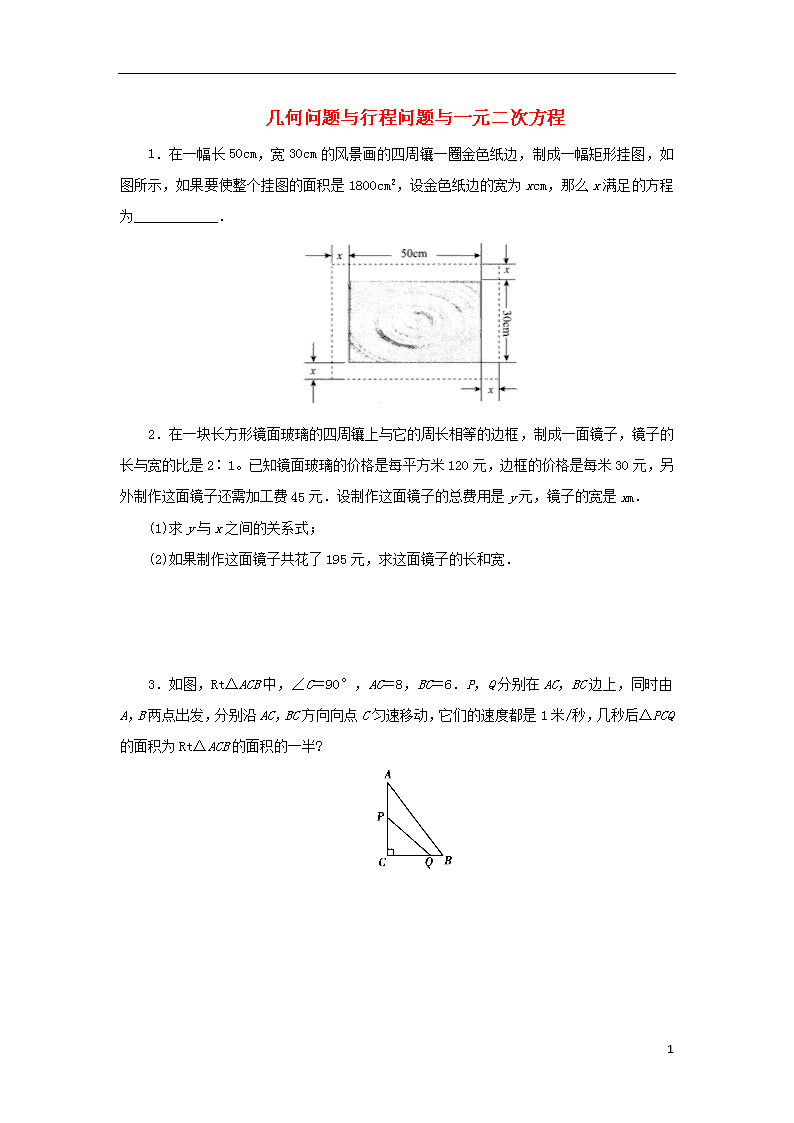
几何问题与行程问题与一元二次方程 ‎1．在一幅长‎50cm，宽‎30cm的风景画的四周镶一圈金色纸边，制成一幅矩形挂图，如图所示，如果要使整个挂图的面积是‎1800cm2，设金色纸边的宽为xcm，那么x满足的方程为____________．‎ ‎2．在一块长方形镜面玻璃的四周镶上与它的周长相等的边框，制成一面镜子，镜子的长与宽的比是2∶1。已知镜面玻璃的价格是每平方米120元，边框的价格是每米30元，另外制作这面镜子还需加工费45元．设制作这面镜子的总费用是y元，镜子的宽是xm．‎ ‎(1)求y与x之间的关系式；‎ ‎(2)如果制作这面镜子共花了195元，求这面镜子的长和宽．‎ ‎3．如图，Rt△ACB中，∠C＝90°，AC＝8，BC＝6．P，Q分别在AC，BC边上，同时由A，B两点出发，分别沿AC，BC方向向点C匀速移动，它们的速度都是‎1米/秒，几秒后△PCQ的面积为Rt△ACB的面积的一半?‎ 7‎ ‎4．如图，已知A，B，C，D为矩形的四个顶点，AB＝16厘米，AD＝6厘米．动点P，Q分别从A，C同时出发，点P以3厘米/秒的速度向点B移动，一直到点B为止，点Q以2厘米/秒的速度向D移动．当P，Q两点从出发开始到几秒时，点P，Q间的距离是‎10厘米?‎ ‎5.如图所示，在△ABC中，∠C＝90°，AC＝‎6cm，BC＝‎8cm，点P从点A出发沿边AC向点C以‎1cm/s的速度移动，点Q从点C出发沿CB边向点B以‎2cm/s的速度移动.‎ ‎（1）如果点P，点Q同时出发，那么几秒钟后，可使△PCQ的面积为8cm2？‎ ‎（2）点P，点Q在移动的过程中是否存在某一时刻，使得△PCQ的面积是△ABC面积的一半，若存在，求出t；若不存在，说明理由.‎ ‎6.李明准备进行如下操作实验：把一根长‎40cm的铁丝剪成两段，并把每段首尾相连各围成一个正方形.‎ ‎（1）要使这两个正方形的面积和等于58cm2，李明应该怎么剪这根铁丝？‎ ‎（2）李明认为这两个正方形的面积之和不可能等于48cm2.你认为他的说法正确吗？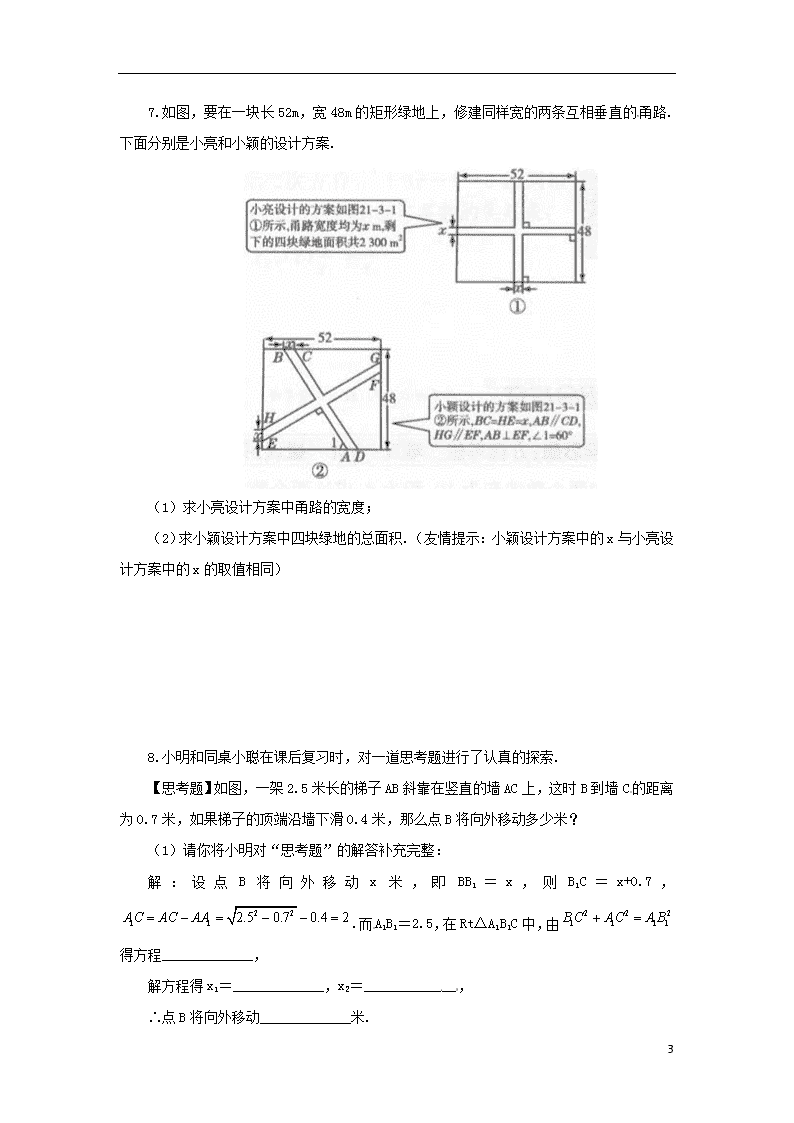请说明理由.‎ 7‎ ‎7.如图，要在一块长‎52m，宽‎48m的矩形绿地上，修建同样宽的两条互相垂直的甬路.下面分别是小亮和小颖的设计方案.‎ ‎（1）求小亮设计方案中甬路的宽度；‎ ‎（2）求小颖设计方案中四块绿地的总面积.（友情提示：小颖设计方案中的x与小亮设计方案中的x的取值相同）‎ ‎8.小明和同桌小聪在课后复习时，对一道思考题进行了认真的探索.‎ ‎【思考题】如图，一架2.5米长的梯子AB斜靠在竖直的墙AC上，这时B到墙C的距离为0.7米，如果梯子的顶端沿墙下滑0.4米，那么点B将向外移动多少米？‎ ‎（1）请你将小明对“思考题”的解答补充完整：‎ 解：设点B将向外移动x米，即BB1＝x，则B1C＝x+0.7，.而A1B1＝2.5，在Rt△A1B1C中，由得方程_____________，‎ 解方程得x1＝_____________，x2＝_____________，‎ ‎∴点B将向外移动_____________米.‎ 7‎ ‎（2）解完“思考题”后，小聪提出了如下两个问题：‎ ‎①在“思考题”中，将“下滑0.4米”改为“下滑0.9米”，那么该题的答案会是0.9米吗？为什么？‎ ‎②在“思考题”中，梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离，有可能相等吗？为什么？‎ 请你解答小聪提出的这两个问题.‎ ‎9.随着铁路客运量的不断增长，某地火车北站越来越拥挤，为了满足铁路交通的快速发展，该火车站从去年开始启动了扩建工程.其中某项工程，甲队单独完成所需时间比乙队单独完成需时间多5个月，并且两队单独完成所需时间的乘积恰好等于两队单独完成所需时间之和的6倍.‎ ‎（1）求甲、乙两队单独完成这项工程各需几个月.‎ ‎（2）若甲队每月的施工费为100万元，乙队每月的施工费比甲队多50万元.在保证工程质量的前提下，为了缩短工期，拟安排甲、乙两队分工合作完成这项工程.在完成这项工程中，甲队施工时间是乙队施工时间的2倍，那么，最多安排甲队施工几个月才能使工程款不超过1500万元？（甲、乙两队的施工时间按月取整数）‎ 7‎ 参考答案 ‎1．(50＋2x)(30＋2x)＝1800． ‎ ‎2．分析：(1)y＝240x2＋180x＋45；(2)y＝195时， (舍去)．‎ ‎∴这面镜子长为1m，宽为 ‎3．分析：设x秒后△PCQ的面积为△ACB的面积的一半．‎ 依题意， (舍)．‎ 即2秒后△PCQ的面积为Rt△ACB的面积的一半．‎ ‎4．分析：设P，Q两点开始出发到x秒时，P，Q距离为‎10cm．‎ ‎(16－3x－2x)2＝102－62．‎ ‎∴出发秒或秒时，点P，Q距离为‎10cm．‎ ‎5.解：（1）设ts后△PCQ的面积为‎8cm2，由题意得 ‎，‎ 即t2－6t+8＝0， ‎ 解得t1＝2，t2＝4，‎ 即2s或4s后△PCQ的面积为8cm2. ‎ ‎（2）由题意得，‎ 即t2－6t+12＝0，‎ ‎∆＝36－48＝－12<0，方程无解， ‎ 所以不存在这样的时刻，使得△PCQ的面积是△ABC面积的一半. ‎ ‎6.解：（1）设其中一个正方形的边长为xcm，则另一个正方形的边长为(10－x)cm，由题意得x2+(10－x)2＝58.‎ 解得x1＝3，x2＝7，‎ ‎∴这两个正方形的周长分别为4×3＝12（cm），4×7＝28（cm），‎ ‎∴李明应该把铁丝剪成12cm和28cm的两段.‎ ‎（2）李明的说法正确.设其中一个正方形的边长为ycm，则另一个正方形的边长为(10－y)cm，由题意得y2+(10－y)2＝48，整理得y2－10y+26＝0，‎ ‎∵∆＝(－10)2－4×1×26＝－4<0，‎ ‎∴此方程无实数根.即这两个正方形的面积之和不可能等于48cm2.∴‎ 7‎ 李明的说法是正确的.‎ ‎7.解：（1）根据小亮的设计方案列方程，得(52－x)(48－x)＝2300.‎ 解这个方程，得x1＝2，x2＝98（舍去）.‎ ‎∴小亮设计的方案中甬路的宽度为2m.‎ ‎（2）如图，作AI⊥CD，HJ⊥EF，垂足分别为I，J.‎ ‎∵AB∥CD，∠1＝60°，∴∠ADI＝60°.‎ ‎∵BC∥AD，‎ ‎∴四边形ADCB为平行四边形，‎ ‎∴BC＝AD．‎ 由（1）得x＝2，∴BC＝HE＝2m＝AD．‎ 在Rt△ADI中，利用勾股定理可得m.‎ 同理可得.‎ ‎∴小颖设计的方案中四块绿地的总面积为（m2）.‎ ‎8.思路建立 （1）要求出点B向外移动的距离，即求BB1的长，直接把B‎1C，A‎1C，A1B1的值代入进行解答即可.‎ ‎（2）把（1）中的0.4换成0.9可知原方程不成立；设梯子顶端从A处下滑x米，点B向外也移动x米，由题意列方程，根据求出x的值是否符合题意进行判断.‎ 解：（1）(x+0.7)2+22＝2.52‎ x=0.8或－2.2（舍去）故x=0.8‎ ‎（2）①不会是0.9米，‎ 若AA1＝BB1＝0.9，则A1C＝2.4－0.9＝1.5，B1C＝0.7+0.9＝1.6，1.52+1.62＝4.81，2.52＝6.25，‎ ‎∵A1C2+B1C2≠A1B12，‎ 7‎ ‎∴该题的答案不会是0.9米.‎ ‎②有可能.‎ 设梯子顶端从A处下滑x米，点B向外也移动x米，‎ 则有(x+0.7)2+(2.4－x)2＝2.52，‎ 解得x＝1.7或x＝0（舍）.‎ ‎∴当梯子顶端从A处下滑1.7米时，点B向外也移动1.7米，即梯子顶端从A处沿墙AC下滑的距离与点B向外移动的距离有可能相等.‎ ‎9.解：（1）设甲队单独完成这项工程需要x个月，‎ 则乙队单独完成这项工程需要(x－5)个月，由题意得x(x－5)＝6(x+x－5)，整理得x2－17x+30＝0.‎ 解得x1＝2，x2＝15，‎ x＝2不合题意，舍去，故x＝15，x－5＝10.‎ 答：甲队单独完成这项工程需要15个月，乙队单独完成这项工程需要10个月.‎ ‎（2）设在完成这项工程中甲队做了m个月，则乙队做了个月，由题意知，乙队每月的施工费为150万元，‎ 根据题意列不等式，得.‎ 解得.∵m为整数，∴m的最大值为8.‎ 答：最多安排甲队施工8个月才能使工程款不超过1500万元.‎ 7‎