二年级数学上册复习试题重点内容汇总 17页

北师大版二年级上册数学复习重点内容 第一单元 加与减 一、【数与代数】 1、数的运算。  100 以内数的连加、连减、加减混合运算;(书 P2—P6) (1) 运算： 连加：多个数字连续相加叫做连加。例如：28+24+23=85. 连减：多个数字连续相减叫做连减。例如：85-40-26=19. 加减混合：在运算中既有加法又有减法的运算。例如：67-25+28=70。 （2）连加、连减、混合(含加减)的三种运算，计算过程中建议分两 次计算：先计算出前两个数的结果，再将这个结果与第三个数进行运 算。为避免出错，在用竖式计算的过程中也建议用两个竖式计算。计 算过程中：相同数位对齐，从个位算起。 错误典型：被减数是 100，在连续退位的时候学生容易出错; 和是 100， 在连续进位的时候学生容易出错。 (2) 解决有关的简单实际问题： A、养成认真读题的习惯，借助用笔标注的方式来帮助自己分析，准 确判断是用加法算式还是减法算式来解决问题; B、正确计算并且带上正确的单位，最后写出答。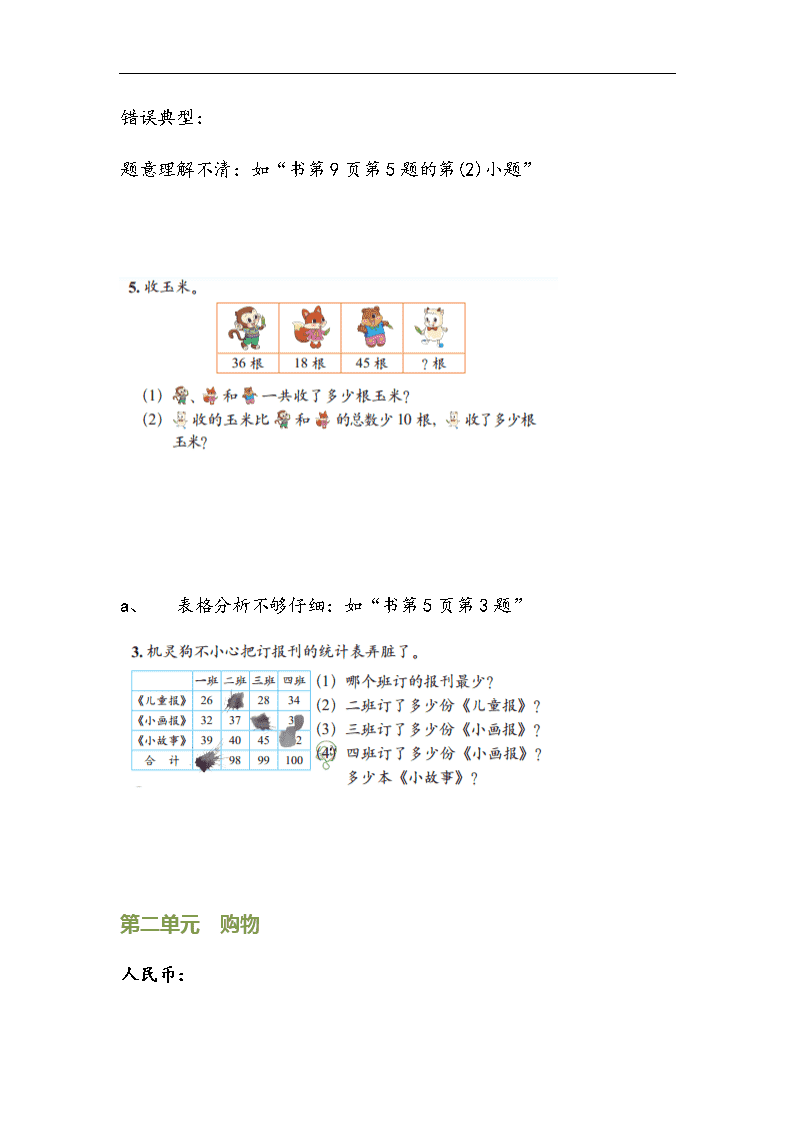 错误典型： 题意理解不清：如“书第 9 页第 5 题的第(2)小题” a、 表格分析不够仔细：如“书第 5 页第 3 题” 第二单元 购物 人民币： 我们国家的钱叫人民币，我们要爱护人民币。 1、人民币的单位有元、角、分。 2、1 元=10 角，1 角=10 分，1 元=100 分 3、元、角、分的加法计算：元和元相加，角和角相加，分和分相加， 满十分进一角，满十角进一元。例如 8 角+ 1 元 5 角=2 元 5 角 4、元、角、分的减法计算：元和元相减，角和角相减，分和分相减， 单位不同时，要统一单位后计算。 5、准确理解题意，抓住“正好”“不同”“几种”等关键词语理解题 意。解答后要注意验算。 人民币的认识 1、根据材质不一样可以分为纸币和硬币两类。 2、会认以小数形式表示的价格：小数点前面的数表示几元，小数点 后面第一位表示几角，小数点后第三位表示几分。 3、计算人民币时，单位名称相同时直接加减；单位名称不相同时， 要先进行换算成相同的再计算。 1 元=10 角 10 角=1 元 1 角=10 分 10 分=1 角 1 元=100 分 100 分=1 元 4、人民币比大小，先看元，元谁大，它就大：元相同在看角，角谁 大，它就大：角相同再看分，分谁大它就大。 5、最后的结果，要满 10 分进 1 角，满 10 角进 1 元。 6、元加元，角加角，元减元，角减角。（相同单位相加减） 7、单位名称相同时，可以直接计算：单位名称不同时，要先转化相 同单位名称，再计算。 8、1 元=100 分 几个 100 分就是几元。 9、1 角=10 分 几个 10 分就是几角。 10、元、角、分的认识。 1、人民币面额：1 分、2 分、五分 1 角、2 角、五角 1 元、2 元、五元 10 元、20 元、50 元、100 元 (学生会从人民币的大小、颜色、文字等方面去判断面额) 2、解决简单的实际问题 a、人民币兑换： (书 11 页第 1 题) b、算一算有多少钱： (书 11 页第 2 题) c、怎样付钱：（不要求列算式） (书 13 页第 1 题) 第三单元 数一数与乘法 3 × 4 ＝ 12 乘数 乘号 乘数 积 读作：3 乘 4 等于 12。 (1) 认识乘法算式并理解乘法的意义： 1、认识：乘数╳乘数=积 意义：表示几个相同加数相加的和。一定要加数相同才能写成乘法形 式 【例】6+6+6+6，是 4 个 6 相加，可以改写成 4×6 或者 6×4 2、加数不同的，先化成相同加数再改写。 8+8+8+8+4+4 改成乘法算式：8╳5 或 5╳8 或 10╳4 或 4╳10 【例】5+5+5+4，加数不相同，不能直接改写，如果要改，只能把“5+5+5” 的部分改写：5×3+4 3、乘法与加法的联系：如 3╳4=12 写成加法算式是：3+3+3+3=12 或 4+4+4=12; 3、3+3+3+3=12 写成乘法算式是：3╳4=12 或 4╳3=12。 4、在加法算式 8+8+8+8+8+8 中，相同的加数是 8。相同的加数的个 数是 6，写成乘法算式是 6╳8 或 8╳6 5、5 个 6 相加的加法算式：6+6+6+6+6+6 乘法算式 6╳5 或 5╳6 不能 5+5+5+5+5+5 7、乘法算式的读写顺序是从左往右。如 4 乘 5 只能写成 4╳5，不能 写成 5╳4，同样 2╳3 只能读作二乘三，不能读作三乘二。 4×6＝24 读作 4 乘 6 等于 24。读法中的乘号、等于号，读出来都要 用语文字表示。 8、乘法算式各部分的名称：因数×因数＝积。和加法算式一样，加 数交换位置，和不变。乘法算式中，因数交换位置，积不变。 9、解决相关的简单实际问题 （1）描述题意：要能够用比较准确的语言描述图意，才能正确地写 出乘法算式 描述范例：每架小飞机上有 2 个小朋友，有这样的 4 架 小飞机，就是 4 个 2，用 4×2 或 2×4 表示 （2）有图的题，或者给出加法算式的题，按照图意要能说出是几个 几。 （3）单一的乘法算式，可以表示两种含义。 【例】5×2，可以表 示 5 个 2 相加，就是 2+2+2+2+2，也可以表示 2 个 5 相加，就是 5+5。 （4）写算式。注意是要求写加法算式还是乘法算式。 【例】5 个 2 相加。用加法算式就是 2+2+2+2+2，用乘法算式就是 5×2 或 2×5。 如果题目没有说明，两种方法都可以。 (5) 虽然写着“相加”，但是相同加数相加就可以直接用乘法算式表 示。 【例】4 乘 6。写出来就是 4×6，题中给的是读法，因数不要交换位 置。 【例】4 和 6 相乘 / 求 4 和 6 的乘积 / 一个因数是 4，另一个因数 是 6。可以是 4×6，也可以是 6×4。习惯上我们按照题目中数字出 现的顺序写 4×6。（一个因数是 6，另一个因数是 4，就习惯上写 6 ×4） (6) 熟记表内乘法口诀：在理解的基础上熟记，会根据一个乘法口诀 推出另外的乘法口诀，如根据“三七二十一”可以推出“五七三十五” (7）个 7 比 3 个 7 多 2 个 7，也就是在 21 上再加 14，即 21+14=35。 （8）错误典型： a、“口诀”与“读作”混淆： 如：3╳7=21，读作：3 乘 7 等于 21。口诀：三七二十一(其中的“十” 字容易漏掉) b、算式与图形结合： 6、(书 79 页第 5 题) 7、 8、 9、 10、 11、(书 23 页第 4 题) 12、 13、 14、 15、(书 21 页第 1 题) 16、 17、 18、 19、 第四单元 图形的变化 1、图形的运动。（不要求纸笔测验） 2、初步感知轴对称现象 3、折一折，做一做：了解剪一个简单对称图形的操作步骤：对折— —画得像 20、 21、 22、 4、初步感知平移和旋转现象 a、在游戏中感受图形的平移与旋转的变化。 b、能够区别出物体运动的方式是平移还是旋转：平移物体在运动中 自身的方向不会变化。 c、能够在生活中找到物体平移和旋转运动的现象。 5、欣赏 6、欣赏轴对称图形在生活中的应用。 第五单元 2——5 的乘法口诀 乘法： 1、求几个几相加的和是多少，可以用乘法计算。 例： （1） 图中表示 3 个 4 相加，乘法算式是： 3×4=12 或 4×3=12 （2） 1 把 的单价是 6 元，买 3 把 需要多少元？ 算式是：3×6=18 （元）或 6×3=18（元） 2、求一个数的几倍是多少，也可以用乘法计算。 例：（1）小明今年 7 岁，爸爸的年龄是小明的 5 倍，爸爸今年多 少岁？ 算式是：5×7=35（岁） 或 7×5=35（岁） （2）香蕉有多少个？ 苹果： 香蕉： 算式是：5×3=15（个）或 3×5=15（个） 3、已知一个数是另一数的几倍，求一个数用乘法。 4、求一个数的几倍是多少用乘法。 5、解决间隔问题时，一定要先弄清楚共有多少个间隔，每个间隔的 距离是几，就是有几个几，用乘法计算。 6、锯木头时，次数+1=段数，段数-1=次数。锯的次数=段数-1 第六单元 测量 1、测量物体的长度，可以用厘米（cm）、米（m）作单位。 2、测量较短物体长度时，用厘米做单位比较合适；测量较长物体长 度时，用米做单位比较合适。 3、1 米=100 厘米 米可以用 m 表示 1m=100cm 4、一扎长大约 10 厘米 5、食指宽约 1 厘米 6、教室长 8 米 55 厘米 7、一米大约 5 只铅笔长 8、教室门宽约 1 米 9、测量之前要有统一的标准。 厘米是常用的长度单位，也可以写作 cm。通常，测量物体长度时，要把一段对准尺子的 0 刻度。 10、1 米=3 尺 1 尺=10 寸 1 米=30 寸 11、画线段注意： 1，画直线 2，直线两端有点 3， 标上几厘米 b、在测量的时候注意观察是否从尺子的“0”刻度开始，如果是从“0”刻度开始测量，则 可以直接读出物体的长度;如果不是从“0”刻度开始测量，物体的长度可以通过数格子 (即一个大格子就是一厘米)或是用物体末端对准的数减去起点对准的数，如： 常用的“相邻”的长度单位之间的进率是“10”，“相隔” 1 个长度单位之间的进率是“100”，“相隔”2 个长度单 位之间的进率是“1000”。我们又从中导出了 7 个单位转 换的公式分别是： 1 米=10 分米 1m=10dm 1 分米=10 厘米 1dm=10cm 1 厘米=10 毫米 1cm=10mm 1 米=100 厘米 1m=100cm 1 分米=100 毫米 1dm=100mm 1 米=1000 毫米 1m=1000mm 1 千米=1000 米 1km=1000m 27、我们还学习了 1 厘米中有（10）个小格，每小格的长 是 1 毫米。 1 分米大约有手掌这么长。1 分硬币大约有 1 毫米厚。 在表示较远的距离时，用“千米”作单位。 5、长度单位： 千米、 米、 分米、 厘米、 毫米。 用字母表示是： km、 m、 dm、 cm、 mm 。 第七单元 分一分与除法 12 ÷ 4 ＝ 3 被除数 除号 除数 商 读作：12 除以 4 等于 3。 总数 ÷每份数 = 份数 总数 ÷ 份数 = 每份数 一倍数 × 倍数 = 几倍数 几倍数 ÷ 倍数 = 1 倍数 第八单元：6—9 的乘法口诀 第九单元 除法 除法： 1、 平均分就是要分得一样多。 2、平均分有两种情况： ①平均分成几份。 例：平均每袋装（ ）个篮球。 算式： 12÷3=4（个） ②每几个分一份。 例：把下面的苹果分给小朋友，每个小朋友分得 2 个，可以分 给（ ）个小朋友。 算式： 12÷2=6（个） 3、把一些物品平均分，我们可以用除法计算。 4、求一个数是另一个数的几倍，可以用除法计算。 例： 3 元 12 元 的单价是 的几倍？ 算式是：12÷3=4 2、除法的三种含义：⑴表示：把一个数平均分成几份，每 份是几。（平均除法的意义）⑵表示：一个数里面有几个 几。（包含除法的意义）⑶表示：一个数是另一个数的几 倍。（倍数除法的意义） 3、求一个数是另一个数的几倍用除法。 5、已知一个数是另一数的几倍，求另一个数用除法。   除法的认识和用口诀求商 (1) 除法的意义 能够结合算式说出除法的意义，如算式 21÷3=7 可以表示： a、把 21 平均分成 3 份，每份是 7; b、把 21 拿来分，每份是 3，可以分成 7 份; c、 21 是 3 的 7 倍。 体会除法与乘法的“互逆”。 (2) 除法算式各部分的名称： 被除数÷除数=商 (了解：被除数÷商=除数 商╳除数=被除数) (3) 会用乘法口诀求出除法的商： 同样一句乘法口诀一般可以写出四个算式，两个乘法算式，两个除法算式。 如：三九二十七：3╳9=27 9╳3=27 27÷3=9 27÷9=3 (4) 理解“倍”和“倍数”的意义： 倍：是两个数之间的关系，可以用学生的话来理解——“大数里边有几个小数那么多”。 倍数：学生的话——“一个数的倍数就是这个数一个那么多、两个那么多、三个那么多…… 的数”，比如 3 的倍数是 3、6、9、12、15…… (5) 解决有关的简单实际问题： 认真读题，仔细分析。 错误典型： a、求“每份有多少”和“有多少份”的单位容易混淆： (书 66 页第 1 题) 纽扣题：求的是有多少份（单位：件）；苹果题：求得是每份有多少个（单位：个）。 b、 和“倍”相关的问题： 学生容易在选择用“乘法”还是“除法”来解决问题的时候混淆。 c、提一个生活中有关除法的问题。