北师大（2014秋）三年级上册数学试题-提升爬坡题（含解析） 35页

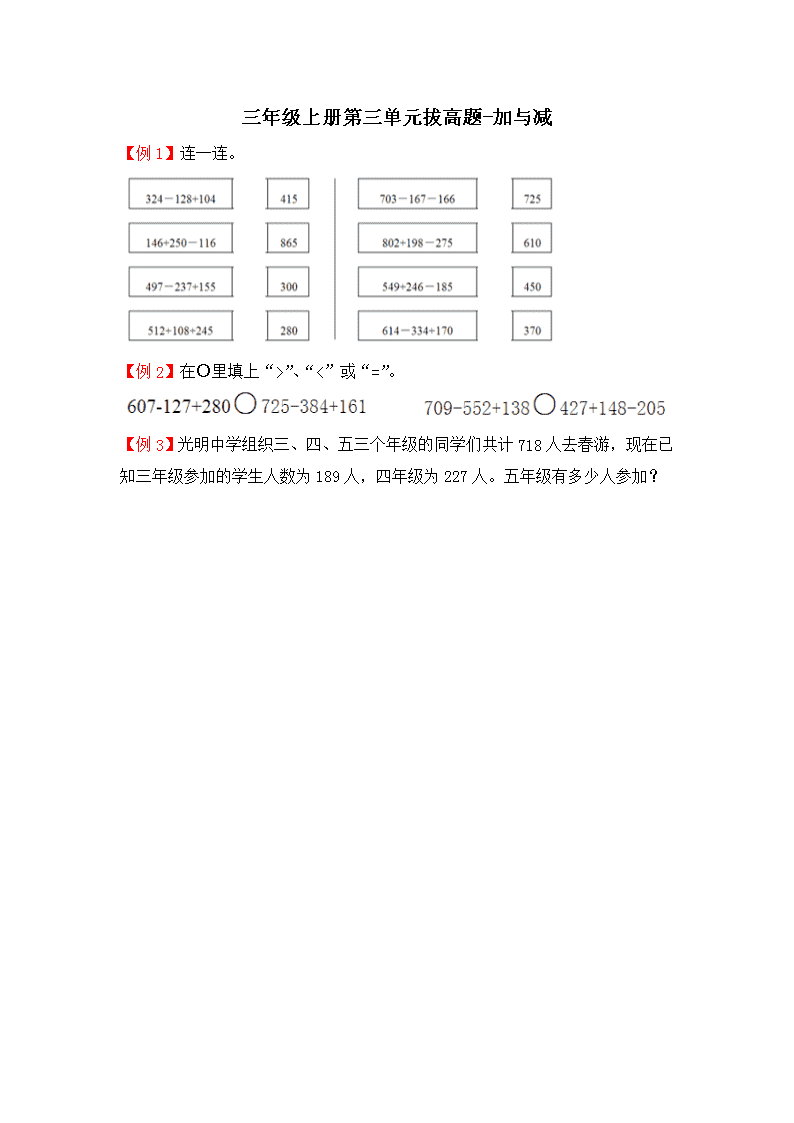
三年级上册第三单元拔高题-加与减 【例 1】连一连。 【例 2】在○里填上“>”、“<”或“=”。 【例 3】光明中学组织三、四、五三个年级的同学们共计 718 人去春游，现在已 知三年级参加的学生人数为 189 人，四年级为 227 人。五年级有多少人参加？ 三年级上册第三单元拔高题-加与减 参考答案 【例 1】连一连。 解析： 先把每个综合算式的得数计算出来，再把算式和相应 的得数直尺连线。如：324-128+104，先把前两个数字 相减 324-128，求出差是 196；再把得数 196 和第三个 数字相加 196+104，求出和是 300；故把算式 324-128+104 和数字 300 直尺连线。 解答： 【例 2】在○里填上“>”、“<”或“=”。 解析： 第一组算式 607-127+280○725-384+161，先分别 ○两边算式的得数，左边 607-127+280，先算 607-127， 差是 480，再算 480+280，求出和是 760；右边 725-384+161， 要点提示： 在只有加减法的混合运算 中，按照从左往右的顺序依 次进行计算。 要点提示： 先计算出每个算式的得数， 再比较大小。 先算 725-384，求出差是 341，再算 341+161，求出和是 502； 最后比较大小 760>502，也就是 607-127+280> 725-384+161，故○中应填>。 解答： >< 【例 3】光明中学组织三、四、五三个年级的同学们共计 718 人去春游，现在已 知三年级参加的学生人数为 189 人，四年级为 227 人。五年级有多少人参加？ 解析： 已知光明中学组织三、四、五三个年级的同学们共计 718 人去春游，现在已知三年级参加的学生人数为 189 人， 四年级为 227 人，求五年级有多少人参加。也就是用总人 数依次减去三年级和四年级参加的学生人数，列式为 718-189-227。计算时可以脱式计算，也可以竖式计算。 解答： 718-189-227 =529-227 =302（人）[来源:学科网 ZXXK] 答：五年级有 302 人参加. 三年级上册第四单元拔高题-乘与除 【例 1】算一算。 【例 2】整十数乘一位数且积是 240 的 乘法算式，你能写出多少个？ 【例 3】在校庆文艺体操表演中，三年级一共有 80 名同学参加，每 4 人分成一 要点提示： 竖式计算加减法时，注意相 同数位要对齐。 组，一共分成了多少组？ 【例 4】一个工厂，有男职工 200 人，女职工的人数是男职工的 4 倍，这个工厂 共有职工多少人？ 【例 5】猜猜每种图形代表哪一个整十数。 ○×3=1○ □×6=3□ 三年级上册第四单元拔高题-乘与除 参考答案 【例 1】算一算。 解析： 两位数乘（除）一位数的口算方法：先把两位数分成几个 要点提示： 整十、整百数乘（除）一位数的口 算方法：可以用因数中 0 前面的数 和一位数相乘（除），再看因数末 尾有几个 0，有几个 0 就在积（或 商）的末尾添上几个 0。 十和几个一，再分别与一位数相乘（除），最后把得到的 两个积（商）相加。如 13×3，先算 10×3=30，3×3=9， 再算 30+9=39，所以 13×3=39；36÷3，先算 30÷3=10， 6÷3=2，再算 10+2=12，所以 36÷3=12. 解答： . 【例 2】整十数乘一位数且积是 240 的 乘法算式，你能写出多少个？ 解析： 因为要写的算式是整十数乘一位数且积是 240，只要 运用表内乘法，找出积是 24 的两个数，然后把两个 因数中的一个写成整十数就可以了。积是 24 的口诀 有两句，在其中一个因数末尾加上 0，每句口诀都有 两种写法，共能写出 4 道算式。 解答： 30×8=240 80×3=240 40×6=240 60×4=240 【例 3】在校庆文艺体操表演中，三年级一共有 80 名同学参加，每 4 人分成一 组，一共分成了多少组？ 解析： 已知在校庆文艺体操表演中，三年级一共有 80 名同学 参加，每 4 人分成一组，求一共分成了几组，应该用 除法计算，列式为 80÷4.在口算 80÷4 的得数时，可以把 80 看作 8 个十，8 个十除以 4 就是 2 个十，即 80÷4=20. 解答： 要点提示： 熟练掌握表内乘法是解决 此类问题的关键。 要点提示： 口算除法不要急，先想乘法 再做除。利用表内除法算， 末尾添 0 要数清。 80÷4=20（组） 答：一共分成了 20 组. 【例 4】一个工厂，有男职工 200 人，女职工的人数是男职工的 4 倍，这个工厂 共有职工多少人？ 解析： 一个工厂，有男职工 200 人，女职工的人数是男职工 的 4 倍，求这个工厂共有职工总人数。先求出这个工厂 女职工人数，也就是 4 个 200 是多少，选择乘法列式 计算，列式为 200×4，在口算 200×4 的得数时，可以把 200 看作 2 个百，2 个百乘 4 就是 8 个百，即 200×4=800； 再求职工总人数，女职工人数+男职工人数=职工总人数，列式为 800+200，求出 和是 1000；列成综合算式为 200×4+200. 解答： 200×4+200 =800+200 =1000（人）答：这个工厂共有职工 1000 人. 【例 5】猜猜每种图形代表哪一个整十数。 ○×3=1○ □×6=3□ 解析： 运用表内乘法进行整十数乘一位数的口算，一个整十数 与 3 相乘，得到一个三位数，百位是 1，其他各位仍是 这个整十数。解答时可以一个一个地试，还可以把积 看作 100 加这个数，等号前面的算式可以看作 3 个这样的数相加，等号两边都减 去一个这个数，这个算式就可以写成○+○=100，所以○=50 .另一个算式解答方 法同第一个。 解答： 50×3=150 ○=50； 60×6=360 □=60. 三年级上册第五单元拔高题-周长 要点提示： 求一个数的几倍是多少，选 择乘法列式计算。 要点提示： 相同的图形表示的数相同。 【例 1】用笔描出下面各图形的周长。 【例 2】完成下面的表格（单位：厘米）。 【例 3】计算下面图形的周长。 【例 4】数一数下面图形的周长是多少厘米，再画一个边长是 3 厘米的正方形。 （每个小正方形边长 1 厘米）。 【例 5】淘气用一根长 36 厘米的铁丝围成一个最大的正方形，这个正方形的边 长 是多少厘米？ 【例 6】一块长方形菜地，长 6 米，宽 3 米。四周围上篱笆，篱笆长多少米？如 果一面靠墙，篱笆至少要多少米？[来源:学*科*网 Z*X*X*K] 三年级上册第五单元拔高题-周长 参考答案 【例 1】用笔描出下面各图形的周长。 解析： 给出的这些图形都是平面图形，又都是封闭图形，在 各个图形的边缘找一点，由这一点起沿边缘画一周， 再回到起点，是各个图形的周长。 解答： 【例 2】完成下面的表格（单位：厘米）。 解析： （1）长方形的周长就是要把长方形四条边加起来，但是 长方形的对边是相等的，所以我们只要知道长方形相邻 两边的长度即可，用公式“长方形的周长=（长+宽）×2” 来计算。 （2）正方形的周长就是正方形四条边的长度总和。根据正方形的四条边相等， 可以把四条边的边长加起来，也可以用一条边的长度乘 4，即正方形的周长=边 长×4. 要点提示： 每个图形所画线的长度是 这个图形一周的长度，即周 长。 要点提示： 长方形的对边相等， 正方形的四条边相等。 解答： 【例 3】计算下面图形的周长。 解析： 把每个图形各个边长相加就是每个图形的周长。 如：从左往右第二个图形，四条边长分别为 18 分米、 19 分米、16 分米和 14 分米，求它的周长，也就是把 这四条边的长度加在一起，列式为 18+19+16+14，求出[来源:学科网 ZXXK] 得数是 67；第三个图形看起来是个不规则图形的周长， 也就是要把所有的边长都加起来。通过平移图形中曲折的部分，正好可以拼成一 个长 10 厘米 、宽 8 厘米的长方形。利用长方形周长=（长+宽）×2，求出它的 周长。 解答： 21+23+27=71（厘米） 18+19+16+14=67（分米） （8+10）×2=36（厘米）. 【例 4】数一数下面图形的周长是多少厘米，再画一个边长是 3 厘米的正方形。 （每个小正方形边长 1 厘米）。 要点提示： 封闭图形一周的长度，是它 的周长。 解析： 根据题意可知：先数出每个图形的周长，再画出一个 边长是 3 厘米的正方形。数每个图形的周长时，可以 一个一个地数小正方形边长的个数，有多少个小正方形的 边长就有多少厘米，也可以先把两个不规则图形，通过 平移成规则图形，再求周长；画边长是 3 厘米的正方形，也就是画出边长是 3 个小正方形边长的正方形。 解答： 【例 5】淘气用一根长 36 厘米的铁丝围成一个最大的正方形，这个正方形的边 长 是多少厘米？ 解析： 根据题意可以知道：淘气用一根长 36 厘米的铁丝围成 一个最大的正方形，求这个正方形的边长，也就是 把 36 厘米的铁丝平均分成 4 份，求每份的长度，选择 除法列式计算，列式为 36÷4，求出商是 9，故这个正方形的边长是 9 厘米。 解答： 36÷4=9（厘米） 答：这个正方形的边长是 9 厘米. 【例 6】一块长方形菜地，长 6 米，宽 3 米。四周围上篱笆，篱笆长多少米？如 果一面靠墙，篱笆至少要多少米？[来源:学*科*网 Z*X*X*K] 要点提示： 正方形的四条边都相等， 四个角都是直角。 要点提示： 正方形的周长=边长×4。 解析： 把一块长 6 米，宽 3 米的长方形菜地，四周围上篱笆， 求篱笆的长度。根据长方形的周长计算公式，可以求出 篱笆的长度，是（6+3）×2。如果一面靠墙，求篱笆 至少要多少米，也就是长方形菜地的长靠墙时，此时需要的篱笆最短，是两个宽 的长度加一个长的长度，列式为 6+3×2. 解答： （6+3）×2=18（米） 6+3×2=12（米） 答 ：篱笆长 18 米，篱笆至少要 12 米. 三年级上册第一单元拔高题-混合运算 【例 1】下面的计算对吗？对的打“√”，错的打“×”，并把错的改正过来。 【例 2】想一想，填一填。 要点提示： 长方形的周长=（长+宽）×2。 【例 3】想一想，下面的小动物各代表数字几。 【例 4】小 灰钓了多少条鱼？ 三年级上册第一单元拔高题-混合运算 参考答案 【例 1】下面的计算对吗？对的打“√”，错的打“×”，并把错的改正过来。 解析： 在没有小括号的混合运算中，要先算乘除法，再算加减法； 在计算含有小括号的混合运算时，要先算小括号厘米的， 再算小括号外面的。 解答： 要点提示： 小括号的作用就是改变 运算顺序。 【例 2】想一想，填一填。 解析： 根据题意可以知道：先计算出每个算式的得数，再尝试 着把两个算式合并成一个算式。把两个算式合并成一个 算式，首先根据第一个算式的得数，把算式代入第二个 算式；然后根据混合运算的顺序判断是否需要加括号。 如：第一个计算 5+7 的和是 12，12÷3，商是 4，把算式 5+7 替换第二个算式中 的 12，列综合算式 5+7÷3，按照混合运算的顺序，先算除法，后算加法，和原 来的运算顺序就不一致了，所以要用小括号把 5+7 括起来，列式为（5+7）÷3. 解答： 【例 3】想一想，下面的小动物各代表数字几。 要点提示： 列综合算式时，要根据计算 的先后顺序加小括号。 解析： ① ，求 。 也就是（ ）+27-19=36，则（ ）=36+19-27，求出得数 是 28. ② ，求 。先求出小括号里 的和， =91-47=44，再利用 44-18，求出小鸭子代表的数字。 ③4×7-5，先算 4×7 的积是 28，再算 28-5 的差是 23，所以小乌龟代表的数字 是 23. ④ ，求 。先求出小括号里 的差， =72-29=43，则小象=63-43，求出差是 20. 解答： ①28②26③23④20. 【例 4】小 灰钓了多少条鱼？ 要点提示： 运用逆推思路是解决此类 问题的关键。 解析： 小黑有 9 条金鱼，小白钓的鱼是小黑的 4 倍，小灰比 小白多钓 26 条，求 小灰钓了多少条鱼。先求出小白 钓的鱼的条数，也就是 4 个 9 相加的和，列式为 9×4； 再求出小灰钓的鱼的条数，小白钓的鱼的条数+26= 小灰钓的鱼的条数，即 9×4+26；计算时，先算 9×4=36，再算 36+26=62. 解答： 9×4+26=62（条） 答：小灰钓了 62 条鱼。 三年级上册第八单元拔高题-认识小数 【例 1】看图填空。 【例 2】换算成以“元”为单位的小数。 4 元 5 角=（ ）元 2 元 8 分=（ ）元 要点提示： 解决问题时，先要根据问题 分析数量关系。 8 元 8 角 8 分=（ ）元 2 角 5 分=（ ）元 【例 3】比较大小。 【例 4】一个笔筒 5.6 元，一个削笔刀 2.9 元，一本日记本 8.5 元。淘淘带了 18 元 9 分。 （1） 买一个笔筒和一个削笔刀需要多少钱？ （2）他剩下的钱够不够买日记 本？ 三年级上册第八单元拔高题-认识小数 参考答案 【例 1】看图填空。 解析： 8.50 元，整数部分是 8，表示 8 元，小数点后面第一位 小数是 5 表示 5 角，第二位小数 0 表示 0 分； 6.55 元，整数部分是 6 表示 6 元，小数点后面第一位 小数是 5 表示 5 角，第二位小数 5 表示 5 分； 5.08 元，整数部分是 5 表示 5 元，小数点后面第一位 小数是 0 表示 0 角，第二位小数 8 表示 8 分； 0.82 元，整数部分是 0 表示 0 元，小数点后面第一位小数是 8 表示 8 角，第二 位小数 2 表示 2 分。 解答： 8 元 5 角 0 分 6 元 5 角 5 分 5 元 0 角 8 分 0 元 8 角 2 分. 【例 2】换算成以“元”为单位的小数。 4 元 5 角=（ ）元 2 元 8 分=（ ）元 8 元 8 角 8 分=（ ）元 2 角 5 分=（ ）元 解析： 根据 1 元=10 角，1 元=100 分，可以知道 1 角=0.1 元， 1 分=0.01 元。4 元 5 角是 4 元加 5 个 0.1 元是 4.5 元； 2 元 8 分是 2 元加 8 个 0.01 元是 2.08 元；8 元 8 角 8 分 是 8 元加 8 个 0.1 元加 8 个 0.01 元是 8.88 元；2 角 5 分 是 2 个 0.1 元加上 5 个 0.01 元是 0.25 元。 解答： 4.5 2.08 8.88 0.25. 【例 3】比较大小。 解析： 首先统一单位，可以把所有数量统一用元作单位，那么 5 元、5 角、1 角合起来是 5.6 元，5 元、5 角、1 分合 起来是 5.51 元，再比较 5.6 元和 5.51 元的大小，比较 小数的大小时，先比较整数部分，整数部分相等都是 5， 要点提示： 当用小数表示商品的价钱时，整数 部分表示的是几元，小数点后面第 一位小数表示几角，第二位小数表 示几分。 要点提示： 小数点要写成“.”，不要写 成“、”或“。”。 要点提示： 先分别求出每组的总钱数， 再比较大小。 再比较小数部分，先比较十分位上的小数 6 大于 5，故 5.6 元>5.51 元。同样的 方法比较用小组记录下一组人民币并比较大小。 解答： 5.6 元> 5.51 元 11.6 元< 12 元. 【例 4】一个笔筒 5.6 元，一个削笔刀 2.9 元，一本日记本 8.5 元。淘淘带了 18 元 9 分。 （1）买一个笔筒和一个削笔刀需要多少钱？ （2）他剩下的钱够不够买日记本？ 解析： （1）求买一个笔筒和一个削笔刀需要的钱数，就是求 5.6 元和 2.9 元的和是多少，用加法列式计算，列式为 5.6+2.9。 （2）求剩下的钱够不够买日记本，先求出剩下的钱， 再和一本笔记本的价钱 8.5 元作比较。 解答： （1）5.6+2.9=8.5（元） （2）18 元 9 分=18.09 元 18.09-8.5=9.59 元 9.59> 8.5 答：买一个笔筒和一个削笔刀 答：他剩下的钱够买日记本。 需要 8.5 元. 三年级上册第二单元拔高题-观察物体 【例 1】下面右边的图形分别是谁看到的？连一连。 【例 2】 要点提示： 列竖式时，元与元所在的数位对 齐，角与角所在的数位对齐，分与 分所在的数位对齐，这样就做到了 相同数位对齐。 【例 3】下面右边的图形分别是谁看到的？连一连。 三年级上册第二单元拔高题-观察物体 参考答案 【例 1】下面右边的图形分别是谁看到的？连一连。 解析： 老师和小女孩、小男孩看的都是同一张讲桌，但他们 要点提示： 从不同位置观察同一物体， 所看到的形状是不同的。 观察的位置是不同的。小女孩站在讲桌的左面，她看到 的是从左往右第三幅图；小男孩站在讲桌的右侧面，他 看到的是从左往右第 2 幅图；老师站在讲台上，她看到 的是讲桌的上面，是从左往右第一幅图。 解答： . 【例 2】 解析： 观察物体时，眼睛要直视所观察物体的面； 从正面看情景图，可以看到左面是长方形，右面是圆； 从右面看，可以看到圆和长方形重合并且长方形大于圆； 从左面看，长方体挡住了球，故只能看到所对的 长方体的一个面，也就是长方形。 解答： . 要点提示： 要分辨出看到的是什么图 形，关键是要弄清楚站在哪 一面。 【例 3】下面右边的图形分别是谁看到的？连一连。 解析： 头上扎蝴蝶结的小女孩站在情景图的正面，也就是从 前面观察物体，看到的是两行摆放的正方形，其中 从上往下第一行左侧摆放一个正方形，第二行左侧 和右侧均摆放一个正方形；另一个小女孩站在情景图 的右面，也就是从右面观察物体，看到的是竖直摆放的 两个正方形。 解答：[来] 三年级上册第九单元拔高题-总复习 【例 1】 学校里买来一些菊花，如果每行摆 6 盆，可以摆 4 行；如果每行摆 3 盆，可以摆几行？ 【例 2】生活中的数学。 要点提示： 从不同方向观察正方体，看 到的均是正方形。 【例 3】在下面的四幅图的括号中写上小朋友的名字。 【例 4】把 211、212、213、214 这四个数填入框中，使等式成立。 □+□-□=□ 【例 5】欢乐剧场的观众席分 A、B、C 三个区，A 区有 244 个座位，B 区有 228 个座 位，C 区比 A、B 两区的总和少 122 个座位，欢乐剧场一共能容纳多少名观 众？ 【例 6】动脑筋。 已知△+○=□，△+○+□=60，那么□=（ ）。 【例 7】要把一个长 9 厘米，宽 7 厘米的长方形剪成一个最大的正方形，剪去的 长方形的周长是多少厘米？ 【例 8】请把 2、4、5、0 这四个数填入□里，要使积最大，应该怎样填？ □□□×□ 【例 9】一列火车 6 时从甲站开出，15 时到达乙站。这列火车平均每小时行 150 千米，甲、乙两站相距多少千米？ 【例 10】一桶油，连桶共重 138.4 千克，连桶用去一半后，剩下的油连桶重 75.5 千克，油桶重多少千克？ 三年级上册第九单元拔高题-总复习 参考答案 【例 1】学校里买来一些菊花，如果每行摆 6 盆，可以摆 4 行；如果每行摆 3 盆， 可以摆几行？ 解析： 根据题意可知：学校里买来一些菊花，如果每行摆 6 盆，可以摆 4 行；如果每行摆 3 盆，求可以摆几行。 要点提示： 一个问题需要多个步骤解 决时，要想好先解答什么， 再解答什么。 不论如何摆放花盆，花盆的总数量是不变的，先求出 摆放花盆的总数量，每行摆的花盆数量 6×摆的行数 4 =摆放花盆总数量，列式为 6×4；再求出可以摆几行，[来源:Zxxk.Com] 也就是 6×4 里面有几个 3，选择除法列式计算，列式为 6×4÷3；计算时按照从 左往右的顺序依次进行计算，先算 6×4=24，再算 24÷3=8. 解答： 6×4÷3=8（行） 答：可以摆 8 行. 【例 2】生活中的数学。 解析： （1）每听可口可乐 4 元，李叔叔买了 8 听，付出 35 元， 求应找回多少元。先求出李叔叔买 8 听可口可乐所需要 的总钱数，也就是求 8 个 4 相加的和是多少，列式为 8×4；再求应找回的钱数，35-8 听可口可乐需要的钱数 =应找回的钱数，列式为 35-8×4，计算时，先算 8×4=32， 再算 35-32=3. （2）一个面包 5 元，一袋牛奶 3 元，王芳买了一个面包，一袋牛奶，结果还剩 18 元，求她一共带了多少钱。也就是一个面包的钱数+一袋牛奶的钱数+剩下的 要点提示： 解决多个问题时，先根据每 个问题分析数量关系，再根 据数量关系找出解决各个 问题需要的已知信息。 钱=一共带的钱数，列式为 5+3+18，按照从左往右的顺序进行计算，求出和是 26. （3）根据题目体操其它用两步计算的数学问题，答案不唯一。如：用买 4 袋牛 奶的钱可以买几听可口可乐。 解答： （1）35-8×4=3（元）答：应找回 3 元。 （2）5+3+18=26（元）答：她一共带了 26 元钱。 （3）答案不唯一。 用买 4 袋牛奶的钱可以买几听可口可乐？ 3×4÷4=3（听）答：用买 4 袋牛奶的钱可以买 3 听可口可乐。 【例 3】在下面的四幅图的括号中写上小朋友的名字。 解析： 小朋友们站在不同位置观察杯子，他们看到的杯子是 不一样的。小华看到的是杯子把儿朝向自己，小明看到 的是杯子把儿朝向左面，小亮看不到杯子把儿，小杰 看到的是杯子把儿朝右。 解答： 【例 4】把 211、212、213、214 这四个数填入框中，使等式成立。 □+□-□=□ 要点提示： 解决观察图形的实际问题时， 一定要从侧面、正面、上面三 个角度看到的图形去考虑。 解析： 根据加减法的意义和 数的特点考虑，可以把原式变为 □+□=□+□。这 4 个数是 4 个连续的自然数，相邻两个 自然数相差 1，所以首尾两数的和等于中间两数的和，把 这 4 个数写成两个和相等的算式，然后再变回原式就可以了。 解答： 211+214-212=213 或 211+214-213=212 或 212+213-211=214 或 212+213-214=211. 【例 5】欢乐剧场的观众席分 A、B、C 三个区，A 区有 244 个座位，B 区有 228 个座 位，C 区比 A、B 两区的总和少 122 个座位，欢乐剧场一共能容纳多少名观 众？ 解析： 已知欢乐剧场的观众席分 A、B、C 三个区，A 区有 244 个座位，B 区有 228 个座位，C 区比 A、B 两区的总和少 122 个座位，欢乐剧场一共能容纳多少名观众。先求出 C 区的观众总数量，A 区观众数量+B 区观众数量-122= C 区观众数量，列式为 244+228-122，求出得数是 350；再求出一共能容纳的观 众总数量，也就是把这三个区的观众数量合在一起，选择连加列式计算，列式为 244+228+350，求出和是 822. 解答： 244+228-122 244+228+350=822 =472-122 =472+350 =350（名） =822（名） 答：欢乐剧场一共能容纳 822 名观众. 【例 6】动脑筋。 已知△+○=□，△+○+□=60，那么□=（ ）。 解析： 已知△+○=□，△+○+□=60，求□=（ ）。我们可以 把第一个算式△+○=□，代入第二个算式△+○+□=60 中， 要点提示： 根据被减数-减数=差，可以 知道被减数=减数+差。 要点提示： 求一共的观众总数，就是把 三个区的观众数量合在一 起，求和。 要点提示： 把第一个算式等量代换到 第二个算式，是解决此类问 题的关键。 也就是□+□=60，故□=30。 解答： 30. 【例 7】要把一个长 9 厘米，宽 7 厘米的长方形剪成一个最大的正方形，剪去的 长方形的周长是多少厘米？ 解析： 要把一个长 9 厘米，宽 7 厘米的长方形剪成一个最大 的正方形，求剪去的长方形的周长是多少厘米。先求出 剪成的最大正方形的边长，也就是长方形的宽，是 7 厘米； 再求出剪去的长方形的长和宽，长是原来长方形的长 7 厘米，宽是原来长方形的长减去剪成正方形的边长，列式为 9-7=2 厘米；最后 求出剪去长方形的周长，（7+2）×2. 解答： （9-7+7）×2=18（厘米） 答：剪去的长方形的周长是 18 厘米. 【例 8】请把 2、4、5、0 这四个数填入□里，要使积最大，应该怎样填？ □□□×□ 解析： 要使积最大，最大数 5 应是一位数，第二大数 4 应该 是三位数的首位，2 放在三位数的十位上，0 放在三位数 的个位上，这时所得的积最大。 解答： 420×5. 【例 9】一列火车 6 时从甲站开出，15 时到达乙站。这列火车平均每小时行 150 要点提示： 把一个长方形剪成最大的 正方形，此时正方形的边长 是长方形的宽。 要点提示： 认真审题，仔细思考是解决此类问 题的关键。 千米，甲、乙两站相距多少千米？ 解析： 根据题意可以知道：一列火车 6 时从甲站开出，15 时 到达乙站。这列火车平均每小时行 150 千米，求甲、乙 两站相距的千米数。先求出火车行驶的时间=15 时-6 时 =9 小时；再求出甲、乙两站相距的千米数=150×9. 解答： 150×（15-6） =150×9 =1350（千米）答：甲、乙两站相距 1350 千米. 【例 10】一桶油，连桶共重 138.4 千克，连桶用去一半后，剩下的油连桶重 75.5 千克，油桶重多少千克？ 解析： 要求油桶重多少千克，需要知道油的质量，根据“用去 一半 后，剩下的油连桶重 75.5 千克”可以知道，从原来 的 138.4 千克到 75.5 千克，少了 138.4-75.5=62.9 （千克），也就是一半的油是 62.9 千克，用剩下的油连桶 的重量 75.5 千克减去一半油的重量 62.9 千克，就是油桶的重量；或者求出总共 的油重：62.9+62.9=125.8（千克），再用油连桶的总重量 138.4 减去 125.8，得 出油桶的重量。 解答： 方法一：138.4-75.5=62.9（千克） 75.5-62.9=12.6（千克） 方法二：138.4-75.5=62.9（千克） 62.9+62.9=125.8（千克） 138.4-125.8=12.6（千克） 答：油桶重 12.6 千克. 三年级上册第六单元拔高题-乘法 【例 1】竖式计算。 要点提示： 火车每小时行 150 千米×火 车经过的时间=甲、乙两站 相距的距离。 要点提示： 从不同角度思考问题并解 决是数学中常见的解题思 想。 【例 2】一只烧鹅 36 元，一箱鸡蛋 24 元，妈妈买了 2 只烧鹅和 1 箱鸡蛋，共需 要多少元？ 【例 3】学校图书室有 3 个大书架，每个书架有 5 层，每层可放 35 本书，这些 书架一共能放多少本书？ 【例 4】阳关小学 4 名老师带领 92 名学生参观科技馆，用 500 元买门票，够吗？ 三年级上册第六单元拔高题-乘法 参考答案 【例 1】竖式计算。 解析： 多位数乘一位数的竖式计算方法：一位数与多位数的 个位对齐，从个位乘起，哪一位的积满几十就要向 前一位进几，前一位乘完所得的积要加上进位数。如 计算：243×4。 243×4=972. 解答： 144 768 972 1510 1470 1821. 【例 2】一只烧鹅 36 元，一箱鸡蛋 24 元，妈妈买了 2 只烧鹅和 1 箱鸡蛋，共需 要多少元？ 解析： 要求妈妈买了 2 只烧鹅和 1 箱鸡蛋，共需要多少钱， 先求出买 2 只烧鹅需要的总钱数，2×每只烧鹅的钱数 =买 2 只烧鹅需要的总钱数，列式为 36×2；再求共 需要的总钱数，2 只烧鹅的钱数+1 箱鸡蛋的钱数= 共需要的钱数，列式为 36×2+24。 解答： 36×2+24 =72+24 =96（元）答：共需要 96 元. 要点提示： 在计算进位乘法时要注意，哪一位 满几十就要向相邻的高位进几，在 相邻高位乘完后不要忘记加进上 来的数。 要点提示： 用竖式计算多位数乘一位数时， 一位数与哪一位上的数相乘，所 得的积就写在那一位下面。 【例 3】学校图书室有 3 个大书架，每个书架有 5 层，每层可放 35 本书，这些 书架一共能放多少本书？ 解析： 先求出大书架共有几层，也就是 3 个 5 相加的和， 列式为 3×5；再求出这些书架一共能放的书的本数， 列式为 3×5×35。 解答： 3×5×35 =15×35 =525（本）答：这些书架一共能放 525 本书. 【例 4】阳关小学 4 名老师带领 92 名学生参观科技馆，用 500 元买门票，够吗？ 解析： 分别求出老师和学生买门票需要的钱数，再把两部分门票 钱数合在一起，最后再和 500 元比较，比 500 元少，则够， 否则不够。 解答： 8×4=32（元） 92×5=460（元） 32+460=492（元） 492<500 答：用 500 元买门票，够. 三年级上册第七单元拔高题-年、月、日 【例 1】用 24 时记时法表示下面的时刻。 上午 8 时（ ） 中午 12 时（ ） 下午 1 时 30 分（ ） 晚上 10 时 15 分（ ） 要点提示： 计算连乘混合运算时，按照 从左往右的顺序依次进行 计算。 要点提示： 先求出买票需要的总钱数， 再和 500 元作比较。 【例 2】用 普通记时法表示下面的时刻。 17 时（ ） 20 时( ) 9 时（ ） 11 时 20 分（ ） 21 时（ ） 7 时（ ） 0 时（ ） 15 时 45 分（ ） 【例 3】电视机厂一个季度生产电视机 600 台，平均每个月生产多少台？ 【例 4】科技馆开馆时间如下表，科技馆每天开馆多长时间？ 三年级上册第七单元拔高题-年、月、日 参考答案 【例 1】用 24 时记时法表示下面的时刻。 上午 8 时（ ） 中午 12 时（ ） 下午 1 时 30 分（ ） 晚上 10 时 15 分（ ） 解析： 用普通记时法的时刻加 12 就是 24 时记时法。如： 下午 1 时 30 分，用 24 时记时法表示是：1 时 30 分+ 12 时=13 时 30 分。 解答： 8 时 12 时 13 时 30 分 22 时 15 分. 【例 2】用 普通记时法表示下面的时刻。 17 时（ ） 20 时( ) 9 时（ ） 11 时 20 分（ ） 21 时（ ） 7 时（ ） 0 时（ ） 15 时 45 分（ ） 解析： 17 时用普通记时法表示是 17 时-12=5 时，即下午 5 时； 20 时用普通记时法表示是 20 时-12=8 时，即下午 8 时； 9 时用普通记时法是上午 9 时； 11 时 20 分用普通记时法表示是上午 11 时 20 分； 21 时用普通记时法表示是 21 时-12=9 时，即下午 9 时； 7 时用普通记时法表示是上午 7 时； 0 时用普通记时法表示晚上 12 时； 15 时 45 分用普通记时法表示是 15 时 45 分-12=3 时 45 分，即下午 3 时 45 分。 解答： 下午 5 时 下午 8 时 上午 9 时 上午 11 时 20 分 下午 9 时 上午 7 时 晚上 12 时 下午 3 时 45 分. 【例 3】电视机厂一个季度生产电视机 600 台，平均每个月生产多少台？ 解析： 求平均每个月生产的电视机的台数，列式为生产电视机 的总数量÷3 个月=平均每个月生产的电视机的台数，即 600÷3。 要点提示： 采用从 0 时到 24 时的记时 方法就是 24 时记时法。 要点提示： 用 24 时记时法的时刻减 12 就是普通记时法。 要点提示： 一个季度是由 3 个月组成 的。 解答： 600÷3=200（台） 答：平均每个月生产 200 台. 【例 4】科技馆开馆时间如下表，科技馆每天开馆多长时间？ 解析： 先分别求出科技馆上午和下午开馆时间，再求出科技馆 每天开馆时间。根据科技馆上午开馆时间=上午结束时刻 -开始开馆时刻=11：00-8：30=2 小时 30 分；科技馆下午 开馆时间=下午关馆时刻-开始开馆时刻=17：20-13：30=3 小时 50 分；再把上午 开馆时间加上下午开馆时间就等于科技馆每天开馆时间，列式为 2 小时 30 分+3 小时 50 分。 解答： 11：00-8：30=2 小时 30 分 17：20-13：30=3 小时 50 分 2 小时 30 分+3 小时 50 分=6 小时 20 分 答：科技馆每天开馆 6 小时 20 分. 要点提示： 计算经过的时间时，可以用 结束时刻减去开始时刻。