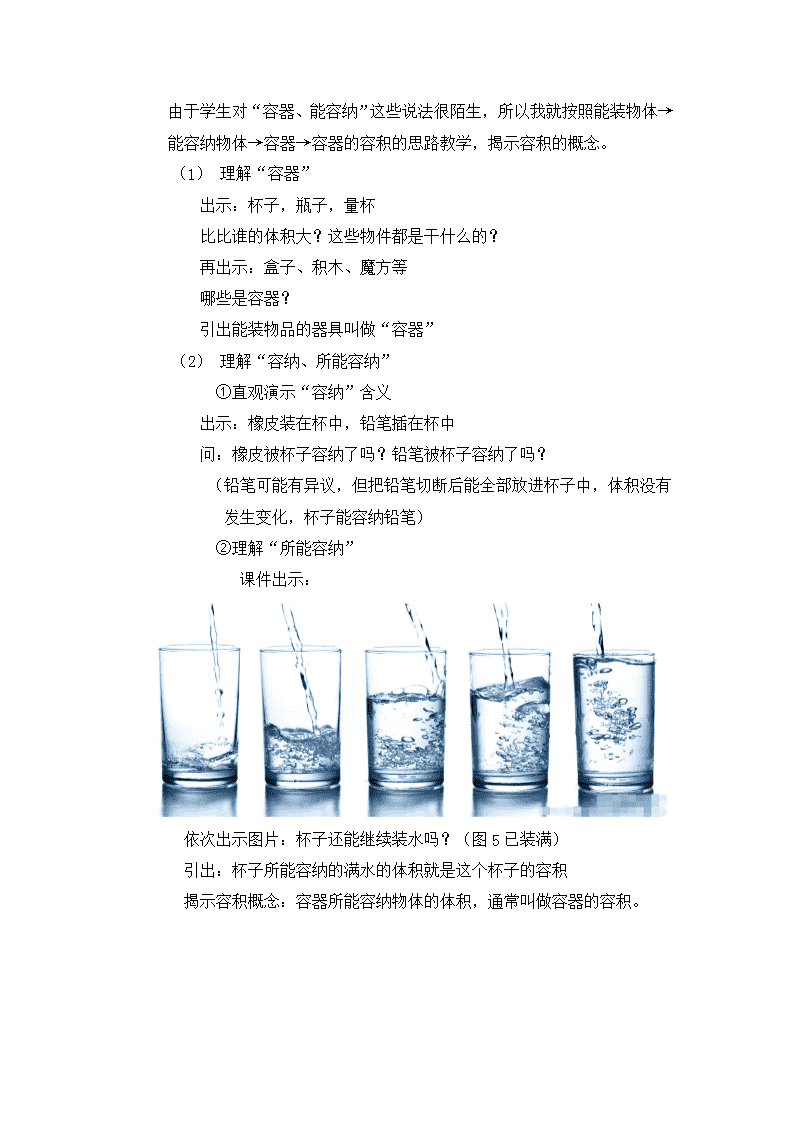五年级下册数学说课教案 4 体积与容积 沪教版 5页

数学《体积与容积》说课稿 一、说教材 我说课的内容是小学数学第十册第四单元的内容——《体积与容积》，在此 之前学生已经掌握了长方体、正方体的特征即体积计算，形成了一定的空间观念。 本课的学习，目的是使学生初步理解体积与容积之间的联系的，进一步培养学生 的空间观念。 根据学生的认知能力，教材的要求我确定了以下教学目标： 1、进一步认识容积和容积单位升、毫升。 2、认识容积单位和体积单位间的关系，并能进行换算。 3、初步体会容积与体积的区别和联系。 4、通过观察、分析、比较、操作等实践活动，培养空间观念。 教学重点：认识并感知容积的实际含义 教学难点：体积与容积的联系。 教具准备：课件、杯子、瓶子、量杯、红薯、土豆等。 二、说教法 本课属于概念教学，为了使抽象概念具体化，我主要采用直观试验的方法， 辅以“情境探究”法、“观察法”、“演示法”、“比较法”等，进行教学。 在学生的学法选择上，我采用了让学生动手操作，独立探究，合作交流的学 习模式。让学生在充分体验的基础上理解概念，这也是符合学生的认知发展规律 的。 我主要设计了以下教学流程: 第一环节：设疑体积与容积的联系 以阿基米德测皇冠故事引入，他引用了什么原理，体积与容积究竟有什么联 系，以此来激发孩子的学习兴趣。 第二环节：容积概念的学习 1、理解“容器、容纳、容积”的含义 由于学生对“容器、能容纳”这些说法很陌生，所以我就按照能装物体→ 能容纳物体→容器→容器的容积的思路教学，揭示容积的概念。 （1） 理解“容器” 出示：杯子，瓶子，量杯 比比谁的体积大？这些物件都是干什么的？ 再出示：盒子、积木、魔方等 哪些是容器？ 引出能装物品的器具叫做“容器” （2） 理解“容纳、所能容纳” ①直观演示“容纳”含义 出示：橡皮装在杯中，铅笔插在杯中 问：橡皮被杯子容纳了吗？铅笔被杯子容纳了吗？ （铅笔可能有异议，但把铅笔切断后能全部放进杯子中，体积没有 发生变化，杯子能容纳铅笔） ②理解“所能容纳” 课件出示： 依次出示图片：杯子还能继续装水吗？（图 5 已装满） 引出：杯子所能容纳的满水的体积就是这个杯子的容积 揭示容积概念：容器所能容纳物体的体积，通常叫做容器的容积。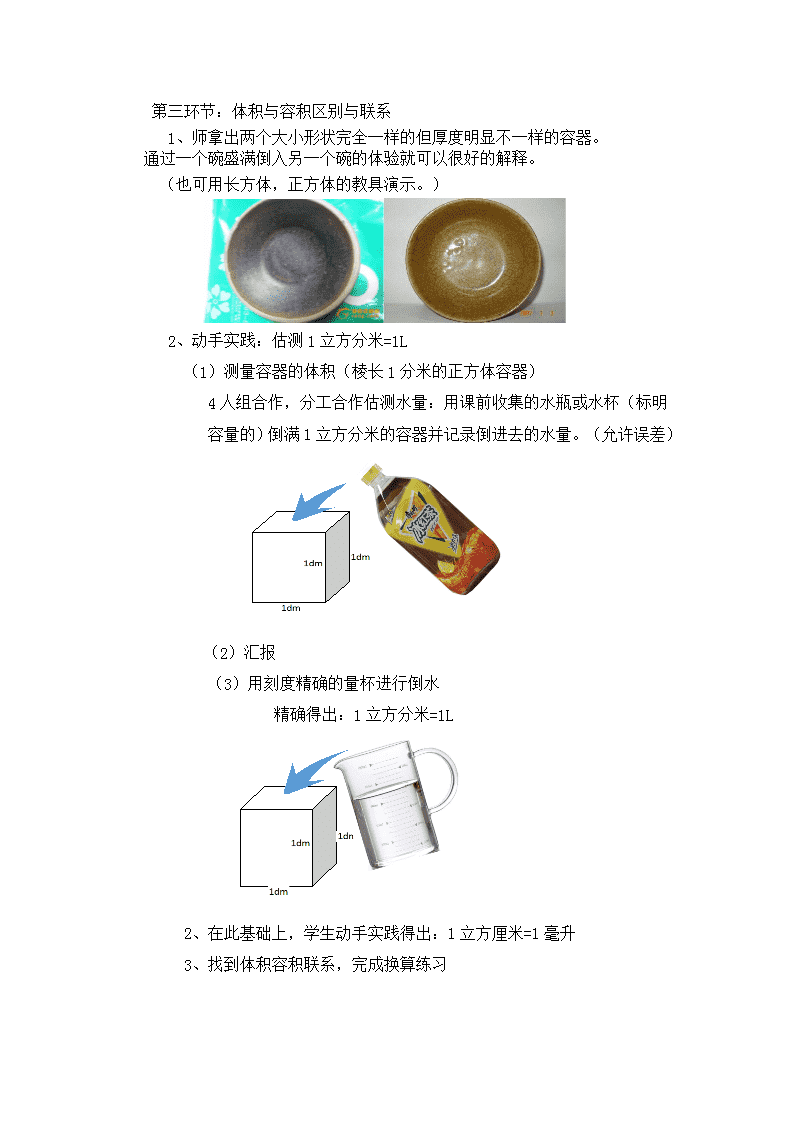 第三环节：体积与容积区别与联系 1、师拿出两个大小形状完全一样的但厚度明显不一样的容器。 通过一个碗盛满倒入另一个碗的体验就可以很好的解释。 （也可用长方体，正方体的教具演示。） 2、动手实践：估测 1 立方分米=1L （1）测量容器的体积（棱长 1 分米的正方体容器） 4 人组合作，分工合作估测水量：用课前收集的水瓶或水杯（标明 容量的）倒满 1 立方分米的容器并记录倒进去的水量。（允许误差） （2）汇报 （3）用刻度精确的量杯进行倒水 精确得出：1 立方分米=1L 2、在此基础上，学生动手实践得出：1 立方厘米=1 毫升 3、找到体积容积联系，完成换算练习 第四环节：体积与容积的应用 活动：比较大小相近的不规则物体（土豆和红薯）的体积， 4 人组操作实践 设计方案(“联系引入的阿基米德的方法) （用两个一样大小的容器，装一样多的水，分别放入土豆和红薯， 再比较水的上升部分） （1）、小组讨论设计方案（需要精确的量杯） （2）、一起设计表格，你觉得需要记录什么信息？ （3）、动手操作，比较出土豆、红薯的体积大小 第五环节：借助“不为五斗米折腰”的成语介绍认识古代的“升”。 “斗”是盛粮食的器具，酒器。 中国古代计量方法极为精确，且为十进位制。即：一斗为十升，每升 约重 1．5 公斤；一升为十合，每合重 150 克；一合为十勺，每勺重 15 克； 一勺为十抄，每抄重 1．5 克；一抄为十作，每作重 0．15 克；一作为十厘， 仅重 0．015 克（约一粒米） 学生在“做数学”的过程中，充分理解比较抽象的容积概念，充分发挥学 生的自主探索的能力和创新精神。实验活动能使学生始终处于积极投入状态， 从而高效地参与学习的全过程 这节课，我力求把抽象，枯燥的概念让学生学得生动、丰满，使学生在亲 身体验与感受中，把握概念的本质特征。 【板书设计】 体积与容积 1 立方厘米=1 毫升 1 立方分米=1 升 大 小 容器 容纳 体积 容积 空间物体