5年级数学教案第6讲：组合图形面积计算 7页

辅导教案 学员姓名： 学科教师： 年 级： 辅导科目： 授课日期 ××年××月××日 时 间 A / B / C / D / E / F 段 主 题 教学内容 1．复习组合图形的面积求法。 2．锻炼图形的割补能力，提高解决未知问题的能力。 上节课我们学习了一些基本图形面积的求解方法，（教师可以简单提问一下梯形面积的面积公式，平行四边形 面积公式等等）那么对于不规则图形怎么求解呢？我们来看看上节课的预习作业。 右图是一个不规则图形，如何计算它的面积？ 根据学生的完成情况，如果都不会做教师可以把一张纸拿出来，然后填上数据，并剪成图中的样子，看看学 生想到了什么，目的是引导学生用割或补的方法去思考。下图给出了 4 种常见的割补法 基本概念： 对于不规则图形的面积，一般采取“割”、“补”的方式来求解： 1．“割”：将不规则图形分割成若干块规则图形，分别求出面积后相加； 2．“补”：在不规则图形之外添上部分规则图形，拼成一个大的规则图形，从而求解。 这里可以让学生思考一下我们所谓的规则图形是什么？然后让学生明白目前的规则图形就是我们学过的能求 面积的图形，当然后面我们还会学到圆的面积求解方法，它也是规则图形。 建议例题算法由老师讲解，练习由学生轮流回答 例 1. 已知每个小方格的面积均为 1 平方厘米，求出下列各个图形的面积： 按行从左到右答案：7.5 平方厘米； 6 平方厘米；21 平方厘米；6 平方厘米； 14 平方厘米 讲解时要让学生明确何时应该采用割补法，不规则图形一定要割补，对于规则图形但是底边没有在横纵网格 上，也需要割补，割补的目的就是让规则图形的底边落在横纵网格上，例如第二行第一个三角形。如果学生 分割不好的话可以让学生学会最简单的补长方形的方法，然后减去多余的三角形就可以了。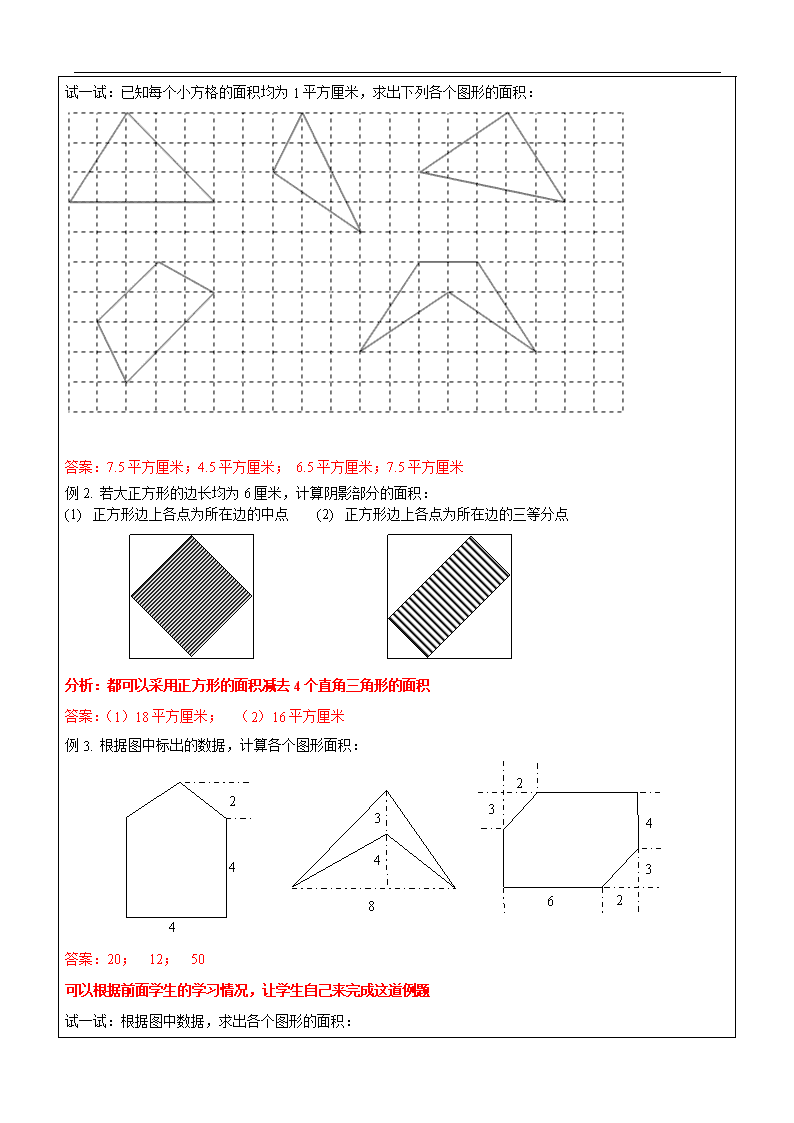 试一试：已知每个小方格的面积均为 1 平方厘米，求出下列各个图形的面积： 答案：7.5 平方厘米；4.5 平方厘米； 6.5 平方厘米；7.5 平方厘米 例 2. 若大正方形的边长均为 6 厘米，计算阴影部分的面积： (1) 正方形边上各点为所在边的中点 (2) 正方形边上各点为所在边的三等分点 分析：都可以采用正方形的面积减去 4 个直角三角形的面积 答案：（1）18 平方厘米； （2）16 平方厘米 例 3. 根据图中标出的数据，计算各个图形面积： 答案：20； 12； 50 可以根据前面学生的学习情况，让学生自己来完成这道例题 试一试：根据图中数据，求出各个图形的面积： 4 4 2 8 3 4 6 2 3 4 3 2 答案：20； 42 例 4. 计算下列图形中阴影部分的面积。 (1) (2) (3) 答案：（1）18 （可以补成长方形减去三个三角形） （2）14 （可以用两个正方形减去两个三角形或两个梯形） （3）6 （可以分割成两个三角形或者补成大长方形，减去三个三角形） 试一试：根据图中数据，求出阴影部分的面积： 答案：12， 9.5， 3.5 由学生独立完成，然后交换批改，进行讲解评比 1．已知每个小方格的面积均为 1 平方厘米，求出下列各个图形的面积： 4 4 7 15 8 1 6 4 1 326 4 53 53 1 1 1 答案：6， 8.5， 8， 2．根据所标出的数据，计算下列图形的面积： 答案：48，（分割成长方形和三角形） 14（两个长方形面积减去中间小正方形面积） 3．根据图中数据，求出阴影部分的面积： 答案：17，（两个正方形减去两个三角形或分割成两个三角形）， 5（可以填补算 5 个正方形面积，也可以补 成正方形减去四个三角形） 附加题：如图所示，在这样一个直角三角形中放入一个尽可能大的正方形，它的边长是多少？ 4 6 4 4 8 10 5 1 1 53 1 答案：分割成两个三角形，设正方形边长为 a，通过两个三角形面积和等于大三角形列方程解出 a=2.4 本节课主要知识：不规则图形的求解方法，割补法的目的是什么，应该如何操作。 1．已知每个小方格的面积均为 1 平方厘米，求出下列各个图形的面积： 答案：10， 12， 21 2．根据所标出的数据，计算下列图形或阴影部分的面积： 4 6 4 2 10 15 1 1 8 2 答案：48， 126 生活中我们会见到很多长方体正方体的图形，请同学们试着举例说明。然后说说它有几个面有多少条棱多少 个定点？