五年级下册数学课件-6 总复习：图形与几何（平面图形的周长和面积） ▏沪教版 (共21张PPT) 21页

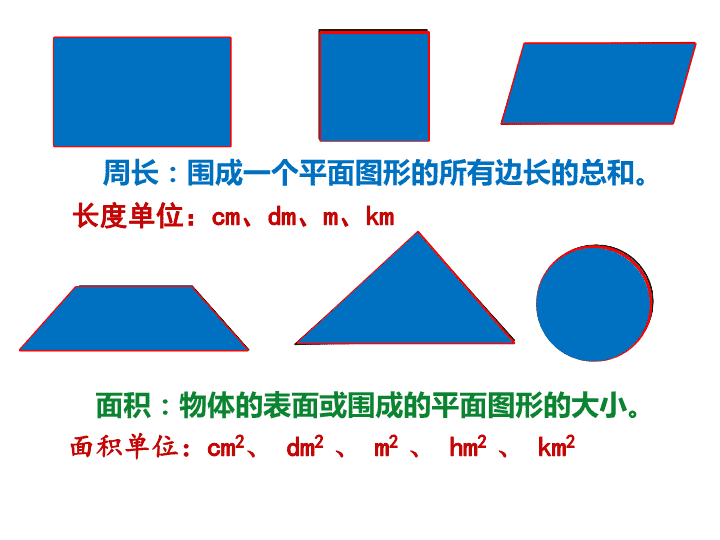
平面图形周长和面积总复习 你学 过了哪些关于 平面图形 周长和面积 的 知识？ 周长：围成一个平面图形的所有边长的总和。 长度单位 ： cm 、 dm 、 m 、 km 面积：物体的表面或围成的平面图形的大小。 面积单位 ： cm 2 、 dm 2 、 m 2 、 hm 2 、 km 2 每组中两个图形的周长相等吗？面积呢？ C= π d C=(a+b)×2 C=4a C=2 π r 周长 面积 S=ab S=a 2 S=ah S =( a+b)h÷2 S=ah÷2 S= π r 2 知其然 知其所以然 … 追根 溯源 小组合作要求： 1 、每人至少选择 1 ~ 2 个图形，在小组时说说它的面积是怎样推导的。 2 、思考交流：在推导过程中用了哪些的方法？有什么共同的思想支撑 ？ 通过 摆一摆，数一数。 长方形的面积 = 长 Χ 宽 S=ab 转化 正方形的面积 = 边长 Χ 边长 S=a 2 长方形和正方形的面积推导 底 高 长方形的面积 平行四边形的面积 底 高 = Χ 转化 = Χ 平行四边形的面积推导 S=ah 长 宽 底 高 三角形面积推导过程： 三角形的面积推导 底 高 平行四边形的面积 三角形的面积 高 = Χ 转化 底 高 底 = Χ ÷2 S=ah÷2 三角形面积推导过程： 梯形的面积推导 底 平行四边形的面积 梯形的面积 高 = Χ 转化 （上底 + 下底） 高 底 = Χ ÷2 S=(a+b)h÷2 高 下底 上底 圆面积推导 …… 长方形的面积 圆的面积 r r = Χ 转化 = Χ S= r 2 长 宽 长 = r 宽 = r 圆面积推导 梯形上底是 4 厘米，下底是 10 厘米，高是 2 厘米。 （每个方格是边长 1 厘米的正方形） （ 1 ）它的面积是多少？ （ 2 ）如果把这个梯形上底 增加 3 厘米 ，下底 减少 3 厘米 ， 得到的图形面积会是多少？你发现了什么？ （ 3 ）如果把这个梯形上底 减少 4 厘米 ，下底 增加 4 厘米 ， 得到的图形面积会是多少？你发现了什么？ 梯形上底是 4 厘米，下底是 10 厘米，高是 2 厘米。 （每个方格是边长 1 厘米的正方形） （ 2 ）如果把这个梯形上底 增加 3 厘米 ，下底 减少 3 厘米 ， 得到的图形面积会是多少？你发现了什么？ 梯形上底是 4 厘米，下底是 10 厘米，高是 2 厘米。 （每个方格是边长 1 厘米的正方形） （ 2 ）如果把这个梯形上底 增加 3 厘米 ，下底 减少 3 厘米 ， 得到的图形面积会是多少？你发现了什么？ 梯形上底是 4 厘米，下底是 10 厘米，高是 2 厘米。 （每个方格是边长 1 厘米的正方形） （ 3 ）如果把这个梯形上底 减少 4 厘米 ，下底 增加 4 厘米 ， 得到的图形面积会是多少？你发现了什么？ Thanks!