五年级数学上册第四单元多边形的面积练习五教学课件北师大版 13页

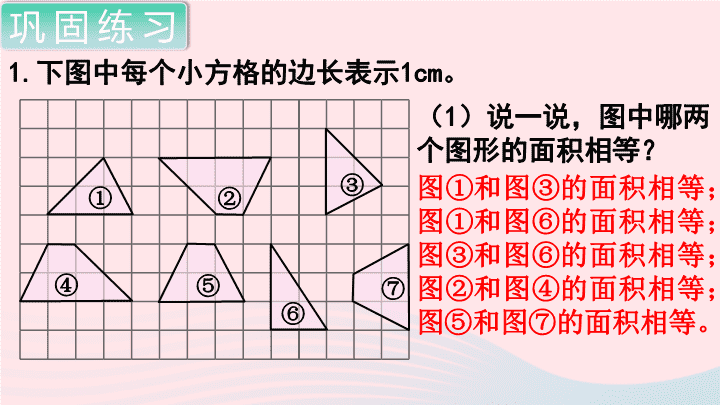
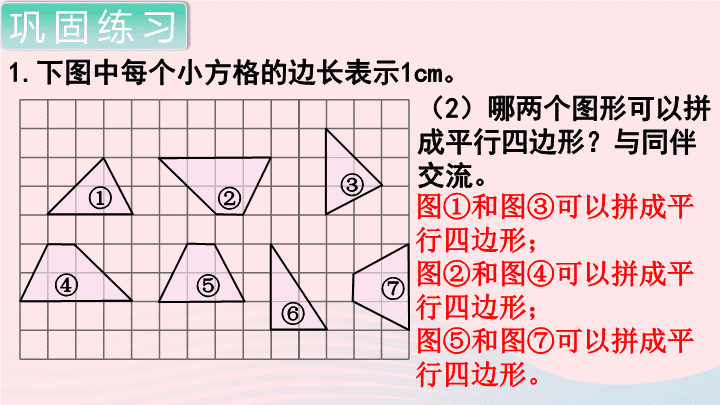
练 习 五 多边形的面积 四 1.下图中每个小方格的边长表示 1cm。 巩固练习 ① ② ③ ⑤ ⑦ ⑥ ④ （1）说一说，图中哪两个图形的面积相等？ 图①和图③的面积相等； 图①和图 ⑥ 的面积相等；图③和图⑥的面积相等；图 ② 和图 ④ 的面积相等；图 ⑤ 和图 ⑦ 的面积相等。 1.下图中每个小方格的边长表示 1cm。 巩固练习 ① ② ③ ⑤ ⑦ ⑥ ④ （ 2 ）哪两个图形可以拼成平行四边形？与同伴交流。 图①和图③可以拼成平 行四边形； 图②和图④可以拼成平 行四边形； 图⑤和图⑦可以拼成平 行四边形。 2. 量出相关数据，计算并比较下列图形的面积，你有什么发现？ 巩固练习 3cm 2cm 3cm 2cm 3cm 2cm 3cm 1cm 2cm S=3 × 2 =6cm² S=3 × 2 =6cm² S=3 × 2 ÷ 2 =3cm² S= （ 3+1 ）× 2 ÷ 2 =4cm² 3. 涂色的三角形面积是平行四边形面积的一半吗？说一说你的理由。 巩固练习 涂色的三角形和平行四边形等底等高，因此涂色的三角形面积是平行四边形面积的一半。 4. 下面的图形是由哪些基本图形（长方形、平行四边形、三角形或梯形）组成的？请你动手画一画，并与同伴交 流。 有多种组合方式，合理即可。 巩固练习 5. 计算下面图形的面积。 巩固练习 13m 5m 13 × 5=65 （ m² ） 16m 10dm 12m 4m 6dm （ 4+12 ）× 16 ÷ 2=128 （ m² ） 10 × 6 ÷ 2=30 （ dm² ） 6. 如图，一个直角三角形的面积是 90cm² ，一条直角边长 7.2cm ，另一条直角边长是多少？ 巩固练习 7.2m 90 × 2 ÷ 7.2=25 （ m ） 答：另一条直角边长 25 厘米。 7. （ 1 ）如图，梯形的面积是多少？ （ 4+10 ）× 5 ÷ 2=35 （ cm² ） （ 4+1+10 － 1 ）× 5 ÷ 2=35 （ cm² ） 得到的新梯形和原梯形的面积相等。 巩固练习 5cm 4cm 10cm （ 2 ）如果把这个梯形的上底增加 1cm 、下底减少 1cm ，得到的新梯形和原梯形的面积之间有什么关系？ 7. （ 3 ）如果梯形的上底增加 2cm ，下底减少 2cm 呢？ （ 4+2+10 － 2 ）× 5 ÷ 2=35 （ cm² ） 得到的新梯形和原梯形的面积相等。 如果梯形的上底（或下底）增加 n cm ，下底（或上底）减少 n cm ，那么得到的新梯形和原梯形的面积相等。（ n 的取值范围在条件允许的范围内） 巩固练习 5cm 4cm 10cm （ 4 ）你发现了什么？尝试说明理由。 8. （ 1 ）如图，平行四边形的面积是多少？ 4 × 4=16 （ cm² ） （ 4+1 ）×（ 4 － 1 ） =15 （ cm² ） 得到的新平行四边形比原平行四边形的面积少 1cm² 。 巩固练习 4cm 4cm （ 2 ）如果平行四边形的高增加 1cm 、底减少 1cm ，得到的新平行四边形和原平行四边形的面积之间有什么关系？ 8. （ 3 ）如果平行四边形的高增加 2cm ，底减 少 2cm 呢？ （ 4+2 ）×（ 4 － 2 ） =12 （ cm² ） 得到的新平行四边形比原平行四边形的面积少 4cm² 。 巩固练习 4cm 4cm （ 4 ）你发现了什么？举例验证你的发现。 如果平行四边形的底减少 n cm ，高增加 n cm ，那么得到的新平行四边形比原平行四边形的面积少 n² cm² 。 （ n 的取值范围在条件允许范围之内） 9. 实践活动。 巩固练习 在我们身边有许多物体的表面是平行四边形、三角形或梯形，请你先估计它们的面积，再测出有关的数据，计算它们的面积，并将二者进行比较。 物体 物体表面的形状 面积估计值 测量数据 面积计算值 可选择红领巾、流动红旗等进行估算、测量和计算。