北师大版六年级上册数学期末模拟冲刺卷4 21页

北师大版六年级上册数学期末模拟冲刺卷 4 考试时间：90 分钟；满分：100 分 学校:___________姓名：___________班级：___________考号：___________[来源:学 ZXXK] 题号 一[来源: ZXXK] 二[XXK] 三 四[来源:学#科#网] 五 六 总分 得分 注意事项：1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上 一．填空题（共 11小题, 每空 1 分，共 20 分） 1．36  284 : 5 ( )    %  折[来源:学科网 ZXXK] 2． 6 : 8的比值是 ；把 1.4米：70厘米化成最简单的整数比是 ． 3．从甲地到乙地，小华用了 5小时，小红用了 3小时．小华和小红所用的时间的比是 ，他们的速度比 是 ． 4．月球探测是一项非常复杂并具有高风险的工程，截至目前包括“嫦娥三号”在内，世界上共进行了 130 次月球探测活动，其中成功 67次，成功率是 %． 5．李叔叔把 5000元按一年期整存整取存在银行，年利率 3.87%，利息税是 5%，到期后可得税后利息 元． 6．永辉超市周年店庆搞活动、一件毛衣标价 500元，普通顾客可八折购买，会员凭会员卡可七五折购买．买 一件这样的毛衣，普通顾客要花 元，会员要花 元，会员比普通顾客节省了 元．[来源:学科网 ZXXK] 7．一桶蜂蜜 4千克，第一次拿出蜂蜜的 1 5 ，第二次倒出 1 5 千克，桶内还剩蜂蜜 千克． 8．小马虎在计算 4 ( 3  □ 4) 5  时错看成了 4 3 □ 4 5  ，这样得到的结果与正确答案相差 ． 9．已知一个半圆形的直径是 8厘米，这个半圆形的周长是 厘米． 10．如图，把圆分成若干等份，剪拼成一个近似的长方形，已知长方形的宽为5cm， 则长是 cm，长方形的面积是 2cm ． 11．某班原有男生 30人，男生和女生的人数比是 5 : 4，则女生有 人．现在转进女生 1人，那么女生与 全班人数的比是 ． 二．判断题（共 5小题，每小题 1 分，共 5 分）[来源:学科网] 12．把一张圆形纸片从不同方向折叠，折痕都经过圆心． （ ） 13．在一个长为 4分米、宽为 3分米的长方形内可以画一个直径为 4分米的圆．（ ） 14．如果男生比女生多 1 4 ，那么女生就比男生少 1 4 ． （ ） 15．大牛和小牛头数的比是 3 : 5，表示大牛比小牛少 2 5 ． （ ） 16．把 0.12 :1的后项化成 100，要使比值不变，则这个比为120 :100 （ ） 三．选择题（共 5小题，每小题 2 分，共 10 分） 17．如图图形中，从右面看的形状是 的有 ( ) A．只有① B．② C．①和③ 18．一件商品原价 200元，涨价 1 4 后再降价 1 4 ，现价 ( )原价． A．高于 B．低于 C．等于 19．长方形的周长 40cm，长与宽的比是 5 : 3，面积是 ( ) A． 2375cm B． 215cm C． 293.75cm D． 245cm 20．某商店有 500台电视机，第一天卖掉了 20%，第二天又进了一部分电视机，进的台数是第一天剩余台 数的 20%，现在电视机有 ( )台． A．540 B．520 C．500 D．480 21．一个圆形钟面，分针长 6厘米，经过 60分钟，分针针尖走过了 ( )厘米． A．37.68 B．21.4 C．28.26 D．25.12 四．计算题（共 4小题，共 32 分） 22．直接写得数．（共 10 小题，每小题 0.5 分，共 5 分） 3.6 4  1 1 6 2   215 3   1 25% 4   3 3 7   25% 4  324 4   3 9 8 8   2 2 0 3 3    [来源:Z。xx。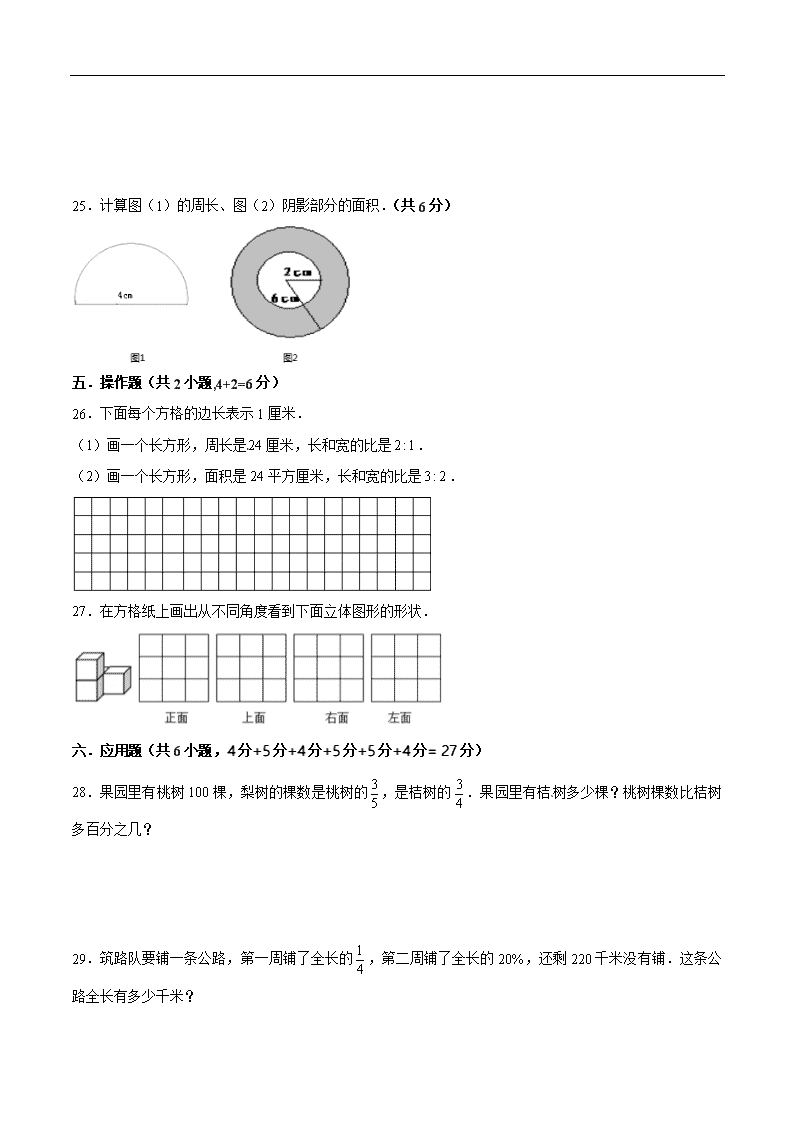k.Com] 1 1 1 1 3 4 3 4     23．怎样简便就怎样算．（每小题 3分，共 12分） （1） 3 3 4[4 ( )] 4 8 29    （2） 43.5 6.5 0.8 5    （3） 5 1 12 4 17 4 17    （4） 4 1 7 7( ) 5 4 3 10    24．解方程．（每小题 3分，共 9分） 2 50% 300 3 x x  60% 35% 125x x  4.1 30% 2x  25．计算图（1）的周长、图（2）阴影部分的面积．（共 6分） 五．操作题（共 2小题,4+2=6分） 26．下面每个方格的边长表示 1厘米． （1）画一个长方形，周长是24厘米，长和宽的比是 2 :1． （2）画一个长方形，面积是 24平方厘米，长和宽的比是 3 : 2． 27．在方格纸上画出从不同角度看到下面立体图形的形状． 六．应用题（共 6小题，4 分+5 分+4 分+5 分+5 分+4 分= 27 分） 28．果园里有桃树 100棵，梨树的棵数是桃树的 3 5 ，是桔树的 3 4 ．果园里有桔树多少棵？桃树棵数比桔树 多百分之几？ 29．筑路队要铺一条公路，第一周铺了全长的 1 4 ，第二周铺了全长的 20%，还剩 220千米没有铺．这条公 路全长有多少千米？ 30．某天六年级一班出勤的人数是 38人，有 2人缺勤．该班这天的出勤率是多少？ 31．一个圆形花坛的直径是 6米，现在要扩建花坛，把它的半径增加 1米． （1）花坛的面积比原来增加了多少平方米？ （2）花坛的周长比原来增加多少米？ 32．用一根长 72分米的铁丝做一个长方体框架，使它的长、宽、高的比是 4 :3 : 2．如果在这个长方体框架 外面糊一层纸，至少需要多少平方分米的纸？ 33．六年 ( 1 )班全体同学投票选班长，毎位同学投且只能投一票，得票数最高者当选．下面是全部候选人 得票情况統汁图． （1）当选班长的同学姓名是 ． （2）王倩得票数占总票数的 %． （3）如果张力得 4票，那么吴佳得多少票？ 参考答案与试题解析 一．填空题（共 11小题, 每空 1 分，共 20 分） 1．36  45 284 : 5 ( )    %  折 【分析】根据比与除法的关系 4 : 5 4 5  ，再根据商不变的性质被除数、除数都乘 9 就是 36 45 ；根据比 与分数的关系 44 : 5 5  ，再根据分数的基本性质分子、分母都乘 7就是 28 35 ； 4 5 0.8  ，把 0.8的小数点向 右移动两位添上百分号就是80% ；根据折扣的意义80% 就是八折． 【解答】解： 2836 45 4 : 5 80% 35     八折． 故答案为：45，35，80，八． 【点评】此题主要是考查除法、分数、百分数、比、折扣之间的关系及转化．利用它们之间的关系和性质 进行转化即可． 2． 6 : 8的比值是 0.75 ；把 1.4米：70厘米化成最简单的整数比是 ． 【分析】（1）用比的前项除以后项即可； （2）先把比的两项的单位统一，再根据比的基本性质作答，即比的前项和后项同时乘或除以一个数 (0除外） 比值不变． 【解答】解：（1） 6 : 8 6 8  0.75 ； （2）1.4米：70厘米 140 厘米：70厘米 (140 70) : (70 70)   2 :1 ； 故答案为：0.75， 2 :1． 【点评】此题主要考查了化简比和求比值的方法，另外还要注意化简比的结果是一个比，它的前项和后项 都是整数，并且是互质数；而求比值的结果是一个商，可以是整数，小数或分数． 3．从甲地到乙地，小华用了 5小时，小红用了 3小时．小华和小红所用的时间的比是 5 : 3 ，他们的速 度比是 ． 【分析】根据题意，求出小华和小红所用时间的比；把从甲地到乙地的路程看作单位“1”，根据“路程 时 间 速度”分别求出小华和小红的速度，进而根据题意求比即可． 【解答】解： 5 : 3 (1 5) : (1 3)  1 1: 5 3  3:5 ； 答：小华和小红所用的时间的比是 5 : 3，他们的速度比是 3 : 5． 故答案为： 5 : 3，3 : 5． 【点评】解答此题用到的知识点：（1）比的意义；（2）路程、时间和速度三者之间的关系． 4．月球探测是一项非常复杂并具有高风险的工程，截至目前包括“嫦娥三号”在内，世界上共进行了 130 次月球探测活动，其中成功 67次，成功率是 51.5 %． 【分析】成功率是成功次数占总次数的百分之几，计算方法为： 100%  成功次数 总次数 成活率，由此列式解答 即可． 【解答】解： 67 100% 51.5% 130   答：成功率是 51.5%； 故答案为：51.5． 【点评】此题属于百分率问题，计算的结果最大值为100%，都是用一部分数量（或全部数量）除以全部数 量乘以百分之百． 5．李叔叔把 5000 元按一年期整存整取存在银行，年利率 3.87% ，利息税是 5% ，到期后可得税后利息 183.825 元． 【分析】本题中，本金是 5000元，利率是 3.87%，时间是 1年，利息按 5%纳税，求税后利息，根据关系 式：利息 本金利率时间 (1 5%)  ，解决问题． 【解答】解： 5000 3.87% 1 (1 5%)    193.5 0.95  183.825 （元 ) 答：到期时可得税后利息 183.825元． 故答案为：183.825． 【点评】此题属于利息问题，考查了关系式：利息 本金利率时间 (1 5%)  ，代入数据，解决问题． 6．永辉超市周年店庆搞活动、一件毛衣标价 500元，普通顾客可八折购买，会员凭会员卡可七五折购买．买 一件这样的毛衣，普通顾客要花 400 元，会员要花 元，会员比普通顾客节省了 元． 【分析】根据题意可知，把标价看作单位“1”，则：普通顾客所需钱数 标价 80% ，会员所需钱数标价 75% ．把数代入计算：500 80% 400  （元 )，500 75% 375  （元 )，然后求其差：400 375 25  （元 )．即 可求解． 【解答】解：八折 80% 七五折 75% 500 80% 400  （元 ) 500 75% 375  （元 ) 400 375 25  （元 ) 答：买一件这样的毛衣，普通顾客要花 400元，会员要花 375元，会员比普通顾客节省了 25元． 故答案为：400；375；25． 【点评】本题主要考查百分数的应用，关键找到单位“1”，利用关系式做题． 7．一桶蜂蜜 4千克，第一次拿出蜂蜜的 1 5 ，第二次倒出 1 5 千克，桶内还剩蜂蜜 3 千克． 【分析】先把这桶蜂蜜的总量看成单位“1”，第一次拿出蜂蜜的 1 5 ，用总量乘 1 5 即可求出第一次拿出的质量， 再用总质量减去两次拿出的质量，就是最后还剩下蜂蜜的质量． 【解答】解： 1 44 5 5   （千克） 4 14 ( ) 5 5   4 1  3 （千克） 答：桶内还剩蜂蜜 3千克． 故答案为：3． 【点评】此题重在区分分数在具体的题目中的区别：在具体的题目中，带单位是一个具体的数，不带单位 是把某一个数量看单位“1”，是它的几分之几． 8．小马虎在计算 4 ( 3  □ 4) 5  时错看成了 4 3 □ 4 5  ，这样得到的结果与正确答案相差 4 15 ． 【分析】直接把两个算式相减，算出结果即可． 【解答】解： 4 ( 3  □ 4 4) ( 5 3   □ 4) 5  4 3  □ 4 4 4 3 5 3    □ 4 5  16 4 15 5   4 15  ； 答：计算结果与正确答案相差 4 15 ． 故答案为： 4 15 ． 【点评】此题考查了分数的四则混合运算，解决本题，也可以把□看作一个具体的数，分别求出这两个算 式的结果，然后再进一步解答． 9．已知一个半圆形的直径是 8厘米，这个半圆形的周长是 20.56 厘米． 【分析】半圆的周长等于同直径的圆的周长的一半再加 1条直径的长度，圆的直径已知，从而可以分别求 出半圆的周长． 【解答】解： 3.14 8 2 8   12.56 8  20.56 （厘米） 答：这个半圆形的周长是 20.56厘米． 故答案为：20.56． 【点评】此题主要考查圆的周长的计算方法，关键是明白：半圆的周长等于同直径的圆的周长的一半再加 1 条直径的长度． 10．如图，把圆分成若干等份，剪拼成一个近似的长方形，已知长方形的宽为 5cm，则长是 15.7 cm， 长方形的面积是 2cm ． 【分析】根据圆面积的定义和拼成的图形的特点：近似长方形的长等于圆周长的一半，宽等于圆的半径， 然后根据圆的周长公式 2C r ，长方形的面积公式 S ab 解答即可． 【解答】解： 3.14 5 15.7( )cm  23.14 5 3.14 25  278.5( )cm 答：长是15.7cm，长方形的面积是 278.5cm ． 故答案为：15.7，78.5． 【点评】本题主要考查了学生利用知识的迁移推导圆面积公式的过程． 11．某班原有男生 30人，男生和女生的人数比是 5 : 4，则女生有 24人 人．现在转进女生 1人，那么女 生与全班人数的比是 ． 【分析】设原来有女生 x人，根据“男生人数：女生人数 5 : 4 ”即可列比例解答求出原来女生人数．用原 来的女生人数加 1人就是现在的女生人数，全班人数就是原来男、女生人数之和加又转来的 1 名女生，根 据比的意义即可写出现在女生与全班人数的比． 【解答】解：设原来有女生 x人． 30 : 5 : 4x  5 30 4x   5 5 30 4 5x     24x  (24 1) : (30 24 1)   25 : 55 5 :11 答：女生有 24人人．现在转进女生 1人，那么女生与全班人数的比是 5 :11． 故答案为：24， 5 :11． 【点评】此题是考查比和比例的应用、比的意义及化简．列比例与列方程相同，就是找出含有未知数的等 式． 二．判断题（共 5小题，每小题 1 分，共 5 分） 12．把一张圆形纸片从不同方向折叠，折痕都经过圆心．  ．（判断对错） 【分析】因为圆是中心对称图形，圆的对称轴是对折后折痕所在的直线，圆有无数条对称轴，所以你无论 对折多少次，所有的折痕都一定相交于圆的中心；进而得出结论． 【解答】解：由分析知：每条对折后的折痕都是直径所在的直线，所以一张圆形纸片对折若干次，所有折 痕都相交于圆心，但题干没有说明是“对折”，所以说法错误； 故答案为：． 【点评】此题考查的是圆的基础知识的认识，应灵活运用知识． 13．在一个长为 4分米、宽为 3分米的长方形内可以画一个直径为 4分米的圆．  ．（判断对错） 【分析】在一张长是 4分米，宽 3 分米的长方形里面画最大的圆，应以长方形的宽边为圆的直径画，如果 以 4厘米为直径，则这个长方形的宽不够，据此解答即可． 【解答】解：在一张长是 4分米，宽 3分米的长方形里面画最大的圆，应以长方形的宽边为圆的直径画． 所以题干错误． 故答案为：． 【点评】此题考查在长方形中画一个最大的圆，应以宽边为直径画，进而得出结论． 14．如果男生比女生多 1 4 ，那么女生就比男生少 1 4 ．  （判断对错） 【分析】根据“男生比女生多 1 4 ，”，把女生人数看作单位“1”，则男生人数就是它的 1(1 ) 4  ，再用男女生 人数差除以男生人数，即可求出女生比男生少几分之几，再与 1 4 比较即可． 【解答】解：： 1 1(1 ) 4 4   1 5 4 4   1 5  女生就比男生少 1 5 ，而不是 1 4 ． 故答案为：． 【点评】解决此题也可以通过判断单位“1”的量来解答，前一句话的单位“1”是女生人数，后一句话的 单位“1”是男生人数，单位“1”的量不同，所以分率就不同． 15．大牛和小牛头数的比是 3 : 5，表示大牛比小牛少 2 5 ．  ．（判断对错） 【分析】假设大牛为 3头，小牛则 5头，求大牛比小牛少几分之几，先求少 (5 3) 2  头，少的头数是 5头 的几分之几，根据求一个数是另一个数的几分之几用除法计算得出，然后进行判断． 【解答】解： 2(5 3) 5 5    ， 故答案为： ． 【点评】此题属于求一个数比另一个数多（或少）几分之几的应用题，方法是：先判断出单位“1”，然后 用（大数 小数） 单位“1”的量即可得出结论． 16．把 0.12 :1的后项化成 100，要使比值不变，则这个比为 120 :100．  （判断对错） 【分析】根据比的基本性质即比的前项和后项同时乘或除以相同的数 (0除外），比值不变． 把 0.12 :1的后 项化成 100，即1 100 100  ，那么 0.12 100 12  ，进而做出判断． 【解答】解：根据比的基本性质， 把 0.12 :1的后项化成 100，即1 100 100  ， 那么 0.12 100 12  ， 故 0.12 :1 12 :100 故答案为：． 【点评】此题重点考查比的基本性质的应用． 三．选择题（共 5小题，每小题 2 分，共 10 分） 17．如图图形中，从右面看的形状是 的有 ( ) A．只有① B．② C．①和③ 【分析】观察图形可知，从右面看：图形①看到的是 2层：下层 2个正方形，上层 1个靠左边，符合题意； 图形②看到的是一列 2个正方形，不符合题意；图形③看到的是 2层：下层 2个正方形，上层 1个靠左边， 符合题意；据此即可解答问题．[来源:学科网 ZXXK] 【解答】解：根据题干分析可得，从右面看的形状是 的有图形①和③． 故选：C． 【点评】此题考查从不同方向观察物体和几何体，意在训练学生的空间想象能力、观察、分析判断能力． 18．一件商品原价 200元，涨价 1 4 后再降价 1 4 ，现价 ( )原价． A．高于 B．低于 C．等于 【分析】先把原价看作单位“1”，涨价 1 4 后的价格是原价的 11 4  ，再降价 1 4 后的价格是涨价后的 11 4  ，即 是原价的 1 1(1 ) (1 ) 4 4    ． 【解答】解： 1 1(1 ) (1 ) 4 4    1.25 0.75  93.75% 即此时价格是原价的 93.75%， 93.75% 1 ，低于原价． 故选： B． 【点评】完成本题要注意前后两个 1 4 的单位“1”是不同的． 19．长方形的周长 40cm，长与宽的比是 5 : 3，面积是 ( ) A． 2375cm B． 215cm C． 293.75cm D． 245cm 【分析】根据题意，长方形的周长为 40厘米，则长与宽的和为： 40 2 20  （厘米），根据按比分配原则， 求其长和宽分别为： 20 (5 3) 2.5   （厘米）， 2.5 5 12.5  （厘米）， 2.5 3 7.5  （厘米）．利用长方形面 积公式： S ab ，求其面积为：12.5 7.5 93.75  （平方厘米）． 【解答】解： 40 2 (5 3)   20 8  2.5 （厘米） (2.5 5) (2.5 3)   12.5 7.5  93.75 （平方厘米） 答：长方形的面积为 93.75平方厘米． 故选：C． 【点评】本题主要考查比的应用，关键利用按比分配原则求出长方形的长和宽． 20．某商店有 500台电视机，第一天卖掉了 20%，第二天又进了一部分电视机，进的台数是第一天剩余台 数的 20%，现在电视机有 ( )台． A．540 B．520 C．500 D．480 【分析】把原来的台数看成单位“1”，卖掉后的台数是原来的台数的 (1 20%) ；再把卖掉后的台数为单位 “1”，现在的台数是卖掉后的台数的 (1 20%) ；运用乘法求出现在的台数占原来台数的分率为 (1 20%) (1 20%)   ，已知原有 500台，运用乘法即可求出现在的台数． 【解答】解： 500 (1 20%) (1 20%)    400 1.2  480 （台 ) 答：现在电视机有 480台． 故选： D．[来源:学科网] 【点评】解答此题的关键是分清两个不同的单位“1”，已知单位“1”的量，求它的百分之几是多少用乘法 计算． 21．一个圆形钟面，分针长 6厘米，经过 60分钟，分针针尖走过了 ( )厘米． A．37.68 B．21.4 C．28.26 D．25.12 【分析】60分钟，分针正好转过了钟面的一圈，所以分针针尖所走的路程就是以分针的长度 6厘米为半径 的圆的周长，由此利用圆的周长公式即可解答． 【解答】解： 3.14 6 2  18.84 2  37.68 （厘米） 答：分针针尖走过了 37.68厘米． 故选： A． 【点评】此题主要考查的是圆的周长公式的应用． 四．计算题（共 4小题，共 32 分） 22．直接写得数．（共 10 小题，每小题 0.5 分，共 5 分） 3.6 4  1 1 6 2   215 3   1 25% 4   3 3 7   25% 4  324 4   3 9 8 8   2 2 0 3 3    1 1 1 1 3 4 3 4     【分析】根据小数、分数减法、乘除法运算的计算法则计算即可求解．注意 1 1 1 1 3 4 3 4    变形为 1 1 1 1( ) ( ) 3 3 4 4    计算． 【解答】解： 3.6 4 0.9  1 1 1 6 2 12   215 10 3   1 125% 4 16   3 13 7 7   25% 4 1  324 18 4   3 9 1 8 8 3   2 2 20 3 3 3    1 1 1 1 1 3 4 3 4 16     [来源:Z.xx.k.Com] 【点评】考查了小数、分数减法、乘除法运算，关键是熟练掌握计算法则正确进行计算． 23．怎样简便就怎样算．（每小题 3分，共 12分） （1） 3 3 4[4 ( )] 4 8 29    （2） 43.5 6.5 0.8 5    （3） 5 1 12 4 17 4 17    （4） 4 1 7 7( ) 5 4 3 10    【分析】（1）先算小括号里面的减法，再算中括号里面的减法，最后算乘法； （2）、（3）根据乘法分配律进行简算； （4）先算小括号里面的加法，再算除法，最后算括号外面的加法． 【解答】解：（1） 3 3 4[4 ( )] 4 8 29    3 4[4 ] 8 29    29 4 8 29   1 2  （2） 43.5 6.5 0.8 5    3.5 0.8 6.5 0.8    (3.5 6.5) 0.8   10 0.8  8 （3） 5 1 12 4 17 4 17    5 1 12 1 17 4 17 4     5 12 1( ) 17 17 4    11 4   1 4  （4） 4 1 7 7( ) 5 4 3 10    21 7 7 20 3 10    9 7 20 10   23 20  【点评】考查了运算定律与简便运算，四则混合运算．注意运算顺序和运算法则，灵活运用所学的运算定 律进行简便计算． 24．解方程．（每小题 3分，共 9分） 2 50% 300 3 x x  60% 35% 125x x  4.1 30% 2x  【分析】（1）首先化简，然后根据等式的性质，两边同时乘 6 7 即可． （2）首先化简，然后根据等式的性质，两边同时乘 4即可． （3）首先根据等式的性质，两边同时加上 0.3x，然后两边同时减去 2，最后两边同时除以 0.3即可． 【解答】解：（1） 2 50% 300 3 x x  7 300 6 x  7 6 6300 6 7 7 x   1800 7 x  （2） 60% 35% 125x x  0.25 125x  0.25 4 125 4x   500x  （3） 4.1 30% 2x  4.1 0.3 2x  4.1 0.3 0.3 2 0.3x x x    2 0.3 4.1x  2 0.3 2 4.1 2x    0.3 2.1x  0.3 0.3 2.1 0.3x    7x  【点评】此题主要考查了根据等式的性质解方程的能力，即等式两边同时加上或同时减去、同时乘或同时 除以一个数 (0除外），两边仍相等． 25．计算图（1）的周长、图（2）阴影部分的面积．（共 6分） 【分析】（1）半圆的周长 2d d   ；代入数据即可解答． （2）阴影部分的面积等于大圆的面积减去小圆的面积，公式： 2 2 2 2 2 1 2 1( )S r r r r      ． 【解答】解：（1） 3.14 4 2 4   6.28 4  10.28 （厘米） 答：这个半圆的周长是 10.2 8厘米． （2） 3.14 6 6 3.14 2 2     3.14 (36 4)   3.14 32  100.48 （平方厘米） 答：阴影部分的面积是 100.48平方厘米． 【点评】本题考查了半圆的周长和圆环的面积的计算．半圆的周长要加上直径． 五．操作题（共 2小题,4+2=6分） 26．下面每个方格的边长表示 1厘米． （1）画一个长方形，周长是 24厘米，长和宽的比是 2 :1． （2）画一个长方形，面积是 24平方厘米，长和宽的比是 3 : 2． 【分析】（1）根据长方形的周长公式可知：长方形的周长 （长 宽） 2 ，可用 24厘米除以 2得到长与宽 的和，然后再除以 (2 1) 得到长方形的宽，用宽乘 2就是长方形的长；作图即可； （2）长方形的面积是 24平方厘米，长和宽的比是 3 : 2，因此可知长和宽分别是 6 厘米和 4 厘米，由此即 可画图． 【解答】解：（1）长与宽的和为： 24 2 12  （厘米） 宽为：12 (2 1) 4   （厘米） 长为： 4 2 8  （厘米） （2） 4 6 24  （平方厘米） 6 : 4 3 : 2 所以长和宽分别是 6厘米和 4厘米； 作图如下： 【点评】解答此题的关键是根据长方形的周长或面积公式确定长方形的长、宽，然后再进行作图． 27．在方格纸上画出从不同角度看到下面立体图形的形状． 【分析】左边的立体图形由 4个相同的小正方体构成．从正面能看到 3 个正方形，分两行，上行 1 个，下 行 2 个，左齐；从上面能看到 3 个正方形，分两行，上行 2 个，下行 1个，左齐；从右面能看到 3个正方 形，分两行，上行 1 个，下行 2 个，左齐；从左面能看到 3 个正方形，分两行，上行 1 个，下行 2个，右 齐． 【解答】解：在方格纸上画出从不同角度看到下面立体图形的形状． 【点评】本题是考查作简单图形的三视图，能正确辨认从正面、上面、左面（或右面）观察到的简单几何 体的平面图形． 六．应用题（共 6小题，4 分+5 分+4 分+5 分+5 分+4 分= 27 分） 28．果园里有桃树 100棵，梨树的棵数是桃树的 3 5 ，是桔树的 3 4 ．果园里有桔树多少棵？桃树棵数比桔树 多百分之几？ 【分析】先把桃树的棵数看作单位“1”，根据分数乘法的意义，用桃树的棵数乘 3 5 就是梨的棵数．再把梨 树的棵数看作单位“1”，根据分数除法的意义，用梨树的棵数除以 3 4 就是桔树的棵数．求桃树的棵数比桔 树多百分之几，用桃树比桔树多的棵数除以桔树的棵数． 【解答】解： 3 3100 5 4   360 4   80 （棵 ) (100 80) 80  20 80  0.25 25% 答：果园里有桔树 80棵，桃树棵数比桔树多 25%． 【点评】解答此题的关键是根据分数乘、除法的意义求出桔树的棵数．求一个数比另一个数多百分之几， 用这两数之差除以另一个数． 29．筑路队要铺一条公路，第一周铺了全长的 1 4 ，第二周铺了全长的 20%，还剩 220千米没有铺．这条公 路全长有多少千米？ 【分析】把这条公路的全长看作单位“1”，第一周铺了全长的 1 4 ，第二周铺了全长的 20%，还剩 220千米 没有铺，由此可知没有铺的 220米占这条公路的 1(1 20%) 4   ，根据已知的一个数的几分之几（百分之几） 是多少，求这个数，用除法解答． 【解答】解： 1220 (1 20%) 4    1 1220 (1 ) 4 5     11220 20   20220 11   400 （米 ) 答：这条公路全长有 400米． 【点评】解答此类问题，首先找清单位“1”，进一步理清解答思路，列式的顺序，从而较好的解答问题． 30．某天六年级一班出勤的人数是 38人，有 2人缺勤．该班这天的出勤率是多少？ 【分析】先用“ 38 2 ”求出该班总人数，进而根据公式：出勤率出勤的人数 全班总人数 100% ；代入 数值，进行解答． 【解答】解： 38 2 40  （人 )， 38 40 100% 95%   ； 答：出勤率是 95%． 【点评】此题属于百分率问题，计算的结果最大值为100%，都是用一部分数量（或全部数量）除以全部数 量乘百分之百． 31．一个圆形花坛的直径是 6米，现在要扩建花坛，把它的半径增加 1米． （1）花坛的面积比原来增加了多少平方米？ （2）花坛的周长比原来增加多少米？ 【分析】（1）根据题意可知：增加部分的面积是环形，根据环形面积 外圆面积 内圆面积，把数据代入公 式解答． （2）根据圆的周长公式：C d ，把数据代入公式求出大小圆的周长差即可． 【解答】解：（1） 6 2 3  （米 ) 2 23.14 [(3 1) 3 ]   3.14 [16 9]   3.14 7  21.98 （平方米）； 答：花坛的面积比原来增加 21.98平方米． （2） 3.14 (6 0.5 2) 3.14 6     3.14 7 18.84   21.98 18.84  3.14 （米 )； 答：花坛的周长比原来增加 3.14米． 【点评】此题主要考查环形面积公式的灵活运用，以及圆的周长公式的灵活运用，关键是熟记公式． 32．用一根长 72分米的铁丝做一个长方体框架，使它的长、宽、高的比是 4 :3 : 2．如果在这个长方体框架 外面糊一层纸，至少需要多少平方分米的纸？ 【分析】一个长方体长宽高各有 4根，那么长 宽 高的和就是 72除以 4；然后把长宽高的和按照 4 :3 : 2的 比例进行分配，求出这个长方体的长宽高； 求至少需要多少平方分米的纸，就是求这个长方体的表面积，根据长方体的表面积公式求解． 【解答】解： 72 4 18  （分米） 4 3 2 9   418 8 9   （分米） 318 6 9   （分米） 218 4 9   （分米） 8 6 2 8 4 2 6 4 2        96 64 48   208 （平方分米） 答：至少需要 208平方分米的纸． 【点评】解决本题先根据长方体的条数求出长宽高的和，然后再根据按比例分配的方法求出长宽高，再由 长方体的表面积公式求解． 33．六年 ( 1 )班全体同学投票选班长，毎位同学投且只能投一票，得票数最高者当选．下面是全部候选人 得票情况統汁图． （1）当选班长的同学姓名是 吴佳 ． （2）王倩得票数占总票数的 %． （3）如果张力得 4票，那么吴佳得多少票？ 【分析】（1）通过观察扇形统计图可知：当选班长的同学是吴佳． （2）把六年级（1）班的学生人数看作单位“1”，根据减法的意义，用减法求出王倩得票数占总票数的百 分之几． （3）把六年级（1）班的学生人数看作单位“1”，其中张力得了 4票，占总票数的10%，根据已知一个数 的百分之几是多少，求这个数，用除法求出总票数，再根据一个数乘百分数的意义，用乘法解答． 【解答】解：（1）当选班长的同学是吴佳．[来源:学科网 ZXXK] [来源:Zxxk.Com] （1）1 55% 10% 12.5% 22.5%    ； 答：王倩得票数占总票数的 22.5%． （3） 4 10% 55%  4 0.1 0.55   40 0.55  22 （票 ) 答：吴佳得了 22票． 故答案为：吴佳、22.5． 【点评】此题考查的目的是理解掌握扇形统计图的特点及作用，并且能够根据统计图提供的信息，解决有 关的实际问题．