小升初数学总复习知识整理 23页

小升初数学总复习知识整理 一、数的认识 1.数的分类 提示:按不同的标准划分 ,数的分类也会不同。 例如 :按正、负数分 ,数分为正数、 0、负数 ;按整数与分数分 ,数分为整数、分数 (小 数)等。 (1)整数 :像-3 、-2 、-1 、0、1、2、3⋯⋯这样的数统称为整数。整数的个数是无限．．．．．．．． 的．,．没有最小的整数．．．．．．． ,．也没有最大的整数。．．．．．．．．． 数 (2)自然数 :用来表示物体个数的 1、2、3、4⋯⋯叫做自然数。 一个物体也没有 ,用 0 表示 ,0．也是自然数。自然数的个数是无限的．．．．．．．．．．．．．．．． ,．最小的自然数是．．．．．．． 0,．．没有最大的自然数。自．．．．．．．．．． 然数是整数的一部分．．．．．．．．． ,．正整数和．．．． 0．都是自然数。．．．．．． 提示:0 表示一个物体也没有 ;0 是正、 负数的分界点 ;0 表示起点 (如 0 刻度 );计数时 ,0 起占位作用。 (3)分数 :把单位 “．．．．1．”平均分成若干份．．．．．．．． ,．表示这样的一份或者几份的数叫做分数．．．．．．．．．．．．．．．．． ,．表示．． 这样一份的数就是这个分数的分数单位。．．．．．．．．．．．．．．．．．． 一个分数的分母是几 ,它的分数单位就是几分 之一,分子是几 ,它就有几个这样的分数单位。 注意 :带分数只有化成假分数后 ,它的分子才能表示这个带分数的分数单位的个数。 (4)百分数 :表示一个数是另一个数百分之几的数叫做百分数．．．．．．．．．．．．．．．．．．．．． ,．也叫百分率或百分比。．．．．．．．．． ． 百分数的计数单位是．．．．．．．．． 1%．．。．百分数是一种特殊的分数 ,通常不写成分数形式 ,而是在原来 的分子后面加上百分号“ %”来表示。 (5)分数和百分数的关系 :分数既可以表示一个数．．．．．．．．．． ,．也可以表示两个数的比．．．．．．．．．． ;．而百分数．．．． 只表示一个数占另一个数的百分比．．．．．．．．．．．．．．． ,．不能用来表示具体的数。 分数后面可以带单位名称．．．．．．．．．．．．．．．．．．．．．． ,． 而百分数后面不能带单位名称。．．．．．．．．．．．．．． 例如 : 写成百分数是 59%, 可以表示 59 ∶100, 也可以表示一个数量 ,如 米, 吨等,而 59% 只表示一个数和另一个数的关系 ,后面不能带单位名称。 (6)小数 :像．0.1．．．、．0.2．．．、．3.14．．．．、．10.007．．．．．．⋯⋯这样用来表示十分之几、百分之几、千分．．．．．．．．．．．．．．．．．．．． 之几⋯⋯的数叫做小数。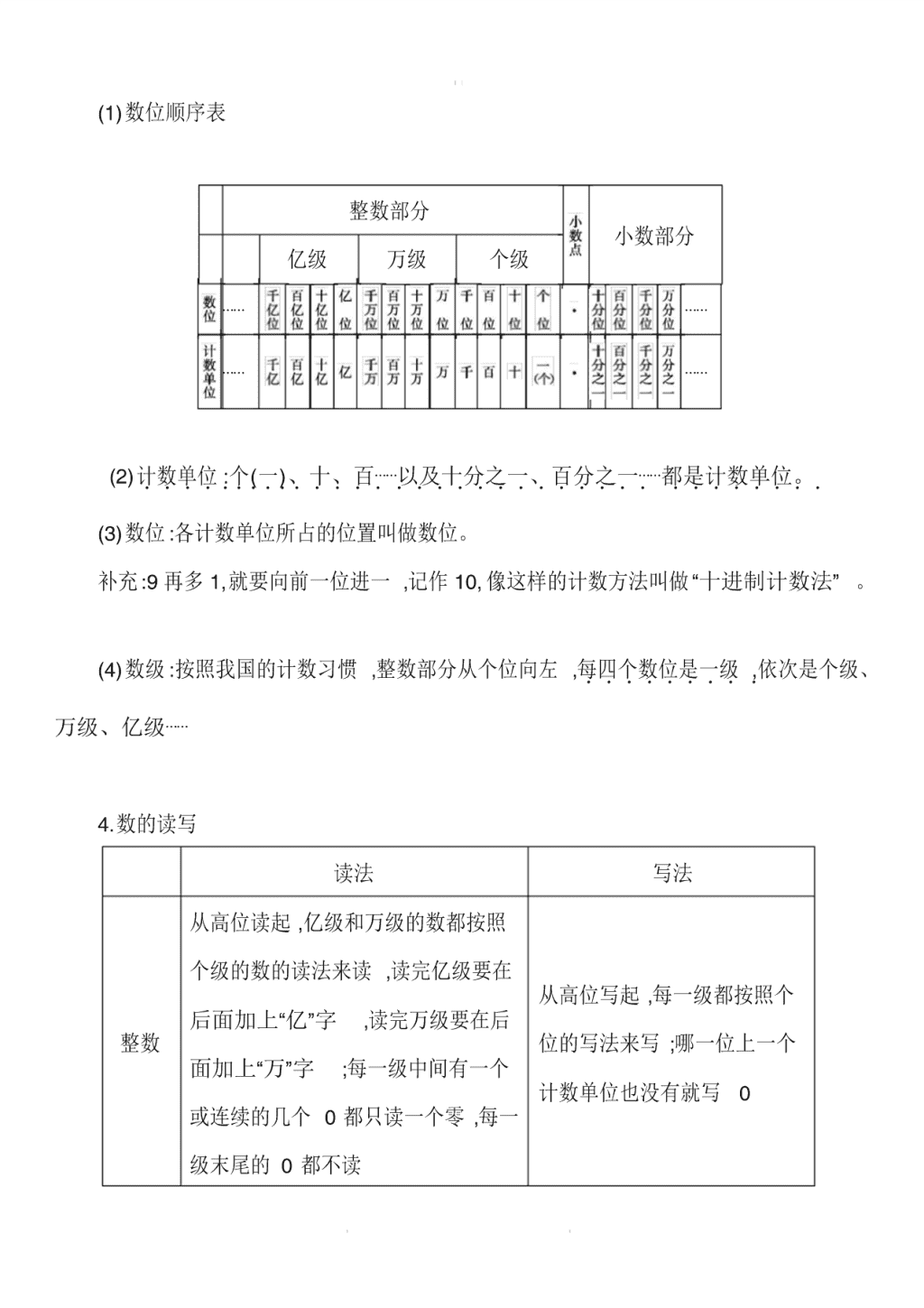．．．．．．．．．．． 3.计数单位和数位 (1)数位顺序表 整数部分 小数部分 亿级 万级 个级 ⋯⋯ ⋯⋯ ⋯⋯ ⋯⋯ (2)计数单位．．．．:．个．(．一．)．、十、百⋯⋯以及十分之一、百分之一⋯⋯都是计数单位。．．．．．．．．．．．．．．．．．． ．．．．．．．． (3)数位 :各计数单位所占的位置叫做数位。 补充 :9 再多 1,就要向前一位进一 ,记作 10, 像这样的计数方法叫做 “十进制计数法” 。 (4)数级 :按照我国的计数习惯 ,整数部分从个位向左 ,每四个数位是一级．．．．．．．． ,．依次是个级、 万级、亿级⋯⋯ 4.数的读写 读法 写法 整数 从高位读起 ,亿级和万级的数都按照 个级的数的读法来读 ,读完亿级要在 后面加上“亿”字 ,读完万级要在后 面加上“万”字 ;每一级中间有一个 或连续的几个 0 都只读一个零 ,每一 级末尾的 0 都不读 从高位写起 ,每一级都按照个 位的写法来写 ;哪一位上一个 计数单位也没有就写 0 分数 整数部分按照整数的读法来读 ,读完 后加上个“又”字 ;分数部分先读分 母,加上“分之” ,后面再读分子 整数部分按照整数的写法来 写 ,“又”字不用写 ,分数部分 先读的是分母 ,写在下面 ,后读 的是分子 ,写在上面 ,中间用分 数线隔开 百分数 先读“百分之” ,再读百分号前面的 数 分子是几就写几 ,然后在后面 写上百分号“ %” 小数 整数部分按照整数的读法来读 ,小数 点读作“点” ,小数部分从左向右是 几就读几 整数部分按照整数的写法来 写 ,“点”写作“ .”,小数部分 从左向右读几就写几 注意 :读数和写数都从高位起 ,读数要写成文字形式 ,写数要写成阿拉伯数字 ,例如 ,3 1403 7000 读作 :三亿一千四百零三万七千 ;一千七百零七万五千四百 写作 :1707 5400;60 读作 :六十又七分之五 ;三又十二分之七写作 :3 ;35% 读作百分之三十五 ;百分 之十五点七写作 :15.7%;18.003 读作 :十八点零零三 ;零点六一八写作 :0.618 。 5.大数的改写 (1)把多位数改写成用“万”或 “亿”作单位的数 ,在万位或亿位的后面点上小数点 , 省略小数部分末尾的 0,并在后面写上“万”或“亿”字 ,中间用“ = ”连接。 (2)省略尾数改写成近似数 :用“四舍五入” 法省略万位或亿位后面的尾数 ,并在这个 数的后面写“万”或“亿”字 ,中间用“≈”连接。 6.小数的近似数 要求把小数保留到哪一位 ,就把哪一位后面的数用 “四舍五入” 法省略 ,中间用 “≈” 连接。 提示:在读、写、改写数时 ,原数如果有单位名称 ,读数、写数、改写的结果也要加上 相应的单位名称。 易错点 :要区分“改写”和“省略”的含义。改写是求准确值 ,“省略”是用“四舍 五入”法求近似数。 7.假分数与带分数、整数之间的互化 (1)假分数化成整数或带分数 :用假分数的分子除以分母 ,如果能够整除 ,所得的商就 是这个假分数化成的整数 ;如果不能整除 ,商的整数部分就是带分数的整数部分 ,余数就 是分数部分的分子 ,原分母不变。 (2)整数化成假分数 :用指定的分母作分母 ,用整数乘分母的积作分子。 (3)带分数化成假分数 :用整数部分乘分母的积加上分数部分的分子作分子 ,原分母 不变。 例如 :把 和 改写成整数或带分数。 12 ÷3=4 =4 =1 例如 :5= = 6 = = 8.分数、小数、百分数之间的互化 小数化成分数 :先改写成分母是 10 、100 、1000 ⋯⋯的分数,再约分 ;分数化成小数 , 用分子除以分母 ;小数化成百分数 ,把小数的小数点向右移动两位 ,并在后面加上百分号 ; 百分数化成小数 ,把百分号去掉 ,并把小数点向左移动两位 ;分数化成百分数 ,先把分数改 写成小数 ,再把小数改写成百分数 ;百分数化成分数 ,先把百分数改写成分母是 100 的分 数,再化简。 例如 : 0.52= = =3 ÷8=0.375 0.32=32% 3.5%=0.035 =0.75=75% 62.5%= . = 9.判断一个分数能否化成有限小数的方法 先看这个分数是不是最简分数 ,不是最简分数的要化成最简分数 ;再看最简分数的 分母,如果分母中只有质因数 2 或 5,这个分数就能化成有限小数 ;如果分母中含有 2 和 5 以外的其他质因数 ,就不能化成有限小数。 提示:判断分母是否只含有质因数 2 或 5,可以参照“ 2 和 5 的倍数的特征”进行分 析。 10. 数的大小比较 (1)整数的大小比较 :先看位数 ,位数多的数大 ;位数相同 ,从高位比起 ,相同数位上的 数大的那个数就大。 (2)分数的大小比较 :先比较整数部分 ,整数部分大的那个数就大 ;整数部分相同比较 十分位 ,十分位上数大的那个数就大 ;十分位相同 ,比较百分位 ,百分位上数大的那个数就 大;百分位相同 ,比较千分位⋯⋯ (3)真分数、假分数和整数部分相同的带分数的大小比较 :分母相同 ,分子大的分数大 ; 分子相同 ,分母小的分数大 ;分子分母都不同 ,通分化成同分母或同分子分数后再比较 ;假 分数大于真分数。 整数部分不同的带分数 ,整数部分大的分数大。 例如 :7856>856 6933>6920 例如 :62.57>52.75 4.256>4.252 例如 : > > > 3 >1 提示:比较小数、分数和百分数的大小时 ,通常把分数和百分数化成小数进行比较 , 最后的结果一定要用原数。 11. 用直线上的点表示数 (数轴) (1)小学阶段学过的数都可以用直线上的点来表示。例如 : (2)在这条直线上 ,0 是正数和负数的分界点 ,箭头方向表示正数的方向 ,每一大格的 长度都相等。 提示:用数轴上的点可以比较数的大小。 数轴上表示数的点的位置越往右 ,表示的数 越大,点的位置越往左 ,表示的数越小。 12. 因数与倍数 如果 a÷b=c(a 、b、c 都是整数 ,且 b ≠0),就说 a 是 b 和 c 的倍数 ,b 和 c 是 a 的因数。 如果一个数既是 a 的因数 ,又是 b 的因数 ,那它就是 a 和 b 的公因数。 如果一个数既是 a 的倍数 ,又是 b 的倍数 ,那它就是 a 和 b 的公倍数。 注意 :一个数的因数的个数是有限的 ,最小的因数是 1,最大的因数是它本身。 一个数 的倍数的个数是无限的 ,最小的倍数是它本身 ,没有最大的倍数。 13. 奇数与偶数 整数中 ,能被 2 整除的数是偶数 ,不能被 2 整除的数是奇数。 注意 :一个自然数不是奇数 ,就是偶数。 14. 质数与合数 质数又称素数．．．．．．,．指在大于．．．． 1．的自然数中．．．．．,．除了．．1．和它本身外．．．．．,．没有其他因数的数。．．．．．．．．． 合数是指自然数中除了．．．．．．．．．． 1．和它本身之外．．．．．．,．还有其他因数的数。．．．．．．．．． 重点 :1 既不是质数 ,也不是合数。 最小的质数是 2,它是唯一的偶质数 ;最小的合数是 4。 15.2 、3、5 的倍数的特征 (1)2 的倍数的特征 :个位上的数是 0、2、4、6、8。 (2)3 的倍数的特征 :各个数位上的数字的和是 3 的倍数。 (3)5 的倍数的特征 :个位上的数是 0 或 5。 16. 分数的基本性质．．．．．．． :．分数的分子和分母同时乘或除以相同的数．．．．．．．．．．．．．．．．．． (0．．除外．．),．．分数的大小．．．．． 不变。．．．利用分数的基本性质可以进行分数的通分和化简。 17. 小数的性质．．．．．:．在小数的末尾添上．．．．．．．． 0．或者去掉．．．． 0,．．小数的大小不变。．．．．．．．． 利用小数的性 质可以进行小数的化简和改写。 提示:在小数的末尾添上 0 或者去掉 0,小数的大小不变 ,计数单位却不同。例如 :3.2 的计数单位是 0.1,3.200 的计数单位是 0.001 。 18. 小数点位置移动引起小数的大小变化 ．．．．．．．．．．．．．．．． 小数点向右移动一位．．．．．．．．． ,．小数就扩大到原来的．．．．．．．．． 10．．倍 ．;．小数点向右移动两位．．．．．．．．． ,．小数就扩大．．．．． 到原来的．．．． 100．．．倍 ．;．小数点向右移动三位．．．．．．．．． ,．小数就扩大到原来的．．．．．．．．． 1000．．．．倍⋯⋯．．． 小数点向左移动一位 ,小数就缩小到原来的 ;小数点向左移动两位 ,小数就缩小到 原来的 ;小数点向左移动三位 ,小数就缩小到原来的 。 例如 :32.1 的小数点向右移动一位是 321, 是原数的 10 倍 ;32.1 的小数点向左移动 一位是 3.21, 是原数的 。 二、数的运算 1.四则运算 加法 :把两个数合成一个数的运算。 减法 :已知两个数的和与其中的一个加数 ,求另一个加数的运算。 乘法 :求几个相同加数的和的简便运算。 除法 :已知两个乘数的积与其中一个乘数 ,求另一个乘数的运算。 提示:加法和减法互为逆运算 ;乘法和除法互为逆运算。 2.四则运算中各部分之间的关系 加法 :加数．．+．加数．．=．和 ．;．一个加数．．．．=．和 ．-．另一个加数。．．．．．． 减法 :被减数．．．-．减数．．=．差．;．被减数．．．=．差．+．减数．．;．减数．．=．被减数．．．-．差。．． 乘法 :乘数．．×．乘数．．=．积 ．;．一个乘数．．．．=．积 ．÷．另一个乘数。．．．．．． 除法 :被除数．．．÷．除数．．=．商．;．被除数．．．=．商．×．除数．．;．除数．．=．被除数．．．÷．商。．． 提示:应用四则运算中各部分之间的关系可以对四则运算进行验算。 3.四则混合运算的顺序 没有括号的算式．．．．．．． ,．同级运算从左向右算．．．．．．．．． ;．含两级运算的．．．．．．,．先算乘除．．．．,．后算加减．．．．;．有括号的．．．． 算式．．,．先算小括号里面的．．．．．．．． ,．再算中括号里面的．．．．．．．． ,．最后算括号外面的。．．．．．．．．． 提示:加减法是同一级运算 ,称为一级运算 ;乘除法是同一级运算 ,称为二级运算。 4.运算定律 用字母表示 名称 加法交换律 a+b=b+a 加法结合律 (a+b)+c=a+(b+c) 乘法交换律 a×b=b ×a 乘法结合律 (a×b) ×c=a ×(b×c) 乘法分配律 (a+b) ×c=a ×c+b ×c a×(b+c)=a ×b+a ×c 5.运算性质 (1)减法的运算性质 :a-b-c=a-(b+c) a-b+c=a-(b-c) (2)除法的运算性质 :a÷b÷c=a ÷(b ×c) a÷b×c=a ÷(b÷c) (a+b) ÷c=a ÷c+b ÷c (a-b) ÷c=a ÷c-b ÷c 提示:在运算中灵活地运用运算定律和减法、 除法的运算性质 ,可以使运算更加简便。 6.典型的数学问题 (1)相遇问题 :路程÷(甲速 + 乙速)= 相遇时间 (甲速 + 乙速)×相遇时间 = 路程 提示:路程÷相遇时间 -甲速 = 乙速 (2)追击问题 :(假设甲速大于乙速 )甲与乙的距离÷ (甲速 -乙速)= 追上时间 (甲速 -乙速)×追上时间 = 甲与乙的距离 (3)工程问题 :工作总量÷工作效率 = 工作时间 工作总量÷工作时间 = 工作效率 工作效率×工作时间 = 工作总量 提示:在 “工程问题” 中常见 “甲、 乙合作多长时间能完成工作 ?”解题的方法是 “工 作总量÷ (甲的工作效率 + 乙的工作效率 )= 工作时间”。 (4)和差问题 :(和 + 差 )÷2= 大数 大数-差 = 小数 (和 -差 )÷2= 小数 小数 + 差 = 大数 和 -小数= 大数 (5)鸡兔同笼问题 :假设全是鸡 ,(总腿数 -总头数× 2)÷(4-2)= 兔的只数 ;假设全是 兔 ,(总头数× 4- 总腿数 )÷(4-2)= 鸡的只数。 提示:鸡兔同笼问题也可以用列表法、画图法、列方程等方法解答。 三、式与方程 1.用字母或含有字母的式子可以简明地表示数 ,也可以表示数量关系 ,运算定律和 计算公式等。 2.等式 :表示相等关系的式子叫做等式。 3.方程 :含有未知数的等式叫做方程。使方程左右两边相等的未知数的值 ,叫做方程 的解。求方程的解的过程叫做解方程。 提示:所有的方程都是等式 ,但等式不一定是方程。 4.等式的性质．．．．．:．等式的两边同时加上．．．．．．．．． (．或减去．．．)．同一个数．．．．,．等式仍然成立．．．．．．;．等式的两边同．．．．．． 时乘 ．．(．或除以．．．)．同一个数．．．．(0．．除外．．),．．等式仍然成立。．．．．．．． 提示:等式的性质是解方程的依据。 5.列方程解应用题的一般步骤．．．．．．．．．．．． :．①理解题意 ,找出题中的等量关系 ;②把未知量设成 未知数 ,根据等量关系列出方程 ;③根据等式的性质求出未知数的值 ;④检验 ,并写出答语。 四、比和比例 1.比和比例的区别 比 比例 意义 两个数相除又叫做两个数的比 表示两个比相等的式子 各部分 名称 基本性 质 比的前项和后项同时乘或除以 相同的数 (0 除外),比值不变 在比例里 ,两个外项的积 等于两个内项的积 2.比与分数、除法的联系 各部分名称 例子 分数 分子 分数线 分母 分数值 除法 被除数 除号 除数 商 5÷8= 比 前项 比号 后项 比值 5∶8= 提示:比和比例、比、分数和除法都既有联系 ,又有区别。把握好比和比例的关系 , 可以提高我们分析问题和解决问题的能力。 提示:灵活运用比和比例及比、 分数和除法之间的关系 ,可以将分数应用题转化为按 比分配的应用题或是可以用解比例的方法解答的问题 ,也可以将按比分配或需要列比例 式解答的应用题转化成分数应用题解答。 五、图形的认识与测量 1.图形的分类 补充 :等腰三角形是有两条边相等的三角形。 等边三角形是特殊的等腰三角形 ,它的 三条边都相等。 注意 :梯形中还有两种比较特殊的情况 :等腰梯形和直角梯形。 等腰梯形是两个腰相 等的梯形 ;直角梯形是有两个直角的梯形。 图形 2.直线、射线、线段 把线段的两端无限延伸 ,就得到一条直线。 直线没有端点 ,可以向两端无限延伸 ,不能 度量长度。 把线段的一端无限延伸 ,就得到一条射线。 射线只有一个端点 ,可以向另一端无限延 伸 ,不能度量长度。 直线上两点间的一段叫做线段。线段有两个端点 ,可以度量长度。 注意 :射线和线段都是直线的一部分。 3.同一平面内两条直线的位置关系 ．．．．．．．．．．．．．． :．相交和平行。．．．．．． 4.垂直和垂线 :如果两条直线相交成直角．．．．．．．．．．． ,．就说这两条直线互相垂直．．．．．．．．．．． ,．其中一条直线．．．．．． 叫做另一条直线的垂线．．．．．．．．．． ,．它们的交点叫做垂足。．．．．．．．．．． 5.平行线 :在同一平面内不相交的两条直线叫做平行线。．．．．．．．．．．．．．．．．．．．． 平行线之间的距离处处相 等。 提示:在同一平面内的两条直线不是相交就是平行。垂直是相交的特例。 6.角的分类 锐角 直角 钝角 平角 周角 小于 90 ° 90° 大于 90° 小于 180° 180 ° 360 ° 注意 :1 周角 =2 平角 =4 直角 平角的两条边在一条直线上 ,但平角不是直线 ,它有顶点 ,它是一个角。 7.三角形的特征 三角形有．．．． 3．个顶点、．．．．3．条边、．．．3．个角。三角形的内角和是．．．．．．．．．．． 180．．．°。． 在一个三角形中．．．．．．． ,．任意两边的和都大于第三边．．．．．．．．．．．． ,．任意两边的差都小于第三边。 三角形．．．．．．．．．．．．．．．． 具有稳定性。．．．．．． 提示:运用三角形三边之间的关系 ,可以判断三条线段或三根小棒能否组成三角形。 8.四边形的特征 边 角 长方形 两组对边分别平行且相 等 四个角都是直角 正方形 两组对边分别平行 ,四条 边都相等 四个角都是直角 平行四边形 两组对边分别平行且相 等 对角相等 梯形 只有一组对边平行 —— 9.四边形的分类 注意 :长方形和正方形是特殊的平行四边形 ,正方形是特殊的长方形。 10. 平面图形的周长与面积 文字公式 字母公式 长方形 长方形周长 =( 长 + 宽 )×2 长方形面积 = 长×宽 C=2(a+b) S=ab 正方形 正方形周长 = 边长× 4 正方形面积 = 边长×边长 C=4a S=a 2 平行四边形 平行四边形面积 = 底×高 S=ah 三角形 三角形面积 = 底×高÷ 2 S= ah 梯形 梯形面积 =( 上底 + 下底 )×高÷2 S= (a+b)h 圆 圆的周长 = 圆周率×直径 圆的周长 = 圆周率×半径× 2 圆的面积 = 圆周率×半径的平方 C= πd C=2 πr S= πr 2 提示:我们经常会遇到求不规则图形的周长或面积的情况 ,可以运用转化和迁移的 数学思想 ,把不规则图形转化成我们学过的图形 ,再计算它们的周长或面积。 11. 长方体和正方体的特征 相同点 不同点 面 棱长 长方 体 都有 6 个面、 8 个 顶点、 12 条棱 相对的面的形状、 大小都相等 相对的 4 条棱互相 平行并且长度相等 正方 体 6 个面都是完全相 同的正方形 12 条棱长度相等 提示:长方体的所有特征 ,正方体都具备 ,所不同的是正方体有 6 个完全相同的面 ,12 条棱长度都相等 ,正方体是特殊的长方体。 12. 立体图形的表面积与体积 表面积计算公式 体积计算公式 S 长方体 =2(ab+ah+bh) V 长方体 =abh V=Sh S 正方体 =6a 2 V 正方体 =a 3 S 圆柱 =2 πr 2+2 πrh V 圆柱 = πr 2h —— V 圆锥 = πr2h V 圆锥 = Sh 注意 :体积是指物体所占空间的大小 ,求物体的体积是从物体外部测量长、宽、高等数据 的;容积是指一个容器所能容纳的物体的体积 ,求物体的容积要从物体的内部测量长、 宽、 高等数据。 13. 圆柱与圆锥的关系 : 当圆柱与圆锥等底等高时，圆柱的体积是圆锥体积的 3 倍；当圆柱与圆锥等体积 及等高时，圆锥的底面积是圆柱底面积的 3 倍；当圆柱与圆锥等体积和等底时，圆锥 的高是圆柱高的 3 倍。 14. 常见的计量单位与进率 (1)长度单位 :1 厘米=10 毫米 1 分米=10 厘米 1 米=10 分米=100 厘米 1 千米 =1000 米 (2)面积单位 :1 平方厘米 =100 平方毫米 1 平方分米 =100 平方厘米 1 平方米 =100 平方分米 =10000 平方厘米 1 公顷 =10000 平方米 1 平方千米 =100 公顷 =1000000 平方米 (3)体积单位 :1 立方厘米 =1000 立方毫米 1 立方分米 =1000 立方厘米 1 立方米 =1000 立方分米 =1000000 立方厘米 (4)容积单位 :毫升 (mL) 升(L) 立方米 (m 3) 1 升=1 立方分米 1 毫升 =1 立方厘米 1 升=1000 毫升 1 立方米 =1000 升 15. 单位名数的互化方法 (1)低级单位名数化为高级单位名数除以进率 ;高级单位名数化为低级单位名数乘 进率。 (2)复名数改写为高级单位的单名数 ,用复名数的低级单位除以进率 ,再加上复名数 的高级单位。 (3)复名数改写为低级单位的单名数 ,用复名数的高级单位乘进率 ,再加上复名数的 低级单位。 (4)低级单位单名数改写为复名数 ,用单名数除以进率的商的整数部分做复名数的 高级单位 ,余数做复名数的低级单位。 (5)高级单位单名数改写为复名数 ,整数部分做复名数的高级单位 ,小数部分乘进率 做复名数的低级单位。 提示:在比较单位名数的大小时 ,只有相同的单位才能在一起比较 ;单位不同时 ,要化 成相同的单位再进行比较。 六、图形的运动 1.平移 :物体或图形在同一平面内沿直线运动 ,物体或图形的形状、大小、方向都不．．．．．．．．．．．．．．．． 发生改变．．．．,．只是位置发生变化 ．．．．．．．． 。 2.旋转 :物体或图形绕着一个点或一个轴所发生的运动 ,叫做旋转。旋转不改变物体．．．．．．． 的形状和大小．．．．．．,．只改变物体的方向．．．．．．．． 。 提示:平移只改变物体的位置 ,旋转只改变物体的方向。 3.轴对称 :如果一个图形沿着一条直线对折．．．．．．．．．．．．．． ,．两侧的图形能够完全重合．．．．．．．．．．． ,．这个图形就．．．．． 叫做轴对称图形．．．．．．． ,．折痕所在的直线叫做对称轴．．．．．．．．．．．． 。 4.图形的放大和缩小 :把一个图形的各边按一定比例进行放大或缩小 ,从而得到该 图形的放大图或缩小图。 提示:一个图形的放大图或缩小图与原图形相比较 ,形状相同 ,大小不同。 七、图形与位置 1.平面图上通常都是按“上北、下南、左西、右东”来确定方位的．．．．．．．．．．．．．．．．．．．．．．．．．．．． ,．还有东南、东．．．．．． 北、西南、西北四个方向。．．．．．．．．．．．． 2.确定物体方向的两个要素 :方向和距离．．．．．。 3.用数对表示物体的位置 ,数对的第一个数表示在第几列．．．．．．．．．．．．． ,．第二个数表示在第几行．．．．．．．．．． ,． 两个数之间要用逗号隔开 ,并用括号把这个数对括起来。 提示:对照数对在方格纸上找物体的位置时 ,先根据数对的第一个数找到所在的列 , 再根据数对的第二个数找到这一列的第几行 ,行和列的交点就是这个数对所对应的物体 的位置。 八、统计与概率 1.统计表的种类 (1)单式统计表 :只有一组统计项目的统计表。 (2)复式统计表 :有两组或两组以上统计项目的统计表。 2.统计图的种类与特点 统计图种 类 表现形式 特点 条形统计 图 用条形的长短表示 数量的多少 直观表示数量的多少和不同数据的 差异 折线统计 图 用折线上的点表示 数量的增减变化 不仅能清楚地表示数量的多少 ,还能 直观地反映数量的增减变化趋势 扇形统计 图 用整个圆和圆内的 扇形表示各部分数 量占总数的百分比 直观表示各部分数量与总数量之间 的关系 提示:每种统计图的表现形式不同 ,特点也不同 ,应用时要根据数据的特点和需要选 择合适的统计图。 3.平均数 :平均数是表示一组数据平均趋势的数 ,它反映一组数据的平均水平 ,但它 容易受极端数据的影响。 提示:求平均数的方法 :一组数据的总和÷这组数据的个数 = 这组数据的平均数。 4.可能性 :生活中 ,有些事件的发生是不确定的 ,一般用“可能发生”来描述 ;有些事 件的发生是确定的 ,一般用“一定”或“不可能”来描述。 提示:判断每种事件的可能性是否相等 ,可以确定方案规则是否公平。 九、数学思考 1.如果有 n 个点 ,每两个点连一条线段 ,一共能连出 1+2+3+ ⋯⋯+(n-1) 条线段。 2.如果 a=b,b=c, 那么 a=c, 这就是等量代换。 十、综合与实践 1.绿色出行 :绿色出行是指采取相对环保的出行方式 ,即节约能源、提高能效、减少 污染、有益健康、兼顾效率的出行方式 ,如乘坐公共汽车、地铁等公共交通工具 ,骑自行 车等。通过碳减排实现资源的可持续利用 ,促进环境保护 ,减少环境污染。 提示:对城市的发展来说 ,绿色出行可以缓解交通拥堵 ,降低空气污染 ,减少交通事故 ;对市 民来说 ,它可以减少对汽车的使用和依赖 ,改善居住环境 ,促进身体健康。 2.制定旅游计划的内容 确定景点 ,选好路线 ;具体、合理地做好时间安排 ;安排住宿、交通工具 ;做好旅游费 用预算 ,旅游费用包括交通费、食宿费、景点门票费、购物费用等。 提示:旅游前应制定切实可行的计划 ,对各方面做周密的安排 ,旅游过程中要按照旅 游计划游览 ,也可随时加以调整。 3.国家邮政局关于信函邮资的收取标准 业务 种类 计费单位 资费标准 / 元 本埠资费 外埠资费 信函 首重 100g 内,每重 20g( 不足 20g 按 20g 计算 ) 0.80 1.20 续重 101~2000g 每重 100g( 不足 100g 按 100g 计算) 1.20 2.00 4.邮资的计算方法 本埠 外埠 不足 20g 0.80 1.20 1-100g 信函质量除以 20 的商(进 一法取整数 )×0.8 信函质量除以 20 的商(进 一法取整数 )×1.20 100g 以上 100 ÷20×0.8+( 信函质 量-100) 除以 20 的商(进 一法取整数 )×1.20 100 ÷20 ×0.8+( 信函质 量-100) 除以 20 的商(进 一法取整数 )×2.00 提示:邮票是邮件的发送者为邮政服务付费的一种证明。邮票分为普通邮票、纪念 邮票等。 提示:本埠是指本市区 ,外埠是指外市区。 5.在“有趣的平衡”中 ,要使竹竿保持平衡 ,必须使“左边的刻度数×棋子数 = 右边 的刻度数×棋子数”。 6.当一边的刻度数和棋子数保持不变时 ,另一边的刻度数和棋子数成反比例关系。 提示:竹竿的平衡规律反映的是物理中的“杠杆原理”。生活中的跷跷板、起钉锤 等都应用了“杠杆原理”。