六年级上册数学青岛六三制知识要点 16页

一 小手艺展示——分数乘法 一、分数乘法的意义 1. 分数乘整数的意义:求几个相同(分数)加数和的简 便运算。 2. 一个数乘分数的意义:表示这个数的几分之几是多 少。 例如:6× 512,表示 6的 512的和。 27×78,表示27的78是多少。 二、分数乘法的计算法则 1.分数乘整数的计算方法:分子与整数相乘,分母不 变。 例如: 6× 512=6×512 =52 2.分数乘分数的计算方法:用分子相乘的积作分子,分 母相乘的积作分母。 例如: 27×78=2×77×8=14 (1)分数化简的方法:分子、分母同时除以它们的 大 公因数。 (2)在乘的过程中约分,是把分子、分母中,两个可以同 时约分的数先画去,再分别在它们的上、下方写出约分后的 数。(约分后分子和分母必须不再含有公因数,这样计算后 的结果才是 简分数) 三、分数乘法的特点 比较积和因数的大小: (1)一个数(0除外)乘比 1大的数,积就大于这个数。 (2)一个数(0除外)乘比 1小的数,积就小于这个数。 (3)一个数(0除外)乘 1,积就等于这个数。 四、倒数 1.倒数的意义。 乘积是 1的两个数互为倒数。倒数表示两个数之间的 关系,这两个数是相互依存的,不能单独存在。 2.求一个数倒数的方法。 (1)求一个数的倒数(0除外),就是把这个数的分子、分 母交换位置。 (2)求小数的倒数的方法:把小数化为分数后再交换位 置。 3.1的倒数是 1,0没有倒数。 4.真分数的倒数一定大于 1,假分数的倒数小于或等 于 1,一个非 0自然数的倒数一定小于 1。 例如:23×3,表示:3个23 相加 的和。 注意:得到的结果要化到 简。 分数乘整数时,可以把分数 看作分母是 1的假分数,进行约 分计算。 分子、分母是互质数的分数 叫作 简分数。 如23、34都叫作 简分数。 0与任何数相乘的积都等于 0。 如果几个不为 0的数与不 同分数相乘的积相等,那么与大 分数相乘的因数反而小,与小分 数相乘的因数反而大。 强调:互为倒数,即倒数是两 个数的关系,它们互相依存,倒数 不能单独存在。 找单位“1”的量:在含有分数 (分率)的语句中,感悟哪个是整 体,把谁给平均分了,分率前面对 第1页 五、解决实际中的分数乘法问题 1.分数应用题一般解题步骤。 (1)找出含有分率的关键句。 (2)找出单位“1”的量。 (3)根据线段图写出等量关系式:单位“1”的量×对应分 率=对应量。 (4)根据已知条件和问题列式解答。 2.乘法应用题有关概念。 (1)乘法应用题的解题思路:已知一个数,求这个数的几 分之几是多少? (2)找单位“1”的方法:从含有分数的关键句中找,注意 “的”前“比”后的规则。当句子中的单位“1”不明显时,把原来 的量看作单位“1”。 3. 分数的连乘。 解决分数连乘时,先找出具体的数量,一般是单位“1”,再 看比较量与单位“1”的关系,确定另一个单位“1”; 后根据第 三种量与单位“1”的关系计算。 注:可以通过画图的方法找到整体量,也就是单位“1”。 画图时,先找出单位“1”,再把单位“1”平均分成分母份数, 后把分子的份数表示出来。 如公牛有 30头,母牛的头数相当于公牛的 710,小牛的头 数相当于母牛的1621,小牛有多少头? 要求小牛的头数,就要知道母牛的量;母牛的头数又和 公牛的头数有关,先画一条线段,表示公牛的头数,再画一条 线段,表示母牛的头数,根据小牛和母牛的关系,画出表示小 牛的头数。 可得:小牛的头数=公牛头数× 710×1621。 应的量就是单位“1”对应的量,找 关键词“占”“是”“比”字后面的量是 单位“1”。 线段图是分析问题的 佳 方法,先确定第一个单位“1”,根据 第一个单位“1”确定第二个单位 “1”,再表示出未知量。线段图可 以直观表示出数量关系。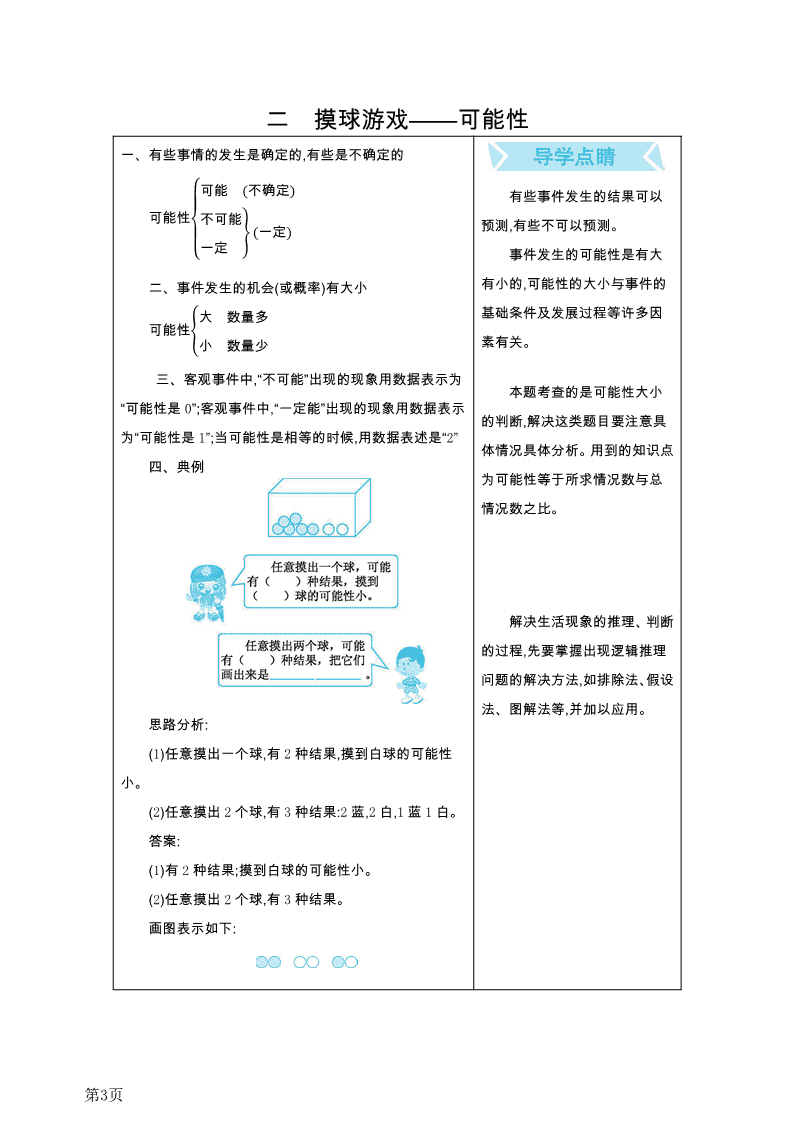 第2页 二 摸球游戏——可能性 一、有些事情的发生是确定的,有些是不确定的 可能性 可能 不确定 不可能 一定 一定 二、事件发生的机会(或概率)有大小 可能性 大 数量多 小 数量少 三、客观事件中,“不可能”出现的现象用数据表示为 “可能性是 0”;客观事件中,“一定能”出现的现象用数据表示 为“可能性是 1”;当可能性是相等的时候,用数据表述是“2” 四、典例 思路分析: (1)任意摸出一个球,有 2种结果,摸到白球的可能性 小。 (2)任意摸出 2个球,有 3种结果:2蓝,2白,1蓝 1白。 答案: (1)有 2种结果;摸到白球的可能性小。 (2)任意摸出 2个球,有 3种结果。 画图表示如下: 有些事件发生的结果可以 预测,有些不可以预测。 事件发生的可能性是有大 有小的,可能性的大小与事件的 基础条件及发展过程等许多因 素有关。 本题考查的是可能性大小 的判断,解决这类题目要注意具 体情况具体分析。用到的知识点 为可能性等于所求情况数与总 情况数之比。 解决生活现象的推理、判断 的过程,先要掌握出现逻辑推理 问题的解决方法,如排除法、假设 法、图解法等,并加以应用。 第3页 三 布艺兴趣小组——分数除法 一、分数除法 1. 分数除法的意义与整数除法的意义相同:已知两个 因数的积与其中一个因数,求另一个因数的运算。 2.一个数除以不为 0的数等于乘这个数的倒数。 3.比较商与被除数的大小。 除数小于 1,商大于被除数; 除数等于 1,商等于被除数; 除数大于 1,商小于被除数。 4.分数四则混合运算的运算顺序。 (1)先算乘除,再算加减,有括号的先算括号里面的,同 级运算从左到右; (2)分数连除运算可转化成连乘运算,能约分的先约分, 再计算; (3)在进行分数运算时,运用运算律可以使计算简便。 5.运用分数除法解决问题。 知识点一:“已知一个数的几分之几是多少,求这个数” 的问题的解法。 方程解法:找出单位“1”,设未知量为 x;找出题中的数量 关系式;列出方程。 算术法:(1)找出单位“1”; (2)找出已知量和已知量占单位“1”的几分之几; (3)列除法算式,即已知量÷已知量占单位“1”的几分之 几=单位“1”的量。 知识点二:“已知比一个数多(或少)几分之几的数是多 少,求这个数”的问题。 解题方法: (1)用方程解:把一个数设为未知量 x,根据题目中的数 量关系列出方程。 (2)算术法解:把一个数看作单位“1”,先计算出已知量占 单位“1”的几分之几, 已知量÷已知量占单位“1”的几分之几 =单位“1”的量 。 知识点一、二总结: (1)找单位“1”的关键词。 (2)已知单位“1”用乘法,未知单位“1”用除法。 知识点三:“已知一个数是另一个数的几分之几与这两 个数的和,求这两个数”的问题的解法。 解题方法: (1)用方程解:找到题中数量间的等量关系,设单位“1”的 量为 x,列出方程。 (2)用算术法解:找到题中的单位“1”,计算出两个数的和 占单位“1”的几分之几,两个数的和÷两个数的和占单位“1” 分数除法算式中出现小数 时要先化成分数、假分数,再计 算。 在进行分数运算时,可运用 运算律使计算简便。 解决分数除法问题的关键 是找准单位“1”,求单位“1”时用具 体的数除以它所占的分率,得出 的就是比较量。 基本的数量关系: 比较量÷标准量=分率。 用方程解决问题时,未知量 用 x代替,参与列式。 基本的数量关系: 分率对应的比较量÷分率= 标准量。 用方程解与用算术法解的 不同点:用方程解未知量参与列 式;用算术法解未知量不参与列 式。 基本的数量关系: 两个数的和÷(1+一个数是 另一个数的几分之几)=另一个 数 第4页 的几分之几=单位“1”的量。 知识点四:工程问题。 解决工程合修天数问题的方法: 一设:设这项工程为具体的数量或者单位“1”; 二列:根据“工作总量÷两队工作效率之和=工作时间” 列式; 三算:计算并验算写答。 二、典例讲解 例 1 学校组织爬山活动,小明上山平均每小时走 2.4 千米。原路返回,下山平均每小时走 3.6千米。小明上山、 下山的平均速度是多少? 思路分析:把路程看作单位“1 ” ,那么小明上山走了 1÷2.4= 512(时),下山走了 1÷3.5= 27(时)。根据平均速度的公 式:(上山路程+下山路程)÷(上山时间+下山时间)=平均速 度。 答案: (1+1)÷( 512+27)=16859 (千米) 答:小明上山、下山的平均速度是16859千米。 例 2 一批货物,第一次运走总数的15,第二次运走总数 的14,还剩下 143吨。这批货物有多少吨? 思路分析: 量、率的对应关系: 货物的总质量 “1”,第一次运走 的质量 15;第二次运走的质量 14;两次共运走的质量 15 + 14;还剩下 143吨 1- 15-14。 答案: 143÷(1-15-14) =143÷ 1120 =260(吨) 答:这批货物有 260吨。 解决工程问题,把工作总量 看作单位“1”,然后按照份数计算。 把上山和下山的总路程看 作单位“ 1 ” ,来回的路程就是 1+1=2,除以时间和就是平均速 度。 量、率对应关系的训练是解 较复杂分数应用题的重要环节。 根据应用题的已知条件发挥联 想,找出各种量、率间接的对应 关系,为正确解题铺平道路。 第5页 四 人体的奥秘——比 一、比值的意义 1. 比式中,比号(∶)前面的数叫作前项,比号后面的项 叫作后项,比号相当于除号。 2. 比的前项除以后项的商叫作比值,比值通常用分 数、小数和整数表示。 3. 求几个数的连比的方法。 如已知甲数与乙数的比是 5∶6,乙数与丙数的比是 8∶7,求甲、乙、丙三个数的连比。 解题时,可先把两个比排列成下面竖式的形式,再在两 个空位上填入左边或右边相邻的数(为了与比的项相区别, 用括号括起来), 后将每一竖行的两个数相乘,就得出了 甲、乙、丙这三个数的连比。如果这个连比中各项都含有 除 1以外的公因数,就用各项上的数除以公因数,直到它们 的 大公因数是 1为止,从而将这一连比化简。 甲 ∶ 乙 ∶ 丙 5 ∶ 6 8 ∶ 7 (5×8) ∶ 48 ∶ (7×6) 40 ∶ 48 ∶ 42 化简:20∶24∶21 4.比表示的是两个数的关系,可以用分数表示,写成分 数的形式,读作几比几。 12∶20读作:12比 20 比和比值的区别:比值是一个数,通常用分数表示,也可 以是整数、小数。 5.比的基本性质:比的前项和后项同时乘或除以相同 的数(0除外),比值不变。 6.化简比:化简之后结果还是一个比,不是一个数。 (1)化简整数比:找前项和后项的 大公因数,前项、后 项同时除以 大公因数,化成 简整数比。 (2)化简分数比:找前项和后项分母的 小公倍数,前 项、后项同时乘 小公倍数,再化简整数比。 (3)化简小数比:把小数转化成整数,再化简整数比。 (4)整数和整数的比:前、后项除以它们的 大公因数; (5)整数和分数的比:前、后项乘分母,再化简; (6)整数和小数的比:先把前、后项化成整数,再化简; (7)小数和分数的比:把小数化成分数,再按分数与分数 的比化简,或者把分数化成小数,再按小数和小数的比来化 简。 求比值:写成除号再计算,结果是一个数(或分数),相当 于商,不是比。 7.比和除法、分数的区别: 两个数相除又叫作两个数 的比。 比的后项不能为 0。 连比时,先求出相同量的两 个数的 小公倍数,再根据比的 基本性质计算出另外两种量的 数, 后把几种量的比化简成 简整数比。 比是一个式子,表示两个数 的关系,可以写成比,也可以写成 分数的形式。 运用比的基本性质可以化 简比。 根据比的前项和后项的特 点可以用不同的方法化简比。 有些比的单位不同,化简时 先统一单位。如 3米∶50厘米 =300厘米∶50厘米=6∶1。 第6页 除法 被除数 除号 (÷) 除数不 能为 0 商不变的性 质 除法是一种 运算 分数 分子 分数线 (——) 分母(不 能为 0) 分数的基本 性质 分数是一个 数 比 前项 比号 (∶) 后项(不 能为 0) 比的基本性 质 比表示两个 数的关系 用语言描述:比的前项相当于除法的被除数,相当于分 数的分子;比号相当于除号,相当于分数线;比的后项相当于 除法的除数,相当于分数的分母;比值相当于除法的商,相当 于分数的值。 二、按比分配 1.意义。 在农业生产和日常生活中,常常需要把一个数量按照 一定的比来进行分配。这种分配的方法通常叫作按比分 配。 2.解决按比分配应用题的方法: (1) 转化法: 分率 转化比 转化倍数 一般是把几个数的比转化成几个数分别占总数的几 分之几,再根据分数乘法的意义,求出这几个数。 (2) 把比化为分数,用分数来解答: 找出已知数量部分的份数; 求另外部分占已知数量的 几分之几;用分数乘法求出另一部分是多少。 (3) 用比的知识来解答: 求出部分之间的份数差; 求出每个部分占份数差的几 分之几;用分数乘法求出每个部分是多少。 3.典例讲解。 (1)甲、乙、丙三人合租一辆车运送同样的货物从 A地 到 B地,甲在全程的13处卸货,乙在行程刚好一半的地方卸 货,只有丙运到终点,共付运费 440元,他们该怎样分摊运费 比较合理? 思路分析: 此题要分配的总量是 440元,根据甲在全程的13处卸货, 乙在行程刚好一半的地方卸货,只有丙运到终点,可得出 甲、乙、丙三人合租这辆车需按照卸货地点的远近分摊运 费,运费的比是13∶12∶1,即 2∶3∶6,先求出总份数,再分别 求出甲、乙、丙分摊的运费占总运费的几分之几,进而分别 求得甲、乙、丙分摊的运费。 答案: 商不变性质:被除数和除数 同时乘或除以相同的数(0除外), 商不变。 分数的基本性质:分子和分 母同时乘或除以相同的数(0除 外),分数的大小不变。 方法:首先求出各部分占总 量的几分之几,然后求出总数的 几分之几是多少。 按比分配的方法解决实际 问题的一般步骤: 第一种类型的按比分配应 用题的解题步骤可以总结为(1) 求平均分得的总份数; (2)求每 个部分占总数量的几分之几;(3) 用分数乘法求出每部分是多少。 按比分配应用题: 题型 1:已知各种量,求比。 题型 2:已知比和其中一个 量,求其他量。 题型 3:已知比和总量,求每 一份的量。这是按比分配的基本 题型,也是小学阶段能解决的比 的基本问题。 看成份数时,要注意份数与 分量之间要对应准确。 第7页 甲、乙、丙分摊运费的比:13∶12∶1=2∶3∶6 总份数:2+3+6=11(份) 甲分摊的运费:440× 211=80(元) 乙分摊的运费:440× 311=120(元) 丙分摊的运费:440× 611=240(元) 答:他们应该按照卸货地点的远近分摊运费比较合理, 甲分摊的运费是 80元,乙分摊的运费是 120元,丙分摊的运 费是 240元。 第8页 五 完美的图形——圆 一、圆的定义 感知圆的特征:以前学过长方形、正方形、平行四边形、 梯形、三角形等,都是由线段围成的平面图形,而圆是由曲 线围成的一种平面图形。 二、圆的各部分名称 1.圆心:用圆规画出圆以后,针尖固定的一点就是圆心, 通常用字母 O表示。 2.半径:连接圆心到圆上任意一点的线段叫作半径。一 般用字母 r表示。 把圆规两脚分开,两脚之间的距离就是 圆的半径。 3.直径:通过圆心并且两端都在圆上的线段叫作直径。 一般用字母 d表示。 直径是一个圆内 长的线段。 三、圆的主要特征 1.在同圆或等圆内,有无数条半径,有无数条直径。所 有的半径都相等,所有的直径都相等。 2.在同圆或等圆内,直径的长度是半径的 2倍,半径的 长度是直径的12。用字母表示为 d=2r或 r=2。 3.如果一个图形沿着一条直线对折,两侧的图形能够 完全重合,这个图形是轴对称图形。圆是轴对称图形且有无 数条对称轴。 4. 画圆的方法: (1)用手指画圆。以大拇指为圆心,以食指与大拇指之 间的距离为半径,旋转一周所形成的图形就是圆。 (2)用线绳、图钉和笔画圆。用图钉固定线绳的一端作 圆心,将笔系在线绳的另一端,拉直绳子作半径,旋转线绳一 周所形成的图形就是圆。 (3)用圆规画圆。将圆规的一个针脚固定在本上作圆 心,用圆规两脚间的距离作半径,旋转圆规一周所形成的图 形就是圆。 (4)用物体的圆形面画圆。按住物体的圆形面,用笔在 物体的圆形面的圆周上画一圈,所形成的图形就是一个圆。 四、圆的周长的认识 1.围成圆的曲线的长叫作圆的周长。 2.周长与圆的直径有关,圆的直径越长,圆的周长就越 大。 五、 圆周率的意义及圆的周长公式 1.圆周率实验:在圆形纸片上做个记号,与直尺 0刻度 线对齐,在直尺上滚动一周,求出圆的周长。 2.发现一般规律,就是圆周长与它直径的比值是一个 固定数。 3.圆周率:任意一个圆的周长与它的直径的比值是一 个固定的数,我们把它叫作圆周率。用字母π(pài)表示。 4.一个圆的周长总是它直径的 3倍多一些,这个比值 圆与其他平面图形不同的, 圆是曲线图形,其他图形是线段 图形。 直径和半径的关系只能在 同圆和等圆中。 用字母表示:d=2r 不能说直径是圆的对称轴。 因为对称轴是一条直线。 圆心决定圆的位置,半径决 定圆的大小。 半径越大,画出的圆越大。 我们通常选用圆规画圆,既 便捷又准确。 可以用绳测法或滚动法找 出圆的直径和周长的关系。 世界上第一个把圆周率算 出来的人是我国的数学家祖冲 之。 第9页 是一个固定的数。圆周率π是一个无限不循环小数。在计 算时,一般取π ≈ 3.14。 5.圆的周长公式: C= πd → d = C ÷π或 C=2π r → r = C ÷ 2π。 6.区分周长的一半和半圆的周长: (1)周长的一半:等于圆的周长÷2。计算方法:2π r ÷ 2,即 π r。 (2)半圆的周长:等于圆的周长的一半加直径。 计算 方法:πr+2r,即 5.14 r 。 7.正方形里 大的圆与正方形的关系。 两者联系:正方形的边长=圆的直径,圆的面积=78.5% 正方形的面积。 8.画法: (1)在正方形里画 大的圆。 ①画出正方形的两条对角线;②以对角线的交点为圆 心,以边长为直径画圆。 (2)长方形里 大的圆。 两者联系:宽=直径 画法: ①画出长方形的两条对角线;②以对角线的交点为圆 心,以宽为直径画圆。 五、常用的 3.14的倍数 3.14×2=6.28 3.14×3=9.42 3.14×4=12.56 3.14×5=15.7 3.14×6=18.84 3.14×7=21.98 3.14×8=25.12 3.14×9=28.26 3.14×12=37.68 3.14×14=43.96 3.14×16=50.24 3.14×18=56.52 3.14×24=75.36 3.14×25=78.5 3.14×36=113.04 3.14×49=153.86 3.14×64=200.96 3.14×81=254.34 六、圆的面积公式 把圆拼成近似的长方形,只是形状改变了,图形的大小 并没有发生变化,因此圆的面积=拼成的近似长方形的面 积。 圆的面积推导: 圆可以切拼成近似的长方形,长方形的面积与圆的面 积相等(即 S 长方形=S 圆);长方形的宽是圆的半径(即 b=r);长 在判断时,圆周长与它直径 的比值是π倍,而不是 3.14倍。 一个图形的周长就是围成 这个图形一周的长,具体情况要 具体分析。 在长方形或正方形内画 大圆,关键是以对角线的交点为 圆心,以到正方形的边长或长方 形宽的距离为半径。 记忆常用 3.14的倍数,可以 使平时的计算快捷、正确。 圆的面积与以它的半径为 边长的正方形的面积的关系:以 正方形的边长为半径画的圆,正 方形的面积实际就是这个圆半 径的平方,因此得出“圆的面积是 它半径平方的 3倍多一些”圆的 面积大约等于半径×半径×3。 注意:切拼后的长方形的周 长比圆的周长多了两条半径。C 长方形=2πr+2r =C 圆+d。 周长相等的平面图形中,圆 的面积 大;面积相等的平面图 形中,圆的周长 短。 要求圆的面积只要知道圆 的半径或者知道圆的半径的平 方。 第10页 方形的长是圆周长的一半(即 a=C÷2=πr)。 S 长方形=a × b S 圆 =πr×r =πr2 所以,S 圆 =πr2。 七、圆环的意义及面积的计算 1.圆环的意义:以同一点为圆心,半径不相等的两个圆 组成的图形,两圆之间的部分就是圆环。 2.圆环中半径较大的圆叫作外圆,半径较小的圆叫作 内圆。外圆半径与内圆半径的差叫作环宽,两圆中间的部分 的大小叫作圆环的面积。 3.外圆的半径=内圆半径+1个环宽;外圆的直径=内圆 直径+2个环宽。 4.求圆环的面积一般是用外圆的面积减去内圆的面 积,还可以利用乘法分配律进行简便计算。S 圆环=S 外圆-S 内 圆=πR2-πr2= π(R2-r2)。 5.几个直径和为 n的圆的周长=直径为 n的圆的周长 (如图)。 几个直径和为 n的圆的面积<直径为 n的圆的面积。 八、扇形的认识 1.扇形是由“一条弧”和“经过这条弧两端的两条半径” 所围成的图形。 扇形是所在圆上的一部分,∠AOB是圆心角;扇形是由 两条半径和圆上一段曲线围成的。 2.扇形与三角形的区别。 扇形是由两条半径和一条弧围成的图形;三角形是由 三条线段围成的图形。尽管有的图形的两条边也是圆的半 径,但是第三条边不是弧,而是线段,这样的图形不能称为扇 形,它是三角形。弧是圆的一部分,是曲线,而线段是直线的 一部分。 圆环的意义: 两个同心圆形成一个圆环。 设小圆和大圆(或内圆和外 圆)的半径和直径分别为 r和 R。 (R﹥r) 同样大小的外圆,内圆越小, 圆环的面积越大。 半圆环的面积=它所在的圆 环面积的一半。 单独一个圆,半径(直径)越 大,周长就越大,面积也越大;如 果两个圆的半径相等,那么它们 的周长就相等,面积也相等。 在同一个圆中,扇形的大小 与这个扇形的圆心角的大小有 关,圆心角大的扇形大,圆心角小 的扇形小。 在同圆或等圆中,圆心角越 大,扇形越大;反之,圆心角越小, 扇形就越小。 第11页 第12页 六 中国的世界遗产——分数四则混合运算 分数四则混合运算 1.运算顺序: (1) 同级运算,从左到右。 小技巧:可以随便调换位置,但要连同数字前面的运算 符号一起调换。 对于二级运算,遇“÷”先变“ ×”,除数变倒数,“一线到底” 约分到 简分数。所谓“一线到底”,在加减法中,先通分再计 算;在乘除法中,遇“除” 变“乘”,一次性约分,约到不能再约分 为主。 (2)异级运算,先乘除,后加减。 (3)有括号,要先算小括号里面的,再算中括号里面的, 后算中括号外面的。 2.简便运算。 在分数四则混合运算中,可以同时运用整数运算律,使 计算简便。 加法交换律:a+b=b+a 加法结合律:(a+b)+c=a+(b+c) 乘法交换律:ab=ba 乘法结合律:(ab)c=a(bc) 乘法分配律:a(b+c)=ac+bc 3.审题技巧。 分数乘法的意义在文字题中是个“陷阱”,如比 5吨多45 是多少吨? 这道题中的“比 5吨多45”不是“差比”,而是“倍比”,一不小 心就会列成 5+ 45,正确的列式为 5+5× 45。 4.用方程解文字题是一种顺向思维的列式,在解决问 题过程中可以把未知数用 x代替,找出等量关系,然后把 x 作为已知量参与运算, 终得到等式求出未知量。 典例讲解 修一条路,第一天修了全长的13,第二天修了全长的14,第 二天比第一天多修了 300米,这条路长多少米? 思路分析: 根据“第一天比第二天多修了 300米”可以列出等量关 系式,即“第一天修的长度-第二天修的长度=300米”把全长 看作单位“1”,列出方程计算。 答案: 在第一级运算中,某两分数 直接相加或相减得整数的情况 除外。 除了学过的运算,还可以用 下面的方法简算。 减法的性质: a-b-c=a-(b+c) 或 a-(b+c) =a-b-c 除法的性质: a÷b÷c=a÷(b×c)或 a÷(b×c)= a÷b÷c 正确区分分数和分率,才能 解答正确。 首先判断单位“1”的量:知道 单位“1”的量(用乘法),不知道单 位“1”的量(用除法),为确定解题 方法奠定基础;然后会把“比”字句 转化成“是”字句; 后能将省略式 的分率句换说成比较详细的句 子的能力。 未知数的设法: 在分数应用题中,我们设单 位“1”为 x; 在有比的问题中,设 1 份数为 x;在有和的问题中,设其 中任意一个为 x都可以,比如说 两个班共有 50人,设其中一个班 有 x人。 第13页 解:设这条路长 x米。13x-14x=300112x=300 x=300÷ 112 x=3600 答:这条路长 3600米。 5.分数应用题主要讨论的是以下三者之间的关系: (1)分率:表示一个数是另一个数的几分之几,这几分之 几通常称为分率。 (2)标准量:解答分数应用题时,通常把题目中作为单位 “1”的那个数,称为标准量。(也叫单位“1”的数量) (3)比较量:解答分数应用题时,通常把题目中同标准量 比较的那个数,称为比较量。(也叫分率对应的数量) 6.分数应用题的分类。 (1)求一个数的几分之几是多少。(解这类应用题用乘 法) 这类问题特点是已知一个看作单位“1”的数,求它的几 分之几是多少,它反映的是整体与部分之间关系的应用题。 (2)已知一个数的几分之几是多少,求这个数。(解这类 应用题用除法) 这类问题特点是已知一个数的几分之几是多少的数 量,求单位“1”的量。 (3)求一个数是另一个数的几分之几。(解这类应用题 用除法) 这类问题特点是已知两个数量,比较它们之间的倍数 关系。 7.稍复杂的分数问题: (1)已知甲数,乙数比甲数的几分之几多(或少)多少,求 乙数。 (2)已知总数,甲是总数的几分之几,乙是总数的几分之 几,求甲、乙的和或者差。(两种关系式,两种思路) (3)已知总数,其中甲是总数的几分之几,求剩下的。(两 种关系式,两种思路) (4)已知甲数和乙数比甲数多(或少)几分之几,求乙数。 (两种关系式,两种思路) (5)已知一个数的几分之几是多少,求这个数,既可以用 除法计算,也可以列方程解答。 解决分数应用题时: 先要弄清两个概念:带单位 的分数和不带单位的分数。 带 单位的分数,如34吨,叫数量,表示 一个物体的具体的数量。不带单 位的分数,如34,叫分率,它表示一 个数的几分之几。 应用题解题思路: 第一步:确定单位“1”。 找 单位“1”的方法:找到题中不带单 位的分数的那句话,“谁”的几分之 几,那个“谁”就是单位“1”。第二步: 确定乘除法 。(1)题中直接或间 接告诉单位“1”的或可直接算出 单位“1”的,用乘法;(2)题中单位“1” 是未知的,用除法。第三步:列式。 第四步:检查 。 第14页 七 体检中的百分数——百分数(一) 一、百分数的认识 1.百分数的意义。 (1)表示一个数是另一个数的百分之几。 (2)百分数是指两个数的比,因此也叫百分率或百分 比。 (3)百分数通常不写成分数形式,而采用百分号“%”,百分 数后面不能带单位名称。 2.百分数和分数的主要联系与区别。 (1)联系:都可以表示两个量的倍比关系。 (2)区别。 ①意义不同:百分数只表示两个数的倍比关系,不能表 示具体的数量,所以不能带单位;分数既可以表示具体的 数,又可以表示两个数的关系,表示具体数时可以带单位。 ②百分数的分子可以是整数,也可以是小数,如 2.5%; 而分数的分子不能是小数,只能是除 0以外的自然数。 ③百分数的读法和分数的读法大体相同,也是先读分 母,后读分子,但要注意读百分数的分母时,不能读成一百 分之几,而只能读作“百分之几”。 3.百分数的写法。 通常不写成分数形式,而在原来分子后面加上“%”来表 示。如 5%,20%。 4.百分数、分数、小数的互化。 (1)小数化成百分数:把小数点向右移动两位,同时在后 面添上百分号。 如 0.23、5、0.026 三个数字化成百分数是 23%、 500%、2.6%。 (2)百分数化成小数:把小数点向左移动两位,同时去掉 百分号。 如 20%,56%,3.7%三个数字化成小数是 0.2、0.56、 0.037。 (3)百分数化成分数:先把百分数化成分数,再把百分数 改写成分母是 100的分数,能约分要约成 简分数。 如 25%、40%,化成分数是 25%= 25100=14、40%= 40100=25。 (4)分数化成百分数。 ① 用分数的基本性质,把分数的分母扩大或缩小成 分母是 100的分数,再写成百分数形式。 如25化成百分数形式:25=2×205×20= 40100=40%。 ② 先把分数化成小数(除不尽时,通常保留三位小数), 再把小数化成百分数。 百分数表示两个数的关系, 不表示一个具体的数,所以不能 有单位。 百分号前面的数相当于分 数的分子,百分号后面的数相当 于分数的分母。 百分数的分子部分可以是 小数、整数,可以大于 100,小于 100或等于 100。 在进行分数、小数和百分数 互化的过程中,不能改变原来数 的大小。 比较百分数、分数和小数的 大小时,要先将这些数转化成相 同的数,再进行比较。 后结果要 写成原数进行比较。 当分数的分子除以分母不 能得到有限小数时,化成百分数 就是一个近似数。 如发芽率、出勤率、合格率、 成活率、中奖率、命中率、出生 率、死亡 率、优秀率、及格率、 第15页 如34化成百分数形式:34=3÷4=0.75=75%。 二、常用百分率的计算 合格率= 合格产品数 产品总数 ×100%;成活率= 成活的棵数 总棵数 ×100%; 烘干率= 烘干后的质量 烘干前的质量 ×100%;发芽率= 发芽种子数 种子总数 ×100%; 达标率= 达标学生人数 学生总人数 ×100%; 含水率= 烘干前的质量‐烘干后的质量 烘干前的质量 ×100%。 三、解决百分数问题的方法 1.求一个数是另一个数的百分之几。 计算方法:把另一个数看作单位“1”,用一个数除以单位 “1”。 即一个数÷另一个数; 后的结果化成百分数。 2.“求数 A比数 B多(或少)百分之几?”的实际问题。 已知条件:数 A、数 B; 求:两数差的百分数; 解题方法:(大数-小数)÷单位“1”。 3.“数 A比数 B多(或少)百分之几,求数 A是多少?”的实 际问题。 已知条件:数 B、 两数和(差)的百分数。 求:数 A(非单位“1”) 解题方法:数 B×(1+百分数)——两数和的方法 数 B×(1-百分数)——两数差的方法 4.“数 A比数 B多(或少)百分之几,求数 B是多少?”的实 际问题。 已知条件:数 A、两数和(差)的百分数 求:数 B(单位“1”) 解题方法: 数 A÷(1+百分数)——两数和的方法 数 A÷(1-百分数)——两数差的方法 出油率、出错率、入学率、含盐 率、含糖率、增长率、近视率、 收视率等 大不会超过 100%。增 长率可以大于 100%。 实际生活中,人们常用增加 了百分之几、减少了百分之几、 节约了百分之几等来表示增加 或减少的幅度。 口诀:“一减一 除”。(两数的差÷单位“1”=百分 之几) 第16页